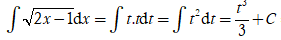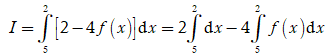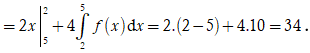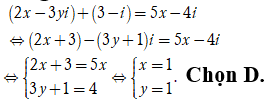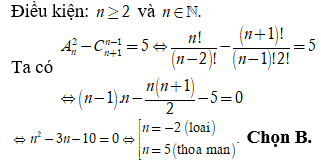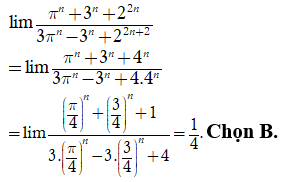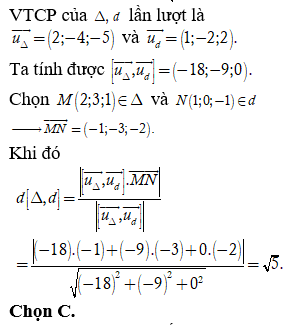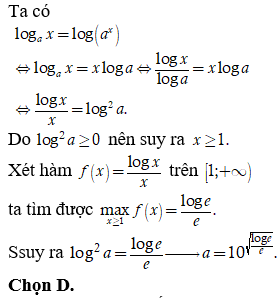Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết(Đề 6)
-
22325 lượt thi
-
50 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
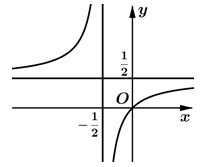
Các chi tiết đồ thị hàm số có TCĐ: ![]() đều giống nhau
đều giống nhau
Chỉ có chi tiết đồ thị hàm số đi qua gốc tọa độ là phù hợp cho đáp án C. Chọn C.
Câu 2:
Hàm số đồng biến trên khoảng nào sau đây ?
Ta có ![]()
Khi đó  Hàm số đồng biến trên
Hàm số đồng biến trên
Chọn A.
Câu 3:
Đồ thị của hàm số có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB ?
![]()
![]()
![]()
Tọa độ các điểm cực trị là A(-1;6) và B(3;-26)
=> đường thẳng đi qua hai điểm cực trị là AB: 8x+2y+2 = 0.
Kiểm tra ta được ![]()
Chọn A.
Câu 4:
Cho hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
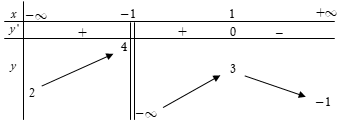
Khẳng định nào dưới đây là sai?
Dựa vào bảng biến thiên nhận thấy hàm số đồng biến trên các khoảng và (-1;1)
Vì vậy khẳng đinh C là sai. Chọn C.
Câu 5:
Cho các số thực và thỏa mãn . Giá trị của bằng
Nhận thấy các đáp án đều có tích xy nên ta sẽ tính tích này.
Ta có ![]()
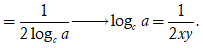
Chọn C.
Câu 7:
Phương trình có bao nhiêu nghiệm âm?
Phương trình tương đương với ![]()
Đặt ![]() Phương trình trở thành
Phương trình trở thành 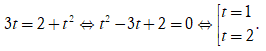
● Với t=1, ta được ![]()
● Với t=2, ta được ![]()
Vậy phương trình có duy nhất một nghiệm âm ![]()
Chọn B.
Câu 8:
Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm thực phân biệt.
Đặt ![]() Phương trình trở thành
Phương trình trở thành ![]()
Nhận xét: Với mỗi nghiệm ta tìm được tương ứng hai nghiệm x
Xét hàm ![]()
Ta có ![]()
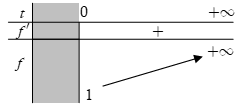
Dựa vào bảng biên thiên, ta thấy yêu cầu bài toán ![]()
Chọn A
Phương pháp hình học. Nhận thấy phương trình là phương trình hoành độ giao điểm của đồ thị hàm số ![]() và nửa đường tròn
và nửa đường tròn ![]() (phần phía trên trục hoành) như hình vẽ. Dựa vào hình vẽ ta thấy để hai đường này cắt nhau tại hai điểm phân biệt khi
(phần phía trên trục hoành) như hình vẽ. Dựa vào hình vẽ ta thấy để hai đường này cắt nhau tại hai điểm phân biệt khi ![]()
Câu 9:
Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất . Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Tính số tiền tối thiểu x triệu đồng ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng.
Áp dụng công thức lãi kép ![]() số tiền gửi vào lần đầu tiên, r = 6,5% là lãi suất mỗi năm, n = 3 năm.
số tiền gửi vào lần đầu tiên, r = 6,5% là lãi suất mỗi năm, n = 3 năm.
Suy ra số tiền người đó nhận được (cả vốn ban đầu và lãi) là: ![]()
Suy ra số tiền lãi người đó nhận được là: ![]()
Theo đề, ta có 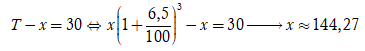 triệu đồng.
triệu đồng.
Chọn B.
Câu 12:
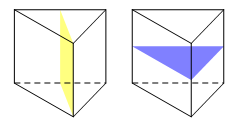
Tính diện tích hình phẳng được tô đậm ở hình bên.
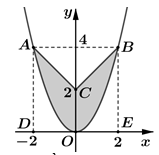
Áp dụng công thức tính nhanh, ta có diện tích miền khép kín giới hạn bởi Parabol và đường ![]()
Diện tích tam giác ABC là ![]()
Suy ra diện tích phần tô đậm ![]()
Chọn B.
Câu 13:
Thể tích V của khối tròn xoay khi cho hình phẳng H giới hạn bởi các đường và quay quanh trục Ox được xác định bởi công thức nào sau đây?

Phương trình hoành độ giao điểm: ![]()
Vì đồ thị hàm số đối xứng với đồ thị hàm số qua trục hoành nên thể tích khối tròn xoay cần tính bằng thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đường ![]() quay quanh trục Ox. Vậy công thức tính thể tích là
quay quanh trục Ox. Vậy công thức tính thể tích là
Chọn C.
Câu 15:
Trong hình vẽ bên, điểm A biểu diễn số phức . Tìm điểm biểu diễn số phức z.

Dựa vào hình vẽ, ta có A(1;3)![]()
Vậy điểm biểu diễn số phức z là điểm E(2;2). Chọn D.
Câu 18:
Xét các số phức z thỏa mãn là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng?
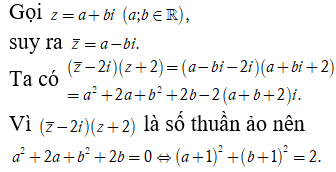
Vậy tập hợp tất cả các điểm biễu diễn số phức z là một đường tròn có bán kính bằng . Chọn B.
Câu 20:
Cho khai triển với . Hỏi có bao nhiêu giá trị sao cho tồn tại k thỏa mãn
![]()
![]()
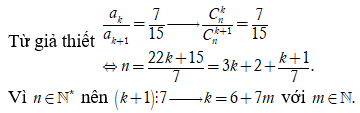
Khi đó ![]()
=> có 91 số. Chọn C.
Câu 21:
Sau khi kết thúc một trận đấu đầy kịch tính (trận lượt về giữa VIỆT NAM và PHILIPPINES), đội bóng của hàng triệu người yêu mến đã dành chiến thắng thuyết phục 2-1. Một buổi liên hoan nhẹ cho các cầu thủ, ban huấn luyện, quan chức,… được tổ chức nhanh chóng. Để tiện việc ghi hình, phỏng vấn,… Ban tổ chức dự định sắp xếp hai cầu thủ ghi bàn vào trong cùng một bàn tròn có 10 chỗ ngồi (các chỗ ngồi được đánh số thứ tự) và ngồi đối diện nhau (ví dụ như hai cầu thủ ngồi ở vị trí ghế số 5 và ghế số 10). Hỏi rằng có bao nhiêu cách sắp xếp?
Gọi tên hai cầu thủ ghi bàn là A và B.
Cứ mỗi vị trí ngồi của A có đúng một cách sắp xếp A-B. Vì A có 10 vị trí ngồi nên có 10 cách sắp xếp. Chọn A.
Chú ý. Đề chỉ quan tâm đến hai cầu thủ ghi bàn và cách xếp hai cầu thủ này ngồi đối diện trong bàn tròn có 10 chỗ ngồi.
Câu 23:
Một cửa hàng ngày đầu chỉ bán được 5 sản phẩm, nhưng do quảng cáo hiệu quả và chất lượng sản phẩm tốt nên những ngày sau số lượng sản phầm bán ra đều tăng gấp đôi so với ngày trước đó. Số ngày ít nhất để cửa hàng đó bán hết 1200 sản phẩm là?
Số sản phẩm bán được ở ngày 1,2,3,.... lập thành cấp số nhân với , q = 2. Theo giả thiết ta có:
![]() Tới đây ta dùng máy tính cầm tay để tìm n hoặc thay n lần lượt bằng các giá trị trong các đáp án và chọn giá trị n nhỏ nhất thỏa mãn. Chọn B.
Tới đây ta dùng máy tính cầm tay để tìm n hoặc thay n lần lượt bằng các giá trị trong các đáp án và chọn giá trị n nhỏ nhất thỏa mãn. Chọn B.
Câu 25:
Cho hàm số có đồ thị (C). Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng . Gọi h là khoảng cách giữa hai tiếp tuyến đó. Khẳng định nào sau đây đúng?
Từ giả thiết suy ra tiếp tuyến có hệ số góc bằng -1
Hai tiếp điểm có hoành độ là nghiệm của phương trình
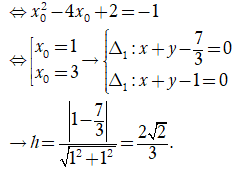
Chọn C.
Câu 26:
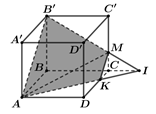
Cho tứ diện ABCD, G là trọng tâm của tam giác ABD và M là điểm trên cạnh BC sao cho . Đường thẳng MG song song với mặt phẳng
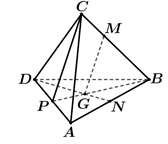
Gọi P là trung điểm của AD.
Vì G là trọng tâm tam giác BCD nên 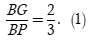
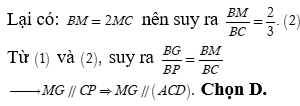
Câu 27:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABC) và . Gọi là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?
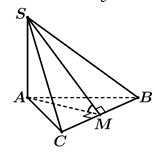
Gọi M là trung điểm BC, suy ra
Tam giác ABC đều cạnh a suy ra trung tuyến ![]()
Tam giác vuông SAM có ![]()
Chọn D.
Câu 28:
Cho hình lập phương có cạnh bằng 1. Khoảng cách từ điểm A đến mặt phẳng (BDA') bằng

Chọn C.
Câu 29:
Cho hình lập phương ABCD.A'B'C'D'. Gọi là góc giữa AC' và mặt phẳng . Chọn khẳng định đúng trong các khẳng định sau?
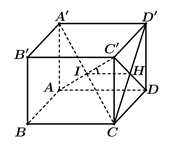
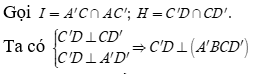
=> IH là hình chiếu vuông góc của IC' trên mặt phẳng
Do đó ![]()
Trong tam giác vuông C'HI, có 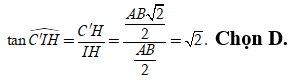
Câu 30:
Cho hình lăng trụ đứng có đáy là tam giác vuông và là trung điểm của BC. Khoảng cách của hai đường thẳng AM và B'C bằng
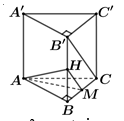
Lời giải.
Gọi H là trung điểm của BB' => HM//B'C
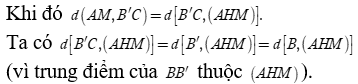
Theo đề, ABC.A'B'C' là lăng trụ đứng và ABC vuông tại B (vì AB = BC = a)
=> tứ diện BAHM có BA, BH, BM đôi một vuông góc nhau. Khi đó
Câu 31:
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
Hình lăng trụ tam giác đều có mặt phẳng đối xứng (hình vẽ bên dưới).
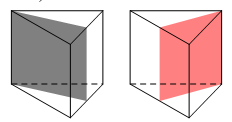
Chọn D.
Câu 32:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD) cạnh . Thể tích của khối chóp S.ABCD bằng
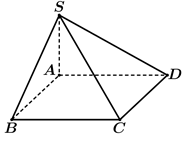
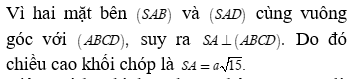
Diện tích hình chữ nhật ABCD là 
Chọn C.
Câu 33:
Cho hình lập phương có cạnh 4cm. Mặt cầu tiếp xúc với cạnh của hình lập phương đó có diện tích xung quanh là
Gọi O là tâm của hình lập phương và AB là một cạnh đáy của hình lập phương. Khi đó bán kính mặt cầu là
![]() Vậy diện tích mặt cầu là
Vậy diện tích mặt cầu là ![]()
Chọn C.
Câu 34:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và . Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD bằng
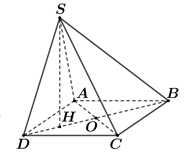
Xác định được ![]()
Tính được ![]()
![]()
Suy ra tam giác SBD vuông tại S. Vậy các đỉnh S, A, C cùng nhìn xuống BD dưới một góc vuông nên ![]()
Chọn B.
Câu 35:
Trong không gian với hệ tọa độ , cho tam giác ABC có đỉnh và trọng tâm Tìm tọa độ các đỉnh A, B của tam giác ABC, biết A thuộc mặt phẳng (Oxy) và điểm B thuộc trục cao.

Chọn B.
Câu 36:
Trong không gian với hệ tọa độ Oxyz cho ba điểm . Tập hợp các điểm thỏa là mặt cầu có bán kính
Ta có
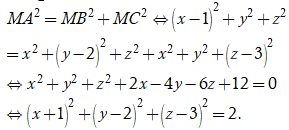
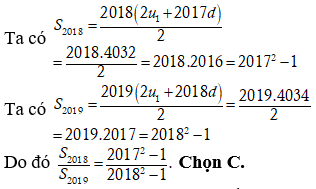
Suy ra tập hợp các điểm M(x,y,z) thỏa mãn là mặt cầu có bán kính . Chọn A.
Câu 37:
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) cắt trục Oz tại điểm có cao độ bằng 2 và song song với mặt phẳng (Oxy). Phương trình cửa mặt phẳng (P) là
![]()
![]()
Mặt phẳng cần tìm (P) đi qua M(0;0;2) và nhận làm một VTPT nên có phương trình (P): z - 2 = 0
Chọn A.
Câu 38:
Trong không gian với hệ tọa độ Oxyz tìm trên trục Oz điểm M cách đều điểm và mặt phẳng
Giả sử ![]() là điểm cần tìm.
là điểm cần tìm.
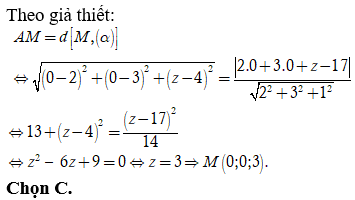
Câu 39:
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng và . Xác định góc giữa hai đường thẳng và
Đường thẳng có một VTCP ![]()
có một VTCP ![]()
Chọn A.
Câu 41:
Cho hàm số có đạo hàm với mọi . Hỏi số thực nào dưới đây thuộc khoảng đồng biến của hàm số ?
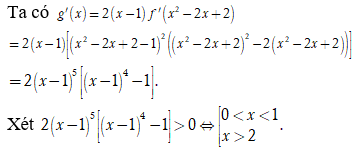
Suy ra hàm số đồng biến trên các khoảng ![]()
Vậy số 3 thuộc khoảng đồng biến của hàm số g(x)
Chọn B.
Câu 42:
Cho hàm số . Đồ thị của hàm số như hình vẽ bên. Hỏi hàm số có bao nhiêu điểm cực trị?
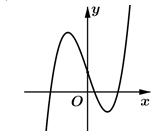
Từ đồ thị hàm số f'(x) ta thấy f'(x) cắt trục hoành tại 2 điểm có hoành độ dương (và 1 điểm có hoành độ âm)
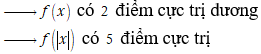
![]() có 5 điểm cực trị với mọi m (vì tịnh tiến lên trên hay xuống dưới không ảnh hưởng đến số điểm cực trị của hàm số). Chọn C.
có 5 điểm cực trị với mọi m (vì tịnh tiến lên trên hay xuống dưới không ảnh hưởng đến số điểm cực trị của hàm số). Chọn C.
Câu 43:
Cho hàm số bậc ba có bảng biến thiên như hình vẽ. Đồ thị hàm số có bao nhiêu đường tiệm cận đứng?

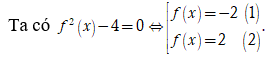
Dựa vào bảng biến thiên, ta thấy
• (1) có nghiệm duy nhất x = a < 0
![]() là hàm bậc hai và h(x) = 0 vô nghiệm.
là hàm bậc hai và h(x) = 0 vô nghiệm.
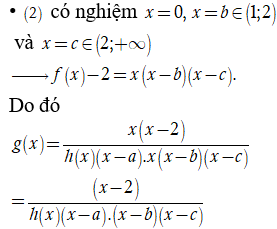
=> đồ thị hàm số g(x) có 3 đường tiệm cận đứng. Chọn C
Câu 44:
Cho phương trình . Có tất cả bao nhiêu giá trị nguyên của m để phương trình có bốn nghiệm thực phân biệt?
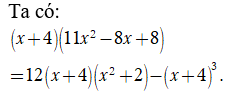
Khi đó phương trình đã cho trở thành

Để phương trình đã cho có bốn nghiệm thực phân biệt phương trình (2) có hai nghiệm phân biệt thuộc (1;3)
![]() có 4 giá trị nguyên m thỏa. Chọn A.
có 4 giá trị nguyên m thỏa. Chọn A.
Câu 46:
Cho hàm số có đạo hàm liên tục trên . Hình bên là đồ thị của hàm số . Đặt . Khẳng định nào sau đây đúng?
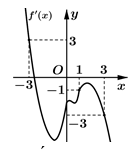
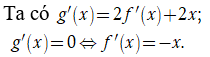
Ta thấy đường thẳng y=-x cắt đồ thị hàm số y=f'(x) tại các điểm có hoành độ -3;1;3
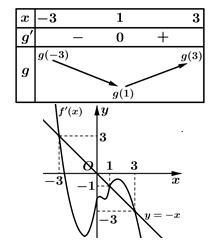
Dựa vào bảng biến thiên, suy ra ![]()
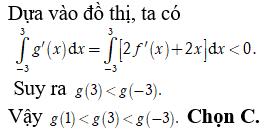
Câu 47:
Cho hàm số có đồ thị như hình bên. Hỏi có bao nhiêu điểm trên đường tròn lượng giác biểu diễn nghiệm của phương trình ?
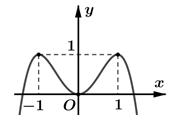
Dựa vào đồ thị ta thấy khi ![]()
Do đó nếu đặt t = cos2x thì ![]()
Dựa vào đô thị, ta có 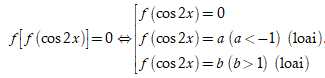
Phương trình f(cos2x)=0 ![]()
Vậy phương trình đã cho có 4 điểm biểu diễn nghiệm trên đường tròn lượng giác. Chọn C.
Câu 48:
Trong ngăn kéo của An có 5 đôi tất, mỗi đôi một màu khác nhau. Ngày thứ Hai (ngày đầu tuần), An chọn ngẫu nhiên 2 chiếc từ 10 chiếc tất trong ngăn kéo. Thứ Ba, An chọn ngẫu nhiên tiếp 2 chiếc tất từ 8 chiếc tất còn lại. Thứ Tư, An chọn ngẫu nhiên tiếp 2 chiếc tất từ 6 chiếc tất còn lại. Xác suất để Thứ Tư là ngày đầu tiên An chọn đúng 2 chiếc tất cùng một đôi bằng
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố ngày thứ Tư mới lấy được đôi tất .
• Ngày thứ Hai không chọn được 1 đôi tất nghĩa là 2 chiếc khác đôi.
Do đó có ![]()
• Ngày thứ Ba còn 8 chiếc tất trong đó có 6 chiếc lập thành 3 đôi và 2 chiếc tất không tạo được đôi.
… TH1: Nếu lấy hai chiếc tất thừa thì ngày thứ Tư có 3 cách chọn được một đôi.
… TH2: Nếu lấy 1 trong 2 chiếc tất thừa thì ngày thứ Ba có cách và ngày thứ Tư có 2 cách.
… TH3: Nếu không lấy chiếc này trong hai chiếc tất thừa thì ngày thứ Ba có cách và ngày thứ Tư có 1 cách.
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính là 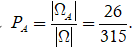
Chọn B.
Câu 50:
Trong không gian với hệ tọa độ Oxyz cho hai điểm và . Gọi là mặt phẳng chứa A và trục Oy; là mặt phẳng chứa B và trục Oz. Biết rằng và cắt nhau theo giao tuyến là đường thẳng có vectơ chỉ phương . Tính độ dài đoạn thẳng AB

Mặt phẳng chứa A và trục Oy nên có một VTPT là ![]()
Đường thẳng là giao tuyến của và nên có VTCP ![]()
Theo giả thiết, ta có cùng phương với ![]()
Suy ra 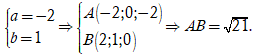
Chọn C.