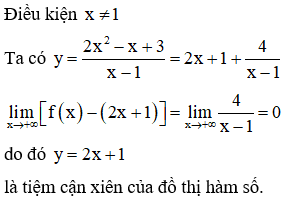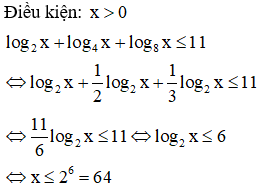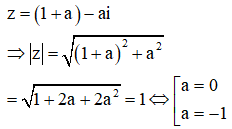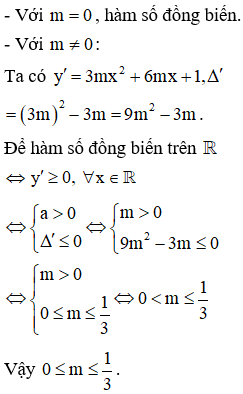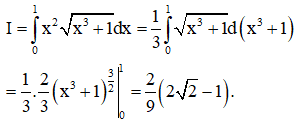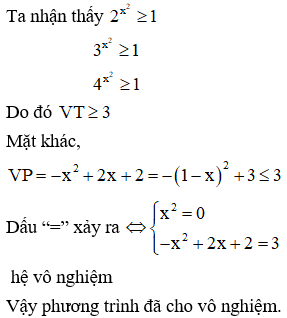Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết(Đề 20)
-
22232 lượt thi
-
51 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Trong không gian tọa độ Oxyz, cho ba điểm . Viết phương trình mặt cầu có tâm là gốc tọa độ và tiếp xúc với mặt phẳng (ABC).
Đáp án C.
Phương trình đoạn chắn của mặt phẳng (ABC):

Câu 2:
Trong không gian tọa độ Oxyz, cho mặt cầu và . Tìm các giá trị của m để tiếp xúc với .
Đáp án B.

Câu 4:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số liên tục trên , trục hoành và hai đường thẳng được tính theo công thức nào sau đây?
Đáp án D.
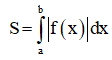
Câu 6:
Hàm số có giá trị cực đại là
Đáp án B.
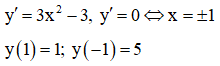
Do đó giá trị cực đại của hàm số là y(-1)=5.
Câu 8:
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường quanh trục Ox là
Đáp án B.
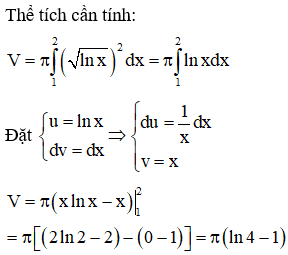
Câu 9:
Cho hàm số và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ là
Đáp án D
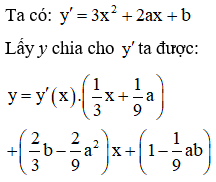
Do đó phương trình đường thẳng đi qua hai điểm cực trị là
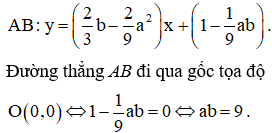
Câu 10:
Cho hàm số và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ là
Đáp án D
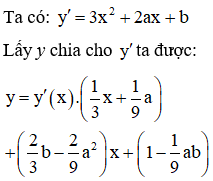
Do đó phương trình đường thẳng đi qua hai điểm cực trị là
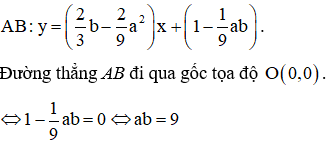
Câu 13:
Hình hộp chữ nhật có độ dài ba cạnh xuất phát từ một đỉnh lần lượt là 3, 4, 5. Thể tích của hình hộp đó là
Đáp án C
Thể tích hình hộp đó là V = 3.4.5=60
Câu 14:
Khoảng nghịch biến của hàm số là
Đáp án D
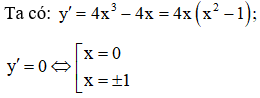
Bảng biến thiên:
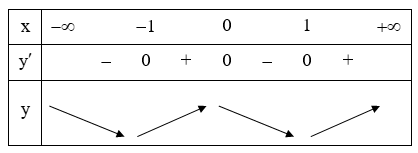
Hàm số nghịch biến trên các khoảng
Câu 15:
Trong không gian với hệ tọa độ Oxyz, cho điểm . Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy, Oz. Mặt phẳng nào sau đây song song với mặt phẳng .
Đáp án A.

Câu 16:
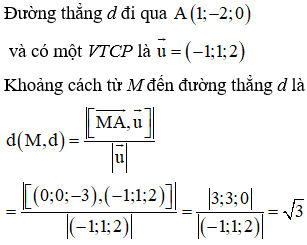
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và điểm . Tìm khoảng cách từ M đến đường thẳng d.
Đáp án D.
Câu 19:
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số không có tiệm cận đứng.
Đáp án A.
Đồ thị hàm số không có tiệm cận đứng
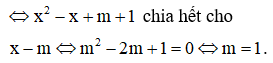
Câu 21:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và đường thẳng . Gọi là góc giữa hai đường thẳng và . Tính xấp xỉ .
Đáp án B.

Câu 22:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm . Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Đáp án C.
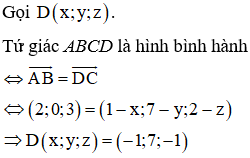
Câu 23:
Người ta xếp các hình vuông kề với nhau như trong hình vẽ dưới đây, mỗi hình vuông có độ dài cạnh bằng nửa độ dài cạnh của hình vuông trước nó. Nếu hình vuông đầu tiên có cạnh dài 40cm thì trên tia Ox cần có một đoạn thẳng bằng bao nhiêu xentimét để có thể xếp được tất cả các hình vuông đó?
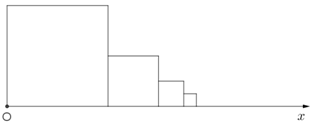
Đáp án B.
Tổng các cạnh nằm trên tia Ox của các canh hình vuông đó là:
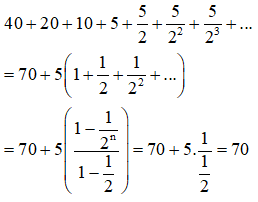
Câu 24:
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng chứa đường thẳng và vuông góc với mặt phẳng .
Đáp án C.

Câu 25:
Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức . Khi đó tam giác ABC:
Đáp án B.

Câu 26:
Hình vẽ bên giống với đồ thị của hàm số nào nhất trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây? Biết rằng hàm số có dạng
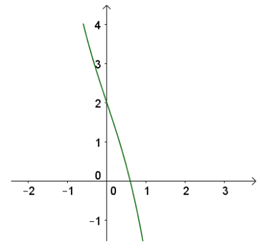
Đáp án A.
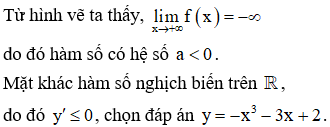
Câu 27:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và đường thẳng .
Đáp án D.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:

Câu 29:
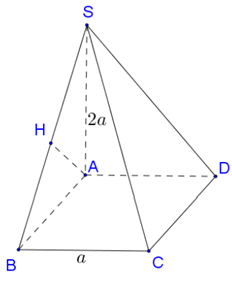
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với đáy và . Tính khoảng cách từ D đến mặt phẳng (SBC).
Đáp án B.

Câu 30:
Viết phương trình tiếp tuyến của đồ thị hàm số . Biết tiếp tuyến tạo với trục hoành một góc .
Đáp án D.
Tiếp tuyến tạo với trục hoành một góc

Câu 34:
Số nghiệm nguyên của bất phương trình là:
Đáp án A.
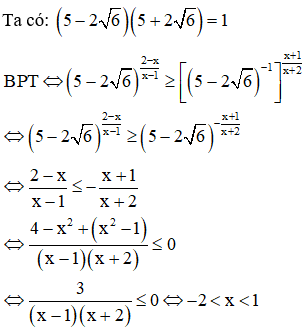
Số nghiệm nguyên của bất phương trình là {-1;0}
Câu 35:
Trong không gian cho tam giác ABC vuông tại B, . Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AB.
Đáp án B.
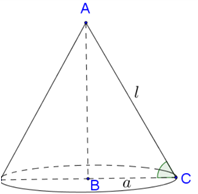
Khi quay tam giác ABC quanh cạnh AB, ta được khối nón có đỉnh A, đường sinh
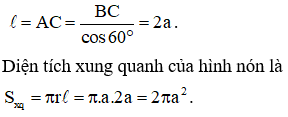
Câu 36:
Trong không gian cho tam giác ABC vuông tại B, . Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AB.
Đáp án B.

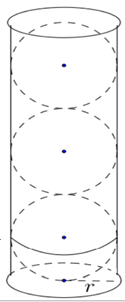
Khi quay tam giác ABC quanh cạnh AB, ta được khối nón có đỉnh A, đường sinh
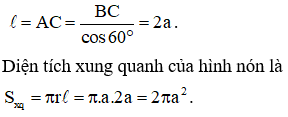
Câu 38:
Người ta bỏ vào một chiếc hộp hình trụ ba quả bóng tennis hình cầu bằng nhau, biết rằng đáy hình trụ bằng hình tròn lớn trên quả bóng, chiều cao của hình trụ gấp 3 lần đường kính quả bóng. Gọi là tổng thể tích ba quả bóng, là thể tích của hình trụ. Khi đó tỉ số là:
Đáp án D.

Câu 40:
Cho bốn số hạng liên tiếp của một cấp số cộng, có tổng của chúng bằng 16 và tổng bình phương của chúng bằng 84. Tính tổng hai bình phương số hạng đầu và số hạng cuối của bốn số hạng đó.
Đáp án C.


Tổng bình phương của số hạng đầu và cuối là
Câu 41:
Cho hình lập phương có các cạnh bằng 1. M là trung điểm CC'. Tính góc giữa hai đường thẳng AD' và BM.
Đáp án B.
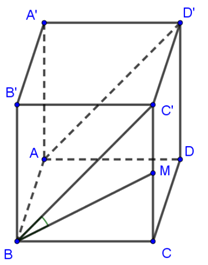
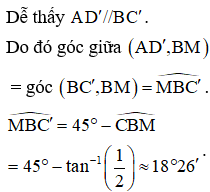
Câu 43:
Cho hình chóp tam giác S.ABC có đáy là tam giác vuông cân tại A, . Cạnh bên SA vuông góc với đáy và . Thể tích khối chóp S.ABC là:
Đáp án C.
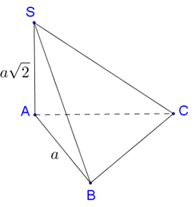
Thể tích cần tính
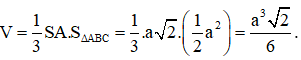
Câu 44:
Số giao điểm của đồ thị hàm số và đường thẳng là:
Đáp án A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
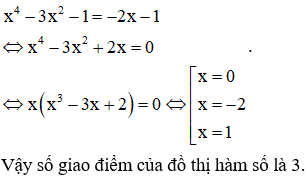
Câu 45:
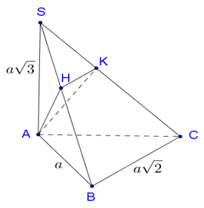
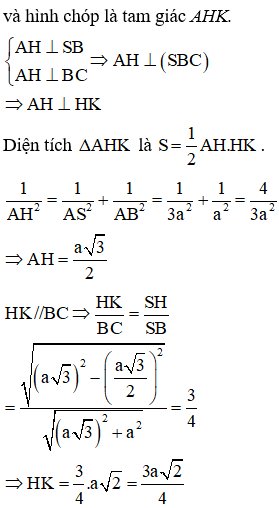
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, và SA vuông góc với mặt phẳng (ABC). Biết (P) là mặt phẳng qua A và vuông góc với SB. Diện tích thiết diện cắt bởi SB và hình chóp là:
Đáp án D.

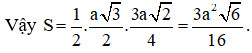
Câu 47:
Trong không gian tọa độ Oxyz, cho và . Lập phương trình mặt phẳng đi qua hai điểm A, B và tạo với một góc .
Đáp án A.

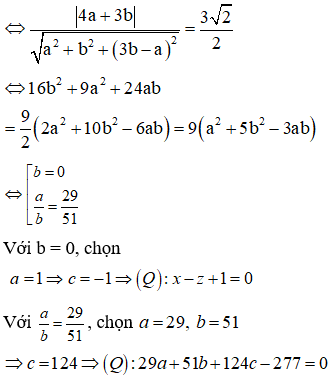
Câu 48:
Một ca nô đang chạy trên biển với tốc độ thì hết xăng. Từ thời điểm đó, ca nô chuyển động chậm dần đều với vận tốc , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc hết xăng. Hỏi từ lúc hết xăng đến khi dừng hẳn, ca nô đi được bao nhiêu mét?
Đáp án A.
Chọn mốc thời gian tại thời điểm ca nô hết xăng.
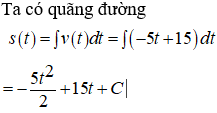
Ta xác định hằng số C dựa trên điều kiện ban đầu:
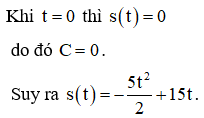
Khi ca nô dừng hẳn tương ứng với v(t) = 0 suy ra t = 3, do đó quãng đường ca nô đi được
trong thời gian 3s là s(3) = 22,5 m.
Câu 50:
Có một cái hồ rộng 50m, dài 200m. Một vận động viên chạy phối hợp với bơi (bắt buộc cả hai) cần đi từ góc này qua góc đối diện bằng cách cả chạy và bơi (như hình vẽ). Hỏi rằng sau khi chạy được bao xa (quãng đường x) thì nên nhảy xuống bơi để đến đích nhanh nhất? Biết rằng vận tốc bơi là 1,5 m/s và vận tốc chạy là 4,5 m/s.
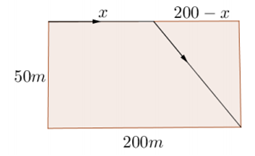
Đáp án C.
Gọi quãng đường vận động viên chạy trên bờ là x (m).
Khi đó quãng đường vận động viên bơi dưới nước sẽ là ![]()
Thời gian cho cả quãng đường đi (cả trên bờ và dưới nước) là
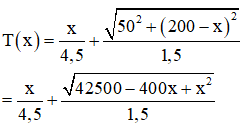
Yêu cầu bài toán tương đương với: tìm x để đạt giá trị nhỏ nhất.
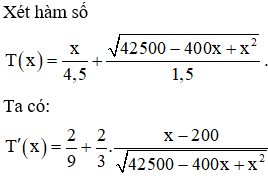
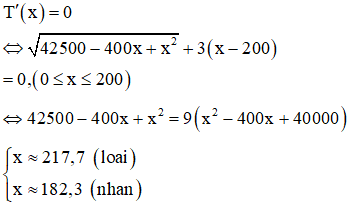
Lập bảng biến thiên ta được thì T(x) đạt giá trị nhỏ nhất.
Câu 51:
Ông Minh gửi tiết kiệm 100 triệu đồng theo hình thức lãi kép với lãi suất không đổi là 0,7% một tháng. Do nhu cầu cần chi tiêu, cứ mỗi tháng sau đó (kể từ khi gửi tiết kiệm), ông rút ra 2 triệu đồng từ số tiền của mình. Hỏi cứ như vậy thì tháng cuối cùng ông Minh rút nốt được bao nhiêu triệu đồng?
Đáp án D
Tổng quát:
Gọi A là sô tiền ban đầu ông Minh gửi (triệu đồng);
r: lãi suất/một tháng.a: số tiền mỗi tháng ông rút ra (triệu đồng);
- Sau tháng đầu tiên, số tiền cả gốc lẫn lãi ông Minh nhận được là A(1+r)
Ông rút ra a triệu đồng, số tiền còn lại là A(1+r)-a
- Sau tháng thứ hai, số tiền cả gốc lẫn lãi là ![]()
Rút ra a triệu đồng, số tiền còn lại là
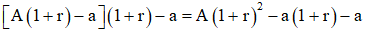
- Sau tháng thứ 3, sau khi rút ra a triệu đồng, số tiền còn lại là:
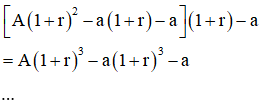
- Sau tháng thứ n, sau khi rút ra a triệu đồng, số tiền còn lại:

Giả sử sau n tháng, ông Minh rút hết số tiền, tức là:
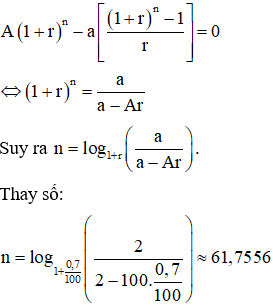
Như vậy, sau 61 tháng rút tiền thì số tiền còn lại trong tháng cuối cùng (tháng thứ 62) là: