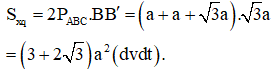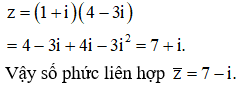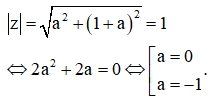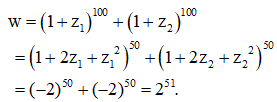51 câu hỏi trắc nghiệm thuộc Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết(Đề 17)

Câu 1:

Số phức liên hợp của số phức $z = (1 + i) (4 - 3 i)$ là

A. $\bar{z} = 7 - i$

B. $\bar{z} = 1 + i$

C. $\bar{z} = 1 - i$

D. $\bar{z} = 7 + i$

Xem đáp án

Đáp án A

Câu 2:

Số nào trong các số sau là số thuần ảo

A. $(2 - i) - (3 - i)$

B. $(1 - 2 i) - (1 + i)$

C. $2018 i^{2}$

D. $(2017 - i) + (2018 + i)$

Xem đáp án

Đáp án B

$(1 - 2 i) - (1 + i)$ = -3i là số thuần ảo.

$2018 i^{2}$ = -2018 là số thuần thực.

$(2017 - i) + (2018 + i)$ = 4035 là số thuần thực.

$(2 - i) - (3 - i)$ = -1 là số thuần thực.

Câu 3:

Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức $i^{3}, \frac{3 - i}{1 - i}, \frac{(5 + 3 i) (1 - i)}{2}$ . Khi đó tam giác ABC

A. đều

B. vuông cân tại C

C. vuông cân tại B

D. vuông cân tại A

Xem đáp án

Đáp án C

Câu 4:

Để số phức $z = a + (1 + a) i (a \in ℝ)$ có $|z| = 1$ thì

A. $a = - \frac{1}{2}$

B. |a| = 1

C. $a = - 1 h o ặ c a = 0$

D. $a = \frac{1}{2}$

Xem đáp án

Đáp án C

Câu 5:

Gọi $z_{1}, z_{2}$ là nghiệm phức của phương trình $z^{2} + 2 z + 3 = 0$ . Đặt $w = {(1 + z_{1})}^{100} + {(1 + z_{2})}^{100}$ .Khi đó w bằng

A. $2^{51}$

B. $- 2^{51}$

C. $2^{51}$ i

D. $- 2^{51}$ i

Xem đáp án

Đáp án A

Câu 6:

Tìm công thức số hạng tổng quát $(u_{n})$ biết $u_{1} = 1; u_{n} = \frac{u_{n}}{u_{n} + 2}, \forall n \in N *$ .

A. $u_{n} = \frac{1}{2^{n} + 1}$

B. $u_{n} = \frac{1}{2^{n} - 1}$

C. $u_{n} = 2^{n} - 1$

D. $u_{n} = 2^{n} + 1$

Xem đáp án

Đáp án B

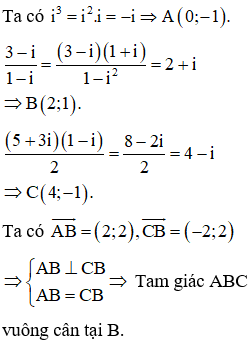
Câu 7:

Một chi đoàn có 3 đoàn viên nữ và một số đoàn viên nam. Cần lập một đội thanh niên tình nguyện (TNTN) gồm 4 người. Biết xác suất để trong 4 người được chọn có 3 nữ bằng $\frac{2}{5}$ lần xác suất 4 người được chọn toàn nam. Hỏi chi đoàn đó có bao nhiêu đoàn viên?

A. 10

B. 12

C. 11

D 9

Xem đáp án

Đáp án D

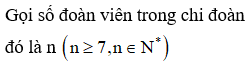
Suy ra số đoàn viên nam trong chi đoàn là n−3.

Câu 8:

Số điểm biểu diễn nghiệm của phương trình $\cos^{2} x + \sin x \cos x + \cos x - \sin x = 0$ trên đường tròn lượng giác là

A. 4

B. 2

C. 1

D. 3

Xem đáp án

Đáp án C

Nhận thấy cosx = 0 không phải là nghiệm của phương trình. Chia cả hai vế của phương trình cho cosx ta được

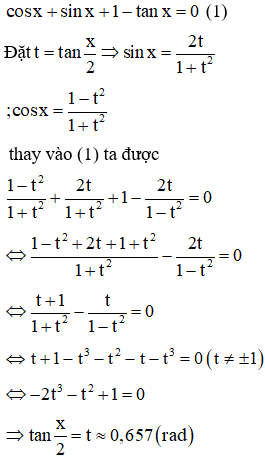
Vậy có 1 điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác.

Câu 9:

Tìm m để hàm số $y = f (x) = \{\begin{cases} \frac{\sqrt{x^{2} + 3 x} - 2}{x - 1} k h i x > 1 \\ m x + 2 k h i x \leq 1 \end{cases}$ liên tục tại $x = 1$

A. $m = - \frac{3}{2}$

B. $m = \frac{3}{4}$

C. m = -3

D. $m = - \frac{3}{4}$

Xem đáp án

Đáp án D

Câu 10:

Cho hàm số $y = (x^{2} + 2 x - 2) e^{x}$ . Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên $[0; 1]$ bằng bao nhiêu?

A. e

B. 2e

C. -2e

D. -e

Xem đáp án

Đáp án C

TXĐ: D= R.

Ta có y′=(2x+2)ex+(x2+2x−2)ex=(x2+4x)ex=0⇔[x=−4x=0.

Ta có bảng biến thiên

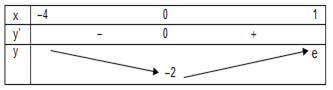
Vậy GTLN và GTNN của hàm số trên [0;1] lần lượt bằng e và −2.

Câu 11:

Một người gửi tiết kiệm 100 triệu kỳ hạn 9 tháng với lãi suất 6,5% một năm. Biết lãi được tính hàng tháng, tiền lãi mỗi tháng không cộng dồn vào từng tháng để tính lãi cho các tháng tiếp theo mà chỉ được cộng dồn khi hết kỳ hạn gửi mà người đó không lĩnh tiền thì nó mới được cộng dồn và tự động gia hạn với kỳ hạn mới mà bạn đã đăng ký trước đó. Tính số tiền mà người đó nhận được sau 9 tháng.

A. 105,324 triệu đồng

B. 103,785 triệu đồng

C. 104,875 triệu đồng

D. 90,765 triệu đồng

Xem đáp án

Đáp án C

Số tiền người đó nhận được sau 9 tháng là

100+100.0,065.9/12=104,875(trieu).

Câu 12:

Tập xác định của hàm số $y = \log_{x - 1} \sqrt{x^{2} - 1}$ là

A. x < -1 hoặc x > 1

B. x > 1

C. $\{\begin{cases} x > 1 \\ x \neq 2 \end{cases}$

D. $x \neq 2$

Xem đáp án

Đáp án C

Điều kiện:

Câu 13:

Tính $16^{- 0, 75} + {(\frac{1}{8})}^{\frac{1}{3}} - {(\frac{1}{32})}^{\frac{3}{5}}$

A. 4

B. 2

C. $\frac{1}{4}$

D. $\frac{1}{2}$

Xem đáp án

Đáp án D

Câu 14:

Cho hàm số $f (x) = \ln (2 x - x^{2})$ . Chọn khẳng định đúng trong các khẳng định sau.

A. f'(1) = 0

B. f'(2) = 0

C. f'(0) = 1

D. $f (3) = \frac{3}{4}$

Xem đáp án

Đáp án A

Câu 15:

Phương trình ${(2 - \sqrt{3})}^{x} + {(2 + \sqrt{3})}^{x} - 4 = 0$ có tổng bình phương các nghiệm là

A. 3

B. 1

C. 2

D. 0

Xem đáp án

Đáp án C

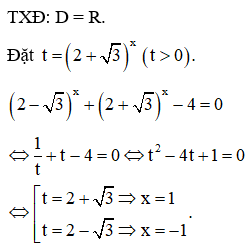
Vậy tổng bình phương các nghiệm của phương trình

Câu 16:

Tìm m để phương trình $4 {(\log_{3} \sqrt{x})}^{2} - \log_{\frac{1}{3}} x + m = 0$ có nghiệm thuộc khoảng (0;1).

A. $m \leq \frac{1}{4}$

B. $m > \frac{1}{4}$

C. $0 < m < \frac{1}{4}$

D. $0 \leq m \leq \frac{1}{4}$

Xem đáp án

Đáp án A

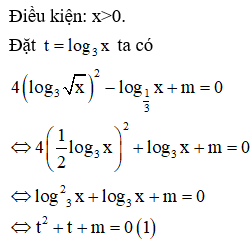
Để thỏa mãn đề bài thì (1) phải có nghiệm âm (có hai nghiệm âm, có một nghiệm âm) hay

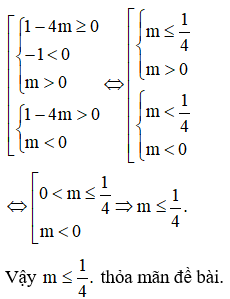
Câu 17:

Tổng các nghiệm của phương trình $2 \log_{8} 2 x + \log_{8} {(x - 1)}^{2} = \frac{4}{3}$ bằng

A. 2

B. 5

C. 4

D. 3

Xem đáp án

Đáp án A

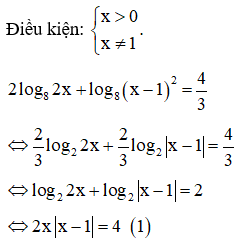
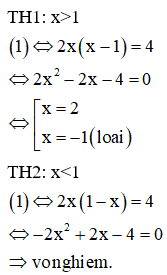
Vậy tổng các nghiệm của phương trình bằng 2.

Câu 18:

Trong mặt phẳng tọa độ Oxy cho hai đường thẳng song song a và b lần lượt có phương trình $2 x - y + 4 = 0$ và $2 x - y - 1 = 0$ . Tìm giá trị thực của tham số m để phép tịnh tiến T theo vectơ biến đường thẳng a thành đường thẳng b.

A. m = 3

B. m = 2

C. m = 4

D. m = 1

Xem đáp án

Đáp án D

Chọn A(0;4) thuộc d.

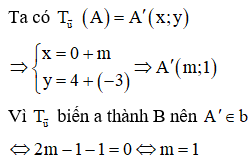
Câu 19:

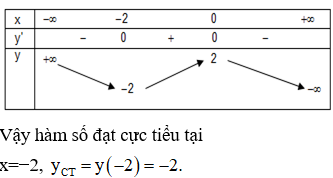
Hàm số $y = - x^{3} - 3 x^{2} + 2$ có giá trị cực tiểu y_CT là

A. $y_{C T} = - 6$

B. $y_{C T} = - 2$

C. $y_{C T} = 2$

D. $y_{C T} = - 4$

Xem đáp án

Đáp án B

TXĐ: D = R.

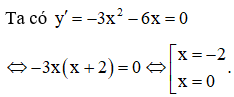
Ta có bảng biến thiên của hàm số

Câu 20:

Cho hàm số $y = x^{3} - 3 x^{2} + 1$ . Khẳng định nào sau đây là SAI?

A. Giá trị cực đại của hàm số $y_{C D} = 1$

B. Giá trị cực tiểu của hàm số $y_{C T} = - 3$

C. Hàm số đồng biến trên khoảng(1;+∞)

D. Hàm số đạt cực đại tại x = 0

Xem đáp án

Đáp án C

TXĐ: D = R.

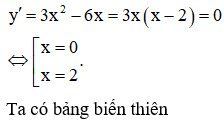
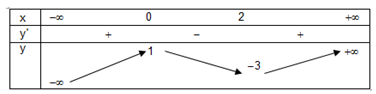
Dựa vào bảng biến thiên ta thấy

Câu 21:

Đường thẳng $y = 3 - x$ cắt đồ thị hàm số $y = x^{3} - 3 x^{2}$ tại điểm có tọa độ $(x_{0}, y_{0})$ thì

A. $y_{0} = - 2$

B. $y_{0} = 0$

C. $y_{0} = 2$

D. $y_{0} = 3$

Xem đáp án

Đáp án B

Hoành độ giao điểm của đường thẳng $y = 3 - x$ và đồ thị hàm số $y = x^{3} - 3 x^{2}$ là nghiệm của phương trình

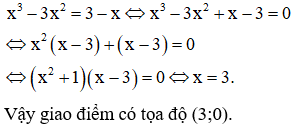
Câu 22:

Giá trị lớn nhất của hàm số $y = \frac{x^{2} + 2 x + 1}{x - 1}$ trên đoạn $[- 1; 2]$ là

A. 9

B. 0

C. Không tồn tại

D. 8

Xem đáp án

Đáp án C

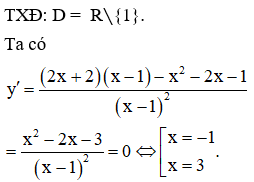
Ta có bảng biến thiên

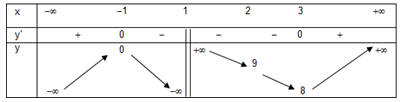
Dựa vào bảng biến thiên ta thấy, không tồn tại giá trị nhỏ nhất của hàm số trong đoạn [−1;2].

Câu 23:

Tìm tất cả các giá trị của tham số m để ba điểm cực trị của đồ thị hàm số $y = x^{4} + (2 m - x) x^{2} + 1 - m$ là ba đỉnh của một tam giác vuông

A. m = -1

B. m = 1

C. m = 0 hoặc m = 1

D. = 0

Xem đáp án

Đáp án D

TXĐ: D= R.

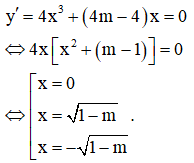
Hàm số có ba điểm cực trị khi và chỉ khi m < 1.

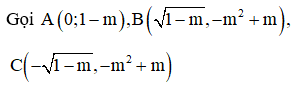
lần lượt là ba điểm cực trị của đồ thị hàm số.

Để ABC là tam giác vuông cân thì

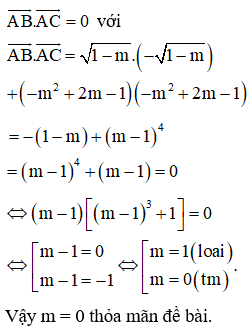
Câu 24:

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số liệt kê ở bốn phương án A,B,C,D dưới đây. Hỏi hàm số đó là hàm số nào?

A. $y = - x^{4} + 2 x^{2}$

B. $y = - x^{4} - 2 x^{2}$

C. $y = x^{4} + 2 x^{2} + 1$

D. $y = x^{4} - 2 x^{2}$

Xem đáp án

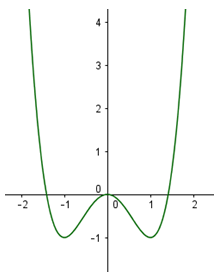
Đáp án D

Các phương án đưa ra đều là các hàm trùng phương. Nhận thấy

Nhận thấy đồ thị hàm số qua điểm (0;0) vậy hàm số cần tìm là $y = x^{4} - 2 x^{2}$

Câu 25:

Đường thẳng $y = x + m$ cắt đồ thị hàm số $y = \frac{x}{x - 1}$ tại hai điểm phân biệt khi

A. $m \in ℝ$

B. -2 < m < 2

C. -4 < m < 0

D. 0 < m < 4

Xem đáp án

Đáp án A

Điều kiện: x ≠ 1.

Hoành độ giao điểm của đường thẳng y = x + m và đồ thị hàm số $y = \frac{x}{x - 1}$ là nghiệm của phương trình

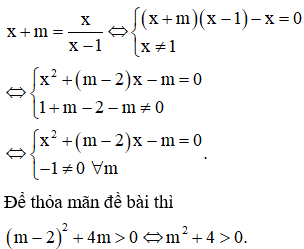
Vậy đường thẳng $y = x + m$ cắt đồ thị hàm số $y = \frac{x}{x - 1}$ tại hai điểm phân biệt với mọi m.

Câu 26:

Số đường tiệm cận của đồ thị hàm số $y = \frac{3 x - 1}{\sqrt{x^{2} + x + 2}}$ là

A. 0

B. 3

C. 1

D. 2

Xem đáp án

Đáp án D

Ta có

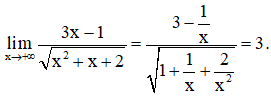
Vậy y = 3 là một tiệm cận ngang của đồ thị hàm số.

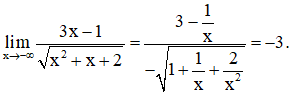
Vậy y = −3 là một tiệm cận ngang của đồ thị hàm số.

Câu 27:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = \frac{\cos x + m}{c o s x - m}$ nghịch biến trên $(\frac{π}{2}; π)$

A. $m \leq - 1$

B. -1 < m < 0

C. $- 1 \leq m \leq 0$

D. $m \geq 0$

Xem đáp án

Đáp án A

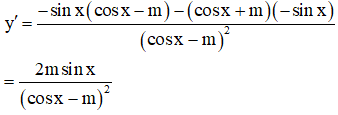
Để hàm số nghịch biến trên $(\frac{π}{2}; π)$ ta cần có

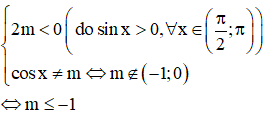
Câu 28:

Tìm độ dài các cạnh góc vuông của tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0)

A. $\frac{a}{5}; \sqrt{\frac{3}{5}} a$

B. $\frac{a}{3}; \frac{2 \sqrt{2}}{3} a$

C. $\frac{a}{2}; \frac{a}{2}$

D. $\frac{a}{3}; \frac{a \sqrt{3}}{3}$

Xem đáp án

Đáp án D

Gọi độ dài một cạnh góc vuông của tam giác vuông là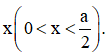

Khi đó độ dài cạnh huyền là a−x.

Độ dài cạnh góc vuông còn lại của tam giác vuông là

Ta có diện tích tam giác vuông

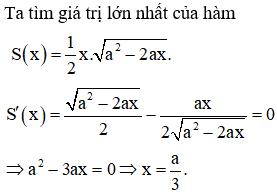
Ta có bảng biến thiên

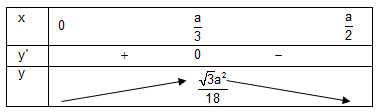
Vậy diện tích của tam giác là lớn nhất khi một cạnh góc vuông bằng

Câu 29:

Nguyên hàm của hàm số $y = e^{- 2 x + 1}$ là

A. $\int_{}^{} e^{- 2 x + 1} d x = - \frac{1}{2} e^{- 2 x + 1} + C$

B. $\int_{}^{} e^{- 2 x + 1} d x = 2 e^{- 2 x + 1} + C$

C. $\int_{}^{} e^{- 2 x + 1} d x = \frac{1}{2} e^{- 2 x + 1} + C$

D. $\int_{}^{} e^{- 2 x + 1} d x = - 2 e^{- 2 x + 1} + C$

Xem đáp án

Đáp án A

Câu 30:

Nguyên hàm của hàm số $y = e^{- 2 x + 1}$ là

A. $\int_{}^{} e^{- 2 x + 1} d x = - \frac{1}{2} e^{- 2 x + 1} + C$

B. $\int_{}^{} e^{- 2 x + 1} d x = 2 e^{- 2 x + 1} + C$

C. $\int_{}^{} e^{- 2 x + 1} d x = \frac{1}{2} e^{- 2 x + 1} + C$

D. $\int_{}^{} e^{- 2 x + 1} d x = - 2 e^{- 2 x + 1} + C$

Xem đáp án

Đáp án A

Câu 31:

Tích phân $I = \int_{1}^{2} x \ln x d x$ có giá trị bằng

A. 2ln2-2

B. $2 \ln 2 - \frac{3}{4}$

C. ln2-4

D. $2 \ln 2 - \frac{5}{2}$

Xem đáp án

Đáp án B

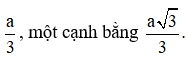
Câu 32:

Giả sử f(x) là hàm liên tục trên R và các số thực a<b<c. Mệnh đề nào sau đây sai?

A. $\int_{a}^{b} f (x) d x = \int_{b}^{a} f (x) d x + \int_{a}^{c} f (x) d x$

B. $\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x - \int_{b}^{c} f (x) d x$

C. $\int_{a}^{c} f (x) d x = \int_{b}^{a} f (x) d x + \int_{b}^{c} f (x) d x$

D. $\int_{a}^{b} c f (x) d x = - c \int_{b}^{a} f (x) d x$

Xem đáp án

Đáp án A

Ta có a<b<c suy ra

Câu 33:

Có bao nhiêu số $a \in (0; 10 π)$ sao cho $\int_{0}^{a} \sin^{3} x . \sin 2 x d x = \frac{2}{5}$ ?

A. 5

B. 4

C. 10

D. 6

Xem đáp án

Đáp án A

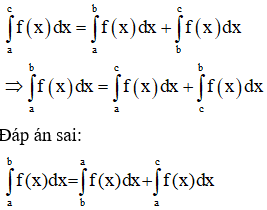
Câu 34:

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = |x|$ , trục tung, trục hoành và đường thẳng $x = 1$ là

A. 1

B. 2

C. $\frac{1}{2}$

D. $\frac{3}{2}$

Xem đáp án

Đáp án C

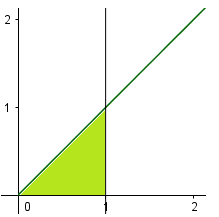
Cách 1: Diện tích hình phẳng cần tìm

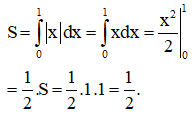
Cách 2: Diện tích hình phẳng cần tìm S=12.1.1=12.

Câu 35:

F(x) là một nguyên hàm của hàm số $y = \frac{\cos x}{1 + \sin x}$ , biết $F (0) = 1$ . Tìm F(x).

A. $\ln |1 + \sin x| + 1$

B. $- \ln |1 + \sin x| + 1$

C. $- \ln (1 + \sin x) - 1$

D. $- \ln (1 + \sin x) + 1$

Xem đáp án

Đáp án A

Câu 36:

Một ô tô đang chạy đều với vận tốc 15m/s thì phía trước xuất hiện chướng ngại vật nên người lái đạp phanh gấp. Kể từ thời điểm đó, ô tô chuyển động chậm dần đều với gia tốc $a m / s^{2}$ . Biết ôtô chuyển động được thêm 30m thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây?

A. (2;3)

B. (4;5)

C. (5;6)

D. (3;5)

Xem đáp án

Đáp án D

Phương trình vận tốc của ô tô v=15−at (m/s).

Khi ô tô dừng lại tức là vận tốc của ô tô bằng 0 hay

Quãng đường ô tô đi được từ lúc đạp phanh là

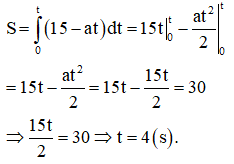
Câu 37:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(P) : x - y + z + 3 = 0$ và ba điểm $A (0; 1; 2), B (1; 1; 1), C (2; - 2; 3)$ . Tọa độ điểm M thuộc (P) sao cho $|\vec{M A} + \vec{M B} + \vec{M C}|$ nhỏ nhất là

A. M(0;0;-3)

B. M(1;1;-3)

C. M(-1;2;0)

D. M(2;1;-1)

Xem đáp án

Đáp án C

hay M là hình chiếu của G lên mặt phẳng (P).

Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).

Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)

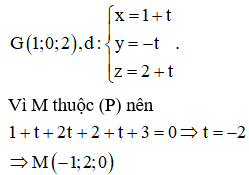
Câu 38:

Mặt phẳng $(P) : x - 2 z + 1 = 0$ có một véctơ pháp tuyến là

A. $\vec{n} = (- 2; 1; 0)$

B. $\vec{n} = (1; 0; - 2)$

C. $\vec{n} = (2; 0; - 3)$

D. $\vec{n} = (1; - 2; 0)$

Xem đáp án

Đáp án B

Mặt phẳng $(P) : x - 2 z + 1 = 0$ nhận $\vec{n} = (1; 0; - 2)$ là một véctơ pháp tuyến.

Câu 39:

Trong không gian với hệ trục tọa độ Oxyz, cho véctơ $\vec{M N} = (- 1; 0; 2)$ và $M (1; 0; 1)$ thì tọa độ điểm N là

A. N(2;0;-1)

B. N(0;0;3)

C. N(0;0;1)

D. N(-2;0;1)

Xem đáp án

Đáp án B

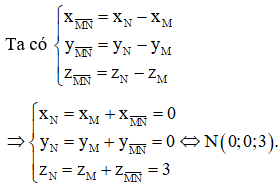
Câu 40:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{- 1} = \frac{y + 2}{3} = \frac{z + 1}{2}$ và mặt phẳng $(α) : 3 x + y - 1 = 0$ .Khẳng định nào đúng trong các khẳng định sau?

A. d thuộc mặt phẳng (α)

B. d cắt nhưng không vuông góc với (α)

C. d vuông góc với (α)

D. d song song với (α)

Xem đáp án

Đáp án A

Câu 41:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \{\begin{cases} x = 1 - t \\ y = 2 t \\ z = 2 + 2 t \end{cases}$ và mặt phẳng $(P) : x + y - z - 1 = 0$ . Giao điểm M của d và (P) có tọa độ là

A. M(1;0;2)

B. M(3;-4;-2)

C. M(0;2;4)

D. M(1;1;1)

Xem đáp án

Đáp án B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Câu 42:

Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm $A (2; 0; 0), B (0; 3; 0), C (0; 0; 1)$ . Phương trình của α là

A. $\frac{x}{2} = \frac{y}{3} = \frac{z}{1}$

B. $\frac{x}{2} + \frac{y}{3} + \frac{z}{1} = 0$

C. $3 x + 2 y - 6 z = 0$

D. $\frac{x}{2} + \frac{y}{3} + \frac{z}{1} = 1$

Xem đáp án

Đáp án D

Phương trình theo đoạn chắn của mặt phẳng (α) là $\frac{x}{2} + \frac{y}{3} + \frac{z}{1} = 1$

Câu 43:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \{\begin{cases} x = 1 - 2 t \\ y = 2 t \\ z = 1 - 5 t \end{cases}, t \in ℝ$ . Véctơ nào dưới đây là véctơ chỉ phương của d?

A. $\vec{u} = (2; 0; - 5)$

B. $\vec{u} = (2; - 2; - 5)$

C. $\vec{u} = (- 2; 2; 5)$

D. $\vec{u} = (- 2; 0; 5)$

Xem đáp án

Đáp án C

Đường thẳng d nhận $\vec{u} = (- 2; 2; 5)$ là một véctơ chỉ phương.

Câu 44:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $∆ : \{\begin{cases} x = 1 + t \\ y = 1 + m t \\ z = - 2 t \end{cases}$ và mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y - 2 z + 2 = 0$ . Với điều kiện nào của m thì đường thẳng Δ cắt (S) tại hai điểm phân biệt?

A. $- \frac{3 + \sqrt{57}}{3} < m < - \frac{3 - \sqrt{57}}{3}$

B. $m < - \frac{6 + \sqrt{114}}{3}$ hoặc $m > - \frac{6 - \sqrt{114}}{3}$

C. $- \frac{6 + \sqrt{114}}{3} m < - \frac{6 - \sqrt{114}}{3}$ hoặc $m > - \frac{6 - \sqrt{114}}{3}$

D. $m < - \frac{3 + \sqrt{57}}{3}$ hoặc $m > - \frac{3 - \sqrt{57}}{3}$

Xem đáp án

Đáp án B

Mặt cầu (S) có tâm I(1;−2;1), bán kính R=2.

Để đường thẳng cắt mặt cầu (S) tại hai điểm phân biệt thì khoảng cách từ tâm I đến đường thẳng Δ phải nhỏ hơn bán kính R.

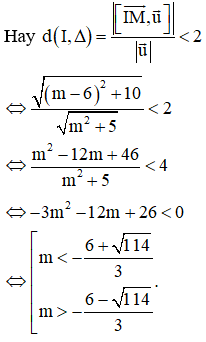
Câu 45:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có $A B = a, B C = 3 a .$ Hai mặt phẳng (SAB) và mặt phẳng (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc $30 °$ . Tính thể khối chóp S.ABCD theo a.

A. $\sqrt{30} a^{3} (d v t t)$

B. $\sqrt{10} a^{3} (d v t t)$

C. $\frac{\sqrt{10}}{3} a^{3} (d v t t)$

D. $\frac{\sqrt{30} a^{3}}{3} (d v t t)$

Xem đáp án

Đáp án D

Câu 46:

Số cạnh của một hình bát diện đều là

A. 16

B. 12

C. 4

D. 8

Xem đáp án

Đáp án B

Một hình bát diện đều có 12 cạnh.

Câu 47:

Một hình lập phương có diện tích toàn phần là $150 c m^{2}$ . Thể tích của khối lập phương là

A. 125 $c m^{3}$

B. 216 $c m^{3}$

C. 81 $c m^{3}$

D. 64 $c m^{3}$

Xem đáp án

Đáp án A

Gọi cạnh của hình lập phương là a(cm).

Diện tích toàn phần của hình lập phương

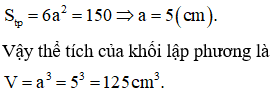
Câu 48:

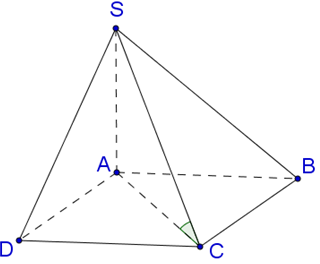
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, $S A = S B = S C = a .$ Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là

A. $\frac{a^{3}}{3}$

B. $a^{3}$

C. $\frac{a^{3}}{24}$

D. $\frac{a^{3}}{12}$

Xem đáp án

Đáp án C

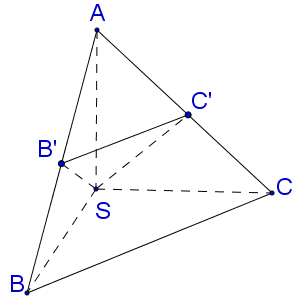
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.

Ta có:

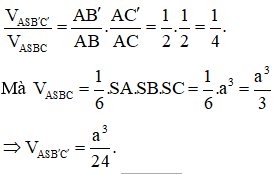
Câu 49:

Cho khối chóp S.ABC có SA=a, SB=2a, SC=3a. Thể tích lớn nhất của khối chóp là

A. $\sqrt{3} a^{3} (d v t t)$

B. $3 a^{3} (d v t t)$

C. $2 a^{3} (d v t t)$

D. $a^{3} (d v t t)$

Xem đáp án

Đáp án D

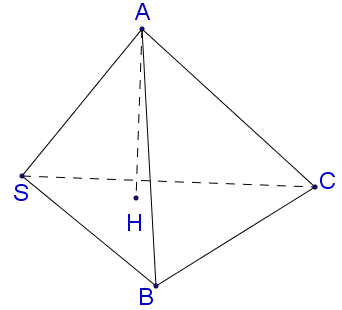
Gọi H là hình chiếu của S lên mặt phẳng (ABC).

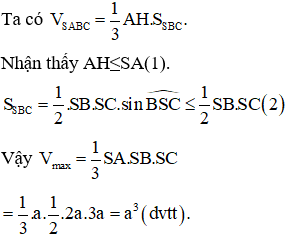
Dấu “=” xảy ra khi SA,SB,SC vuông góc với nhau từng đôi một.

Câu 50:

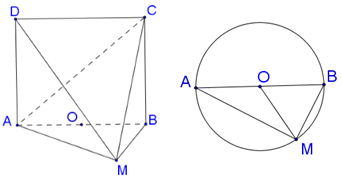
Cho hình trụ thiết diện qua trục hoành là hình vuông ABCD cạnh $4 \sqrt{3} c m$ với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung AB sao cho $\hat{A B M} = 60 °$ . Tính thể tích của khối tứ diện ACDM.

A. 3 $c m^{3}$

B. 24 $c m^{3}$

C. 6 $c m^{3}$

D. 8 $c m^{3}$

Xem đáp án

Đáp án B

Câu 51:

Cho hình lăng trụ đứng $A B C . A' B' C'$ có tam giác ABC cân tại A và $A B = a, \hat{B A C} = 120 °$ . Góc giữa đường thẳng AB′ và mặt phẳng (ABC) bằng $60 °$ . Diện tích xung quanh của khối lăng trụ $A B C . A' B' C'$ là

A. $3 a^{2}$

B. $(3 + 2 \sqrt{3}) a^{2}$

C. $2 \sqrt{3} a^{2}$

D. $\sqrt{3} a^{2}$

Xem đáp án

Đáp án B

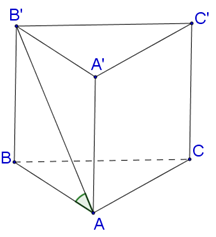
Vậy diện tích xung quanh của lăng trụ đứng ABCA′B′C′ là

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết

Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết(Đề 17)

Danh sách câu hỏi

Bài thi liên quan