Khẳng định nào sau đây là đúng ?
A. y = |tan x| đồng biến trong [;]
B. y = |tan x| là hàm số chẵn trên D = R\ { + kπ | k ∈ Z}
C. y = |tan x| có đồ thị đối xứng qua gốc tọa độ.
D. y = |tan x| luôn nghịch biến trong (;)
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án B
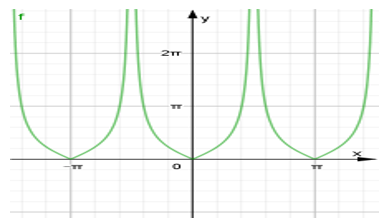
Ta được đồ thị như hình vẽ trên.
Ta thấy hàm số y = |tan x| nghịch biến trên (-π/2; 0) và đồng biến trên (0; π/2) . Nên ta loại A và D.
Với B ta có f(-x) = |tan(-x)| = | - tan x |= |tan x| = f(x) => hàm số y = |tan x| là hàm số chẵn.
Hàm số chẵn, nhận trục Oy làm trục đối xứng, không nhận tâm O làm tâm đối xứng.
Nên phương án C là sai
Nghiệm âm lớn nhất và nghiệm dương nhỏ của phương trình sin4x + cos5x = 0 theo thứ tự là:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: y = sin6x + cos6x
Tìm tổng các nghiệm của phương trình: sin(5x +) = cos(2x -) trên [0; π]
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y = tanx, x ∈ [; ]
Cho hàm số sau chọn khẳng định đúng: y = 2sin2x – sin2x + 7
Tìm giá trị lớn nhất của hàm số sau y = sinx - trong khoảng 0 < x < π
Cho hàm số sau y = tan2x – tanx + 2, x ∈ [;]. Chọn khẳng định đúng
Tìm m để các bất phương trình sau đúng với mọi x:
(3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1