 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Đáp án đúng là: D
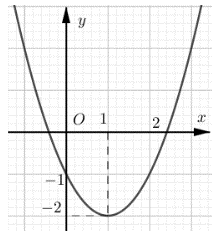
+ Quan sát đồ thị, ta thấy parabol có bề lõm quay lên trên nên a > 0.
Do đó ta loại phương án A vì a = –1 < 0.
+ Quan sát đồ thị, ta thấy parabol có trục đối xứng là đường thẳng x = 1.
⦁ Ở phương án B, đồ thị của hàm số y = x2 + 2x – 2 có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}} = - \frac{2}{{2.1}} = - 1 \ne 1\).
Do đó ta loại phương án B.
⦁ Ở phương án C, đồ thị của hàm số y = 2x2 – 4x – 2 có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}} = - \frac{{ - 4}}{{2.2}} = 1\).
• Ở phương án D, đồ thị của hàm số y = x2 – 2x – 1 có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1\).
+ Quan sát đồ thị, ta thấy parabol đi qua điểm A(0; –1).
• Thay x = 0, y = –1 vào hàm số ở phương án C, ta có: –1 = 2.02 – 4.0 – 2 (vô lí).
Do đó đồ thị của hàm số ở phương án C không đi qua điểm A(0; –1).
Vì vậy ta loại phương án C.
• Thay x = 0, y = –1 vào hàm số ở phương án D, ta có –1 = 02 – 2.0 – 1 (đúng).
Do đó đồ thị của hàm số ở phương án D đi qua điểm A(0; –1).
Vậy ta chọn phương án D.
Cho hàm số y = ax2 + bx + c có đồ thị như hình vẽ:
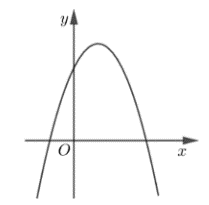
Mệnh đề nào dưới đây đúng?
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - 2x + 1,\,\,\,\,khi\,\,x \le - 3\\\frac{{x + 7}}{2},\,\,\,\,\,\,\,\,khi\,\,x > - 3\end{array} \right.\). Nếu f(x0) = 5 thì x0 bằng:
Xét tính đồng biến, nghịch biến của hàm số \(y = \sqrt[3]{x} + 3\).
Cho hàm số \[y = h\left( x \right) = \left\{ \begin{array}{l} - 2\left( {{x^2} + 1} \right),\,\,\,khi\,\,x \le 1\\4\sqrt {x - 1} ,\,\,\,\,\,\,\,\,\,\,khi\,\,x > 1\end{array} \right.\]. Khi đó \(h\left( {\frac{{\sqrt 2 }}{2}} \right)\) bằng:
Cho hàm số \(f\left( x \right) = \sqrt {2x - 7} \). Khẳng định nào sau đây đúng?
Cho hàm số y = f(x) xác định trên đọa [–3; 3] và có đồ thị được biểu diễn như hình bên:
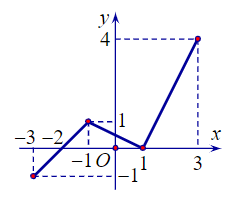
Khẳng định nào sau đây đúng?