Cho hàm số $y=f\left(x\right)=\frac{2x^2+\left|x+1\right|}{x-1}$ . Khẳng định nào sau đây đúng?

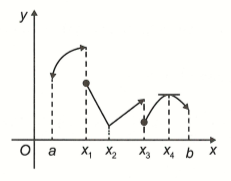
Cho đồ thị hàm số $y=f\left(x\right)$   xác định trên khoảng $\left(a;b\right)$  như hình vẽ.

Dựa vào hình vẽ hãy cho biết tại mỗi điểm   $x_1,x_2,x_3,x_4.$

a, Hàm số có liên tục không?

b, Hàm số có đạo hàm không?

Chứng minh rằng hàm số $f\left(x\right)=\frac{2x^2+\left|x+1\right|}{x-1}$  liên tục tại $x=-1$  nhưng không có đạo hàm tại điểm đó.

Chứng minh rằng hàm số $f\left(x\right)=\left\{\begin{array}{l}{\left(x-1\right)}^2,x\ge 0\\ -x^2,x<0\end{array}\right.$   không có đạo hàm tại  nhưng có đạo

hàm tại $x=2$  .

Biểu thức $\Delta y$   và $\frac{\Delta y}{\Delta x}$  của hàm số $y=x^2-1$  tính theo $x$   và $\Delta x$  là

Cho hàm số  $y=\left\{\begin{array}{l}{x}^2+ax+b\text{ khi }x\ge 2\\ x^3-x^2-8x+10\text{ khi }x<2\end{array}\right.,$ biết hàm số có đạo hàm tại điểm $x=2$ .

Giá trị của ab   bằng

Cho hàm số $y=f\left(x\right)=x+\left|x\right|$  . Giá trị $f^{\text{'}}\left(0\right)$  bằng

Dùng định nghĩa tính đạo hàm của hàm số $y=2x^2+3$  tại $x_0=2$ .

Dùng định nghĩa tính đạo hàm của hàm số $y=\sin x$  tại $x_0=\frac{\pi }{3}.$

Dùng định nghĩa tính đạo hàm của hàm số $y=\sqrt{2x-1}$tại $x_0=1.$

Dùng định nghĩa tính đạo hàm của hàm số $y=\frac{2x-1}{x+1}$  tại $x_0=3$ .

Giá trị đạo hàm của hàm số $y=\sqrt{2x-1}$  tại điểm $x_0=5$  là

Giá trị của m để hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^4-4}{x-2},\text{ khi }x\ne 2\\ m\text{ khi }x=2\end{array}\right.$  có đạo hàm tại $x=2$  bằng

Đạo hàm của hàm số $f\left(x\right)=\left\{\begin{array}{l}2x+3\text{ khi x}\ge \text{1}\\ \frac{x^3+2x^2-7x+4}{x-1}\text{ khi }x<1\end{array}\right.$  tại $x_0=1$  bằng

Đạo hàm của hàm số $y=2x+1$   tại điểm $x_0=-1$  là

Nếu hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^4-2x^2+1}{x+1}\text{ khi }x\ge -1\\ a{x}^2+ax+b\text{ khi }x<-1\end{array}\right.$  có đạo hàm trên R thì giá trị $a+b$  là