Thể tích của khối chóp
-
324 lượt thi
-
33 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:
Đáp án cần chọn là: C
Câu 2:
Phép vị tự tỉ \[k > 0\;\]biến khối chóp có thể tích V thành khối chóp có thể tích V′. Khi đó:
Đáp án cần chọn là: D
Câu 3:
Cho khối chóp tam giác S.ABC, trên các cạnh SA,SB,SC lần lượt lấy các điểm A′,B′,C′. Khi đó:
Đáp án cần chọn là: D
Câu 4:
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:
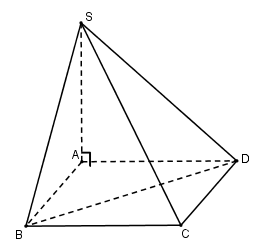
Ta có: \[{S_{{\rm{\Delta }}BCD}} = \frac{1}{2}{S_{ABCD}} = \frac{1}{2}{a^2}\]
\[{V_{S.BCD}} = \frac{1}{3}SA.{S_{BCD}} = \frac{1}{3}a.\frac{1}{2}{a^2} = \frac{{{a^3}}}{6}\]
Đáp án cần chọn là: A
Câu 5:
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn \[SA \bot \left( {ABCD} \right)\;\] và \[AB = 2AD = 2CD = 2a = \sqrt 2 SA\]. Thể tích khối chóp S.BCD là:
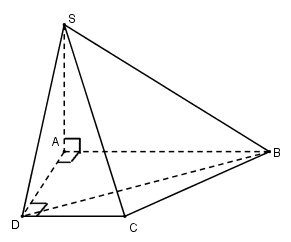
Ta có: \[{S_{ABCD}} = \frac{1}{2}\left( {AB + CD} \right).AD = \frac{1}{2}\left( {2a + a} \right)a = \frac{{3{a^2}}}{2}\]
\[{S_{{\rm{\Delta }}ABD}} = \frac{1}{2}AD.AB = \frac{1}{2}a.2a = {a^2}\]
\[ \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \frac{{3{a^2}}}{2} - {a^2} = \frac{{{a^2}}}{2}\]
\[SA = \frac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \]
\[ \Rightarrow {V_{S.BCD}} = \frac{1}{3}SA.{S_{BCD}} = \frac{1}{3}a\sqrt 2 .\frac{{{a^2}}}{2} = \frac{{{a^3}\sqrt 2 }}{6}\]
Đáp án cần chọn là: B
Câu 6:
Cho hình chóp S.ABCD có \[SA \bot (ABCD)\]. Biết \[AC = a\sqrt 2 \], cạnh SC tạo với đáy một góc 600 và diện tích tứ giác ABCD là \[\frac{{3{a^2}}}{2}\]. Gọi H là hình chiếu của A trên cạnh SC. Tính thể tích khối chóp H.ABCD.
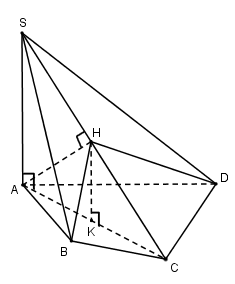
Ta có:\[SA \bot \left( {ABCD} \right) \Rightarrow AC\] là hình chiếu của SC trên
\[\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = {60^0}\]
\[SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow {\rm{\Delta }}SAC\]vuông tại A và\[\widehat {SCA} = {60^0}\]
Xét tam giác vuông SAC có:
\[SA = AC.\tan 60 = a\sqrt 2 .\sqrt 3 = a\sqrt 6 ;\,SC = \frac{{AC}}{{{\rm{cos}}60}} = \frac{{a\sqrt 2 }}{{\frac{1}{2}}} = 2a\sqrt 2 \]
Áp dụng hệ thức lượng trong tam giác vuông SAC có:
\[A{C^2} = HC.SC \Rightarrow \frac{{HC}}{{SC}} = \frac{{A{C^2}}}{{S{C^2}}} = \frac{{2{a^2}}}{{8{a^2}}} = \frac{1}{4}\]
Trong (SAC) kẻ\[HK//SA \Rightarrow HK \bot \left( {ABCD} \right)\]
Ta có:\[\frac{{HK}}{{SA}} = \frac{{HC}}{{SC}} = \frac{1}{4} \Rightarrow HK = \frac{1}{4}SA = \frac{{a\sqrt 6 }}{4}\]
Vậy\[{V_{H.ABCD}} = \frac{1}{3}HK.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 6 }}{4}.\frac{{3{a^2}}}{2} = \frac{{{a^3}\sqrt 6 }}{8}\]
Đáp án cần chọn là: C
Câu 7:
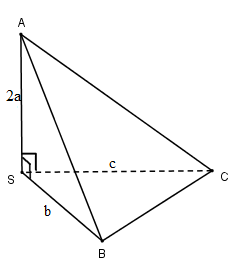
Cho hình chóp S.ABC có \[SA \bot SB,SB \bot SC,SA \bot SC;SA = 2a,SB = b,SC = c\]. Thể tích khối chóp là:
Ta có: \(\left. {\begin{array}{*{20}{c}}{SA \bot SB}\\{SA \bot SC}\\{SB \bot SC}\end{array}} \right\} \Rightarrow S.ABC.\) là tứ diện vuông.
\[ \Rightarrow {V_{S.ABC}} = \frac{1}{6}SA.SB.SC = \frac{1}{6}.2a.b.c = \frac{1}{3}abc\]
Đáp án cần chọn là: A
Câu 8:
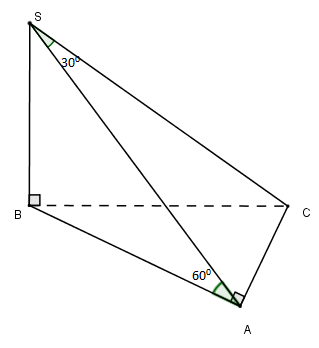
Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết SB=a,SC hợp với (SAB) một góc 300 và (SAC) hợp với đáy (ABC) một góc 600. Thể tích khối chóp là:
Ta có:
\(\left. {\begin{array}{*{20}{c}}{AC \bot AB}\\{AC \bot SB(SB \bot (ABC))}\end{array}} \right\} \Rightarrow AC \bot (SAB) \Rightarrow AC \bot SA\)
⇒SA là hình chiếu vuông góc của SC trên
\[\left( {SAB} \right) \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {\left( {SC;SA} \right)} = \widehat {CSA} = {30^0}\]
\(\left. {\begin{array}{*{20}{c}}{(SAC) \cap (ABC) = AC}\\{(SAC) \supset SA \bot AC}\\{(ABC) \supset AB \bot AC}\end{array}} \right\} \Rightarrow ((SA\widehat {C);(A}BC))\)
\[SB \bot \left( {ABC} \right) \Rightarrow SB \bot AB \Rightarrow {\rm{\Delta }}SAB\] vuông tại B
\[ \Rightarrow AB = SB.\cot {60^0} = a.\frac{1}{{\sqrt 3 }} = \frac{{a\sqrt 3 }}{3}\]
\[ \Rightarrow SA = \sqrt {S{B^2} + A{B^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{3}} = \frac{{2a}}{{\sqrt 3 }}\]
Xét tam giác vuông SAC ta có: \[AC = SA.\tan {30^0} = \frac{{2a}}{{\sqrt 3 }}.\frac{1}{{\sqrt 3 }} = \frac{{2a}}{3}\]
\[{S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}\frac{{a\sqrt 3 }}{3}.\frac{{2a}}{3} = \frac{{{a^2}\sqrt 3 }}{9}\]
\[{V_{S.ABC}} = \frac{1}{3}SB.{S_{ABC}} = \frac{1}{3}.a.\frac{{{a^2}\sqrt 3 }}{9} = \frac{{{a^3}\sqrt 3 }}{{27}}\]
Đáp án cần chọn là: A
Câu 9:
Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau, AB=6a,AC=7a,AD=4a. Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CD,DB. Thể tích V của tứ diện AMNP là:
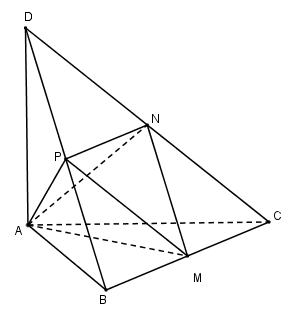
Ta có:
ABCD là tứ diện vuông tại A nên
\[{V_{ABCD}} = \frac{1}{6}AB.AC.AD = \frac{1}{6}.6a.7a.4a = 28{a^3}\]
Áp dụng công thức tính tỉ lệ thể tích các khối tứ diện ta có:
\[\frac{{{V_{DAPN}}}}{{{V_{DABC}}}} = \frac{{DA}}{{DA}}.\frac{{DP}}{{DB}}.\frac{{DN}}{{DC}} = \frac{1}{1}.\frac{1}{2}.\frac{1}{2} = \frac{1}{4} \Rightarrow {V_{DAPN}} = \frac{1}{4}{V_{DABC}} = \frac{1}{4}.28{a^3} = 7{a^3}\]
\[\frac{{{V_{BAPM}}}}{{{V_{BADC}}}} = \frac{{BA}}{{BA}}.\frac{{BP}}{{BD}}.\frac{{BM}}{{BC}} = \frac{1}{1}.\frac{1}{2}.\frac{1}{2} = \frac{1}{4} \Rightarrow {V_{BAPM}} = \frac{1}{4}{V_{BADC}} = \frac{1}{4}.28{a^3} = 7{a^3}\]
\[\frac{{{V_{CAMN}}}}{{{V_{CABD}}}} = \frac{{CA}}{{CA}}.\frac{{CM}}{{CB}}.\frac{{CN}}{{CD}} = \frac{1}{1}.\frac{1}{2}.\frac{1}{2} = \frac{1}{4} \Rightarrow {V_{CAMN}} = \frac{1}{4}{V_{CABD}} = \frac{1}{4}.28{a^3} = 7{a^3}\]
Do đó
\[{V_{AMNP}} = {V_{ABCD}} - {V_{DAPN}} - {V_{BAPM}} - {V_{CAMN}} = 28{a^3} - 7{a^3} - 7{a^3} - 7{a^3} = 7{a^3}\]
Đáp án cần chọn là: D
Câu 10:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Đường thẳng SC tạo với đáy góc 450. Gọi M,N lần lượt là trung điểm của AB và AD. Thể tích của khối chóp S.MCDN là:
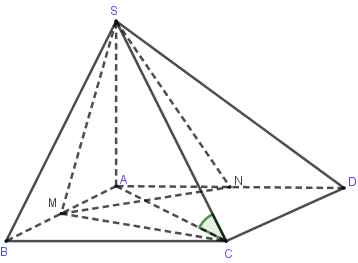
\(\left. {\begin{array}{*{20}{c}}{(SAB) \bot (ABCD)}\\{(SAD) \bot (ABCD)}\\{(SAB) \cap (SAD) = SA}\end{array}} \right\} \Rightarrow SA \bot (ABCD)\)
⇒AC là hình chiếu vuông góc của SC trên
\[\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA} = {45^0}\]
(vì\[SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow {\rm{\Delta }}SAC\] vuông tại\[A \Rightarrow \widehat {SCA} < {90^o}\])
\[ \Rightarrow SA = AC = a\sqrt 2 \]
\[{S_{ABCD}} = {a^2}\]
\[{S_{AMN}} = \frac{1}{2}AM.AN = \frac{1}{2}\frac{a}{2}\frac{a}{2} = \frac{{{a^2}}}{8}\]
\[{S_{BCM}} = \frac{1}{2}BM.BC = \frac{1}{2}\frac{a}{2}.a = \frac{{{a^2}}}{4}\]
\[ \Rightarrow {S_{MCDN}} = {S_{ABCD}} - {S_{AMN}} - {S_{BCM}} = {a^2} - \frac{{{a^2}}}{8} - \frac{{{a^2}}}{4} = \frac{{5{a^2}}}{8}\]
\[ \Rightarrow {V_{S.MCDN}} = \frac{1}{3}SA.{S_{MCDN}} = \frac{1}{3}a\sqrt 2 .\frac{{5{a^2}}}{8} = \frac{{5{a^3}\sqrt 2 }}{{24}}\]
Đáp án cần chọn là: D
Câu 11:
Cho khối lăng trụ tam giác đều ABC.A1B1C1 có tất cả các cạnh bằng a. Gọi M là trung điểm của AA1. Thể tích khối chóp M.BCA1 là:

\[\Delta ABC\] là tam giác đều cạnh aa nên có diện tích\[{S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\]
Ta có\[AM = \frac{{A{A_1}}}{2} = \frac{a}{2}\]
Hai tứ diện MABC và MA1BC có chung đỉnh C, diện tích hai đáy MAB và MA1B bằng nhau nên có thể tích bằng nhau, suy ra
\[{V_{M.BC{A_1}}} = {V_{M.ABC}} = \frac{1}{3}AM.{S_{ABC}} = \frac{{{a^3}\sqrt 3 }}{{24}}\]
Đáp án cần chọn là: B
Câu 12:
Cho hình chóp đều S.ABCD có cạnh bên và cạnh đáy bằng a. Thể tích của khối chóp S.ABCD là:
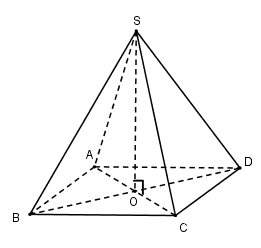
Gọi \[O = AC \cap BD\]
Vì chóp S.ABCD đều nên\[SO \bot \left( {ABCD} \right)\]
Ta có:\[AC = BD = a\sqrt 2 \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\]
\[SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow {\rm{\Delta }}SOA\] vuông tại O
\[ \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{2}} = \frac{{a\sqrt 2 }}{2}\]
Vậy\[{V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}\frac{{a\sqrt 2 }}{2}{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\]
Đáp án cần chọn là: A
Câu 13:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp S.ABC?

Gọi O là trọng tâm tam giác đều ABC
Vì chóp S.ABC đều nên\[SO \bot \left( {ABC} \right)\]
⇒OA là hình chiếu vuông góc của SA lên (ABC)
\[ \Rightarrow \widehat {\left( {SA;\left( {ABC} \right)} \right)} = \widehat {\left( {SA;OA} \right)} = \widehat {SAO} = {60^0}\]
\[SO \bot \left( {ABC} \right) \Rightarrow SO \bot OA \Rightarrow {\rm{\Delta }}SAO\] vuông tại O
Gọi D là trung điểm của BC ta có: \[AD = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AD = \frac{2}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\]
\[ \Rightarrow SO = AO.\tan 60 = \frac{{a\sqrt 3 }}{3}.\sqrt 3 = a\]
Vì tam giác ABC đều nên\[{S_{{\rm{\Delta }}ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\]
Vậy\[{V_{S.ABC}} = \frac{1}{3}SO.{S_{{\rm{\Delta }}ABC}} = \frac{1}{3}a\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{12}}\]
Đáp án cần chọn là: BCâu 14. Cho hình chóp đều S.ABCD có diện tích đáy là 16cm2, diện tích một mặt bên là \[8\sqrt 3 c{m^2}\]. Thể tích khối chóp S.ABCD là:
A.\[\frac{{32\sqrt 2 }}{3}c{m^3}\]
B. \[\frac{{32\sqrt {13} }}{3}c{m^3}\]
C. \[\frac{{32\sqrt {11} }}{3}c{m^3}\]
D. \[4c{m^3}\]Trả lời:
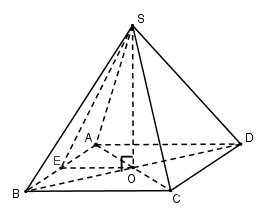
Gọi\[O = AC \cap BD\].Vì chóp S.ABCD đều nên\[SO \bot \left( {ABCD} \right)\]
Vì chóp S.ABCD đều nên ABCD là hình vuông
\[ \Rightarrow {S_{ABCD}} = A{B^2} = 16 \Rightarrow AB = 4\left( {cm} \right) = AD\]
Gọi E là trung điểm của AB⇒OE là đường trung bình của tam giác ABD
\[ \Rightarrow OE//AD \Rightarrow OE \bot AB\]và \[OE = \frac{1}{2}AD = \frac{1}{2}.4 = 2\left( {cm} \right)\]
\(\left. {\begin{array}{*{20}{c}}{OE \bot AB}\\{SO \bot AB(SO \bot (ABCD))}\end{array}} \right\} \Rightarrow AB \bot (SOE) \Rightarrow AB \bot SE\)
\[ \Rightarrow {S_{{\rm{\Delta }}SAB}} = \frac{1}{2}SE.AB = 8\sqrt 3 \Rightarrow SE = \frac{{16\sqrt 3 }}{{AB}} = \frac{{16\sqrt 3 }}{4} = 4\sqrt 3 \left( {cm} \right)\]
\[SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OE \Rightarrow {\rm{\Delta }}SOE\] vuông tại O
\[ \Rightarrow SO = \sqrt {S{E^2} - O{E^2}} = \sqrt {48 - 4} = \sqrt {44} = 2\sqrt {11} \left( {cm} \right)\]
Vậy\[{V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.2\sqrt {11} .16 = \frac{{32\sqrt {11} }}{3}\left( {c{m^3}} \right)\]
Đáp án cần chọn là: C
Câu 14:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc 600. Thể tích khối chóp S.ABC là:
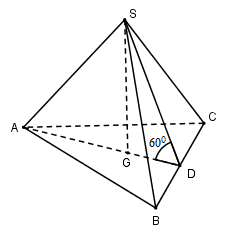
Bước 1:
Gọi G là trọng tâm tam giác ABC. Vì chóp S.ABC đều nên \[SG \bot \left( {ABC} \right)\]
Gọi D là trung điểm của BC ta có: \[AD \bot BC\]
Ta có:
\(\left. {\begin{array}{*{20}{c}}{BC \bot AD}\\{BC \bot SG(SG \bot (ABC))}\end{array}} \right\} \Rightarrow BC \bot (SAD) \Rightarrow BC \bot SD\)
\(\left. {\begin{array}{*{20}{c}}{(SBC) \cap (ABC) = BC}\\{(SBC) \supset SD \bot BC}\\{(ABC) \supset AD \bot BC}\end{array}} \right\} \Rightarrow ((SB\widehat {C);(A}BC)) = (S\widehat {D;A}D) = \widehat {SDA} = {60^0}\)
Bước 2:
Vì tam giác ABC đều cạnh a nên \[AD = \frac{{a\sqrt 3 }}{2} \Rightarrow DG = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\]
\[SG \bot \left( {ABC} \right) \Rightarrow SG \bot AD \Rightarrow {\rm{\Delta }}SGD\]vuông tại G
\[ \Rightarrow SG = GD.\tan 60 = \frac{{a\sqrt 3 }}{6}.\sqrt 3 = \frac{a}{2}\]
Bước 3:
Tam giác ABC đều \[ \Rightarrow {S_{{\rm{\Delta }}ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\]
Bước 4:
\[ \Rightarrow {V_{S.ABC}} = \frac{1}{3}SG.{S_{{\rm{\Delta }}ABC}} = \frac{1}{3}.\frac{a}{2}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{24}}\]
Đáp án cần chọn là: C
Câu 15:
Cho tứ diện đều ABCD có cạnh bằng 8. Ở bốn đỉnh tứ diện, nguời ta cắt đi các tứ diện đều bằng nhau có cạnh bằng x, biết khối đa diện tạo thành sau khi cắt có thể tích bằng \(\frac{3}{4}\) thể tích tứ diện ABCD. Giá trị của x là:
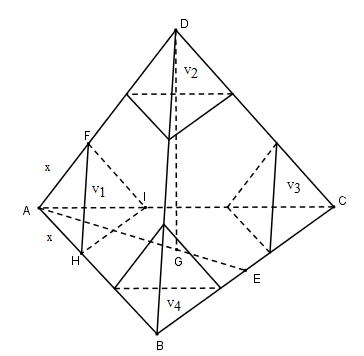
Tứ diện ABCD đều cạnh a có thể tích là \[{V_{ABCD}} = \frac{{{a^3}\sqrt 2 }}{{12}}\]
Vì tứ diện đều ABCD cạnh 8 nên\[{V_{ABCD}} = \frac{{{8^3}\sqrt 2 }}{{12}} = \frac{{128\sqrt 2 }}{3}\]
Tứ diện đều FAHI cạnh x nên\[{V_1} = \frac{{{x^3}\sqrt 2 }}{{12}}\]
Tương tự ta có:\[{V_2} = {V_3} = {V_4} = \frac{{{x^3}\sqrt 2 }}{{12}}\]
⇒Khối đa diện tạo thành sau khi cắt có thể tích là
\[V = {V_{ABCD}} - 4{V_1} = \frac{{128\sqrt 2 }}{3} - 4\frac{{{x^3}\sqrt 2 }}{{12}} = \frac{{\left( {128 - {x^3}} \right)\sqrt 2 }}{3}\]
Vì khối đa diện tạo thành sau khi cắt có thể tích bằng\[\frac{3}{4}\]thể tích tứ diện ABCDABCD nên ta có:
\[\frac{{\left( {128 - {x^3}} \right)\sqrt 2 }}{3} = \frac{3}{4}\frac{{128\sqrt 2 }}{3} \Rightarrow 128 - {x^3} = 96 \Leftrightarrow {x^3} = 32 \Rightarrow x = \sqrt[3]{{32}} = 2\sqrt[3]{4}\]
Đáp án cần chọn là: D
Câu 17:
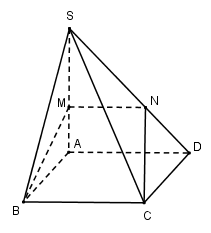
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và SA=a. Điểm M thuộc cạnh SA sao cho \(\frac{{SM}}{{SA}} = k\). Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
Vì\[BC//AD\]nên mặt phẳng (BMC) cắt (SAD) theo đoạn thẳng\[MN//AD\left( {N \in SD} \right)\]
Vì\[MN//AD \Rightarrow \frac{{SM}}{{SA}} = \frac{{SN}}{{SD}} = k\]
\[\begin{array}{*{20}{l}}{\frac{{{V_{S.MBC}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}} = k \Rightarrow {V_{S.MBC}} = k.{V_{S.ABC}} = \frac{k}{2}.{V_{S.ABCD}}}\\{\frac{{{V_{S.MNC}}}}{{{V_{S.ADC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SD}} = {k^2} \Rightarrow {V_{S.MNC}} = {k^2}.{V_{S.ADC}} = \frac{{{k^2}}}{2}.{V_{S.ABCD}}}\\{ \Rightarrow {V_{S.MBCN}} = {V_{S.MBC}} + {V_{S.MNC}} = \left( {\frac{k}{2} + \frac{{{k^2}}}{2}} \right){V_{S.ABCD}}}\end{array}\]
Để mặt phẳng (BMNC) chia hình chóp thành 2 phần có thể tích bằng nhau thì
\[\frac{k}{2} + \frac{{{k^2}}}{2} = \frac{1}{2} \Leftrightarrow {k^2} + k - 1 = 0 \Leftrightarrow k = \frac{{ - 1 + \sqrt 5 }}{2}\]do k > 0.
Đáp án cần chọn là: B
Câu 18:
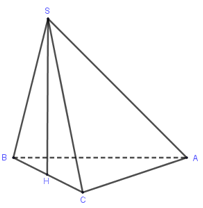
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại A,AB=a,AC=\(a\sqrt 3 \). Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC
Trong mp(SBC) kẻ \[SH \bot BC\left( {H \in BC} \right) \Rightarrow SH \bot \left( {ABC} \right),H\]là trung điểm BCBC
Xét tam giác vuông ABC có \[BC = \sqrt {{a^2} + 3{a^2}} = 2a \Rightarrow {\rm{\Delta }}SBC\]đều cạnh 2a
\[ \Rightarrow SH = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow {V_{S.ABC}} = \frac{1}{3}SH.{S_{{\rm{\Delta }}ABC}} = \frac{1}{6}SH.AB.AC = \frac{1}{2}{a^3}\]
Đáp án cần chọn là: A
Câu 19:
Cho hình chóp S.ABC có AB=AC=4,BC=2,SA=\(4\sqrt 3 \), \(\widehat {SAB} = \widehat {SAC} = {30^0}\). Tính thể tích khối chóp S.ABC.
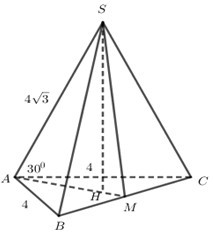
Dễ thấy\[{\rm{\Delta }}SAB = {\rm{\Delta }}SAC\left( {c.g.c} \right)\]nên SB=SC hay tam giác\[{\rm{\Delta }}SBC\] cân.
Gọi M là trung điểm BC ta có: \[AM \bot BC,SM \bot BC \Rightarrow BC \bot \left( {SAM} \right)\]
Gọi H là hình chiếu của S trên AM thì\[SH \bot AM,SH \bot BC\] nên SH là đường cao của hình chóp.
Xét tam giác SAB có:
\[S{B^2} = S{A^2} + A{B^2} - 2SA.AB\cos {30^0} = 16 \Rightarrow SB = 4 \Rightarrow SC = 4\]
Do đó
\[S{M^2} = \frac{{S{B^2} + S{C^2}}}{2} - \frac{{B{C^2}}}{4} = 15 \Rightarrow SM = \sqrt {15} \]
Tam giác ABC có\[A{M^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4} = 15 \Rightarrow AM = \sqrt {15} \]
Khi đó\[{S_{SAM}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = 6\]
Do đó:\[SH = \frac{{2{S_{SAM}}}}{{AM}} = \frac{{2.6}}{{\sqrt {15} }} = \frac{{4\sqrt {15} }}{5}\]
\[{V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SH = \frac{1}{3}.\frac{1}{2}AM.BC.SH = \frac{1}{6}.\sqrt {15} .2.\frac{{4\sqrt {15} }}{5} = 4\]
Đáp án cần chọn là: C
Câu 20:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt đáy nằm trong hình vuông ABCD. Biết rằng SA và SC tạo với đáy các góc bằng nhau, góc giữa SB và đáy bằng 450, góc giữa SD và đáy bằng α với \[tan\alpha = \frac{1}{3}\]. Tính thể tích khối chóp đã cho.
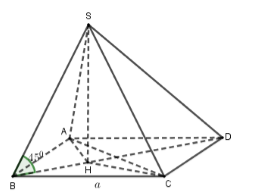
Gọi H là hình chiếu của S lên (ABCD).
Khi đó, \[\widehat {SAH} = \widehat {SCH}\] vì hai góc này lần lượt là góc tạo bởi SA,SC với mặt phẳng đáy.
\[\widehat {SBH} = {45^0},\tan \widehat {SDH} = \frac{1}{3}\]
Tam giác\[{\rm{\Delta }}SAH = {\rm{\Delta }}SCH \Rightarrow HA = HC \Rightarrow H\] nằm trên trung trực của AC.
Mà BD là đường trung trực của AC nên\[H \in BD\]
Lại có\[\widehat {SBH} = {45^0} \Rightarrow HB = HS,\tan \widehat {SDH} = \frac{1}{3} = \frac{{SH}}{{HD}}\]
\[ \Rightarrow \frac{{HB}}{{HD}} = \frac{1}{3} \Rightarrow \frac{{HB}}{{BD}} = \frac{1}{4}\]
Mà\[BD = a\sqrt 2 \Rightarrow HB = \frac{{a\sqrt 2 }}{4} \Rightarrow SH = \frac{{a\sqrt 2 }}{4}\]
Vậy\[{V_{S.ABCD}} = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{4}.{a^2} = \frac{{{a^3}\sqrt 2 }}{{12}}\]
Đáp án cần chọn là: D
Câu 21:
Cho tứ diện ABCD có G là điểm thỏa mãn \[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \]. Mặt phẳng thay đổi chứa BG và cắt AC,AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số \[\frac{{{V_{ABMN}}}}{{{V_{ABCD}}}}\] là
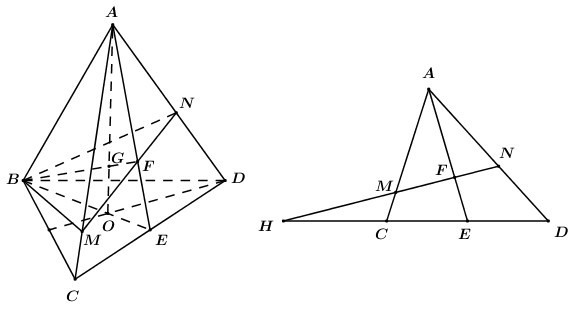
Gọi O là trọng tâm tam giác BCD
\[\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 3\overrightarrow {GO} }\\{ \Rightarrow \overrightarrow {GA} + 3\overrightarrow {GO} = \vec 0}\\{ \Rightarrow \overrightarrow {GA} = - 3\overrightarrow {GO} }\\{ \Rightarrow \frac{{AG}}{{AO}} = \frac{3}{4}}\end{array}\]
Trong (ABE) gọi\[F = BG \cap AE\,\,\left( {F \in AE} \right)\]
Lấy\[M \in AC\] trong (ACD) gọi\[N = MF \cap AD\,\,\,\left( {N \in AD} \right)\] khi đó ta có mặt phẳng chứa BG cắt AC,AD lần lượt tại M,N chính là (BMN).
Áp dụng định lí Menelaus trong tam giác AOE, cát tuyến BGF:
\[\frac{{GA}}{{GO}}.\frac{{BO}}{{BE}}.\frac{{FE}}{{FA}} = 1 \Rightarrow 3.\frac{2}{3}.\frac{{FE}}{{FA}} = 1 \Rightarrow \frac{{FE}}{{FA}} = \frac{1}{2} \Rightarrow \frac{{AF}}{{AE}} = \frac{2}{3} \Rightarrow F\] là trọng tâm tam giác ACD.
Trong (ACD) kéo dài MN cắt CD tại H. Đặt \[\frac{{AM}}{{AC}} = x\left( {0 < x < 1} \right)\]
Áp dụng định lí Menelaus trong tam giác ACE, cát tuyến MHF:\[\frac{{MA}}{{MC}}.\frac{{HC}}{{HE}}.\frac{{FE}}{{FA}} = 1 \Rightarrow \frac{x}{{1 - x}}.\frac{{HC}}{{HE}}.\frac{1}{2} = 1 \Rightarrow \frac{{HC}}{{HE}} = \frac{{2\left( {1 - x} \right)}}{x}\]
\[\begin{array}{*{20}{l}}{ \Rightarrow HE = \frac{x}{{2\left( {1 - x} \right)}}HC}\\{ \Rightarrow HC + CE = \frac{x}{{2\left( {1 - x} \right)}}HC}\\{ \Rightarrow CE = \frac{{3x - 2}}{{2\left( {1 - x} \right)}}HC}\end{array}\]
Ta có:
\[\begin{array}{*{20}{l}}{HD = HC + 2CE}\\{\,\,\,\,\,\,\,\,\, = HC + \frac{{3x - 2}}{{1 - x}}HC = \frac{{2x - 1}}{{1 - x}}HC}\\{ \Rightarrow \frac{{HE}}{{HD}} = \frac{x}{{2\left( {1 - x} \right)}}:\frac{{2x - 1}}{{1 - x}} = \frac{x}{{2\left( {2x - 1} \right)}}}\end{array}\]
Áp dụng định lí Menelaus trong tam giác AED, cát tuyến MFN:
\[\begin{array}{*{20}{l}}{\frac{{FA}}{{FE}}.\frac{{HE}}{{HD}}.\frac{{ND}}{{NA}} = 1 \Rightarrow 2.\frac{x}{{2\left( {2x - 1} \right)}}.\frac{{ND}}{{NA}} = 1}\\{ \Rightarrow \frac{{ND}}{{NA}} = \frac{{2x - 1}}{x} \Rightarrow \frac{{NA}}{{ND}} = \frac{x}{{2x - 1}}}\\{ \Rightarrow \frac{{NA}}{{NA + ND}} = \frac{x}{{x + 2x - 1}} = \frac{x}{{3x - 1}}}\\{ \Rightarrow \frac{{AN}}{{AD}} = \frac{x}{{3x - 1}}}\end{array}\]
Khi đó ta có\[\frac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \frac{{AM}}{{AC}}.\frac{{AN}}{{AD}} = x.\frac{x}{{3x - 1}} = \frac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \frac{1}{3}} \right)\]
Xét hàm số \[f\left( x \right) = \frac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \frac{1}{3}} \right)\] ta có
\[f'\left( x \right) = \frac{{2x\left( {3x - 1} \right) - 3{x^2}}}{{{{\left( {3x - 1} \right)}^2}}} = \frac{{3{x^2} - 2x}}{{{{\left( {3x - 1} \right)}^2}}};f\prime (x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0\,(ktm)}\\{x = \frac{2}{3}}\end{array}} \right.\]
BBT:
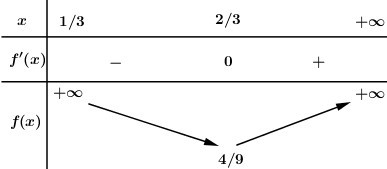
Dựa vào BBT ta thấy\[\mathop {\min }\limits_{\left( {\frac{1}{3}; + \infty } \right)} f\left( x \right) = f\left( {\frac{2}{3}} \right) = \frac{4}{9}\]
Vậy giá trị nhỏ nhất của tỉ số\[\frac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \frac{4}{9}\]
Đáp án cần chọn là: B
Câu 22:
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và có thể tích \[V = \frac{{{a^3}\sqrt 3 }}{6}\]. Tìm số r>0 sao cho tồn tại điểm J nằm trong khối chóp mà khoảng cách từ J đến các mặt bên và mặt đáy đều bằng r?
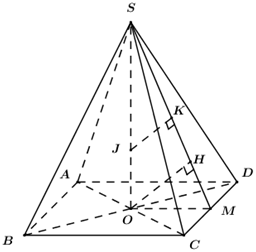
Gọi\[O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\]
Vì khoảng cách từ J đến các mặt bên và mặt đáy đều bằng r nên \[J \in SO.\]
Gọi M là trung điểm của CD, trong (SOM) kẻ \[OH \bot SM\] ta có:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{CD \bot OM}\\{CD \bot SO}\end{array}} \right. \Rightarrow CD \bot (SOM) \Rightarrow CD \bot OH\\\left\{ {\begin{array}{*{20}{c}}{OH \bot CD}\\{OH \bot SM}\end{array}} \right. \Rightarrow OH \bot (SCD)\end{array}\)
Trong (SOM) kẻ\[JK\parallel OH \Rightarrow JK \bot \left( {SCD} \right) \Rightarrow d\left( {J;\left( {SCD} \right)} \right) = JK\]
Có\[d\left( {J;\left( {ABCD} \right)} \right) = JO\]
Theo bài ra ta có\[JK = JO = r\]
Ta có\[{V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} \Rightarrow \frac{{{a^3}\sqrt 3 }}{6} = \frac{1}{3}SO.{a^2} \Rightarrow SO = \frac{{a\sqrt 3 }}{2}\]
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\[OH = \frac{{SO.OM}}{{\sqrt {S{O^2} + O{M^2}} }} = \frac{{\frac{{a\sqrt 3 }}{2}.\frac{a}{2}}}{{\sqrt {\frac{{3{a^2}}}{4} + \frac{{{a^2}}}{4}} }} = \frac{{a\sqrt 3 }}{4}\]
Áp dụng định lí Ta-lét ta có
\[\begin{array}{*{20}{l}}{\frac{{JK}}{{OH}} = \frac{{SJ}}{{SO}} \Rightarrow \frac{r}{{\frac{{a\sqrt 3 }}{4}}} = \frac{{\frac{{a\sqrt 3 }}{2} - r}}{{\frac{{a\sqrt 3 }}{2}}}}\\{ \Leftrightarrow 2r = \frac{{a\sqrt 3 }}{2} - r}\\{ \Leftrightarrow 3r = \frac{{a\sqrt 3 }}{2} \Leftrightarrow r = \frac{{a\sqrt 3 }}{6}}\end{array}\]
Đáp án cần chọn là: D
Câu 23:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N lần lượt là trung điểm của các cạnh AB,BC. Điểm I thuộc đoạn SA. Biết mặt phẳng (MNI) chia khối chóp S.ABCD thành hai phần, phần chứa đỉnh S có thể tích bằng \[\frac{7}{{25}}\] lần phần còn lại. Tính tỉ số \[\frac{{IA}}{{IS}}\]?
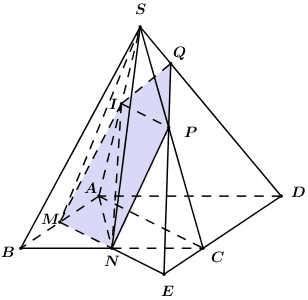
Giả sử\[SC \cap \left( {IMN} \right) = \left\{ P \right\} \Rightarrow \left( {IMN} \right) \cap \left( {SAC} \right) = IP\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{(IMN) \cap (SAC) = IP}\\{(IMN) \cap (ABCD) = MN}\\{(SAC) \cap (ABCD) = AC}\end{array}} \right. \Rightarrow IP\parallel MN\parallel AC\)
Trong (ABCD) gọi \[\left\{ E \right\} = MN \cap CD\]trong (SCD) gọi \[Q = NP \cap SD\]
Khi đó thiết diện của hình chóp cắt bởi (MNI) là ngũ giác IMNPQ.
Gọi\[SM \cap \left( {ABCD} \right) = E \Rightarrow \frac{{d\left( {M;\left( {ABCD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}} = \frac{{ME}}{{SE}} = \frac{{11}}{{35}}\]theo bài ra ta có\[\frac{{{V_2}}}{{{V_1}}} = \frac{{{V_{M.ACD}}}}{{{V_{S.ABCD}}}} = \frac{{\frac{1}{3}.d\left( {M;\left( {ABCD} \right)} \right).{S_{ACD}}}}{{\frac{1}{3}.d\left( {S;\left( {ABCD} \right)} \right).{S_{ABCD}}}} = \frac{{11}}{{35}}.\frac{1}{2} = \frac{{11}}{{70}}\]
Ta có \[{V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\]
Đặt\[\frac{{SI}}{{SA}} = x\,\,\,(0 < x < 1)\]áp dụng định lí Ta-lét ta có\[\frac{{SI}}{{SA}} = \frac{{SP}}{{SC}} = x\]
- Xét khối chóp S.BMN và S.ABCD:
+ Có cùng chiều cao (cùng bằng khoảng cách từ SS đến (ABCD).
\[{S_{BMN}} = \frac{1}{4}{S_{ABC}} = \frac{1}{8}{S_{ABC}}\](do tam giác BMNBMN và tam giác BACBAC đồng dạng theo tỉ số\[DH \bot \left( {ABC} \right)\])
Do đó\[{V_{S.BMN}} = \frac{1}{8}{V_{S.ABCD}} = \frac{1}{8}V\]
- Xét khối chóp S.IMN và S.AMN:
\[\frac{{{V_{S.IMN}}}}{{{V_{S.AMN}}}} = \frac{{SI}}{{SA}} = x \Rightarrow {V_{S.IMN}} = x.{V_{S.AMN}}\]
Ta có\[{S_{AMN}} = {S_{BMN}} = \frac{1}{8}{S_{ABCD}} \Rightarrow {V_{S.AMN}} = \frac{1}{8}V \Rightarrow {V_{S.IMN}} = \frac{x}{8}V\]
- Xét khối chóp S.INP và S.ANC:
\[\frac{{{V_{S.INP}}}}{{{V_{S.ANC}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}} = {x^2} \Rightarrow {V_{S.IMN}} = {x^2}.{V_{S.ANC}}\]
Ta có\[{S_{ANC}} = \frac{1}{2}{S_{ABC}} = \frac{1}{4}{S_{ABCD}} \Rightarrow {V_{S.ANC}} = \frac{1}{4}V \Rightarrow {V_{S.IMN}} = \frac{{{x^2}}}{4}V\]
- Xét khối chóp S.IPQ và S.ACD:\[\frac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}}\]
Ta có AMEC là hình bình hành nên\[EC = AM = \frac{1}{2}CD \Rightarrow \frac{{EC}}{{ED}} = \frac{1}{3}\]
Áp dụng định lí Menelaus trong tam giác SCD với cát tuyến EPQ ta có:
\[\frac{{PS}}{{PC}}.\frac{{EC}}{{ED}}.\frac{{QD}}{{QS}} = 1 \Rightarrow \frac{x}{{1 - x}}.\frac{1}{3}.\frac{{QD}}{{QS}} = 1\]
\[\begin{array}{*{20}{l}}{ \Rightarrow \frac{{QD}}{{QS}} = \frac{{3\left( {1 - x} \right)}}{x} \Rightarrow \frac{{SQ}}{{QD}} = \frac{x}{{3\left( {1 - x} \right)}}}\\{ \Rightarrow \frac{{SQ}}{{SQ + QD}} = \frac{x}{{x + 3\left( {1 - x} \right)}}}\\{ \Rightarrow \frac{{SQ}}{{SD}} = \frac{x}{{3 - 2x}}}\end{array}\]
Suy ra\[\frac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \frac{{SI}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}} = {x^2}.\frac{x}{{3 - 2x}} = \frac{{{x^3}}}{{3 - 2x}}\]
\[ \Rightarrow {V_{S.IPQ}} = \frac{{{x^3}}}{{3 - 2x}}{V_{S.ACD}}\]
Mà\[{S_{ACD}} = \frac{1}{2}{S_{ABCD}} \Rightarrow {V_{S.ACD}} = \frac{1}{2}V \Rightarrow {V_{S.IPQ}} = \frac{{{x^3}}}{{2\left( {3 - 2x} \right)}}V\]
Khi đó ta có:
\[{V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\]
\[ \Rightarrow {V_1} = \frac{1}{8}V + \frac{x}{8}V + \frac{{{x^2}}}{4}V + \frac{{{x^3}}}{{2(3 - 2x)}}V\]
\[\begin{array}{l} \Rightarrow {V_1} = \left( {\frac{1}{8} + \frac{x}{8} + \frac{{{x^2}}}{4} + \frac{{{x^3}}}{{2(3 - 2x)}}} \right)V = \frac{7}{{32}}V\\ \Rightarrow \frac{1}{8} + \frac{x}{8} + \frac{{{x^2}}}{4} + \frac{{{x^3}}}{{2(3 - 2x)}} = \frac{7}{{32}}\\ \Leftrightarrow \frac{{1 + x + 2x2}}{4} + \frac{{{x^3}}}{{3 - 2x}} = \frac{7}{{16}}\\ \Leftrightarrow (1 + x + 2{x^2}).(12 - 8x) + 16{x^3} = 7(3 - 2x)\\ \Leftrightarrow 12 + 12x + 24{x^2} - 8x - 8{x^2} - 16{x^3} + 16{x^3} = 21 - 14x\\ \Leftrightarrow 16{x^2} + 18x - 9 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{3}{8}\left( {tm} \right)}\\{x = - \frac{3}{2}\left( {ktm} \right)}\end{array}} \right.\end{array}\]
\[ \Rightarrow \frac{{SI}}{{SA}} = \frac{3}{8} \Rightarrow \frac{{IS}}{{IA}} = \frac{3}{5} \Rightarrow \frac{{IA}}{{IS}} = \frac{5}{3}\]
Đáp án cần chọn là: A
Câu 24:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp S.ABC
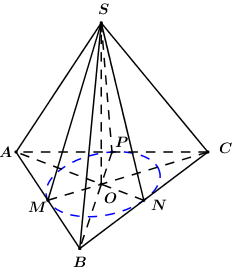
Gọi M,N,P lần lượt là hình chiếu của điểm SS lên AB,BC,AC ta có:
\[\begin{array}{*{20}{l}}{\,\,\,\,\,{S_{{\rm{\Delta }}ABC}} = {S_{{\rm{\Delta }}BCA}} = {S_{{\rm{\Delta }}CAB}}}\\{ \Rightarrow \frac{1}{2}SM.AB = \frac{1}{2}SN.BC = \frac{1}{2}SP.CA}\end{array}\]
Mà\[AB = BC = CA\,\,\left( {gt} \right) \Rightarrow SM = SN = SP\]
Gọi O là hình chiếu của S lên (ABC), ta có:
\(\left\{ {\begin{array}{*{20}{c}}{AB \bot SM}\\{AB \bot SO}\end{array}} \right. \Rightarrow AB \bot (SOM) \Rightarrow AB \bot OM\)
CMTT ta có\[ON \bot BC,\,\,OP \bot AC\]
Xét các tam giác vuông\[{\rm{\Delta }}SOM,\,\,{\rm{\Delta }}SON,\,\,{\rm{\Delta }}SOP\]có:
\[\begin{array}{*{20}{l}}{SO\,\,chung}\\{SM = SN = SP\,\,\left( {cmt} \right)}\end{array}\]
\[ \Rightarrow {\rm{\Delta }}SOM = {\rm{\Delta }}SON = {\rm{\Delta }}SOP\](cạnh huyền – cạnh góc vuông)
\[ \Rightarrow OM = ON = OP\] suy ra O cách đều các cạnh AB,BC,CA nên OO là tâm đường tròn nội tiếp \[{\rm{\Delta }}ABC\]hoặc O là tâm đường tròn bàng tiếp\[{\rm{\Delta }}ABC\]
+ TH1: O là tâm đường tròn nội tiếp\[{\rm{\Delta }}ABC\] Mà\[{\rm{\Delta }}ABC\]đều nên O là đồng thời là trọng tâm tam giác đều ABC. Khi đó ta có
\[AN = \frac{{\sqrt 6 .\sqrt 3 }}{2} = \frac{{3\sqrt 2 }}{2},\,\,AO = \frac{2}{3}AN = \sqrt 2 \]
\[ \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {18 - 2} = 4\]
\[{S_{{\rm{\Delta }}ABC}} = {\left( {\sqrt 6 } \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{2}\]
\[ \Rightarrow {V_{S.ABC}} = \frac{1}{3}SO.{S_{{\rm{\Delta }}ABC}} = \frac{1}{3}.4.\frac{{3\sqrt 3 }}{2} = 2\sqrt 3 \]
TH2: O là tâm đường tròn bàng tiếp \[\Delta ABC\].
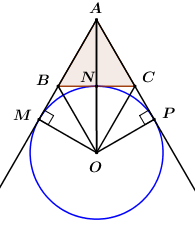
Gọi R là bán kính đường tròn bàng tiếp tam giác ABC, p là nửa chu vi tam giác ABC
\[ \Rightarrow p = \frac{{3\sqrt 6 }}{2}\]
Khi đó ta có\[{S_{ABC}} = \left( {p - BC} \right).R\]
\[ \Rightarrow {\left( {\sqrt 6 } \right)^2}.\frac{{\sqrt 3 }}{4} = \left( {\frac{{3\sqrt 6 }}{2} - \sqrt 6 } \right).R \Leftrightarrow R = \frac{{3\sqrt 2 }}{2}\]
Có\[AN = \frac{{\sqrt 6 .\sqrt 3 }}{2} = \frac{{3\sqrt 2 }}{2} \Rightarrow OA = AN + ON = 3\sqrt 2 \]
\[ \Rightarrow SA > OA = 3\sqrt 2 \] (quan hệ giữa đường vuông góc và đường xiên)
\[ \Rightarrow SB = 3\sqrt 2 \]
Áp dụng định lí Pytago trong tam giác vuông OBM có:
\[OB = \sqrt {O{M^2} + B{M^2}} = \sqrt {{{\left( {\frac{{3\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 6 }}{2}} \right)}^2}} = \sqrt 6 \]
Áp dụng định lí Pytago trong tam giác vuông SOB có:
\[SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {{{\left( {3\sqrt 2 } \right)}^2} - {{\left( {\sqrt 6 } \right)}^2}} = 2\sqrt 3 \]
Khi đó ta có\[{V_{S.ABC}} = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.2\sqrt 3 .{\left( {\sqrt 6 } \right)^2}.\frac{{\sqrt 3 }}{4} = 3\]
Vậy\[\min {V_{S.ABC}} = 3\]
Đáp án cần chọn là: A
Câu 25:
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy góc 600. Thể tích của khối chóp đó là:
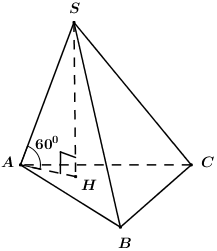
Xét tam giác ABC, giả sử \[AB = 6,\,\,BC = 8,\,\,AC = 10\] ta có\[A{B^2} + B{C^2} = A{C^2}\,\,\left( { = 100} \right)\] nên tam giác ABC vuông tại B (định lí Pytago đảo)
\[ \Rightarrow {S_{{\rm{\Delta }}ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}.6.8 = 24\]
Gọi H là hình chiếu vuông góc của S lên (ABC) và giả sử SA hợp với đáy góc 600 ⇒HA là hình chiếu của SA lên (ABC) nên
\[\angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;HA} \right) = \angle SAH = {60^0}\]
\[ \Rightarrow SH = SA.\sin {60^0} = 4.\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \]
Vậy\[{V_{S.ABC}} = \frac{1}{3}SH.{S_{{\rm{\Delta }}ABC}} = \frac{1}{3}.2\sqrt 3 .24 = 16\sqrt 3 \]
Đáp án cần chọn là: DCâu 26:
Nếu một khối chóp có thể tích bằng a3 và diện tích mặt đáy bằng a2 thì chiều cao của khối chóp bằng:
Chiều cao của khối chóp đã cho là:
\[h = \frac{{3V}}{S} = \frac{{3{a^3}}}{{{a^2}}} = 3a.\]
Đáp án cần chọn là: B
Câu 27:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD song song với BC, AD=2BC. Gọi E, F là hai điểm lần lượt nằm trên các cạnh AB và AD sao cho \[\frac{{3AB}}{{AE}} + \frac{{AD}}{{AF}} = 5\;\] (E,F không trùng với A), Tổng giá trị lớn nhất và giá trị nhỏ nhất của tỉ số thể tích hai khối chóp S.BCDFE và S.ABCD là:
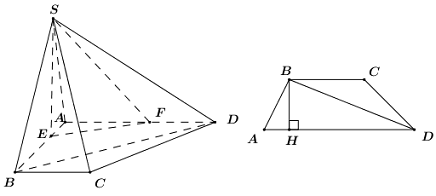
Đặt \[\frac{{AE}}{{AB}} = x,\,\,\frac{{AF}}{{AD}} = y\,\,(0 < x,\,\,y \le 1)\]Theo bài ra ta có\[\frac{{3AB}}{{AE}} + \frac{{AD}}{{AF}} = 5\]
\[ \Rightarrow \frac{3}{x} + \frac{1}{y} = 5\,\,\,\left( 1 \right)\]
Vì hai khối chóp S.BCDFE và S.ABCD có cùng chiều cao nên
\[k = \frac{{{V_{S.BCDFE}}}}{{{V_{S.ABCD}}}} = \frac{{{S_{BCDFE}}}}{{{S_{ABCD}}}}\]
Đặt\[{S_{ABCD}} = S\] kẻ\[BH \bot AD\,\,\left( {H \in AD} \right)\]ta có
\[S = \frac{1}{2}BH.\left( {BC + AD} \right) = \frac{3}{2}.BH.BC\]
Ta có:\[\frac{{{S_{AEF}}}}{{{S_{ABD}}}} = \frac{{\frac{1}{2}AE.AF.\sin \angle BAD}}{{\frac{1}{2}AB.AD.\sin \angle BAD}} = xy \Rightarrow {S_{AEF}} = xy.{S_{ABD}}\]
Mà\[{S_{ABD}} = \frac{1}{2}BH.AD\]nên
\[{S_{AEF}} = \frac{1}{2}xy.BH.AD = xy.BH.BC = \frac{3}{2}BH.BC.\frac{2}{3}xy \Rightarrow {S_{AEF}} = \frac{2}{3}xy.S\]
\[ \Rightarrow {S_{BCDFE}} = {S_{ABCD}} - {S_{AEF}} = S - \frac{2}{3}xy.S = S\left( {1 - \frac{2}{3}xy} \right)\]
\[ \Rightarrow k = \frac{{S.\left( {1 - \frac{2}{3}xy} \right)}}{S} = 1 - \frac{2}{3}xy\]
Theo (1) ta có:\[\frac{3}{x} + \frac{1}{y} = 5 \Leftrightarrow y = \frac{x}{{5x - 3}}\]
Ta có
\[0 < \frac{x}{{5x - 3}} \le 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{x}{{5x - 3}} > 0}\\{\frac{{x - 5x + 3}}{{5x - 3}} \le 0}\end{array}} \right.\]</>
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5x - 3 > 0\,(do\,\,x > 0)}\\{3 - 4x \le 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > \frac{3}{5}}\\{x \ge \frac{3}{4}}\end{array}} \right. \Leftrightarrow x \ge \frac{3}{4}\)
Khi đó ta có
\[\begin{array}{*{20}{l}}{k = 1 - \frac{2}{3}xy = 1 - \frac{2}{3}x.\frac{x}{{5x - 3}}}\\{\,\,\,\, = 1 - \frac{{2{x^2}}}{{3\left( {5x - 3} \right)}} = \frac{{15x - 9 - 2{x^2}}}{{3\left( {5x - 3} \right)}} = f\left( x \right)}\end{array}\]
Xét hàm số\[f\left( x \right) = \frac{{ - 2{x^2} + 15x - 9}}{{3\left( {5x - 3} \right)}}\]với \[\frac{3}{4} \le x \le 1\]ta có:
\[f\prime (x) = {\frac{{( - 4x + 15).3(5x - 3) - ( - 2{x^2} + 15x - 9).15}}{{9{{(5x - 3)}^2}}}^{}}\]
\[f\prime (x) = \frac{{3( - 20{x^2} + 87x - 45) - ( - 30{x^2} + 225x - 135)}}{{9{{(5x - 3)}^2}}}\]
\[f\prime (x) = \frac{{ - 30{x^2} + 36x}}{{9{{(5x - 3)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{6}{5}\left( {ktm} \right)}\\{x = 0\left( {ktm} \right)}\end{array}} \right.\]
BBT:
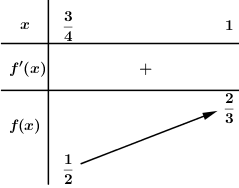
\[ \Rightarrow {k_{\min }} = \frac{1}{2},\,\,{k_{\max }} = \frac{2}{3}\]
Vậy\[{k_{\min }} + {k_{\max }} = \frac{1}{2} + \frac{2}{3} = \frac{7}{6}\]
Đáp án cần chọn là: D
Câu 28:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,BC=2AB=2a. Cạnh bên SC vuông góc với đáy, góc giữa SA và đáy bằng 600. Thể tích khối chóp đó bằng:
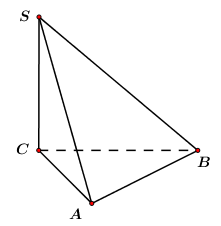
Áp dụng định lý Pitago cho \[\Delta ABC\] vuông tại A ta có:
\[AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 .\]
\[ \Rightarrow {S_{{\rm{\Delta }}ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.a.a\sqrt 3 = \frac{{{a^2}\sqrt 3 }}{2}.\]
Ta có:\[SC \bot \left( {ABC} \right) \Rightarrow SC \bot AC\]
⇒AC là hình chiếu của SA trên (ABC)
\[ \Rightarrow \angle \left( {SA,\,\,\left( {ABC} \right)} \right) = \angle \left( {SA,\,\,AC} \right) = \angle SAC = {60^0}\]
Xét \[{\rm{\Delta }}SAC\] vuông tại C ta có: \[SC = CA.\tan {60^0} = a\sqrt 3 .\sqrt 3 = 3a.\]
\[ \Rightarrow {V_{S.ABC}} = \frac{1}{3}SC.{S_{{\rm{\Delta }}ABC}} = \frac{1}{3}.3a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}.\]

Đáp án cần chọn là: D
Câu 29:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng 2, \[\angle BAD = {60^0}\], SA=SC và tam giác SBD vuông cân tại S. Gọi E là trung điểm của SC. Mặt phẳng (P) qua AE và cắt hai cạnh SB,SD lần lượt tại M và N. Thể tích lớn nhất V0 của khối đa diện ABCDNEM bằng:
Gọi\[O = AC \cap BD\]ta có:
\[SA = SC \Rightarrow {\rm{\Delta }}SAC\]cân tại \[S \Rightarrow SO \bot AC\]
Tam giác SBD vuông cân tại\[S \Rightarrow SO \bot BD\]
\[ \Rightarrow SO \bot \left( {ABCD} \right)\]
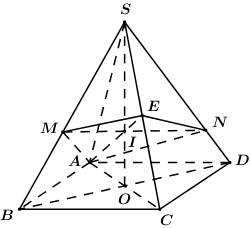
Trong (SBD), gọi\[I = MN \cap BD\]
Đặt \[\frac{{SM}}{{SB}} = x,\,\,\frac{{SN}}{{SD}} = y\,\,(0 < x,\,\,y < 1)\]
Ta có:\[\frac{{{V_{S.AME}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SB}}.\frac{{SE}}{{SC}} = \frac{1}{2}x \Rightarrow \frac{{{V_{S.AME}}}}{{{V_{S.ABCD}}}} = \frac{1}{4}x\]
\[\frac{{{V_{S.ANE}}}}{{{V_{S.ADC}}}} = \frac{{SN}}{{SD}}.\frac{{SE}}{{SC}} = \frac{1}{2}y \Rightarrow \frac{{{V_{S.ANE}}}}{{{V_{S.ABCD}}}} = \frac{1}{4}y\]
\[ \Rightarrow \frac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \frac{{{V_{S.AME}}}}{{{V_{S.ABCD}}}} + \frac{{{V_{S.ANE}}}}{{{V_{S.ABCD}}}} = \frac{{x + y}}{4}\,\,\,\left( 1 \right)\]
Ta lại có:\[\frac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SD}} = xy \Rightarrow \frac{{{V_{S.AMN}}}}{{{V_{S.ABCD}}}} = \frac{{xy}}{2}\]
\[\frac{{{V_{S.MNE}}}}{{{V_{S.BDC}}}} = \frac{{SM}}{{SB}}.\frac{{SN}}{{SD}}.\frac{{SE}}{{SC}} = \frac{1}{2}xy \Rightarrow \frac{{{V_{S.MNE}}}}{{{V_{S.ABCC}}}} = \frac{{xy}}{4}\]
\[ \Rightarrow \frac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \frac{{{V_{S.AMN}}}}{{{V_{S.ABCD}}}} + \frac{{{V_{S.MNE}}}}{{{V_{S.ABCD}}}} = \frac{{xy}}{2} + \frac{{xy}}{4} = \frac{{3xy}}{4}\,\,\left( 2 \right)\]
Từ (1) và (2) \[ \Rightarrow \frac{{x + y}}{4} = \frac{{3xy}}{4} \Leftrightarrow x + y = 3xy\]
\[ \Leftrightarrow x = \left( {3x - 1} \right)y \Leftrightarrow y = \frac{x}{{3x - 1}}\,\,\left( {x \ne \frac{1}{3}} \right)\]
Do \[x,\,\,y > 0 \Rightarrow 3x - 1 > 0 \Leftrightarrow x > \frac{1}{3}\]
Khi đó ta có\[\frac{{{V_{S.AMNE}}}}{{{V_{S.ABCD}}}} = \frac{1}{4}\left( {x + \frac{x}{{3x - 1}}} \right)\]
Xét hàm số \[f\left( x \right) = x + \frac{x}{{3x - 1}}\,\,\left( {x > \frac{1}{3}} \right)\]ta có:
\[f'\left( x \right) = 1 - \frac{1}{{{{\left( {3x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x - 1 = 1}\\{3x - 1 = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{2}{3}}\\{x = 0\left( {ktm} \right)}\end{array}} \right.\]
BBT:
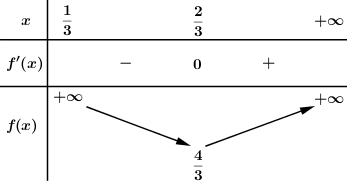
Dựa vào BBT ta thấy\[\min {V_{S.AMNE}} = \frac{1}{4}.\frac{4}{3}{V_{S.ABCD}} = \frac{1}{3}{V_{S.ABCD}}\]
\[ \Rightarrow \max {V_{ABCDNEM}} = \frac{2}{3}{V_{S.ABCD}} \Rightarrow {V_0} = \frac{2}{3}{V_{S.ABCD}}\]
Ta có: \[{\rm{\Delta }}ABD\]đều cạnh 2 \[\left( {AB = AD,\,\angle BAD = {{60}^0}} \right) \Rightarrow {S_{ABD}} = \frac{{{2^2}\sqrt 3 }}{4} = \sqrt 3 \]
\[ \Rightarrow {S_{ABCD}} = 2\sqrt 3 \]
Tam giác ABD đều cạnh 2 ⇒BD=2, lại có tam giác SBD vuông cân tại S nên
\[SO = \frac{1}{2}BD = 1\]
\[ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.1.2\sqrt 3 = \frac{{2\sqrt 3 }}{3}\]
Vậy\[{V_0} = \frac{2}{3}{V_{S.ABCD}} = \frac{{4\sqrt 3 }}{9}\]Đáp án cần chọn là: D
Câu 30:
Khối chóp có đáy là hình bình hành, một cạnh đáy bằng a và các cạnh bên đều bằng \(a\sqrt 2 \). Thể tích của khối chóp có giá trị lớn nhất là:
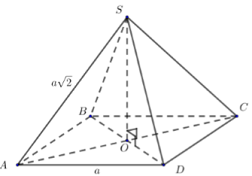
Gọi \[O = AC \cap BD\]
Tam giác SAC cân tại S, SO là trung tuyến\[ \Rightarrow SO \bot AC\]
Tam giác SBD cân tại S, SO là trung tuyến \[ \Rightarrow SO \bot BD\]
\[ \Rightarrow SO \bot \left( {ABCD} \right)\]
Vì \[SA = SB = SC = SDSO \bot \left( {ABCD} \right)\] nên O là tâm đường tròn ngoại tiếp ABCD.
Hình bình hành ABCD nội tiếp đường tròn (O) nên ABCD phải là hình chữ nhật.
Theo bài ra ta giả sử AD=a và đặt\[AB = x\,\,\left( {x > 0} \right)\]
Áp dụng định lí Pytago trong tam giác vuông ABC có:
\[AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {x^2}} \]
\[ \Rightarrow AO = \frac{1}{2}AC = \frac{1}{2}\sqrt {{a^2} + {x^2}} \]
Áp dụng định lí Pytago trong tam giác vuông SOA có:
\[SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {2{a^2} - \frac{{{a^2} + {x^2}}}{4}} = \frac{1}{2}\sqrt {7{a^2} - {x^2}} \]
Khi đó ta có
\[{V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{1}{2}\sqrt {7{a^2} - {x^2}} .ax = \frac{a}{6}x\sqrt {7{a^2} - {x^2}} \]
Áp dụng BĐT Cô-si ta có:\[x\sqrt {7{a^2} - {x^2}} \le \frac{{{x^2} + 7{a^2} - {x^2}}}{2} = \frac{{7{a^2}}}{2}\]
\[ \Rightarrow {V_{S.ABCD}} \le \frac{a}{6}.\frac{{7{a^2}}}{2} = \frac{{7{a^3}}}{{12}}\]
Dấu “=” xảy ra \[ \Leftrightarrow {x^2} = 7{a^2} - {x^2} \Leftrightarrow x = \frac{{a\sqrt {14} }}{2}\]
Vậy thể tích khối chóp S.ABCD đạt giá trị lớn nhất bằng\[\frac{{7{a^3}}}{{12}} \Leftrightarrow x = \frac{{a\sqrt {14} }}{2}\]
Đáp án cần chọn là: D
Câu 31:
Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là a,2a,3a có thể tích lớn nhất bằng
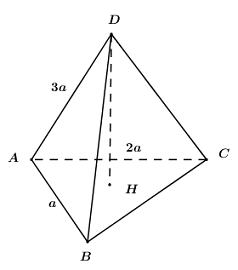
Giả sử khối chóp ABCD có \[AB = a,\,\,AC = 2a,\,\,AD = 3a\]
Gọi H là hình chiếu vuông góc của D lên (ABC), khi đó ta có:\[DH \bot \left( {ABC} \right)\] và\[DH \le AD\]
Ta có: \[{S_{ABC}} = \frac{1}{2}AB.AC.\sin \angle BAC \le \frac{1}{2}AB.AC\]
Vây\[{V_{ABCD}} = \frac{1}{3}DH.{S_{{\rm{\Delta }}ABC}} \le \frac{1}{3}AD.\frac{1}{2}AB.AC = \frac{1}{6}AB.AC.AD = \frac{1}{6}.a.2a.3a = {a^3}\]
Dấu “=” xảy ra\[ \Leftrightarrow AD \bot \left( {ABC} \right),\,\,AB \bot AC\] hay AB,AC,AD đôi một vuông góc.
Đáp án cần chọn là: D
Câu 32:
Cho hình chóp S.ABC, đáy là tam giác ABC có \[AB = BC\sqrt 5 ,\;AC = 2BC\sqrt 2 \], hình chiếu của S lên mặt phẳng (ABC) là trung điểm O của cạnh AC. Khoảng cách từ A đến mặt phẳng (SBC) bằng 2. Mặt phẳng (SBC) hợp với mặt phẳng (ABC) một góc α thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp S.ABC bằng \(\frac{{\sqrt a }}{b}\), trong đó \[a,b \in {\mathbb{N}^*},\;\]a là số nguyên tố. Tổng a+b bằng:
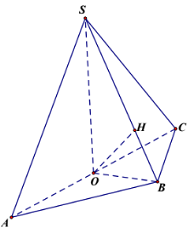
Gọi H là hình chiếu của O lên SB.
Ta có:\[OB = \sqrt {\frac{{2B{C^2} + 2B{A^2} - A{C^2}}}{4}} = BC,OC = \frac{1}{2}AC = BC\sqrt 2 \]
Suy ra\[OB \bot BC\]
Dễ thấy\[\angle SBO = \alpha \]và\[OH = d\left( {O;\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = 1\]
Suy ra\[SO = \frac{{OH}}{{\cos \alpha }} = \frac{1}{{\cos \alpha }},OB = \frac{{OH}}{{\sin \alpha }} = \frac{1}{{\sin \alpha }}\]
\[ \Rightarrow BC = OB = \frac{1}{{\sin \alpha }}\]
Thể tích khối chóp S.ABC là:
\[\begin{array}{*{20}{l}}{{V_{S.ABC}} = \frac{1}{3}SO.{S_{ABC}} = \frac{1}{3}SO.2{S_{OBC}}}\\{\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{3}.\frac{1}{{\cos \alpha }}.{{\left( {\frac{1}{{\sin \alpha }}} \right)}^2} = \frac{1}{{3\cos \alpha .{{\sin }^2}\alpha }}}\end{array}\]
Áp dụng bất đẳng thức Cô-si ta có:
\[\begin{array}{*{20}{l}}{1 = \frac{1}{2}{{\sin }^2}\alpha + \frac{1}{2}{{\sin }^2}\alpha + {{\cos }^2}\alpha \ge 3.\sqrt[3]{{\frac{1}{4}{{\sin }^4}\alpha .{{\cos }^2}\alpha }}}\\{ \Leftrightarrow \frac{1}{{27}} \ge \frac{1}{4}.si{n^4}\alpha .co{s^2}\alpha \Rightarrow \frac{1}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} \ge \frac{{3\sqrt 3 }}{2}}\\{ \Rightarrow {V_{S.ABC}} \ge \frac{{\sqrt 3 }}{2}}\end{array}\]
Vậy\[\min {V_{S.ABC}} = \frac{{\sqrt 3 }}{2}\].Dấu “=” xảy ra\[ \Leftrightarrow {\cos ^2}\alpha = \frac{1}{2}{\sin ^2}\alpha = \frac{1}{3} \Leftrightarrow \cos \alpha = \frac{{\sqrt 3 }}{3}\]
\[ \Rightarrow a = 3,\,\,b = 2\]
Vậy\[a + b = 3 + 2 = 5\]
Đáp án cần chọn là: B
Câu 33:
Cho khối chóp S.ABCD có thể tích bằng 4a3, đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng a2. Tính khoảng cách từ M tới mặt phẳng (SAB).
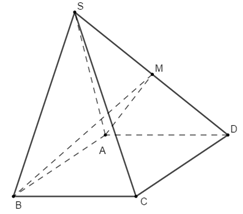
Vì M là trung điểm của SD nên \[\frac{{{V_{SABM}}}}{{{V_{SABD}}}} = \frac{{SM}}{{SD}} = \frac{1}{2}\]
Mà\[\frac{{{V_{SABD}}}}{{{V_{SABCD}}}} = \frac{1}{2} \Rightarrow {V_{SABD}} = \frac{1}{2}.4{a^3} = 2{a^3}\]
\[ \Rightarrow {V_{SABM}} = {a^3} = \frac{1}{3}.d\left( {M;\left( {SAB} \right)} \right).{S_{SAB}} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \frac{{3{a^3}}}{{{a^2}}} = 3a\]
Đáp án cần chọn là: C