Bài toán về điểm biểu diễn số phức trong mặt
-
325 lượt thi
-
34 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm điểm M biểu diễn số phức \[z = i - 2\]
\[z = i - 2 = - 2 + i\] nên điểm biểu diễn là M(−2;1)
Đáp án cần chọn là: C
Câu 2:
Cho số phức z thỏa mãn \[(1 + i)z = 3 - i\]. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình bên ?
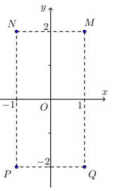
\[\left( {1 + i} \right)z = 3 - i \Rightarrow z = \frac{{3 - i}}{{1 + i}} = \frac{{\left( {3 - i} \right)\left( {1 - i} \right)}}{{\left( {1 + i} \right)\left( {1 - i} \right)}} = \frac{{2 - 4i}}{{{1^2} + {1^2}}} = 1 - 2i \Rightarrow Q\left( {1; - 2} \right)\]
là điểm biểu diễn z.
Đáp án cần chọn là: B
Câu 3:
Cho số phức \[z = 2 + 5i\]. Tìm số phức \[w = iz + \overline z \]
Đáp án cần chọn là: B
Câu 4:
Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện \[\left| {z - i} \right| = 5\] và \[{z^2}\] là số thuần ảo?
Đặt\[z = a + bi\]
Ta có:\[\left| {z - i} \right| = 5 \Leftrightarrow \left| {a + bi - i} \right| = 5\]
\[ \Leftrightarrow \left| {a + \left( {b - 1} \right)i} \right| = 5 \Leftrightarrow \sqrt {{a^2} + {{\left( {b - 1} \right)}^2}} = 5 \Leftrightarrow {a^2} + {\left( {b - 1} \right)^2} = 25\]
\[{z^2} = {(a + bi)^2} = {a^2} + 2{\rm{a}}bi - {b^2} = {a^2} - {b^2} + 2abi\]
Do\[{z^2}\] là số thuần ảo nên:\[{a^2} - {b^2} = 0 \Leftrightarrow (a - b)(a + b) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{b = a}\\{b = - a}\end{array}} \right.\]
TH1: b=a thay vào (1) ta được:
\[{a^2} + {\left( {a - 1} \right)^2} = 25 \Leftrightarrow {a^2} + {a^2} - 2a + 1 = 25 \Leftrightarrow 2{a^2} - 2a - 24 = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a = 4 \Rightarrow b = 4}\\{a = - 3 \Rightarrow b = - 3}\end{array}} \right.\)
TH2: b=-a thay vào (1) ta được:
\[{a^2} + {\left( { - a - 1} \right)^2} = 25 \Leftrightarrow {a^2} + {a^2} + 2a + 1 = 25 \Leftrightarrow 2{a^2} + 2a - 24 = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a = 3 \Rightarrow b = - 3}\\{a = - 4 \Rightarrow b = 4}\end{array}} \right.\)
Vậy có 4 số phức cần tìm là:\[4 + 4i, - 3 - 3i,3 - 3i, - 4 + 4i\]
Đáp án cần chọn là: C
Câu 5:
Cho số phức z thỏa mãn (2−i)z=7−i . Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình dưới.
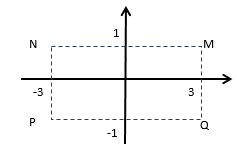
\[\left( {2 - i} \right)z = 7 - i \Rightarrow z = \frac{{7 - i}}{{2 - i}} = \frac{{(7 - i)(2 + i)}}{5} = \frac{{15 + 5i}}{5} = 3 + i\]
Suy ra điểm có tọa độ (3;1) sẽ biểu diễn số phức z, suy ra M thỏa mãn.
Đáp án cần chọn là: C
Câu 6:
Trên mặt phẳng tọa độ, điểm M là điểm biểu diển của số phức z (như hình vẽ bên). Điểm nào trong hình vẽ là điểm biểu diển của số phức 2z?
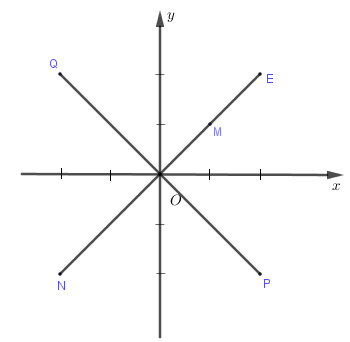
Điểm M(1;1) biểu diễn số phức\[z = 1 + i \Rightarrow 2z = 2 + 2i\]
Do đó điểm biểu diễn số phức 2z là (2;2) (điểm E).
Đáp án cần chọn là: C
Câu 7:
Số phức z thỏa mãn \[\left| z \right| + z = 0\]. Khi đó:
Đặt\[z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \]
Ta có:\[\left| z \right| + z = 0 \Leftrightarrow \sqrt {{a^2} + {b^2}} + a + bi = 0 + 0i\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{b = 0}\\{\sqrt {{a^2} + {b^2}} + a = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{b = 0}\\{|a| + a = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{b = 0}\\{a \le 0}\end{array}} \right.\)
Đáp án cần chọn là: C
Câu 8:
Cho ba điểm A,B,C lần lượt biểu diễn các số phức sau \[{z_1} = 1 + i;{z_2} = z_1^2;{z_3} = m - i\]. Tìm các giá trị thực của m sao cho tam giác ABC vuông tại B.
Ta có:\[{z_2} = 2i\]
Có A(1;1);B(0;2) và C(m;−1)
\[\overrightarrow {AB} = ( - 1;1);\overrightarrow {BC} = (m; - 3) \Rightarrow \overrightarrow {AB} .\overrightarrow {BC} = - 1.m - 3 = 0 \Leftrightarrow m = - 3\]
Đáp án cần chọn là: A
Câu 9:
Cho số phức z thỏa mãn \(\left| z \right| = \frac{{\sqrt 2 }}{2}\)và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức \[{\rm{w}} = \frac{1}{{iz}}\] là một trong bốn điểm M,N,P,Q. Khi đó điểm biểu diễn của số phức w là
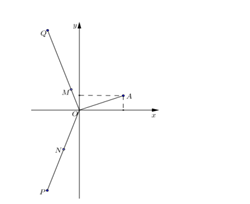
Do điểm A là điểm biểu diễn của z nằm trong góc phần tư thứ nhất của mặt phẳng Oxy nên gọi\[z = a + bi\left( {a,b > 0} \right)\]
Do \[\left| z \right| = \frac{{\sqrt 2 }}{2} \Rightarrow \sqrt {{a^2} + {b^2}} = \frac{{\sqrt 2 }}{2}\]
Lại có:\[{\rm{w}} = \frac{1}{{iz}} = \frac{{ - b}}{{{a^2} + {b^2}}} - \frac{a}{{{a^2} + {b^2}}}i\]
\[\left| {\rm{w}} \right| = \left| {\frac{1}{{iz}}} \right| = \frac{1}{{\left| i \right|.\left| z \right|}} = \sqrt 2 = 2\left| z \right| = 2OA\]
Vậy điểm biểu diễn của số phức w là điểm P.
Đáp án cần chọn là: D
Câu 10:
Gọi M và N lần lượt là điểm biểu diễn của các số phức \[{z_1};{z_2}\;\] khác 0. Khi đó khẳng định nào sau đây sai ?
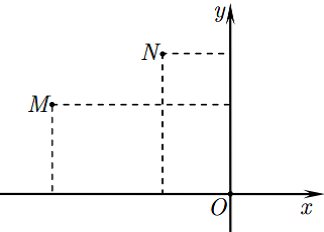
Ta có:\[\left| {{z_1} + {z_2}} \right| = MN\] là khẳng định sai vì dựa vào đồ thị ta có:\[\left| {{z_1} - {z_2}} \right| = MN\]
Đáp án cần chọn là: C
Câu 11:
Số phức z được biểu diễn trên trên mặt phẳng như hình vẽ.
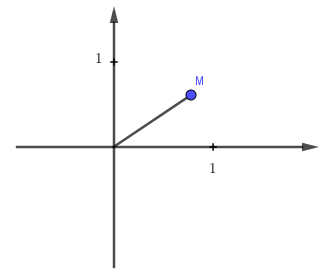
Hỏi hình nào biểu diễn cho số phức \[w = \frac{i}{{\overline z }}\]
Giả sử\[z = a + bi\] với\[0 < a,b < 1\]
Có\[w = \frac{i}{{\bar z}} = \frac{i}{{a - bi}} = \frac{{i(a + bi)}}{{{a^2} + {b^2}}} = \frac{{ - b}}{{{a^2} + {b^2}}} + \frac{{ai}}{{{a^2} + {b^2}}}\]
Vì z thuộc góc phần tư thứ I nên\[ - \frac{b}{{{a^2} + {b^2}}} < 0;\frac{a}{{{a^2} + {b^2}}} > 0\] Do đó w thuộc góc phần tư thứ II.</>
Đáp án cần chọn là: B
</>
Câu 12:
Trong mặt phẳng phức gọi A,B,C lần lượt là các điểm biểu diễn của các số phức \[{z_1} = 3 + 2i;{z_2} = 3 - 2i;{z_3} = - 3 - 2i\]. Khẳng định nào sau đây là sai?
Ta có:
\[{z_1} = 3 + 2i \Rightarrow A\left( {3;2} \right);{z_2} = 3 - 2i \Rightarrow B\left( {3; - 2} \right);{z_3} = - 3 - 2i \Rightarrow C\left( { - 3; - 2} \right)\]
Suy ta trọng tâm của\[{\rm{\Delta }}ABC\] là\[\left( {1; - \frac{2}{3}} \right)\] suy ra phương án B sai.
Đáp án cần chọn là: B
Câu 13:
Tập điểm biểu diễn số phức z thỏa mãn \[{\left| z \right|^2} = {z^2}\] là:
Đặt\[z = x + yi\left( {x,y \in R} \right)\]thì
\[|z{|^2} = {z^2} \Leftrightarrow {x^2} + {y^2} = {x^2} + 2xyi - {y^2}\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{xy = 0}\\{{x^2} + {y^2} = {x^2} - {y^2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \in R}\\{y = 0}\end{array}} \right.\)
Do đó tập điểm biểu diễn z là đường thẳng y=0
Đáp án cần chọn là: B
Câu 15:
Cho số phức z thỏa mãn \[{\left( {1 + z} \right)^2}\] là số thực. Tập hợp điểm MM biểu diễn số phức z là:
\[{\left( {1 + z} \right)^2} = {(1 + x + iy)^2} = {\left( {1 + x} \right)^2} - {y^2} + 2(1 + x)yi\]
Để\[{\left( {1 + z} \right)^2}\]là số thực thì\[2(1 + x)y = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1}\\{y = 0}\end{array}} \right.\]
Vậy tập hợp các điểm M thỏa mãn là hai đường thẳng\[x = - 1\]và\[y = 0\]
Đáp án cần chọn là: C
Câu 16:
Cho số phức z thay đổi, luôn có \[\left| z \right| = 2\;\]. Khi đó tập hợp điểm biểu diễn số phức \[w = \left( {1 - 2i} \right)\overline z + 3i\;\] là
Giả sử\[{\rm{w}} = a + bi(a,b \in R) \Rightarrow a + bi = (1 - 2i)\bar z + 3i\]
\[ \Rightarrow \overline z = \frac{{a + (b - 3)i}}{{1 - 2i}} = \frac{{[a + (b - 3)i](1 + 2i)}}{5} = \frac{{a - 2(b - 3) + (2a + b - 3)i}}{5}\]
\( \Rightarrow \left| {\overline z } \right| = \frac{1}{5}\sqrt {{{[a - 2(b - 3)]}^2} + {{(2a + b - 3)}^2}} = 2\)
\[ \Rightarrow {(a - 2b + 6)^2} + {(2a + b - 3)^2} = 100\]
\[ \Rightarrow {(a - 2b)^2} + {(2a + b)^2} + 12(a - 2b) - 6(2a + b) = 55\]
\[ \Rightarrow 5{a^2} + 5{b^2} - 30b = 55\]
\[ \Rightarrow {a^2} + {b^2} - 6b = 11\]
\[ \Rightarrow {a^2} + {(b - 3)^2} = 20\]
Đáp án cần chọn là: C
Câu 17:
Cho các số phức z thỏa mãn \[\left| z \right| = 4\;\]. Biết rằng tập hợp các điểm biểu diễn số phức\[w = \left( {3 + 4i} \right)z + i\;\]là một đường tròn. Tính bán kính r của đường tròn đó.
\[w = x + yi(x,y \in R)\]
\[\begin{array}{l} \Rightarrow z = \frac{{w - i}}{{3 + 4i}} = \frac{{x + (y - 1)i}}{{3 + 4i}} = \frac{{3x + 4(y - 1) + [3(y - 1) - 4x]i}}{{25}}\\16 = |z{|^2} = {\left( {\frac{{3x + 4y - 4}}{{25}}} \right)^2} + {\left( {\frac{{ - 4x + 3y - 3}}{{25}}} \right)^2}\\{\left[ {\frac{3}{{25}}x + \frac{4}{{25}}\left( {y - 1} \right)} \right]^2} + {\left[ {\frac{{ - 4}}{{25}}x + \frac{3}{{25}}\left( {y - 1} \right)} \right]^2} = 16\\ \Leftrightarrow {x^2}\left[ {{{\left( {\frac{3}{{25}}} \right)}^2} + {{\left( { - \frac{4}{{25}}} \right)}^2}} \right] + {(y - 1)^2}\left[ {{{\left( {\frac{4}{{25}}} \right)}^2} + {{\left( {\frac{3}{{25}}} \right)}^2}} \right] = 16\\ \Leftrightarrow {x^2}.\frac{1}{{25}} + {(y - 1)^2}.\frac{1}{{25}} = 16\\ \Rightarrow {x^2} + {(y - 1)^2} = 400 \Rightarrow r = 20\end{array}\]
Đáp án cần chọn là: C
Câu 18:
Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thoả mãn điều kiện \[2\left| {z - i} \right| = \left| {z - \overline z + 2i} \right|\] là hình gì?
Đặt
\[\begin{array}{*{20}{l}}{z = a + bi;a,b \in R;{i^2} = - 1}\\{ \Rightarrow z - i = a + \left( {b - 1} \right)i}\\{ \Rightarrow z - \bar z + 2i = \left( {2 + 2b} \right)i}\\{ \Rightarrow \left| {z - \bar z + 2i} \right| = 2\left| {z - i} \right| \Leftrightarrow \sqrt {{{\left( {2 + 2b} \right)}^2}} = 2\sqrt {{a^2} + {{\left( {b - 1} \right)}^2}} }\\{ \Leftrightarrow 4{a^2} - 16b = 0 \Leftrightarrow b = \frac{1}{4}{a^2}}\end{array}\]
Tập hợp các điểm biểu diễn số phức là đường parabol
Đáp án cần chọn là: B
Câu 19:
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức zz thỏa mãn điều kiện \[\left| {z - 2} \right| + \left| {z + 2} \right| = 10.\]
Gọi \[z = x + yi\]. Khi đó điểm M(x;y) biểu diễn số phức z.
Ta có :\[\left| {z - 2} \right| + \left| {z + 2} \right| = 10 \Leftrightarrow \left| {x - 2 + yi} \right| + \left| {x + 2 + yi} \right| = 10\]
\[ \Leftrightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {y^2}} + \sqrt {{{\left( {x + 2} \right)}^2} + {y^2}} = 10\]
Đặt F1(−2;0);F2(2;0), khi đó :\[M{F_1} + M{F_2} = 10 > {F_1}{F_2}( = 4)\] nên tập hợp các điểm MM là elip (E) có 2 tiêu điểm là \[{F_1};{F_2}\]. Gọi (E) có dạng :\[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\]
Ta có
\(\left\{ {\begin{array}{*{20}{c}}{M{F_1} + M{F_2} = 10 = 2a}\\{{F_1}{F_2} = 4 = 2c}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 5}\\{c = 2}\end{array}} \right. \Rightarrow b = \sqrt {{5^2} - {2^2}} = \sqrt {21} \)
Vậy tập hợp các điểm M là elip : \[(E):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{21}} = 1\]
Đáp án cần chọn là: D
Câu 20:
Cho số phức \[z = \left( {m + 3} \right) + \left( {{m^2} - m - 6} \right)i\] với \[m \in \mathbb{R}\] Gọi (P) là tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng
Ta có\[z = \left( {m + 3} \right) + \left( {{m^2} - m - 6} \right)i\] được biểu diễn bởi điểm M(x;y) với
\(\left\{ {\begin{array}{*{20}{c}}{x = m + 3}\\{y = {m^2} - m - 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m = x - 3}\\{y = {{(x - 3)}^2} - (x - 3) - 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m = x - 3}\\{y = {x^2} - 7x + 6}\end{array}} \right.\)
Vậy tập hợp điểm biểu diễn số phức z là parabol\[\left( P \right):y = {x^2} - 7x + 6\]
Hoành độ giao điểm của parabol (P) với trục hoành là\[{x^2} - 7x + 6 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 6}\end{array}} \right.\]
Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng
\[S = \mathop \smallint \limits_1^6 \left| {{x^2} - 7x + 6} \right|dx = \left| {\mathop \smallint \limits_1^6 \left( {{x^2} - 7x + 6} \right)dx} \right| = \frac{{125}}{6}\]
Đáp án cần chọn là: A
Câu 21:
Cho hai số phức \[{z_1},{z_2}\;\] thỏa mãn \[\left| {{z_1}} \right| = 6,\left| {{z_2}} \right| = 2\]. Gọi M,N lần lượt là các điểm biểu diễn của số phức \[{z_1}\] và số phức \[i{z_2}_{}\]. Biết \(\widehat {MON} = {60^ \circ }\). Tính \[T = \left| {z_1^2 + 9z_2^2} \right|\]
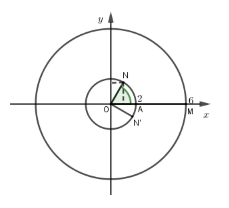
Ta chọn \[{z_1} = 6\;\] có điểm biểu diễn là M(6;0).
Khi đó\[\widehat {MON} = {60^0}\] nên chọn\[N\left( {1;\sqrt 3 } \right)\] (hình vẽ) biểu diễn số phức\[i{z_2}\]
Suy ra điểm\[N'\left( {\sqrt 3 ; - 1} \right)\] biểu diễn số phức\[{z_2}\] hay\[{z_2} = \sqrt 3 - i\]
Khi đó\[T = \left| {z_1^2 + 9z_2^2} \right| = \left| {{6^2} + 9{{\left( {\sqrt 3 - i} \right)}^2}} \right| = 36\sqrt 3 \]
Đáp án cần chọn là: B
Câu 22:
Trên mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn hình học của số phức \[z = - 1 + 2i\;\] và \[\alpha \] là góc lượng giác có tia đầu Ox, tia cuối OM. Tính \[tan2\alpha .\]
Ta có:\[z = - 1 + 2i\] có điểm biểu diễn là\[M\left( { - 1;\,\,2} \right).\]
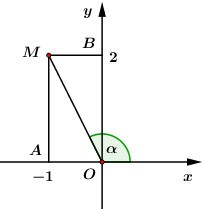
Ta có:\[\tan AOM = \frac{{AM}}{{OA}} = \frac{2}{1} = 2.\]
\[ \Rightarrow \tan \alpha = - \tan AOM = - 2\] (hai góc bù nhau)
\[ \Rightarrow \tan 2\alpha = \frac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }} = \frac{{2.\left( { - 2} \right)}}{{1 - {{\left( { - 2} \right)}^2}}} = \frac{4}{3}\]
Đáp án cần chọn là: D
Câu 23:
Biết rằng điểm biểu diễn số phức z là điểm M ở hình bên dưới. Modun của z bằng:
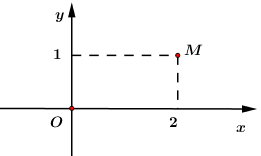
Từ hình vẽ ta thấy\[M\left( {2;\,\,1} \right)\] là điểm biểu diễn số phức \[z \Rightarrow z = 2 + i\]
⇒ Modun của số phức z là:\(\)\[\left| z \right| = \sqrt {{2^2} + 1} = \sqrt 5 .\]
Đáp án cần chọn là: B
Câu 24:
Gọi A và B lần lượt là điểm biểu diễn của số phức \[{z_1} = 3 - 2i\;\] và \[{z_2} = 1 + 4i.\] Trung điểm của đoạn thẳng AB có tọa độ là:
Vì A và B lần lượt là điểm biểu diễn của số phức \[{z_1} = 3 - 2i\] và\[{z_2} = 1 + 4i\] nên\[A\left( {3; - 2} \right)\] và\[B\left( {1;4} \right)\]
Gọi M là trung điểm của AB \[ \Rightarrow M\left( {\frac{{3 + 1}}{2};\frac{{ - 2 + 4}}{2}} \right) \Rightarrow M\left( {2;1} \right)\]Đáp án cần chọn là: C
Câu 25:
Cho các số phức \[{z_1} = 3 - 2i,{z_2} = 1 + 4i\] và \[{z_3} = - 1 + i\;\] có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A,B,C. Diện tích tam giác ABC bằng:
Ta có\[{z_1} = 3 - 2i,{z_2} = 1 + 4i\] và\[{z_3} = - 1 + i\] có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A,B,C nên\[A\left( {3; - 2} \right);\,\,B\left( {1;4} \right);\,\,C\left( { - 1;1} \right).\]
Khi đó ta có:
\[\begin{array}{*{20}{l}}{AB = \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( {4 + 2} \right)}^2}} = 2\sqrt {10} }\\{AC = \sqrt {{{\left( { - 1 - 3} \right)}^2} + {{\left( {1 + 2} \right)}^2}} = 5}\\{BC = \sqrt {{{\left( { - 1 - 1} \right)}^2} + {{\left( {1 - 4} \right)}^2}} = \sqrt {13} }\end{array}\]
Gọi p là nửa chu vi tam giác ABC ta có:\[p = \frac{{2\sqrt {10} + 5 + \sqrt {13} }}{2}.\]
Diện tích tam giác ABC là:\[{S_{{\rm{\Delta }}ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} = 9.\]
Đáp án cần chọn là: D
Câu 26:
Cho hai số phức \[{z_1} = 3 + i,{z_2} = - 1 + 2i\]. Trong mặt phẳng tọa độ, điểm biểu diễn cho số phức \[w = 2{z_1} - {z_2}\;\] là:
Ta có
\[\begin{array}{*{20}{l}}{w = 2{z_1} - {z_2}}\\{\,\,\,\,\, = 2\left( {3 + i} \right) - \left( { - 1 + 2i} \right)}\\{\,\,\,\,\, = 6 + 2i + 1 - 2i = 7}\end{array}\]
Vậy điểm biểu diễn của số phức w là M(7;0).
Đáp án cần chọn là: C
Câu 27:
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \[z.\overline z = 1\;\] là:
Bước 1:
Gọi\[z = x + yi\left( {x;y \in R} \right)\] khi đó\[\bar z = x - yi\]
Bước 2:
Ta có:\[z.\bar z = 1 \Leftrightarrow \left( {x + yi} \right)\left( {x - yi} \right) = 1 \Leftrightarrow {x^2} - {\left( {yi} \right)^2} = 1 \Leftrightarrow {x^2} + {y^2} = 1\]
Vậy tập hợp điểm biểu diễn số phức z là một đường tròn.
Đáp án cần chọn là: B
Câu 28:
Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \[{z_1} = - 1 + i,\;{z_2} = 1 + 2i,{z_3} = 2 - i,{z_4} = - 3i\]. Gọi S diện tích tứ giác ABCD. Tính S.
Ta có: \[A\left( { - 1;1} \right);\,\,B\left( {1;2} \right);\,\,C\left( {2; - 1} \right);\,\,D\left( {0; - 3} \right)\]
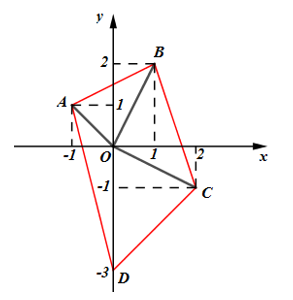
Phương trình AB:
\[\frac{{x + 1}}{{1 + 1}} = \frac{{y - 1}}{{2 - 1}} \Leftrightarrow x + 1 = 2y - 2 \Leftrightarrow x - 2y + 3 = 0 \Rightarrow d\left( {O;AB} \right) = \frac{3}{{\sqrt 5 }};\,\,AB = \sqrt 5 \]
\[ \Rightarrow {S_{{\rm{\Delta }}OAB}} = \frac{1}{2}d\left( {O;AB} \right).AB = \frac{1}{2}.\frac{3}{{\sqrt 5 }}.\sqrt 5 = \frac{3}{2}\]
Phương trình BC:
\[\frac{{x - 1}}{{2 - 1}} = \frac{{y - 2}}{{ - 1 - 2}} \Leftrightarrow - 3x + 3 = y - 2 \Leftrightarrow 3x + y - 5 = 0 \Rightarrow d\left( {O;BC} \right) = \frac{5}{{\sqrt {10} }};\,\,BC = \sqrt {10} \]
\[ \Rightarrow {S_{{\rm{\Delta }}OBC}} = \frac{1}{2}d\left( {O;BC} \right).BC = \frac{1}{2}.\frac{5}{{\sqrt {10} .\sqrt {10} }} = \frac{5}{2}\]
Phương trình CD:
\[\frac{{x - 2}}{{0 - 2}} = \frac{{y + 1}}{{ - 3 + 1}} \Leftrightarrow - 2x + 4 = - 2y - 2 \Leftrightarrow x - y - 3 = 0 \Rightarrow d\left( {O;CD} \right) = \frac{3}{{\sqrt 2 }};\,\,CD = 2\sqrt 2 \]
\[ \Rightarrow {S_{{\rm{\Delta }}OCD}} = \frac{1}{2}.\frac{3}{{\sqrt 2 }}.2\sqrt 2 = 3\]
Phương trình AD:\[\frac{{x + 1}}{{0 + 1}} = \frac{{y - 1}}{{ - 3 - 1}} \Leftrightarrow - 4x - 4 = y - 1 \Leftrightarrow 4x + y + 3 = 0 \Rightarrow d\left( {O;AD} \right) = \frac{3}{{\sqrt {17} }};\,\,AD = \sqrt {17} \]
\[ \Rightarrow {S_{{\rm{\Delta }}OAD}} = \frac{1}{2}.\frac{3}{{\sqrt {17} }}.\sqrt {17} = \frac{3}{2}\]
Vậy\[S = {S_{{\rm{\Delta }}OAB}} + {S_{{\rm{\Delta }}OBC}} + {S_{{\rm{\Delta }}OCD}} + {S_{{\rm{\Delta }}OAD}} = \frac{{17}}{2}\]
Đáp án cần chọn là: A
Câu 29:
Cho các số phức \[{z_1} = 2,{z_2} = - 4i,{z_3} = 2 - 4i\] có điểm biểu diễn tương ứng trên mặt phẳng tọa độ Oxy là A, B, C. Diện tích tam giác ABC bằng
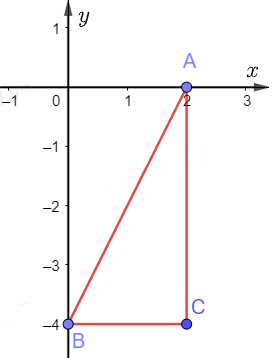
Các điểm biểu diễn trên mặt phẳng tọa độ: A(2;0), B(0;-4), C(2;-4).
Ta thấy tam giác ABC vuông tại C với độ dài hai cạnh góc vuông là: 2 và 4.
\[{S_{ABC}} = \frac{1}{2}.AC.BC = \frac{1}{2}.4.2 = 4\]
Đáp án cần chọn là: C
Câu 30:
Cho các số phức z thỏa mãn \[\left| z \right| = {\rm{ }}2\]và điểm A trong hình vẽ là điểm biểu diễn của z. Biết rằng trong hình vẽ, điểm biểu diễn số phức \[w = \frac{{ - 4}}{z}\] là một trong bốn điểm M, N, P, Q
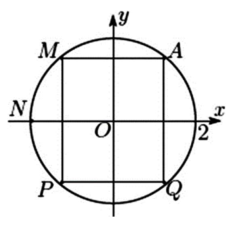
Khi đó điểm biểu diễn của số phức w là
Đặt \[z = x + yi = > {x^2} + {y^2} = 4 = > A\left( {x;y} \right)\]
Xét\[w = \frac{{ - 4}}{z} = \frac{{ - \left( {{x^2} + {y^2}} \right)}}{{x + yi}} = \frac{{ - \left( {x + yi} \right)\left( {x - yi} \right)}}{{\left( {x + yi} \right)}} = - x + yi\]
Điểm biểu diễn số phức w đối xứng A qua Oy
=> Điểm M.
Đáp án cần chọn là: D
Câu 31:
Biết rằng tập hợp điểm biểu diễn các số phức z thỏa mãn \[\left| {\left( {1 + i} \right)z + 5 - i} \right| = 1\;\]là đường tròn tâm I(a;b). Tính a+b.
Bước 1: Chia cả 2 vế của phương trình ban đầu cho \[\left| {1 + i} \right|\]
Thay vào giả thiết ta có:
\[\left| {\left( {1 + i} \right)z + 5 - i} \right| = 1\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow \frac{{\left| {\left( {1 + i} \right)z + 5 - i} \right|}}{{\left| {1 + i} \right|}} = \frac{1}{{\left| {1 + i} \right|}}}\\{ \Leftrightarrow \left| {\frac{{\left( {1 + i} \right)z + 5 - i}}{{1 + i}}} \right| = \frac{1}{{\left| {1 + i} \right|}}}\end{array}\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow \left| {z + \frac{{5 - i}}{{1 + i}}} \right| = \frac{1}{{\left| {1 + i} \right|}}}\\{ \Leftrightarrow \left| {z + 2 - 3i} \right| = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}}\\{ \Leftrightarrow \left| {z - \left( { - 2 + 3i} \right)} \right| = \frac{{\sqrt 2 }}{2}}\end{array}\]
Bước 2: Tìm tâm và bán kính của đường tròn
Suy ra tập hợp các điểm biểu diễn số phức zz là đường tròn tâm
\[I( - 2;3) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 2}\\{b = 3}\end{array}} \right.\]
Vậy\[a + b = - 2 + 3 = 1\]
Câu 32:
Cho số phức z thỏa mãn \[\left| {z + i} \right| = 1\]. Biết rằng tập hợp các điểm biểu diễn số phức \[w = \left( {3 + 4i} \right)z + 2 + i\] là một đường tròn tâm I, điểm I có tọa độ là I(a;b), tính a−b
Bước 1: Biểu diễn z theo w.
\[w = \left( {3 + 4i} \right)z + 2 + i \Leftrightarrow \left( {3 + 4i} \right)z = w - 2 - i \Leftrightarrow z = \frac{{w - 2 - i}}{{3 + 4i}}\]
Bước 2: Biến đổi phương trình ban đầu thành dạng \[\left| {w\left( {a + bi} \right)} \right| = R\]
Theo bài ra ta có:
\[\begin{array}{*{20}{l}}{\left| {z + i} \right| = 1 \Leftrightarrow \left| {\frac{{w - 2 - i}}{{3 + 4i}} + i} \right| = 1 \Leftrightarrow \left| {\frac{{w - 2 - i + 3i - 4}}{{3 + 4i}}} \right| = 1}\\{ \Leftrightarrow \frac{{\left| {w - 6 + 2i} \right|}}{{\left| {3 + 4i} \right|}} = 1 \Leftrightarrow \left| {w - \left( {6 - 2i} \right)} \right| = 5}\end{array}\]
=> Tập hợp các điểm biểu diễn số phức w là đường tròn tâm I(6;−2) bán kính R=5.
Vậy a−b=8
Câu 33:
Trong mặt phẳng tọa độ, tập hợp các điểm M biểu diễn của số phức z thỏa mãn\[\left| {z + 1 + 3i} \right| = \left| {z - 2 - i} \right|\;\]là phương trình đường thẳng có dạng \[ax + by + c = 0\]. Khi đó tỉ số abab bằng:
Bước 1:
Đặt \[z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right).\]
Bước 2: Biến đổi rút ra mối quan hệ giữa a,ba,b và suy ra quỹ tích các điểm biểu diễn số phức zz.
Theo bài ra ta có:
\[\begin{array}{*{20}{l}}{\,\,\,\,\,\,\,\left| {z + 1 + 3i} \right| = \left| {z - 2 - i} \right|}\\{ \Leftrightarrow \left| {a + bi + 1 + 3i} \right| = \left| {a + bi - 2 - i} \right|}\\{ \Leftrightarrow {{\left( {a + 1} \right)}^2} + {{\left( {b + 3} \right)}^2} = {{\left( {a - 2} \right)}^2} + {{\left( {b - 1} \right)}^2}}\\{ \Leftrightarrow {a^2} + 2a + 1 + {b^2} + 6b + 9 = {a^2} - 4a + 4 + {b^2} - 2b + 1}\\{ \Leftrightarrow 6a + 8b + 5 = 0}\end{array}\]
Suy ra tập hợp các điểm M biểu diễn số phức z là đường thẳng\[6x + 8y + 5 = 0\]
Vậy\[\frac{a}{b} = \frac{6}{8} = \frac{3}{4}\]
Câu 34:
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \[z.\overline z = 1\;\] là đường tròn có bán kính là:
Gọi\[z = x + yi\left( {x;y \in R} \right)\] khi đó\[\bar z = x - yi\]
Ta có:\[z.\bar z = 1 \Leftrightarrow \left( {x + yi} \right)\left( {x - yi} \right) = 1 \Leftrightarrow {x^2} - {\left( {yi} \right)^2} = 1 \Leftrightarrow {x^2} + {y^2} = 1\]
Vậy tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 1.
