Hàm số logarit
-
342 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hàm số \[y = {\log _a}x(0 < a \ne 1)\] xác định trên:
Hàm số \[y = {\log _a}x(0 < a \ne 1)\] xác định trên \[\left( {0; + \infty } \right)\]
Đáp án cần chọn là: D
Câu 2:
Hàm số \[y = {\log _a}x\] có đạo hàm là:
Điều kiện xác định: x>0
Đạo hàm hàm số\[y = {\log _a}x\] là \[y' = \frac{1}{{x\ln a}}\]
Đáp án cần chọn là: C
Câu 3:
Chọn mệnh đề đúng:
Giới hạn cần nhớ: \[\mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{x} = 1\]
Đáp án cần chọn là: A
Câu 4:
Tiệm cận đứng của đồ thị hàm số \[y = {\log _a}x(0 < a \ne 1)\] là đường thẳng:
Đồ thị hàm số \[y = {\log _a}x(0 < a \ne 1)\] có đường tiệm cận đứng là x=0 (trục Oy)
Đáp án cần chọn là: D
Câu 5:
Điểm \[({x_0};{y_0})\;\]thuộc đồ thị hàm số \[y = lo{g_a}x(0 < a \ne 1)\;\] nếu:
Điểm\[\left( {{x_0};{y_0}} \right)\] thuộc đồ thị hàm số \[y = lo{g_a}x(0 < a \ne 1)\;\] nếu\[{y_0} = {\log _a}{x_0}\]
Đáp án cần chọn là: A
Câu 6:
Điểm nào sau đây không thuộc đồ thị hàm số \[y = lo{g_a}x(0 < a \ne 1)\;\]?
Đồ thị hàm số luôn đi qua các điểm (1;0) và (a;1).
- Với \[x = {a^2}\] thì \[y = {\log _a}x = {\log _a}{a^2} = 2\] nên đồ thị hàm số đi qua \[\left( {{a^2};2} \right)\]nên C sai, D đúng.
Đáp án cần chọn là: C
Câu 7:
Cho hàm số \[y = {\log _{\frac{\pi }{4}}}x\]. Khẳng định nào sau đây sai?
- Hàm số \[y = {\log _{\frac{\pi }{4}}}x\] có tập xác định \[D = \left( {0; + \infty } \right)\]
- Vì \(0 < \frac{\pi }{4} < 1\)nên hàm số nghịch biến trên TXĐ
- Tiệm cận đứng của đồ thị hàm số là trục Oy
- Đồ thị hàm số nằm hoàn toàn bên phải trục hoành (vì x>0)
Đáp án cần chọn là: D
Câu 8:
Gọi (C) là đồ thị hàm số y=logx. Tìm khẳng định đúng?
- Đồ thị hàm số y=logx nhận trục tung là tiệm cận đứng.
- Đồ thị hàm số không có tiệm cận ngang và cắt trục hoành tại điểm (1;0) nên các đáp án B,C,D đều sai
Đáp án cần chọn là: A
Câu 9:
Trong các khẳng định sau, khẳng định nào đúng?
\[\log a + \log b = \log \left( {ab} \right)\]nên ý A sai
Nhận thấy \[{a^{x + y}} = {a^x}.{a^y}\] nên mệnh đề ở ý B sai.
Vì 12>1 nên \[y = {\log _{12}}x\] là hàm đồng biến trên khoảng \[(0; + \infty )\]nên D sai
Đáp án cần chọn là: C
Câu 10:
Cho a,b là các số thực, thỏa mãn 0<a<1<b, khẳng định nào sau đây là đúng?
Ta có: 0<a<1 nên hàm số \[y = {\log _a}x\] nghịch biến, do đó b>1 nên \[{\log _a}b < {\log _a}1 = 0\].
Vì b>1 nên hàm số \[y = {\log _b}x\] đồng biến, do đó a<1 nên \[lo{g_b}a < {\log _b}1 = 0\]
Vậy \[{\log _a}b < 0;{\log _b}a < 0 \Rightarrow {\log _a}b + {\log _b}a < 0\]
Đáp án cần chọn là: A
Câu 11:
Cho \[a > 0,a \ne 1\]. Tìm mệnh đề đúng trong các mệnh đề sau:
Cho \[a > 0;a \ne 1\] khi đó hàm số \[y = {a^x}\] có tập xác định là R , tập giá trị là \[\left( {0; + \infty } \right)\]
Hàm số \[y = {\log _a}x\] có tập xác định là \[\left( {0; + \infty } \right)\], tập giá trị là R
Suy ra B đúng
Đáp án cần chọn là: B
Câu 12:
Tìm tập xác định D của hàm số \[y = {\log _{\sqrt 2 }}\left( {\frac{{ - 3}}{{2 - 2x}}} \right)\]
Đáp án cần chọn là: D
Câu 13:
Đạo hàm hàm số \[y = {\log _{2018}}\left( {2018x + 1} \right)\] là:
Ta có:
\[{\left[ {{{\log }_{2018}}\left( {2018x + 1} \right)} \right]^\prime } = \frac{{{{\left( {2018x + 1} \right)}^\prime }}}{{\left( {2018x + 1} \right)\ln 2018}} = \frac{{2018}}{{\left( {2018x + 1} \right)\ln 2018}}\]
Đáp án cần chọn là: D
Câu 14:
Tính đạo hàm hàm số \[y = \ln \left( {1 + \sqrt {x + 1} } \right)\]
Ta có:
\[y' = {\left[ {\ln \left( {1 + \sqrt {x + 1} } \right)} \right]^\prime } = \frac{{{{\left( {1 + \sqrt {x + 1} } \right)}^\prime }}}{{1 + \sqrt {x + 1} }} = \frac{{\frac{1}{{2\sqrt {x + 1} }}}}{{1 + \sqrt {x + 1} }} = \frac{1}{{2\sqrt {x + 1} \left( {1 + \sqrt {x + 1} } \right)}}\]
Đáp án cần chọn là: A
Câu 15:
Cho a,b là các số thực dương, thỏa mãn \[{a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}\] và \[{\log _b}\frac{1}{2} < {\log _b}\frac{2}{3}\]. Mệnh đề nào dưới đây đúng?
Ta có:
\[\frac{3}{4} < \frac{4}{5}\] và \[{a^{\frac{3}{4}}} > {a^{\frac{4}{5}}} \Rightarrow 0 < a < 1\]
\[\frac{1}{2} < \frac{2}{3}\]và \[{\log _b}\frac{1}{2} < {\log _b}\frac{2}{3} \Rightarrow b > 1\]
Đáp án cần chọn là: C
Câu 16:
Hàm số nào trong các hàm số sau có đồ thị phù hợp với hình vẽ bên?
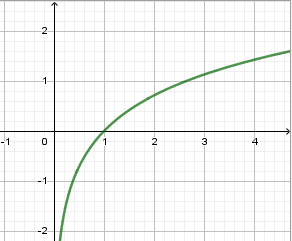
Đồ thị hàm số đã cho có \[y \to - \infty \]khi \[x \to {0^ + }\] nên nó là đồ thị hàm số \[y = lo{g_a}x\] với a>1
Đáp án cần chọn là: D
Câu 17:
Nếu gọi \[({G_1})\]là đồ thị hàm số \[y = {a^x}\;\] và \[({G_2})\]là đồ thị hàm số \[y = lo{g_a}x\;\] với \[0 < a \ne 1\]. Mệnh đề nào dưới đây đúng ?
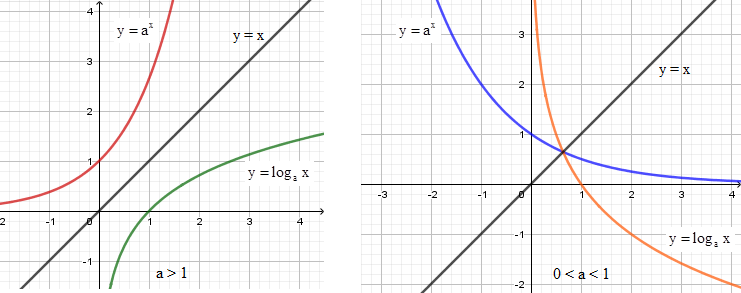
Quan sát hình vẽ ta thấy hai đồ thị hàm số đối xứng nhau qua đường thẳng y=x.
Đáp án cần chọn là: C
Câu 18:
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số \[y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\] được cho trong hình vẽ sau:
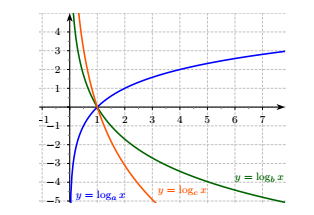
Mệnh đề nào dưới đây đúng?
Quan sát hình vẽ ta thấy:
- Hàm số \[y = {\log _a}x\] là hàm đồng biến nên ta có a>1 .
- Hai hàm số \[y = {\log _b}x,y = {\log _c}x\] nghịch biến nên có 0 Từ nhận xét này ta thấy a là số lớn nhất. Đáp án cần chọn là: B
Câu 19:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = log\left( {{x^2} - 2mx + 4} \right)\]có tập xác định là R
Giải điều kiện: \[{x^2} - 2mx + 4 > 0,\forall x \in R\]
\[{\rm{\Delta '}} = {m^2} - 4 < 0 \Leftrightarrow (m - 2)(m + 2) < 0\]Suy ra \[ - 2 < m < 2\]
Đáp án cần chọn là: D
Câu 20:
Cho x,y là các số thực thỏa mãn \[{\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1\]. Tìm giá trị nhỏ nhất Pmin của biểu thức \[P = 2x - y.\]
Điều kiện : \[x + y > 0,x--y > 0\]
\[{\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1 \Leftrightarrow {\log _4}\left( {{x^2} - {y^2}} \right) \ge 1 \Leftrightarrow {x^2} - {y^2} \ge 4\]
Ta có:
\[P = 2x - y = \frac{{x + y + 3(x - y)}}{2} \ge \sqrt {(x + y).3(x - y)} = \sqrt {3({x^2} - {y^2})} = \sqrt {3.4} = 2\sqrt 3 \]
Dấu “=” xảy ra khi:
\(\left\{ {\begin{array}{*{20}{c}}{x + y = 3(x - y)}\\{{x^2} - {y^2} = 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + y = 3(x - y)}\\{3{{(x - y)}^2} = 4}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x - y = \frac{2}{{\sqrt 3 }}}\\{x + y = 2\sqrt 3 }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{1}{{\sqrt 3 }} + \sqrt 3 }\\{y = \sqrt 3 - \frac{1}{{\sqrt 3 }}}\end{array}} \right.\)
Vậy \[Min\,P = 2\sqrt 3 \]
Đáp án cần chọn là: C
Câu 21:
Tìm tập giá trị T của hàm số \[f'\left( x \right) = \frac{{1 - \ln x}}{{{x^2}}}\] với \[x \in [1;{e^2}].\]
Hàm số f(x) xác định và liên tục trên đoạn\[\left[ {1;{e^2}} \right]\]
Đạo hàm\[f'\left( x \right) = \frac{{1 - \ln x}}{{{x^2}}} \Rightarrow f'\left( x \right) = 0 \Leftrightarrow 1 - \ln x = 0 \Leftrightarrow x = e \in \left[ {1;{e^2}} \right]\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{f(1) = 0}\\{f(e) = \frac{1}{e}}\\{f({e^2}) = \frac{2}{{{e^2}}}}\end{array}} \right.\)\[ \Rightarrow \mathop {\min }\limits_{x \in \left[ {1;{e^2}} \right]} f\left( x \right) = 0,\mathop {\max }\limits_{x \in \left[ {1;{e^2}} \right]} f\left( x \right) = \frac{1}{e} \Rightarrow {\rm{T}} = \left[ {0;\frac{1}{e}} \right]\]
Đáp án cần chọn là: C
Câu 22:
Tìm tham số m để hàm số \[y = \frac{{{{\log }_{\frac{1}{2}}}x - 2}}{{{{\log }_2}x - m}}\] đồng biến trên khoảng (0;1).
Ta có: \[y = \frac{{{{\log }_{\frac{1}{2}}}x - 2}}{{{{\log }_2}x - m}} = \frac{{ - {{\log }_2}x - 2}}{{{{\log }_2}x - m}}\]
Đặt \[t = {\log _2}x\] với\[x \in \left( {0;1} \right) \Rightarrow t \in \left( { - \infty ;0} \right)\]
⇒ Hàm số\[y = \frac{{{{\log }_{\frac{1}{2}}}x - 2}}{{{{\log }_2}x - m}}\] đồng biến trên khoảng (0;1) khi và chỉ khi\[y = f\left( t \right) = \frac{{ - t - 2}}{{t - m}}\] đồng biến trên\[\left( { - \infty ;0} \right)\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y\prime = \frac{{m + 2}}{{{{(t - m)}^2}}} > 0}\\{m \notin ( - \infty ;0)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m > - 2}\\{m \ge 0}\end{array}} \right. \Leftrightarrow m \ge 0\)
Đáp án cần chọn là: C
Câu 23:
Hàm số \[y = {\log _a}x\]và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng y = 3 cắt hai đồ thị tại các điểm có hoành độ \[{x_1},{x_2}\]. Biết rằng \[{x_2} = 2{x_1},\], giá trị của ab bằng:
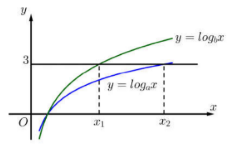
Dựa vào đồ thị hàm số ta thấy \[{x_1}\] là nghiệm của phương trình hoành độ giao điểm \[{\log _b}{x_1} = 3 \Leftrightarrow {x_1} = {b^3}.\].
Và \[{x_2}\] là nghiệm của phương trình hoành độ giao điểm \[{\log _a}{x_2} = 3 \Leftrightarrow {x_2} = {a^3}.\]
Theo đề bài ta có: \[{x_2} = 2{x_1} \Rightarrow {a^3} = 2{b^3} \Leftrightarrow \frac{{{a^3}}}{{{b^3}}} = 2 \Leftrightarrow \frac{a}{b} = \sqrt[3]{2}.\]
Đáp án cần chọn là: D
Câu 24:
Hàm số \[y = {\log _{\frac{e}{3}}}\left( {x - 1} \right)\] nghịch biến trên khoảng nào dưới đây?
Xét hàm số\[y = {\log _{\frac{e}{3}}}\left( {x - 1} \right)\] có TXĐ: \[D = \left( {1; + \infty } \right)\] và \[a = \frac{e}{3} < 1\]
⇒ Hàm số nghịch biến trên\[\left( {1; + \infty } \right).\]Đáp án cần chọn là: A
Câu 25:
Tập xác định của hàm số \[f\left( x \right) = {\log _{\frac{1}{2}}}\left( {{{\log }_4}\left( {{{\log }_{\frac{1}{4}}}\left( {{{\log }_{16}}\left( {{{\log }_{\frac{1}{{16}}}}x} \right)} \right)} \right)} \right)\] là một khoảng có độ dài n/m, với m và n là các số nguyên dương và nguyên tố cùng nhau. Khi đó m−n bằng:
Hàm số\[f\left( x \right) = {\log _{\frac{1}{2}}}\left( {{{\log }_4}\left( {{{\log }_{\frac{1}{4}}}\left( {{{\log }_{16}}\left( {{{\log }_{\frac{1}{{16}}}}x} \right)} \right)} \right)} \right)\] xác định
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > 0}\\{lo{g_{\frac{1}{{16}}}}x > 0}\\{lo{g_{16}}\left( {lo{g_{\frac{1}{{16}}}}x} \right) > 0}\\{lo{g_{\frac{1}{4}}}\left( {lo{g_{16}}\left( {lo{g_{\frac{1}{{16}}}}x} \right)} \right) > 0}\\{lo{g_4}\left( {lo{g_{\frac{1}{4}}}\left( {lo{g_{16}}\left( {lo{g_{\frac{1}{{16}}}}x} \right)} \right)} \right) > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > 0}\\{x < 1}\\{lo{g_{\frac{1}{{16}}}}x > 1}\\{\begin{array}{*{20}{c}}{lo{g_{16}}\left( {lo{g_{\frac{1}{{16}}}}x} \right) < 1}\\{lo{g_{\frac{1}{4}}}\left( {lo{g_{16}}\left( {lo{g_{\frac{1}{{16}}}}x} \right)} \right) > 1}\end{array}}\end{array}} \right.} \right.\)</></>
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 < x < 1}\\{x < \frac{1}{{16}}}\\{lo{g_{\frac{1}{{16}}}}x < 16}\\{lo{g_{16}}\left( {lo{g_{\frac{1}{{16}}}}x} \right) < \frac{1}{4}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 < x < 1}\\{x < \frac{1}{{16}}}\\{x > {{\left( {\frac{1}{{16}}} \right)}^{16}}}\\{lo{g_{\frac{1}{{16}}}}x < {{16}^{\frac{1}{4}}} = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\left( {\frac{1}{{16}}} \right)}^{16}} < x < \frac{1}{{16}}}\\{x > {{\left( {\frac{1}{{16}}} \right)}^2} = \frac{1}{{256}}}\end{array}} \right.\)
\( \Leftrightarrow \frac{1}{{256}} < x < \frac{1}{{16}}\)
Suy ra tập xác định của hàm số đã cho là\[D = \left( {\frac{1}{{256}};\frac{1}{{16}}} \right)\]
⇒ Tập xác định là khoảng có độ dài là\[\frac{1}{{16}} - \frac{1}{{256}} = \frac{{15}}{{256}} \Rightarrow n = 15,\,\,m = 256\]
Vậy\[m - n = 256 - 15 = 241\]
Đáp án cần chọn là: C
Câu 26:
Cho hai hàm số \[y = \ln \left| {\frac{{x - 2}}{x}} \right|\]và\(y = \frac{3}{{x - 2}} - \frac{1}{x} + 4m - 2020\). Tổng tất cả các giá trị nguyên của tham số m để hai đồ thị hàm số cắt nhau tại một điểm duy nhất bằng:
ĐKXĐ: \[x \ne 0,\,\,x \ne 2\]
Xét phương trình hoành độ giao điểm:
\[\begin{array}{*{20}{l}}{\ln \left| {\frac{{x - 2}}{x}} \right| = \frac{3}{{x - 2}} - \frac{1}{x} + 4m - 2020}\\{ \Leftrightarrow \ln \left| {\frac{{x - 2}}{x}} \right| - \frac{3}{{x - 2}} + \frac{1}{x} = 4m - 2020}\end{array}\]
Đặt \[f\left( x \right) = \ln \left| {\frac{{x - 2}}{x}} \right| - \frac{3}{{x - 2}} + \frac{1}{x}\]ta có:
\[\begin{array}{l}f\prime (x) = \frac{2}{{{x^2}}}:\frac{{x - 2}}{x} + \frac{3}{{{{(x - 2)}^2}}} - \frac{1}{{{x^2}}}\\f\prime (x) = \frac{2}{{x(x - 2)}} + \frac{3}{{{{(x - 2)}^2}}} - \frac{1}{{{x^2}}}\\f\prime (x) = \frac{{2x(x - 2) + 3{x^2} - {{(x - 2)}^2}}}{{{x^2}{{(x - 2)}^2}}}\\f\prime (x) = \frac{{2{x^2} - 4x + 3{x^2} - {x^2} + 4x - 4}}{{{x^2}{{(x - 2)}^2}}}\\f\prime (x) = \frac{{4{x^2} - 4}}{{{x^2}{{(x - 2)}^2}}} = 0 \Leftrightarrow x = \pm 1\end{array}\]
BBT:
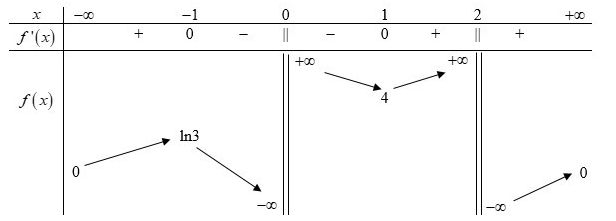
Dựa vào BBT ta thấy để phương trình có nghiệm duy nhất thì
\(\left[ {\begin{array}{*{20}{c}}{4m - 2020 = 0}\\{4m - 2020 = ln3}\\{4m - 2020 = 4}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 505}\\{m = \frac{{2020 + ln3}}{4}}\\{m = 506}\end{array}} \right. \notin \mathbb{Z}(ktm)\)
Vậy tổng các giá trị của m thỏa mãn yêu cầu bài toán là:\[505 + 506 = 1011\]Đáp án cần chọn là: B
Câu 27:
Đồ thị của hàm số y = f(x) đối xứng với đồ thị của hàm số \[y = {a^x}(a > 0,a \ne 1)\;\] qua điểm M(1;1). Giá trị của hàm số y = f(x) tại \[x = 2 + lo{g_a}\frac{1}{{2020\;}}\] bằng:
Lấy điểm \[A\left( {{x_0};{a^{{x_0}}}} \right) \in \left( {{C_1}} \right)\] (đồ thị của hàm số \[y = {a^x}\]. Gọi B là điểm đối xứng của A qua M(1;1).
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{x_B} = 2{x_M} - {x_A} = 2 - {x_0}}\\{{y_B} = 2{y_M} - {y_A} = 2 - {a^{{x_0}}}}\end{array}} \right. \Rightarrow {x_0} = 2 - {x_B} \Rightarrow {y_B} = 2 - {a^{2 - {x_B}}}\)
⇒ Hàm số\[y = f\left( x \right) = 2 - {a^{2 - x}}\]
\[ \Rightarrow f\left( {2 + {{\log }_a}\frac{1}{{2020}}} \right) = 2 - {a^{2 - \left( {2 + {{\log }_a}\frac{1}{{2020}}} \right)}}\]
\[ = 2 - {a^{{{\log }_a}20220}} = 2 - 2020 = - 2018\]
Đáp án cần chọn là: B
Câu 28:
Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị \[y = {\log _a}x,y = {\log _b}x\] và trục hoành lần lượt tại A,B và H phân biệt ta đều có 3HA=4HB (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
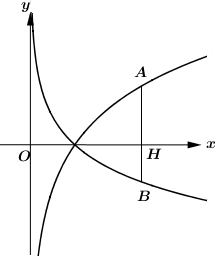
Gọi \[H\left( {{x_0};0} \right)\,\,\left( {{x_0} > 1} \right)\] ta có:\[A\left( {{x_0};{{\log }_a}{x_0}} \right);\,\,B\left( {{x_0};{{\log }_b}{x_0}} \right)\]
\[ \Rightarrow HA = {\log _a}{x_0};HB = - {\log _b}{x_0}\] (do\[{\log _a}{x_0} > 0,\,\,{\log _b}{x_0} < 0)\]
Theo bài ra ta có:\[3HA = 4HB \Leftrightarrow 3{\log _a}{x_0} = - 4{\log _b}{x_0}\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow 3{{\log }_a}{x_0} + 4{{\log }_b}{x_0} = 0}\\{ \Leftrightarrow \frac{3}{{{{\log }_{{x_0}}}a}} + \frac{4}{{{{\log }_{{x_0}}}b}} = 0}\\{ \Leftrightarrow \frac{{3{{\log }_{{x_0}}}b + 4{{\log }_{{x_0}}}a}}{{{{\log }_{{x_0}}}b.{{\log }_{{x_0}}}a}} = 0}\\{ \Leftrightarrow {{\log }_{{x_0}}}{b^3} + {{\log }_{{x_0}}}{a^4} = 0}\\{ \Leftrightarrow {{\log }_{{x_0}}}{a^4}{b^3} = 0}\\{ \Leftrightarrow {a^4}{b^3} = 1}\end{array}\]
Đáp án cần chọn là: D
Câu 29:
Cho hàm số \[f\left( x \right) = \ln \left( {{e^x} + m} \right)\]có \[f'\left( { - \ln 2} \right) = \frac{3}{2}\]. Mệnh đề nào dưới đây đúng?
Ta có: \[f\left( x \right) = \ln \left( {{e^x} + m} \right)\]
Điều kiện: \[{e^x} + m > 0.\]
\[\begin{array}{*{20}{l}}{ \Rightarrow f'\left( x \right) = \frac{{{e^x}}}{{{e^x} + m}}}\\{ \Rightarrow f'\left( { - \ln 2} \right) = \frac{3}{2} \Leftrightarrow \frac{{{e^{ - \ln 2}}}}{{{e^{ - \ln 2}} + m}} = \frac{3}{2}}\\{ \Leftrightarrow 2.{e^{ - \ln 2}} = 3.{e^{ - \ln 2}} + 3m}\\{ \Leftrightarrow {{2.2}^{ - \ln e}} = {{3.2}^{ - \ln e}} + 3m}\\{ \Leftrightarrow 2.\frac{1}{2} - 3.\frac{1}{2} = 3m}\\{ \Leftrightarrow m = - \frac{1}{6}.}\\{ \Rightarrow m \in \left( { - 2;\,\,0} \right).}\end{array}\]
Đáp án cần chọn là: A
Câu 30:
Xét các số thực a, b thỏa mãn a>b>1. Tìm giá trị nhỏ nhất Pmin của biểu thức \[P = \log _{\frac{a}{b}}^2\left( {{a^2}} \right) + 3{\log _b}\frac{a}{b}\].
Ta có \[P = \log _{\frac{a}{b}}^2\left( {{a^2}} \right) + 3{\log _b}\frac{a}{b}\]
\[ \Leftrightarrow P = 4\log _{\frac{a}{b}}^2a + 3\left( {{{\log }_b}a - 1} \right) \Leftrightarrow P = \frac{4}{{{{\left( {1 - {{\log }_a}b} \right)}^2}}} + 3\left( {\frac{1}{{{{\log }_a}b}} - 1} \right)\]
Đặt\[{\log _a}b = t \Rightarrow 0 < t < 1\] Khi đó \[P = \frac{4}{{{{\left( {t - 1} \right)}^2}}} + \frac{3}{t} - 3\]
\[P' = \frac{{ - 8}}{{{{\left( {t - 1} \right)}^3}}} - \frac{3}{{{t^2}}} = 0 \Leftrightarrow 3{t^3} - {t^2} + 9t - 3 = 0 \Rightarrow t = \frac{1}{3}\]
\[ \Rightarrow {P_{\min }} = 15\]
Đáp án cần chọn là: D
