Phương trình mũ và một số phương pháp giải
-
346 lượt thi
-
33 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phương trình \[{4^{2x + 5}} = {2^{2 - x}}\] có nghiệm là:
Đáp án cần chọn là: A
Câu 2:
Tổng các nghiệm của phương trình \[{3^{{x^4} - 3{x^2}}} = 81\]
\[{3^{{x^4} - 3{x^2}}} = 81 = {3^4} \Leftrightarrow {x^4} - 3{x^2} - 4 = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\]
Tổng các nghiệm sẽ bằng 0.
Đáp án cần chọn là: A
Câu 3:
Tìm nghiệm của phương trình \[\frac{{{3^{2x - 6}}}}{{27}} = {\left( {\frac{1}{3}} \right)^x}.\]
\[\frac{{{3^{2x - 6}}}}{{27}} = {\left( {\frac{1}{3}} \right)^x} \Leftrightarrow {3^{2x - 6}} = {3^3}{.3^{ - x}} \Leftrightarrow {3^{2x - 6}} = {3^{3 - x}} \Leftrightarrow 2x - 6 = 3 - x \Leftrightarrow x = 3\]
Đáp án cần chọn là: D
Câu 4:
Tìm nghiệm của phương trình \[{9^{\sqrt {x - 1} }} = {e^{\ln 81}}\]
\[{e^{\ln 81}} = 81 = {9^2}\]
Điều kiện:\[x \ge 1\]
Suy ra\[\sqrt {x - 1} = 2 \Leftrightarrow x - 1 = 4 \Rightarrow x = 5\]
Đáp án cần chọn là: A
Câu 5:
Giải phương trình \[{4^x} = {8^{x - 1}}\]
\[{4^x} = {8^{x - 1}} \Leftrightarrow {2^{2x}} = {2^{3\left( {x - 1} \right)}} \Leftrightarrow 2x = 3\left( {x - 1} \right) \Leftrightarrow x = 3\]
Đáp án cần chọn là: D
Câu 6:
Tìm tập hợp tất cả các nghiệm của phương trình \[{2^{{x^2} + x - 1}} = \frac{1}{2}\].
Đáp án cần chọn là: C
Câu 7:
Tìm giá trị của a để phương trình \[{(2 + \sqrt 3 )^x} + (1 - a){(2 - \sqrt 3 )^x} - 4 = 0\;\]có 2 nghiệm phân biệt thỏa mãn:\[{x_1} - {x_2} = lo{g_{2 + \sqrt 3 }}3\], ta có a thuộc khoảng:
Ta có \[{\left( {2 + \sqrt 3 } \right)^x}{\left( {2 - \sqrt 3 } \right)^x} = 1 \Rightarrow {\left( {2 - \sqrt 3 } \right)^x} = \frac{1}{{{{\left( {2 + \sqrt 3 } \right)}^x}}}\]
Đặt\[t = {\left( {2 + \sqrt 3 } \right)^x}\left( {t > 0} \right)\] phương trình đã cho trở thành
\[t + \frac{{1 - a}}{t} - 4 = 0 \Leftrightarrow {t^2} - 4t + 1 - a = 0\]
Phương trình đã cho có 2 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta = 3 + a > 0}\\{{t_1} + {t_2} = 4 > 0}\\{{t_1}{t_2} = 1 - a > 0}\end{array}} \right. \Leftrightarrow - 3 < a < 1\)
Ta có
\[{x_1} - {x_2} = {\log _{2 + \sqrt 3 }}3 \Leftrightarrow {\left( {2 + \sqrt 3 } \right)^{{x_1} - {x_2}}} = 3 \Leftrightarrow \frac{{{{\left( {2 + \sqrt 3 } \right)}^{{x_1}}}}}{{{{\left( {2 + \sqrt 3 } \right)}^{{x_2}}}}} = 3 \Leftrightarrow \frac{{{t_1}}}{{{t_2}}} = 3\]
Vì\[{t_1} + {t_2} = 4\] nên điều này xảy ra khi và chỉ khi phương trình (*) có 2 nghiệm t=3 và t=1.Khi đó\[1--a = 3.1 = 3 \Leftrightarrow a = --2\]
Trong 4 đáp án chỉ có B là đúng.
Đáp án cần chọn là: B
Câu 8:
Tính tổng T tất cả các nghiệm của phương trình\[{4.9^x} - {13.6^x} + {9.4^x} = 0\]
\[\begin{array}{l}{4.9^x} - {13.6^x} + {9.4^x} = 0 \Leftrightarrow 4 - 13.{\left( {\frac{2}{3}} \right)^x} + 9.{\left( {\frac{2}{3}} \right)^{2x}} = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\left( {\frac{2}{3}} \right)}^x} = 1}\\{{{\left( {\frac{2}{3}} \right)}^x} = \frac{4}{9}}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right. \Rightarrow T = 0 + 2 = 2\end{array}\]
Đáp án cần chọn là: A
Câu 9:
Tìm tập nghiệm S của phương trình: \[{4^{x + 1}} + {4^{x - 1}} = 272\]
Đáp án cần chọn là: B
Câu 10:
Giải phương trình \[\sqrt {{3^x} + 6} = {3^x}\]có tập nghiệm bằng:
Đặt
\[t = {3^x},t > 0 \Rightarrow \sqrt {t + 6} = t \to t + 6 = {t^2} \Rightarrow \left[ {\begin{array}{*{20}{c}}{t = - 2\left( l \right)}\\{t = 3}\end{array}} \right.\]
\[t = 3 \Rightarrow {3^x} = 3 \Rightarrow x = 1\]
Đáp án cần chọn là: C
Câu 11:
Tìm tích các nghiệm của phương trình \[{(\sqrt 2 - 1)^x} + {(\sqrt 2 + 1)^x} - 2\sqrt 2 = 0\]
Đặt\[t = {\left( {\sqrt 2 - 1} \right)^x}\left( {t > 0} \right)\] phương trình có dạng
\[t + \frac{1}{t} = 2\sqrt 2 \Leftrightarrow {t^2} - 2\sqrt 2 t + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = \sqrt 2 + 1\left( {tm} \right)}\\{t = \sqrt 2 - 1\left( {tm} \right)}\end{array}} \right.\]
Khi đó
\[\begin{array}{*{20}{l}}{t = \sqrt 2 + 1 \Rightarrow x = - 1}\\{t = \sqrt 2 - 1 \Rightarrow x = 1}\end{array}\]
Suy ra tích các nghiệm bằng −1.
Đáp án cần chọn là: B
Câu 12:
Tìm m để phương trình \[{4^x} - \;{2^{x\; + \;3}} + \;3\; = \;m\;\] có đúng 2 nghiệm \[x \in \left( {1;3} \right)\;\].
Đặt \[t = {2^x};x \in \left( {1;3} \right) \Rightarrow t = {2^x} \in \left( {2;8} \right)\]
Xét hàm số\[y = {t^2} - 8t + 3\] trên (2;8) có:
\[y' = 2t - 8;y' = 0 \Leftrightarrow 2t - 8 = 0 \Leftrightarrow t = 4 \in (2;8)\]
Bảng biến thiên:
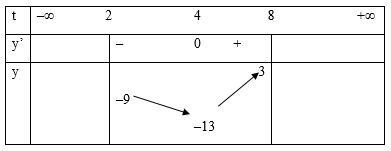
Căn cứ bảng biến thiên:
Phương trình \[{4^x} - {\rm{\;}}{2^{x{\rm{\;}} + {\rm{\;}}3}} + {\rm{\;}}3{\rm{\;}} = {\rm{\;}}m\] có đúng 2 nghiệm \[x \in \left( {1;3} \right) \Leftrightarrow - 13 < m < - 9\]
Đáp án cần chọn là: A
Câu 13:
Tìm tập hợp tất cả các tham số m sao cho phương trình \[{4^{{x^2} - 2x + 1}} - m{.2^{{x^2} - 2x + 2}} + 3m - 2 = 0\;\]có 4 nghiệm phân biệt.
Đặt \[t = {2^{{x^2} - 2x + 1}} \ge 1\]phương trình đã cho trở thành\[{t^2} - 2mt + 3m - 2 = 0\left( * \right)\]
Với t=1 ta tìm được 1 giá trị của x
Với t>1 ta tìm được 2 giá trị của x
Do đó, phương trình đã cho có 4 nghiệm phân biệt
⇔ Phương trình (*) có 2 nghiệm phân biệt lớn hơn 1
\(\left\{ {\begin{array}{*{20}{c}}{\Delta \prime = {m^2} - (3m - 2) > 0}\\{({t_1} - 1) + ({t_2} - 1) > 0}\\{({t_1} - 1)({t_2} - 1) > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{m^2} - (3m - 2) > 0}\\{{t_1} + {t_2} > 2}\\{{t_1}{t_2} - \left( {{t_1} + {t_2}} \right) + 1 > 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{m^2} - 3m + 2 > 0}\\{2m > 2}\\{3m - 2 - 2m + 1 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left[ {\begin{array}{*{20}{c}}{m > 2}\\{m < 1}\end{array}} \right.}\\{m > 1}\end{array}} \right. \Leftrightarrow m > 2\)</>
Đáp án cần chọn là: D
Câu 14:
Các giá trị thực của tham số m để phương trình : \[{12^x} + (4 - m){.3^x} - m = 0\;\] có nghiệm thuộc khoảng (−1;0) là:
- Từ các đáp án đã cho, ta thấy giá trị m=2 không thuộc đáp án C nên ta thử m=2 có thỏa mãn bài toán hay không sẽ loại được đáp án.
Thử với m=2 ta được phương trình : \[{12^x} + {2.3^x} - 2 = 0;f( - 1) = \frac{{ - 5}}{4};f(0) = 1\]
\[ \Rightarrow f(0).f( - 1) < 0\]
Do đó, phương trình có nghiệm trong khoảng (−1;0), mà đáp án C không chứa m=2 nên loại C.
- Lại có giá trị m=3 thuộc đáp án C nhưng không thuộc hai đáp án A và D nên nếu kiểm tra m=3 ta có thể loại tiếp được đáp án.
Thử với m=3 ta được phương trình : \[{12^x} + {3^x} - 3 = 0;f( - 1) = \frac{{ - 31}}{{12}};f(0) = - 1\]
\[ \Rightarrow f(0).f( - 1) > 0\]
Mà hàm số này đồng biến khi m=3 nên\[f(x) < 0,\forall x \in ( - 1;0)\]suy ra phương trình f(x)=0 sẽ không có nghiệm trong (−1;0), loại B.
- Cuối cùng, ta thấy giá trị m=1 thuộc đáp án A và không thuộc đáp án D nên ta sẽ thử m=1 để loại đáp án.
Thử với m=1 ta được phương trình :\[{12^x} + {3.3^x} - 1 = 0;f( - 1) = \frac{{ - 11}}{{12}};\,f(0) = 3 \Rightarrow f(0).f( - 1) < 0\]
Do đó phương trình f(x)=0 sẽ có nghiệm trong (−1;0) nên loại D và chọn A.
Đáp án cần chọn là: A
Câu 15:
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có 2 nghiệm phân biệt: \[{9^{1 - x}} + 2(m - 1){3^{1 - x}} + 1 = 0\]
Thử với m=−1 ta được phương trình:
\[{\left( {{3^{1 - x}}} \right)^2} - {4.3^{1 - x}} + 1 = 0\] phải có 2 nghiệm \[{3^{1 - x}}\] đều dương và 2 nghiệm đó là\[2 - \sqrt 3 \] và \[2 + \sqrt 3 \]
Vậy m=−1 thỏa mãn nên ta loại được A; B; D
Đáp án cần chọn là: C
Câu 16:
Tìm giá trị m để phương trình \[{2^{|x - 1| + 1}} + {2^{|x - 1|}} + m = 0\] có nghiệm duy nhất
Đặt \[\left| {x - 1} \right| = a\] khi đó phương trình trở thành\[{2^{a + 1}} + {2^a} + m = 0\](1)
Để phương trình đã cho có nghiệm duy nhất thì pt (1) bắt buộc phải có nghiệm duy nhất a=0 ( vì nếu a>0 thì sẽ tồn tại 2 giá trị của x)
Nên \[{2^1} + {2^0} + m = 0\]. Suy ra m=−3
Đáp án cần chọn là: C
Câu 17:
Cho số thực x thỏa mãn \[2 = {5^{lo{g_3}x}}\;\]. Mệnh đề nào sau đây đúng?
\[2 = {5^{{{\log }_3}x}} \Leftrightarrow {\log _5}2 = {\log _3}x \Leftrightarrow \frac{{{{\log }_5}x}}{{{{\log }_5}3}} = {\log _5}2\]
\[ \Leftrightarrow \frac{{{{\log }_5}x}}{{{{\log }_5}2}} = {\log _5}3 \Leftrightarrow {\log _5}3 = {\log _2}x \Leftrightarrow {\log _3}5 = {\log _x}2\]
Suy ra \[2 = {x^{{{\log }_3}5}}\]
Đáp án cần chọn là: C
Câu 18:
Biết phương trình \[{9^x} - {2^{x + \frac{1}{2}}} = {2^{x + \frac{3}{2}}} - {3^{2x - 1}}\]có nghiệm là a. Tính giá trị của biểu thức \[P = a + \frac{1}{2}lo{g_{\frac{9}{2}}}2\;\].
Phương trình trên tương đương với
\[{3^{2x - 2}} = {2^{x - \frac{3}{2}}} \Leftrightarrow {9^{x - 1}} = {2^{x - 1}}{.2^{\frac{{ - 1}}{2}}} \Leftrightarrow {(\frac{9}{2})^{x - 1}} = {2^{\frac{{ - 1}}{2}}}\]
\[ \Leftrightarrow x - 1 = {\log _{\frac{9}{2}}}{2^{\frac{{ - 1}}{2}}} \Leftrightarrow x = 1 - \frac{1}{2}{\log _{\frac{9}{2}}}2\]
Suy ra \[x + \frac{1}{2}{\log _{\frac{9}{2}}}2 = 1\]
Đáp án cần chọn là: C
Câu 19:
Biết rằng phương trình \[{2^{{x^2} - 1}} = {3^{x + 1}}\]có hai nghiệm là a và b. Khi đó a+b+ab có giá trị bằng
Lấy ln hai vế ta được:
\[({x^2} - 1)ln2 = (x + 1)ln3 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1}\\{(x - 1)ln2 = ln3}\end{array}} \right.\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1}\\{x - 1 = \frac{{ln3}}{{ln2}} = lo{g_2}3}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1}\\{x = 1 + lo{g_2}3}\end{array}} \right.\)
Nếu\[a = - 1;b = 1 + lo{g_2}3 \Rightarrow a + b + ab = \; - 1\]
Đáp án cần chọn là: C
Câu 20:
Tìm các giá trị m để phương trình \[{2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3\;}}\]luôn thỏa, \[\forall x \in R\].
\[{2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3}} \Leftrightarrow {2^{x + 1}} = m{.2^{x + 1 + 1}} - {2^{x + 1 + 2}}\]
\[ \Leftrightarrow {2^{x + 1}} = m{.2.2^{x + 1}} - {2^2}{.2^{x + 1}} \Leftrightarrow {2^{x + 1}} = (2m - 4){2^{x + 1}}\]
\[ \Leftrightarrow 2m - 4 = 1 \Leftrightarrow m = \frac{5}{2}\]
Đáp án cần chọn là: A
Câu 21:
Số nghiệm thực phân biệt của phương trình \[{4^{{x^2}}} - {5.2^{{x^2}}} + 4 = 0\] là
\[{4^{{x^2}}} - {5.2^{{x^2}}} + 4 = 0 \Leftrightarrow {({2^{{x^2}}})^2} - {5.2^{{x^2}}} + 4 = 0\]
\[ \Leftrightarrow ({2^{{x^2}}} - 4)({2^{{x^2}}} - 1) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{2^{{x^2}}} = 4}\\{{2^{{x^2}}} = 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^2} = 2}\\{{x^2} = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \pm \sqrt 2 }\\{x = 0}\end{array}} \right.\)
Đáp án cần chọn là: A
Câu 22:
Trong các phương trình sau đây, phương trình nào có nghiệm?
Ý A: Điều kiện x > 0. Có \[{x^{\frac{2}{3}}} + 5 > 0,\forall x > 0\] nên phương trình vô nghiệm
Ý B: Điều kiện x > 4. Có \[{\left( {3x} \right)^{\frac{1}{3}}} + {\left( {x - 4} \right)^{\frac{2}{3}}} > 0,\forall x > 4\] nên phương trình vô nghiệm
Ý C: Điều kiện \[x \ge 2\]. Có \[\sqrt {4x - 8} + 2 > 0,\forall x \ge 2\]nên phương trình vô nghiệm
Ý D: Điều kiện x > 0. Có \[2{x^{\frac{1}{2}}} - 3 = 0 \Leftrightarrow {x^{\frac{1}{2}}} = \frac{3}{2} \Leftrightarrow x = {\log _{\frac{1}{2}}}\frac{3}{2}\] (thỏa mãn)
Đáp án cần chọn là: D
Câu 23:
Số nghiệm thực phân biệt của phương trình \[{2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} = 4\]là:
Điều kiện : \[x \ne 0\]
Với x<0 ta có\(\left\{ {\begin{array}{*{20}{c}}{x + \frac{1}{{4x}} < 0}\\{\frac{x}{4} + \frac{1}{x} < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{2^{x + \frac{1}{{4x}}}} < 1}\\{{2^{\frac{x}{4} + \frac{1}{x}}} < 1}\end{array}} \right. \Rightarrow {2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} < 2\)
⇒ Phương trình không có nghiệm x<0
Với x > 0, áp dụng bất đẳng thức Côsi cho hai số dương ta được.
\(\left\{ {\begin{array}{*{20}{c}}{x + \frac{1}{{4x}} \ge 2\sqrt {x.\frac{1}{{4x}}} = 1}\\{\frac{x}{4} + \frac{1}{x} \ge 2\sqrt {\frac{x}{4}.\frac{1}{x}} = 1}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{2^{x + \frac{1}{{4x}}}} \ge 2}\\{{2^{\frac{x}{4} + \frac{1}{x}}} \ge 2}\end{array}} \right. \Rightarrow {2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} \ge 4\)
Dấu “=” xảy ra khi và chỉ khi\(\left\{ {\begin{array}{*{20}{c}}{x = \frac{1}{{4x}}}\\{\frac{x}{4} = \frac{1}{x}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4{x^2} = 1}\\{{x^2} = 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x^2} = \frac{1}{4}}\\{{x^2} = 4}\end{array}} \right.\)(không xảy ra)
Vậy \[{2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} > 4\]nên phương trình vô nghiệm
Đáp án cần chọn là: D
Câu 24:
Phương trình \[x({2^{x - 1}} + 4) = {2^{x + 1}} + {x^2}\]có tổng các nghiệm bằng
\[x({2^{x - 1}} + 4) = {2^{x + 1}} + {x^2} \Leftrightarrow x{.2^{x - 1}} - {4.2^{x - 1}} + 4x - {x^2} = 0\]
\[ \Leftrightarrow (x - 4)({2^{x - 1}} - x) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 4}\\{{2^{x - 1}} - x = 0( * )}\end{array}} \right.\)
Xét hàm số \[f\left( x \right) = {2^{x - 1}} - x\] trên\(\mathbb{R}\). Ta có
\[f'\left( x \right) = {2^{x - 1}}\ln 2 - 1 = 0 \Leftrightarrow x = {x_0} = 1 + {\log _2}\left( {\frac{1}{{\ln 2}}} \right)\]
\[f'\left( x \right) < 0 \Leftrightarrow x < {x_0};f'\left( x \right) > 0 \Leftrightarrow x > {x_0}\]</>
nên phương trình\[f(x) = 0\]có tối đa 1 nghiệm trong các khoảng\[\left( { - \infty ;{x_0}} \right)\]và\[\left( {{x_0}; + \infty } \right)\]
Mà \[f\left( 1 \right) = f\left( 2 \right) = 0\]nên phương trình (*) có 2 nghiệm x=1 và x=2
Tổng các nghiệm của phương trình đã cho là 7.
Đáp án cần chọn là: A
Câu 25:
Cho aa là số thực dương, khác 1 và thỏa mãn \[\frac{1}{2}({a^\alpha } + {a^{ - \alpha }}) = 1\;\]. Tìm \[\alpha \]
Áp dụng bất đẳng thức Cauchy ta có .
Dấu "=" xảy ra khi \[{a^\alpha } = {a^{ - \alpha }}\]. Điều này dẫn đến \[\alpha = - \alpha \Rightarrow \alpha = 0\]
Đáp án cần chọn là: C
Câu 26:
Phương trình \[{2^{23{x^3}}}{.2^x} - {1024^{{x^2}}} + 23{x^3} = 10{x^2} - x\] có tổng các nghiệm gần nhất với số nào dưới đây:
\[{2^{23{x^3}}}{.2^x} - {1024^{{x^2}}} + 23{x^3} = 10{x^2} - x \Leftrightarrow {2^{23{x^3} + x}} + 23{x^3} + x = {2^{10{x^2}}} + 10{x^2}\]
Xét hàm số\[f(t) = {2^t} + t;f'(t) = {2^t}\ln 2 + 1 > 0,\forall t\]
\[ \Rightarrow f(23{x^3} + x) = f(10{x^2}) \Leftrightarrow 23{x^3} + x = 10{x^2} \Leftrightarrow x(23{x^2} - 10x + 1) = 0\]
Theo vi-et cho phương trình bậc 3 ta có \[{x_1} + {x_2} + {x_3} = - \frac{b}{a} = \frac{{10}}{{23}} \approx 0,45\]
Đáp án cần chọn là: D
Câu 27:
Tìm tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất \[1 + \left[ {2{x^2} - m\left( {m + 1} \right)x - 2} \right]{.2^{1 + mx - {x^2}}} = \left( {{x^2} - mx - 1} \right){.2^{mx\left( {1 - m} \right)}} + {x^2} - {m^2}x\].
Ta có:
\[1 + \left[ {2{x^2} - m\left( {m + 1} \right)x - 2} \right]{.2^{1 + mx - {x^2}}} = \left( {{x^2} - mx - 1} \right){.2^{mx\left( {1 - m} \right)}} + {x^2} - {m^2}x\]
\[ \Leftrightarrow \left[ {\left( {{x^2} - {m^2}x - 1} \right) + \left( {{x^2} - mx - 1} \right)} \right]{.2^{ - \left( {{x^2} - mx - 1} \right)}} = \left( {{x^2} - mx - 1} \right){.2^{\left( {{x^2} - {m^2}x - 1} \right) - \left( {{x^2} - mx - 1} \right)}} + {x^2} - {m^2}x - 1\]
Đặt\(\left\{ {\begin{array}{*{20}{c}}{u = {x^2} - {m^2}x - 1}\\{v = {x^2} - mx - 1}\end{array}} \right.\) Phương trình trở thành:
\[\left( {u + v} \right){.2^{ - v}} = v{.2^{u - v}} + u \Leftrightarrow u\left( {{2^{ - v}} - 1} \right) = v{2^{ - v}}\left( {{2^u} - 1} \right)\left( * \right)\]
+) Dễ dàng kiểm tra u=0 hoặc v=0 là nghiệm của (*)
+) Với \[u,v \ne 0,\left( * \right) \Leftrightarrow \frac{{{2^{ - v}} - 1}}{{v{2^{ - v}}}} = \frac{{{2^u} - 1}}{u}\]
\[ \Leftrightarrow \frac{{{2^u} - 1}}{u} = \frac{{1 - {2^v}}}{v}\]
\[ \Leftrightarrow \frac{{{2^u} - 1}}{u} + \frac{{{2^v} - 1}}{v} = 0\]
Xét hàm\[f\left( t \right) = \frac{{{2^t} - 1}}{t}\] trên\[\mathbb{R} \setminus \left\{ 0 \right\}\] ta thấy:
+) Với t>0 thì\(\left\{ {\begin{array}{*{20}{c}}{{2^t} - 1 > 0}\\{t > 0}\end{array}} \right. \Rightarrow \frac{{{2^t} - 1}}{t} > 0 \Rightarrow f\left( t \right) > 0\)
+) Với t<0 thì \(\left\{ {\begin{array}{*{20}{c}}{{2^t} - 1 < 0}\\{t < 0}\end{array}} \right. \Rightarrow \frac{{{2^t} - 1}}{t} > 0 \Rightarrow f\left( t \right) > 0\)</0 thì>
Do đó \[f\left( t \right) > 0\] với mọi \[t \ne 0\]
\[ \Rightarrow f\left( u \right) > 0,f\left( v \right) > 0,\forall u,v \ne 0\]
\[ \Rightarrow f\left( u \right) + f\left( v \right) > 0,\forall u,v \ne 0\]
\[ \Rightarrow \frac{{{2^u} - 1}}{u} + \frac{{{2^v} - 1}}{v} > 0,\forall u,v \ne 0\]
Do đó phương trình\[\frac{{{2^u} - 1}}{u} + \frac{{{2^v} - 1}}{v} = 0\] vô nghiệm.
Vậy \(\left[ {\begin{array}{*{20}{c}}{u = 0}\\{v = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^2} - {m^2}x - 1 = 0(1)}\\{{x^2} - mx - 1 = 0(2)}\end{array}} \right.\)
Hai phương trình trên luôn có hai nghiệm phân biệt, tổng hai nghiệm ở mỗi phương trình là:
\[{S_1} = {m^2},\,{S_2} = m \Rightarrow S = {m^2} + m \ge - \frac{1}{4}\]
Vậy tổng các nghiệm của phương trình đã cho nhỏ nhất là \[ - \frac{1}{4}\] khi \[m = - \frac{1}{2}\]Đáp án cần chọn là: C
Câu 28:
Cho hàm số y=f(x) có bảng biến thiên như sau
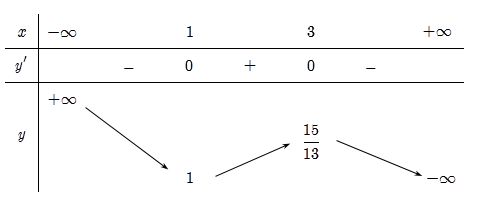
Biết f(0)=76, giá trị lớn nhất của mm để phương trình \[{e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m\] có nghiệm trên đoạn \[\left[ {0;2} \right]\;\]là
Ta có:
\[{e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m \Leftrightarrow 2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2} = \ln m\]
Xét \[g\left( x \right) = 2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}\]có:
\[g'\left( x \right) = 6{f^2}\left( x \right)f'\left( x \right) - 13f\left( x \right)f'\left( x \right) + 7f'\left( x \right) = f'\left( x \right)\left[ {6{f^2}\left( x \right) - 13f\left( x \right) + 7} \right]\]
Suy ra
\[g\prime (x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{f\prime (x) = 0}\\{6{f^2}(x) - 13f(x) + 7 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{f\prime (x) = 0}\\{f(x) = 1}\\{f(x) = \frac{7}{6}}\end{array}} \right.\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1;x = 3}\\{x = 1,x = {x_1} > 3}\\{x = {x_2} < 1}\end{array}} \right.\)
Xét g(x) trên đoạn \[[0;2].\]
+ Trong khoảng (0;1) thì\[f'\left( x \right) < 0,f\left( x \right) > 1,f\left( x \right) < f(0) = \frac{7}{6}\]nên\[f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \frac{7}{6}} \right) > 0\]hay\[g'\left( x \right) > 0\]</></>
+ Trong khoảng (1;2) thì \[f'\left( x \right) > 0,f\left( x \right) > 1,f\left( x \right) < \frac{{15}}{{13}} < \frac{7}{6}\]nên\[f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \frac{7}{6}} \right) < 0\]hay \[g'\left( x \right) < 0\]
Từ đó ta có bảng biến thiên của g(x) như sau:
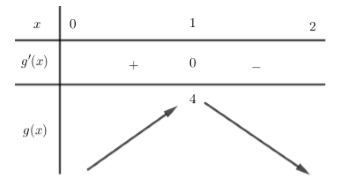
Từ bảng biến thiên ta thấy \[\mathop {\max }\limits_{\left[ {0;2} \right]} g\left( x \right) = 4\]
Vậy yêu cầu bài toán thỏa nếu và chỉ nếu\[\ln m \le 4 \Leftrightarrow m \le {e^4}\]hay giá trị lớn nhất của m là \[m = {e^4}\].
Đáp án cần chọn là: A
Câu 29:
Cho các số thực không âm x,y,z thỏa mãn \[{5^x} + {25^y} + {125^z} = 2020\]. Giá trị nhỏ nhất của biếu thức \[T = \frac{x}{6} + \frac{y}{3} + \frac{z}{2}\] là
Đặt \(\left\{ {\begin{array}{*{20}{c}}{a = {5^x}}\\{b = {5^{2y}}}\\{c = {5^{3z}}}\end{array}} \right.\) với\[x,\,\,y,\,\,z \ge 0\] thì\[a,\,\,b,\,\,c \ge 1\]
Theo bài ra ta có\[a + b + c = 2020 \Rightarrow 1 \le a,b,c \le 2018\]
Ta có:
\[(a - 1)(b - 1)(c - 1) \ge 0\]
\[ \Leftrightarrow (ab - a - b + 1)(c - 1) \ge 0\]
\[ \Leftrightarrow abc + (a + b + c) - (ab + bc + ca) - 1 \ge 0(1)\]
\[(a - 2018)(b - 2018)(c - 2018) \le 0\]
\[ \Leftrightarrow (ab - 2018(a + b) + 20182)(c - 2018) \le 0\]
\[ \Leftrightarrow abc + {2018^2}(a + b + c) - 2018(ab + bc + ca) - {2018^3} \le 0(2)\]
Lấy (1) nhân với 2018 rồi trừ đi (2) ta được:
\[2017abc + (2018 - {2018^2})(a + b + c) - 2018 + {2018^3} \ge 0\]
\[ \Leftrightarrow 2017abc + 2018(1 - 2018)(a + b + c) + {2018^3} - 2018 \ge 0\]
\[ \Leftrightarrow 2017abc - 2017.2018.(a + b + c) + {2018^3} - 2018 \ge 0\]
\[ \Leftrightarrow {2017.5^x}{.5^{2y}}{.5^{3z}} - 2017.2018.2020 + {2018^3} - 2018 \ge 0\]
\[ \Leftrightarrow {2017.5^x}{.5^{2y}}{.5^{3z}} + 2018({2018^2} - 2017.2020 - 1) \ge 0\]
\[ \Leftrightarrow {2017.5^x}{.5^{2y}}{.5^{3z}} - 2017.2018 \ge 0\]
\[ \Leftrightarrow {5^x}{.5^{2y}}{.5^{3z}} - 2018 \ge 0\]
\[ \Leftrightarrow {5^x}{.5^{2y}}{.5^{3z}} \ge 2018\]
\[ \Leftrightarrow {5^{x + 2y + 3z}} \ge 2018\]
\[ \Leftrightarrow x + 2y + 3z \ge lo{g_5}2018\]
\[ \Leftrightarrow \frac{{x + 2y + 3z}}{6} \ge \frac{1}{6}lo{g_5}2018\]
\[ \Leftrightarrow \frac{x}{6} + \frac{y}{3} + \frac{z}{2} \ge \frac{1}{6}lo{g_5}2018\]
Vậy giá trị nhỏ nhất của biểu tức \[T = \frac{x}{6} + \frac{y}{3} + \frac{z}{2}\] là\[\frac{1}{6}{\log _5}2018\]
Đáp án cần chọn là: B
Câu 30:
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình \[{16^x} - {2.12^x} + \left( {m - 2} \right){.9^x} = 0\]có nghiệm dương?
Ta có\[{16^x} - {2.12^x} + \left( {m - 2} \right){.9^x} = 0\] (1)
\[ \Leftrightarrow {\left( {\frac{4}{3}} \right)^{2x}} - 2.{\left( {\frac{4}{3}} \right)^x} + m - 2 = 0\] chia cả hai vế cho\[{9^x}\]
Đặt\[{\left( {\frac{4}{3}} \right)^x} = t \Rightarrow x = {\log _{\frac{4}{3}}}t > 0 \Leftrightarrow t > 1\]
Khi đó ta có phương trình \[{t^2} - 2t + m - 2 = 0\left( * \right)\]
Để phương trình (1) có nghiệm dương thì phương trình (*) có nghiệm lớn hơn 1.
(*) có nghiệm\[ \Leftrightarrow {\rm{\Delta '}} = 1 - m + 2 \ge 0 \Leftrightarrow 3 - m \ge 0 \Leftrightarrow m \le 3\]
Với \[m \le 3\] thì (∗) có nghiệm \[{t_1} = 1 - \sqrt {3 - m} ,{t_2} = 1 + \sqrt {3 - m} \]
Để (*) có nghiệm lớn hơn 1 thì
\[1 + \sqrt {3 - m} > 1 \Leftrightarrow \sqrt {3 - m} > 0 \Leftrightarrow 3 - m > 0 \Leftrightarrow m < 3\]
Mà m nguyên dương nên \[m \in \left\{ {1;2} \right\}\]Vậy có 2 giá trị của mm thỏa mãn.
Đáp án cần chọn là: B
Câu 31:
Cho \[{4^x} + {4^{ - x}} = 7\]. Khi đó biểu thức \[P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + {{4.2}^x} + {{4.2}^{ - x}}}} = \frac{a}{b}\] với \[\frac{a}{b}\] tối giản và \[a,b \in \mathbb{Z}\]. Tích a.b có giá trị bằng
\[\begin{array}{*{20}{l}}{{4^x} + {4^{ - x}} = 7}\\{{4^x} + {4^{ - x}} + 2 = 9}\\{ \Leftrightarrow {{\left( {{2^x}} \right)}^2} + {{\left( {{2^{ - x}}} \right)}^2} + {{2.2}^x}{{.2}^{ - x}} = 9}\\{ \Leftrightarrow {{\left( {{2^x} + {2^{ - x}}} \right)}^2} = 9}\\{ \Leftrightarrow {2^x} + {2^{ - x}} = 3}\end{array}\]
(do \[{2^x} + {2^{ - x}} > 0\])
Vậy
\[\begin{array}{*{20}{l}}{P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + {{4.2}^x} + {{4.2}^{ - x}}}}}\\{\,\,\,\, = \frac{{5 - \left( {{2^x} + {2^{ - x}}} \right)}}{{8 + 4\left( {{2^x} + {2^{ - x}}} \right)}}}\\{\,\,\,\, = \frac{{5 - 3}}{{8 + 4.3}} = \frac{1}{{10}}}\\{ \Rightarrow a = 1,b = 10 \Rightarrow a.b = 1.10 = 10}\end{array}\]
Đáp án cần chọn là: A
Câu 32:
Đề thi THPT QG - 2021 - mã 101
Có bao nhiêu số nguyên y sao cho tồn tại \[x \in (\frac{1}{3};3)\;\] thỏa mãn \[27{\,^{3{x^2} + xy}} = \left( {1 + xy} \right){27^{9x}}\]?
* pt \[ \Leftrightarrow 27{\,^{3{x^2} + xy - 9x}} = xy + 1\]
\[ \Rightarrow xy + 1 > 0 \Leftrightarrow y > - \frac{1}{x}khix \in \left( {\frac{1}{3};3} \right) \Rightarrow y > - 3\] thì mới tồn tại\[x \in \left( {\frac{1}{3};3} \right)\]
⇒ Ta chặn được\[y > - 3 \Rightarrow y \ge - 2\]
\[*pt \Leftrightarrow {27^{3{x^2} + xy - 9x}} - xy - 1 = 0\]
Đặt \[f\left( x \right) = g\left( y \right) = {27^{3{x^2} + xy - 9x}} - xy - 1\] ta có\(\left\{ {\begin{array}{*{20}{c}}{f(\frac{1}{3}) = {3^{y - 8}} - \frac{y}{3} - 1}\\{f(3) = {{27}^{3y}} - 3y - 1}\end{array}} \right.\)
Nhận thấy ngay\[f\left( 3 \right) \ge 0\,\,\forall y \in \mathbb{Z}\] chỉ bằng 0 tại y=0
+ Xét y=0⇒ thay vào phương trình ban đầu ⇒\(\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 3}\end{array}} \right.\) loại vì không có nghiệm thuộc \[\left( {\frac{1}{3};3} \right)\]
+ Xét\[y \ne 0 \Rightarrow f\left( 3 \right) > 0\,\,\forall x \in {\mathbb{Z}^ * }\]
1) Ta Table khảo sát\[f\left( {\frac{1}{3}} \right)\] với\(\left\{ {\begin{array}{*{20}{c}}{Start:y = - 2}\\{End:y = 17}\\{Step: = 1}\end{array}} \right.\)
\[ \Rightarrow f\left( {\frac{1}{3}} \right) < 0\,\,\forall y \in \left\{ { - 2; - 1;1;2;...;9} \right\}\]
\[ \Rightarrow f\left( {\frac{1}{3}} \right).f\left( 3 \right) < 0\,\,\forall y \in \left\{ { - 2; - 1;1;2;...;9} \right\}\]
⇒ Có 11 giá trị của yy để tồn tại nghiệm
2) Từ bảng Table ta nhận thấy khi\[y \ge 10\] thì \[f\left( {\frac{1}{3}} \right) > 0\] và đồng biến.
Ta đi chứng minh khi \[y \ge 10\] thì phương trình vô nghiệm.
\[g\prime (y) = x({27^{3{x^2} + x(y - 9)}}.ln27 - 1) > 0\left\{ {\begin{array}{*{20}{c}}{\forall y \ge 10}\\{x \in \left( {\frac{1}{3};3} \right)}\end{array}} \right.\]
\[ \Rightarrow g\left( y \right) \ge g\left( {10} \right) = {27^{3{x^2} + x}} - 10x - 1 = h\left( x \right)\]
Ta có\[h'\left( x \right) = {27^{3{x^2} + x}}\left( {6x + 1} \right)\ln 27 - 10 > 0\,\,\forall x \in \left( {\frac{1}{3};3} \right)\]
\[ \Rightarrow h\left( x \right) > h\left( {\frac{1}{3}} \right) = \frac{{14}}{3} > 0\]
⇒ Phương trình vô nghiệm với\[x \in \left( {\frac{1}{3};3} \right)\]Vậy đáp số có 11 giá trị nguyên của yy.
Đáp án cần chọn là: C
Câu 33:
Cho các số dương x,y thỏa mãn \[{2^{{x^3} - y + 1}} = \frac{{2x + y}}{{2{x^3} + 4x + 4}}\]. Giá trị nhỏ nhất của biểu thức \[P = \frac{7}{y} + \frac{{{x^3}}}{7}\] có dạng \(\frac{a}{b}\). Tính a−b.
Bước 1: Sử dụng hàm đặc trưng, tìm biểu diễn \[{x^3}\] theo y.
Ta có\[{2^{{x^3} - y + 1}} = \frac{{2x + y}}{{2{x^3} + 4x + 4}}\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow {2^{{x^3} + 2x + 2 - 2x - y - 1}} = \frac{{2x + y}}{{2{x^3} + 4x + 4}}}\\{ \Leftrightarrow \frac{{{2^{{x^3} + 2x + 2}}}}{{{2^{2x + y}}.2}} = \frac{{2x + y}}{{2\left( {{x^3} + 2x + 2} \right)}}}\\{ \Leftrightarrow {2^{{x^3} + 2x + 2}}\left( {{x^3} + 2x + 2} \right) = {2^{2x + y}}.\left( {2x + y} \right)\,\,\,\left( * \right)}\end{array}\]
Xét \[f\left( t \right) = {2^t}.t,\,\,t > 0\]ta có\[f'\left( t \right) = {2^t} + t{.2^t}.\ln 2 > 0;\,\,\forall t > 0\].Do đó hàm số f(t) đồng biến trên \[\left( {0; + \infty } \right)\]Do đó \[\left( * \right) \Leftrightarrow {x^3} + 2x + 2 = 2x + y \Rightarrow {x^3} = y - 2\]Bước 2: Thế vào biểu thức P, sử dụng BĐT Cô-si tìm GTNN của biểu thức P.
Khi đó
\[P = \frac{7}{y} + \frac{{{x^3}}}{7} = \frac{7}{y} + \frac{{y - 2}}{7} = \frac{7}{y} + \frac{y}{7} - \frac{2}{7} \ge 2\sqrt {\frac{7}{y}.\frac{y}{7}} - \frac{2}{7} = \frac{{12}}{7}\]
Dấu “=” xảy ra \[ \Leftrightarrow \frac{7}{y} = \frac{y}{7} \Leftrightarrow y = 7\,\,\left( {do\,\,y > 0} \right)\]
\[{P_{\min }} = \frac{{12}}{7} \Leftrightarrow x = \sqrt[3]{5},\,\,y = 7\]
Vậy\[a = 12,b = 7 = > a - b = 5\]
