Ứng dụng tích phân để tính diện tích
-
335 lượt thi
-
27 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), đường thẳng y=0 và hai đường thẳng \[x = a,x = b(a < b)\] là:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số\[y = f\left( x \right)\] đường thẳng y=0 và hai đường thẳng\[x = a,x = b\] là\[S = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\]
Đáp án cần chọn là: D
Câu 2:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right) = {x^2} - 1\], trục hoành và hai đường thẳng x=−1;x=−3 là:
Đáp án cần chọn là: A
Câu 3:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right),y = g\left( x \right)\] và hai đường thẳng \[x = a,x = b(a < b)\;\] là:
Đáp án cần chọn là: C
Câu 4:
Cho hai hàm số \[f(x) = - x\;\] và \[g(x) = {e^x}\]. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \[y = f(x),y = g(x)\;\] và hai đường thẳng x=0,x=e là:
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số\[y = f\left( x \right),y = g\left( x \right)\] và hai đường thẳng \[x = 0,x = e\] là:
\[S = \mathop \smallint \limits_0^e \left| {{e^x} - \left( { - x} \right)} \right|dx = \mathop \smallint \limits_0^e \left| {{e^x} + x} \right|dx\]
Đáp án cần chọn là: A
Câu 5:
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \[y = {x^3} - x;y = 2x\] và các đường thẳng \[x = - 1;x = 1\;\] được xác định bởi công thức:
Xét phương trình hoành độ giao điểm của 2 đồ thị:
\[{x^3} - x = 2x \Leftrightarrow {x^3} - 3x = 0 \Leftrightarrow x = 0\] (chỉ xét trên\[\left( { - 1;1} \right)\]
Với\[x \in \left( { - 1;0} \right)\] thì\[{x^3} - 3x > 0\] với \[x \in \left( {0;1} \right)\] thì \[{x^3} - 3x < 0\]
Diện tích cần tìm là \[S = \mathop \smallint \limits_{ - 1}^1 \left| {{x^3} - 3x} \right|dx = \mathop \smallint \limits_{ - 1}^0 \left( {{x^3} - 3x} \right)dx + \mathop \smallint \limits_0^1 \left( {3x - {x^3}} \right)dx\]
Đáp án cần chọn là: D
Câu 6:
Tìm diện tích hình phẳng giới hạn bởi các đường \[y = (x - 1){e^x}\], trục hoành, đường thẳng x=0 và x=1
Diện tích cần tính là\[S = \mathop \smallint \limits_0^1 \left| {\left( {x - 1} \right){e^x}} \right|dx = \mathop \smallint \limits_0^1 \left( {1 - x} \right){e^x}dx = 0,718... = e - 2\]
(sử dụng máy, tính trực tiếp và so sánh với các đáp án)
Đáp án cần chọn là: C
Câu 7:
Gọi SS là diện tích hình phẳng (H) giới hạn bởi các đường y=f(x), trục hoành và hai đường thẳng x=−1,x=2 (như hình vẽ). Đặt \[a = \mathop \smallint \limits_{ - 1}^0 f(x)dx,b = \mathop \smallint \limits_0^2 f(x)dx\]. Mệnh đề nào sau đây đúng?
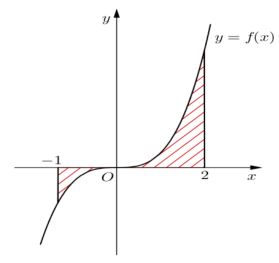
Diện tích hình phẳng là \[\mathop \smallint \limits_{ - 1}^2 \left| {f(x)} \right|dx\]
Dựa vào hình vẽ ta có được:
\[S = \mathop \smallint \limits_{ - 1}^0 (0 - f(x))dx + \mathop \smallint \limits_0^2 f(x)dx = - \mathop \smallint \limits_{ - 1}^0 f(x)dx + \mathop \smallint \limits_0^2 f(x)dx = b - a\]
Đáp án cần chọn là: A
Câu 8:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số \[y = {x^2} - 4\;\] và \[y = x - 4\]
Xét phương trình :\[{x^2} - 4 = x - 4 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 1}\end{array}} \right.\]
Trong khoảng (0;1) thì \[{x^2} - x < 0\]
Diện tích cần tìm là :
\[S = \mathop \smallint \limits_0^1 \left| {{x^2} - 4 - x + 4} \right|dx = \mathop \smallint \limits_0^1 \left| {{x^2} - x} \right|dx = - \mathop \smallint \limits_0^1 \left( {{x^2} - x} \right)dx = \frac{1}{6}\]
Đáp án cần chọn là: C
Câu 9:
Diện tích hình phẳng giới hạn bởi nửa đường tròn \[{x^2} + {y^2} = 2,y > 0\] và parabol \[y = {x^2}\;\] bằng:
\[{x^2} + {y^2} = 2(y > 0) \Leftrightarrow y = \sqrt {2 - {x^2}} \]
+ Hoành độ giao điểm của 2 đường là nghiệm của phương trình:
\(\sqrt {2 - {x^2}} = {x^2} \Leftrightarrow {x^4} + {x^2} - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^2} = 1}\\{{x^2} = - 2\left( L \right)}\end{array}} \right.\)
\[ \Leftrightarrow x = \pm 1\]
+ Với \[ - 1 \le x \le 1\] thì
\[\begin{array}{*{20}{l}}{{x^2} \le 1 \Rightarrow {x^4} \le 1}\\{ \Rightarrow {x^4} + {x^2} - 2 = \left( {{x^4} - 1} \right) + \left( {{x^2} - 1} \right) \le 0}\end{array}\]
\[\begin{array}{*{20}{l}}{ \Rightarrow 0 \le {x^4} \le 2 - {x^2}}\\{ \Rightarrow {x^2} \le \sqrt {2 - {x^2}} }\end{array}\]
\[ \Rightarrow {x^2} - \sqrt {2 - {x^2}} \le 0 \Rightarrow \left| {\sqrt {2 - {x^2}} - {x^2}} \right| = \sqrt {2 - {x^2}} - {x^2}\]
+ Diện tích hình phẳng là:
\[S = \mathop \smallint \limits_{ - 1}^1 \left| {\sqrt {2 - {x^2}} - {x^2}} \right|dx = \mathop \smallint \limits_{ - 1}^1 \left( {\sqrt {2 - {x^2}} - {x^2}} \right)dx = \mathop \smallint \limits_{ - 1}^1 \sqrt {2 - {x^2}} dx - \mathop \smallint \limits_{ - 1}^1 {x^2}dx\]
+ Với\[{I_1} = \mathop \smallint \limits_{ - 1}^1 \sqrt {2 - {x^2}} dx\]
Đặt\[x = \sqrt 2 \sin u \Rightarrow dx = \sqrt 2 \cos udu\]
Khi\[x = - 1 \Rightarrow u = - \frac{\pi }{4}\]
\[x = 1 \Rightarrow u = \frac{\pi }{4}\]
Do đó \[{I_1} = \mathop \smallint \limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} \sqrt {2 - 2{{\sin }^2}u} .\sqrt 2 \cos udu = \mathop \smallint \limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} 2{\cos ^2}udu = \mathop \smallint \limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} (1 + \cos 2u)du\]
\( = u\left| {_{ - \frac{\pi }{4}}^{\frac{\pi }{4}}} \right. + \frac{1}{2}sin2u\left| {_{ - \frac{\pi }{4}}^{\frac{\pi }{4}}} \right. = \frac{\pi }{4} + \frac{\pi }{4} + \frac{1}{2}sin\frac{\pi }{2} - \frac{1}{2}\sin \left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2} + 1\)
+ Với\({I_2} = \int\limits_{ - 1}^1 {{x^2}dx = } \frac{1}{3}{x^3}\left| {_{ - 1}^1} \right. = \frac{1}{3} + \frac{1}{3} = \frac{2}{3}\)
\[ \Rightarrow S = {I_1} - {I_2} = \frac{\pi }{2} + 1 - \frac{2}{3} = \frac{\pi }{2} + \frac{1}{3}\]
Đáp án cần chọn là: D
Câu 10:
Gọi S là diện tích hình phẳng giới hạn bởi các đường \[y = {x^3},y = 2 - x\]và y = 0. Mệnh đề nào sau đây là đúng?
A.\[S = \mathop \smallint \limits_0^1 {x^3}d{\rm{x}} + \mathop \smallint \limits_1^2 \left( {x - 2} \right)d{\rm{x}}\]
Phương trình hoành độ giao điểm của các đồ thị là:\(\left\{ {\begin{array}{*{20}{c}}{2 - x = 0}\\{{x^3} = 0}\\{{x^3} = 2 - x}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2}\\{x = 0}\\{x = 1}\end{array}} \right.\)
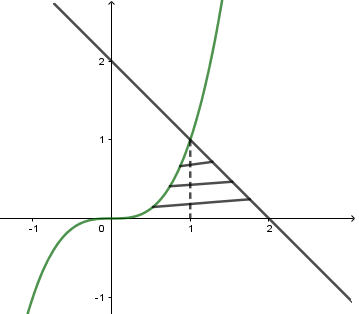
Nên diện tích hình phẳng cần tính là\[S = \mathop \smallint \limits_0^1 {x^3}dx + \mathop \smallint \limits_1^2 (2 - x)dx = \frac{1}{2} + \mathop \smallint \limits_0^1 {x^3}dx\]
Đáp án cần chọn là: C
Câu 11:
Cho hàm số y=f(x) liên tục trên R và thỏa mãn \[f\left( { - 1} \right) > 0 > f\left( 0 \right)\;\]. Gọi SS là diện tích hình phẳng giới hạn bởi các đường \[y = f(x),y = 0,x = 1\] và \[x = - 1\;\]. Mệnh đề nào sau đây là đúng
Đáp án cần chọn là: B
Câu 13:
Tính diện tích hình phẳng giới hạn bởi hai đường: \[y = \left| {{x^2} - 4x + 3} \right|\,\,\,;\,\,y = x + 3\]
Ta có\[\mid {x^2} - 4x + 3\mid = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 3}\end{array}} \right.\]
Ta có:
\[\left| {{x^2} - 4{\rm{x}} + 3} \right| = x + 3 \Leftrightarrow {{\rm{x}}^4} - 8{{\rm{x}}^3} + 22{{\rm{x}}^2} - 24{\rm{x}} + 9 = {x^2} + 6{\rm{x}} + 9\]
\[ \Leftrightarrow {x^4} - 8{x^3} + 21{x^2} - 30x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 5}\end{array}} \right.\]
Với\[0 \le x \le 5\]thì\[\left| {{x^2} - 4{\rm{x}} + 3} \right| \le x + 3\]
Có
\[\begin{array}{l}S = \int\limits_0^5 {\mid \mid x2 - 4x + 3\mid - x - 3\mid dx} \\ = \int\limits_0^1 {\left[ {x + 3 - (x2 - 4x + 3)} \right]} dx + \int\limits_1^3 {\left[ {x + 3 - ( - x2 + 4x - 3)} \right]} dx + \int\limits_3^5 {\left[ {x + 3 - (x2 - 4x + 3)} \right]} dx\end{array}\]
\( = \int\limits_0^1 {[ - x2 + 5x]dx + \int\limits_1^3 {[x2 - 3x + 6]dx + \int\limits_3^5 {[ - x2 + 5x]dx} } } \)
\( = \left( { - \frac{{{x^3}}}{3} + 5.\frac{{{x^2}}}{2}} \right)\left| {_0^1} \right. + \left( {\frac{{{x^3}}}{2} - 3.\frac{{{x^2}}}{2} + 6x} \right)\left| {_1^3} \right. + \left( { - \frac{{{x^3}}}{3} + 5.\frac{{{x^2}}}{2}} \right)\left| {_3^5} \right.\)
\( = - \frac{1}{3} + \frac{5}{4} + \frac{{27}}{2} - 3.\frac{9}{2} + 18 - \frac{1}{2} + \frac{3}{2} - 6 - \frac{{125}}{3} + \frac{{125}}{2} + \frac{{27}}{3} - \frac{{5.9}}{2} = \frac{{109}}{6}\)
Đáp án cần chọn là: B
Câu 14:
Diện tích hình phẳng giới hạn với đường cong \[y = 4 - \left| x \right|\] và trục hoành Ox là
Có\[4 - |x| = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 4}\\{x = - 4}\end{array}} \right.\]
Với\[ - 4 \le x \le 4\]thì\[4 - \left| x \right| \ge 0\]
Diện tích hình cần tìm là:
\(S = \int\limits_{ - 4}^4 {|4 - |x||dx = } \int\limits_{ - 4}^4 {(4 - |x|)dx = \int\limits_{ - 4}^0 {(4 + x)dx + \int\limits_0^4 {(4 - x)dx} } } \)
\( = 4x + \frac{{{x^2}}}{2}\left| {_{ - 4}^0} \right. + 4x - \frac{{{x^2}}}{2}\left| {_0^4} \right. = 0 + 16 - 8 + 16 - 8 = 16\)
Đáp án cần chọn là: B
Câu 15:
Gọi S là diện tích của Ban Công của một ngôi nhà có dạng như hình vẽ (S được giới hạn bởi parabol (P) và trục Ox). Giá trị của S là:
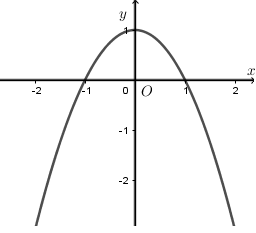
Gọi phương trình parabol:\[y = a{x^2} + bx + c(a \ne 0)\]
Parabol có đỉnh (0;1) nên\[c = 1\]và\[ - \frac{b}{{2a}} = 0\]hay b=0
Do đó\[y = a{x^2} + 1\]
Lại có các điểm (−1;0),(1;0) thuộc đồ thị hàm số nên\[a{.1^2} + 1 = 0 \Leftrightarrow a = - 1\]
Ta thấy, phương trình đường cong parabol trong hình là:\[y = - {x^2} + 1\]
\( \Rightarrow S = \int\limits_{ - 1}^1 {\mid 1 - x2\mid \mid dx = \left( {x - \frac{1}{3}{x^3}} \right)\left| {_{ - 1}^1} \right.} = \frac{4}{3}\)
Đáp án cần chọn là: C
Câu 16:
Người ta cần trồng hoa tại phần đắt nằm phía ngoài đường tròn tâm gốc tọa độ O , bán kính bằng \(\frac{1}{{\sqrt 2 }}\)và phía trong của Elip có độ dài trục lớn bằng \(2\sqrt 2 \)và độ dài trục nhỏ bằng 2 (như hình vẽ bên). Trong mỗi một đơn vị diện tích cần bón \(\frac{{100}}{{\left( {2\sqrt 2 - 1} \right)\pi }}kg\) phân hữu cơ. Hỏi cần sử dụng bao nhiêu kg phân hữu cơ để bón cho hoa?
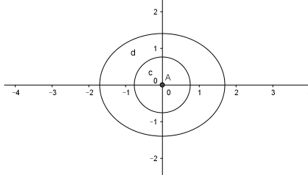
Phương trình elip:\[\frac{{{x^2}}}{{{{(\sqrt 2 )}^2}}} + \frac{{{y^2}}}{1} = 1\]
Ta có :\[y = \sqrt {1 - \frac{{{x^2}}}{2}} \] (nửa trên của elip)
Diện tích của elip là: \[S = 4\mathop \smallint \nolimits_0^{\sqrt 2 } \sqrt {1 - \frac{{{x^2}}}{2}} dx\]
Đặt\[x = \sqrt 2 \cos a \Rightarrow 1 - \frac{{{x^2}}}{2} = {\sin ^2}a\]
Suy ra:\[dx = - \sqrt 2 \sin ada\]
Đổi cận\[x = \sqrt 2 \Rightarrow a = 0,x = 0\]thì\[a = \frac{\pi }{2}\]
\({S_1} = \int\limits_{\frac{\pi }{2}}^0 { - \sqrt 2 si{n^2}ada = } \frac{{\sqrt 2 }}{2}\int\limits_{\frac{\pi }{2}}^0 {(cos2a - 1)da} \)
\( = \frac{{\sqrt 2 }}{2}\left( {\frac{1}{2}sin2a - a} \right)\left| {_0^{\frac{\pi }{2}}} \right. = \frac{{\sqrt 2 \pi }}{4}\)
\[ \Rightarrow S = 4{S_1} = \sqrt 2 \pi \]
Diện tích hình tròn là :\[S' = \pi {R^2} = \pi .\frac{1}{2} = \frac{1}{2}\pi \]
Diện tích trồng hoa: \[{S_b} = \pi \left( {\sqrt 2 - \frac{1}{2}} \right)\]
Số kg phân bón là :\[\frac{{100}}{{\left( {2\sqrt 2 - 1} \right)\pi }}.\left( {\sqrt 2 - \frac{1}{2}} \right)\pi = 50kg\]
Đáp án cần chọn là: C
Câu 17:
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi
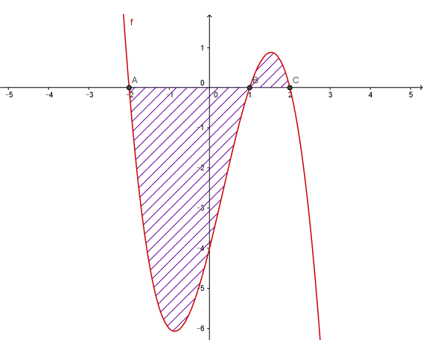
Nhận thấy phần đồ thị chia làm 2 phần, chú ý đến cận của từng phần.
Phần 1 có cận từ −2 đến 1 nhưng trong (−1;2), đồ thị hàm số nằm phía dưới trục hoành.
Phần 2 có cận từ 1 đến 2 và đồ thị hàm số nằm phía trên trục hoành.
Vậy\[S = \mathop \smallint \nolimits_{ - 2}^1 ( - f(x))dx + \mathop \smallint \nolimits_1^2 f(x)dx = \mathop \smallint \nolimits_1^{ - 2} f(x)dx + \mathop \smallint \nolimits_1^2 f(x)dx\]
Đáp án cần chọn là: B
Câu 18:
Vòm cửa lớn của một trung tâm văn hóa có hình parabol. Gắn parabol vào hệ trục Oxy thì nó có đỉnh (0;8) và cắt trục hoành tại 2 điểm phân biệt, trong đó có 1 điểm là (−4;0). Người ta dự định lắp vào cửa kính cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp vào.
+ Gọi phương trình parabol là: \[y = a{x^2} + bx + c\]
Nhận thấy với x=0 thì y=8 suy ra c=8.
Mặt khác (0;8) là đỉnh nên\[ - \frac{b}{{2a}} = 0 \Leftrightarrow b = 0\]
Điểm (−4;0) thuộc đồ thị hàm số nên phương trình y=0 có nghiệm
\[x = - 4 \Rightarrow a = - \frac{1}{2}\]
Vậy phương trình parabol:\[y = - \frac{{{x^2}}}{2} + 8\]
Bài toán quy về tính diện tích được tạo bởi parabol với trục Ox
Ta có:
\(S = \int\limits_{ - 4}^4 {\left| { - \frac{{{x^2}}}{2} + 8} \right|} dx = 2\int\limits_0^4 {\left( { - \frac{{{x^2}}}{2} + 8} \right)} dx\)
\( = 2.\left( { - \frac{{{x^3}}}{6} + 8x} \right)\left| {_0^4} \right. = \frac{{128}}{3}{m^2}\)
Đáp án cần chọn là: A
Câu 19:
Cho parabol \[\left( P \right):y = {x^2} + 1\]và đường thẳng \[(d):y = mx + 2\]. Biết rằng tồn tại m để diện tích hình phẳng giới hạn bới (P) và (d) đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó.
Phương trình hoành độ giao điểm dd và (P)
Có:\[{x^2} + 1 = mx + 2 \Leftrightarrow {x^2} - mx - 1 = 0(1) \Rightarrow {\rm{\Delta }} = {m^2} + 4 > 0\]
Phương trình trên luôn có 2 nghiệm phân biệt.
Vậy dd luôn cắt (P) tại hai điểm phân biệt A,B với mọi m.
Giả sử A,B lần lượt có hoành độ là a,b nên\[A\left( {a;ma + 2} \right)\]và\[B\left( {b;mb + 2} \right)(a < b)\]
Với x thuộc\[x \in \left( {a;b} \right)\]thì \[mx + 2 \ge {x^2} + 1\]
Do đó, diện tích hình phẳng giới hạn bởi d và (P)
\(\begin{array}{l}S = \int\limits_a^b {(mx + 2 - x2 - 1)dx} \\ = \int\limits_a^b {(mx - {x^2} + 1)dx = \left( {\frac{{m{x^2}}}{2} - \frac{{{x^3}}}{3} + x} \right)} \left| {_a^b} \right.\end{array}\)
\[ = \left( {b - a} \right)\left[ {\frac{m}{2}(a + b) + 1 - \frac{1}{3}({a^2} + {b^2} + ab)} \right]\]
\[ = (b - a)\left[ {\frac{m}{2}\left( {b + a} \right) + 1 - \frac{1}{3}{{\left( {a + b} \right)}^2} + \frac{1}{3}ab} \right]\]
\[ \Rightarrow {S^2} = {(b - a)^2}{\left[ {\frac{m}{2}(b + a) + 1 - \frac{1}{3}{{(a + b)}^2} + \frac{1}{3}ab} \right]^2}\]
\[ = \left[ {{{\left( {a + b} \right)}^2} - 4ab} \right]{\left[ {\frac{m}{2}\left( {b + a} \right) + 1 - \frac{1}{3}{{\left( {a + b} \right)}^2} + \frac{1}{3}ab} \right]^2}\]
Vì a,b là nghiệm của pt (1) nên a+b=m và ab=−1
Suy ra
\[{S^2} = \left( {{m^2} + 4} \right){\left( {\frac{{{m^2}}}{6} + \frac{2}{3}} \right)^2} \ge 4.\frac{4}{9} = \frac{{16}}{9} \Rightarrow S \ge \sqrt {\frac{{16}}{9}} = \frac{4}{3}\,khi\,m = 0\]
Đáp án cần chọn là: B
Câu 20:
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
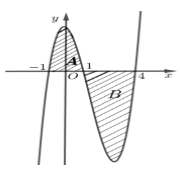
Diện tích hai phần A và B lần lượt là \(\frac{{16}}{3}\) và \(\frac{{63}}{4}\). Tính \[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx\]
Xét \[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx\] Đặt\[2x + 1 = t \Leftrightarrow 2dx = dt \Leftrightarrow dx = \frac{{dt}}{2}\]
Đổi cận:\(\left\{ {\begin{array}{*{20}{c}}{x = - 1 \Rightarrow t = - 1}\\{x = \frac{3}{2} \Rightarrow t = 4}\end{array}} \right.\)
Khi đó ta có\[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx = \frac{1}{2}\mathop \smallint \limits_{ - 1}^4 f\left( t \right)dt = \frac{1}{2}\mathop \smallint \limits_{ - 1}^4 f\left( x \right)dx\]
\[ = \frac{1}{2}\left( {\mathop \smallint \limits_{ - 1}^1 f\left( x \right)dx + \mathop \smallint \limits_1^4 f\left( x \right)dx} \right)\]
Từ hình vẽ ta có\[\mathop \smallint \limits_{ - 1}^1 f\left( x \right)dx = \frac{{16}}{3};\,\mathop \smallint \limits_1^4 f\left( x \right)dx = - \frac{{63}}{4}\]
Nên\[\mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx = \frac{1}{2}\left( {\mathop \smallint \limits_{ - 1}^1 f\left( x \right)dx + \mathop \smallint \limits_1^4 f\left( x \right)dx} \right) = \frac{1}{2}\left( {\frac{{16}}{3} - \frac{{63}}{4}} \right) = - \frac{{125}}{{24}}\]
Đáp án cần chọn là: C
Câu 21:
Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh 40(cm) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình \[4{x^2} = {y^4}\;\] và \[4{(|x| - 1)^3} = {y^2}\;\] để tạo hoa văn cho viên gạch. Diện tích phần được tô đậm gần nhất với giá trị nào dưới đây?
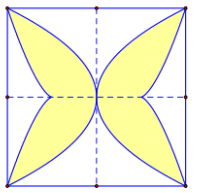
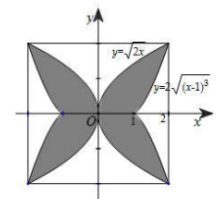
Gắn hệ trục tọa độ như hình vẽ.
Diện tích phần tô đậm là
\[S = 4\left[ {\mathop \smallint \limits_0^1 \left( {\sqrt {2x} - 0} \right)dx + \mathop \smallint \limits_1^2 \left( {\sqrt {2x} - 2\sqrt {{{\left( {x - 1} \right)}^3}} } \right)dx} \right] = \frac{{112}}{{15}}\,\,\left( {d{m^2}} \right) \approx 747\,\,\left( {c{m^2}} \right)\]
Đáp án cần chọn là: B
Câu 22:
Cho hàm số \[y = {x^4} - 3{x^2} + m\] có đồ thị là (Cm) (m là tham số thực). Giả sử (Cm) cắt trục Ox tại 4 điểm phân biệt. Gọi \[{S_1},{S_2}\;\] là diện tích của hai hình phẳng nằm dưới trục Ox và S3 là diện tích của hình phẳng nằm trên trục Ox được tạo bởi (Cm) với trục Ox. Biết rằng tồn tại duy nhất giá trị \[m = \frac{a}{b}\] (với \[a,b \in {\mathbb{N}^*}\;\] và tối giản) để \[{S_1} + {S_2} = {S_3}\]. Giá trị của 2a−b bằng:
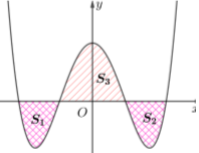
Xét phương trình hoành độ giao điểm:\[{x^4} - 3{x^2} + m = 0\,\,\,\left( 1 \right)\]
Đặt\[t = {x^2}\,\,\left( {t \ge 0} \right)\] khi đó phương trình (1) trở thành\[{t^2} - 3t + m = 0\,\,\,\left( 2 \right)\]
Vì đồ thị hàm số\[y = {x^4} - 3{x^2} + m\] cắt trục hoành tại 4 điểm phân biệt nên phương trình (1) có 4 nghiệm phân biệt, do đó phương trình (2) phải có 2 nghiệm dương phân biệt.
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta > 0}\\{S > 0}\\{P > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{9 - 4m > 0}\\{3 > 0(luon\,dung)}\\{m > 0}\end{array}} \right. \Leftrightarrow 0 < m < \frac{9}{4}\left( * \right)\)
Giả sử phương trình (2) có 2 nghiệm dương phân biệt\[0 < {t_1} < {t_2}\] áp dụng định lí Vi-ét ta có\(\left\{ {\begin{array}{*{20}{c}}{{t_1} + {t_2} = 3}\\{{t_1}{t_2} = m}\end{array}} \right.\) Khi đó phương trình (1) có 4 nghiệm phân biệt
\[ - \sqrt {{t_2}} < - \sqrt {{t_1}} < \sqrt {{t_1}} < \sqrt {{t_2}} \]
Do tính đối xứng qua trục tung của hàm đa thức bậc bốn trùng phương nên\[{S_1} = {S_2}\] do đó theo bài ra ta có \[{S_1} + {S_2} = {S_3} \Leftrightarrow 2{S_1} = {S_3}\]
Ta có:
\[{S_2} = \mathop \smallint \limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } \left| {f\left( x \right)} \right|dx = - \mathop \smallint \limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } f\left( x \right)dx\]
\[{S_3} = \mathop \smallint \limits_{ - \sqrt {{t_1}} }^{\sqrt {{t_1}} } \left| {f\left( x \right)} \right|dx = \mathop \smallint \limits_{ - \sqrt {{t_1}} }^{\sqrt {{t_1}} } f\left( x \right)dx = 2\mathop \smallint \limits_0^{\sqrt {{t_1}} } f\left( x \right)dx\] (do f(x) là hàm chẵn).
Ta có:
\(\begin{array}{l}2{S_2} = {S_3}\\ \Leftrightarrow - 2\int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {f(x)dx = 2\int\limits_0^{\sqrt {{t_1}} } {f(x)dx} } \\ \Leftrightarrow 2\left( {\int\limits_0^{\sqrt {{t_1}} } {f(x)dx} + \int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {f(x)dx} } \right) = 0\\ \Leftrightarrow 2\int\limits_0^{\sqrt {{t_2}} } {f(x)dx} = 0 \Leftrightarrow \int\limits_0^{\sqrt {{t_2}} } {f(x)dx = 0} \\ \Leftrightarrow \int\limits_0^{\sqrt {{t_2}} } {({x^4} - 3{x^2} + m)dx = 0} \\ \Leftrightarrow \left( {\frac{{{x^5}}}{5} - {x^3} + mx} \right)\left| {_0^{\sqrt {{t_2}} }} \right. = 0\\ \Leftrightarrow \frac{{{{\left( {\sqrt {{t_2}} } \right)}^5}}}{5} - {\left( {\sqrt {{t_2}} } \right)^3} + m\sqrt {{t_2}} = 0\\ \Leftrightarrow \sqrt {{t_2}} \left( {\frac{{{t^2}}}{5} - t + m} \right) = 0\\ \Leftrightarrow \frac{{{t_2}^2}}{5} - {t_2} + m = 0\,\,(Do\,\,{t_2} > 0)\,\\ \Leftrightarrow t_2^2 - 5{t_2} + 5m = 0( * )\end{array}\)
Mà \[{t_2}\] là nghiệm của phương trình\[{t^2} - 3t + m = 0\] nên\[t_2^2 - 3{t_2} + m = 0\] và\[{t_2} = \frac{{3 + \sqrt {9 - 4m} }}{2}\]
Do đó
\[\begin{array}{*{20}{l}}{\left( * \right) \Leftrightarrow t_2^2 - 3{t_2} + m - 2{t_2} + 4m = 0}\\{ \Leftrightarrow - 2{t_2} + 4m = 0 \Leftrightarrow {t_2} = 2m}\end{array}\]
\(\begin{array}{l} \Rightarrow \frac{{3 + \sqrt {9 - 4m} }}{2} = 2m\\ \Leftrightarrow 3 + \sqrt {9 - 4m} = 4m\\ \Leftrightarrow \sqrt {9 - 4m} = 4m - 3\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4m - 3 > 0}\\{9 - 4m = 16{m^2} - 24m + 9}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m > \frac{3}{4}}\\{16{m^2} - 20m = 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m > \frac{3}{4}}\\{\left[ {\begin{array}{*{20}{c}}{m = 0}\\{m = \frac{5}{4}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow m = \frac{5}{4}\left( {tm*} \right)\end{array}\)
Vậy \[a = 5,\,\,b = 4 \Rightarrow 2a - b = 10 - 4 = 6.\]
Đáp án cần chọn là: C
Câu 23:
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ).
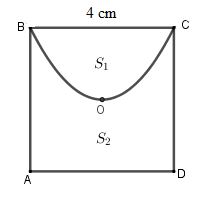
Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng:
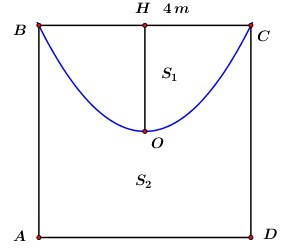
Gọi H là trung điểm của BC.
\[\begin{array}{*{20}{l}}{{S_1} = \frac{4}{3}Rh = \frac{4}{3}.HC.OH = \frac{4}{3}.2.2 = \frac{{16}}{3}\,{m^2}.}\\{{S_{ABCD}} = {4^2} = 16}\\{ \Rightarrow {S_2} = {S_{ABCD}} - {S_1} = 16 - \frac{{16}}{3} = \frac{{32}}{3}\,\,{m^2}.}\\{ \Rightarrow \frac{{{S_1}}}{{{S_2}}} = \frac{{16}}{3}:\frac{{32}}{3} = \frac{1}{2}.}\end{array}\]
Đáp án cần chọn là: A
Câu 24:
Cho hàm số f(x) có đồ thị trên đoạn \[\left[ { - 3;3} \right]\;\]là đường gấp khúc ABCD như hình vẽ.
Tính \[\mathop \smallint \limits_{ - 3}^3 f\left( x \right)dx\]
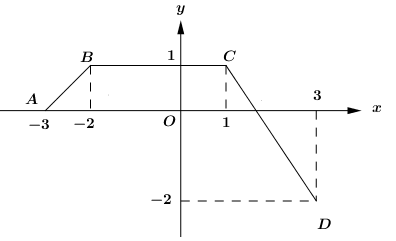
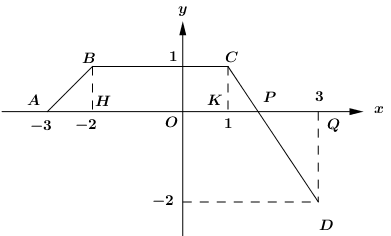
Ta có:
\[\begin{array}{*{20}{l}}{\mathop \smallint \limits_{ - 3}^3 f\left( x \right)dx = {S_{ABH}} + {S_{BCKH}} + {S_{CPK}} - {S_{DPQ}}}\\{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}.1.1 + 3.1 + \frac{1}{2}.1.\frac{2}{3} - \frac{1}{2}.\frac{4}{3}.2 = \frac{5}{2}}\end{array}\]
Đáp án cần chọn là: A
Câu 25:
Một khung cửa kính hình parabol với đỉnh M và cạnh đáy AB như minh họa ở hình bên. Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là 200.000 đồng /m2 và phần kính trắng còn lại là 150.000 đồng /m2/m2.Cho MN=AB=4m và MC=CD=DN. Hỏi số tiền để lắp kính cho khung cửa như trên gần nhất với số tiền nào dưới đây?
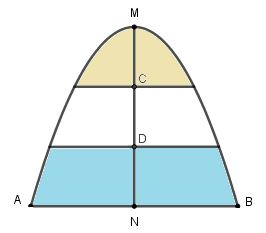
Coi N là gốc tọa độ thì ta có\[M\left( {0;4} \right);A\left( { - 2;0} \right);B\left( {2;0} \right)\]
Parabol có dạng\[y = - {x^2} + 4\]
Diện tích hình phẳng giới hạn bởi parobol và trục hoành là \[S = \mathop \smallint \limits_{ - 2}^2 \left| { - {x^2} + 4} \right|dx = \frac{{32}}{3}\]
Diện tích hình phẳng giới hạn bởi parobol là đường thẳng\[y = \frac{8}{3}\]là\[{S_1} = \mathop \smallint \limits_{ - \frac{{2\sqrt 3 }}{3}}^{\frac{{2\sqrt 3 }}{3}} \left| { - {x^2} + 4 - \frac{8}{3}} \right|dx\]
Diện tích hình phẳng giới hạn bởi parobol là đường thẳng\[y = \frac{4}{3}\]là\[{S_2} = \mathop \smallint \limits_{ - \frac{{2\sqrt 6 }}{3}}^{\frac{{2\sqrt 6 }}{3}} \left| { - {x^2} + 4 - \frac{4}{3}} \right|dx\]
Khi đó số tiền để lắp kính là\[T = 200.{S_1} + 150\left( {{S_2} - {S_1}} \right) + 200\left( {\frac{{32}}{3} - {S_2}} \right) = 1.946\]
Đáp án cần chọn là: C
Câu 26:
Cho hai hàm số \[f\left( x \right) = m{x^3} + n{x^2} + px - \frac{5}{2}\left( {m,n,p \in \mathbb{R}} \right)\]và\(g\left( x \right) = {x^2} + 3x - 1\) có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là −3;−1;1( tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số f(x)và g(x) bằng
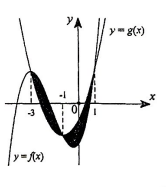
Đồ thị hàm số\[f\left( x \right) = m{x^3} + n{x^2} + px - \frac{5}{2}\]đi qua các điểm có tọa độ\[\left( {1;2} \right);\left( { - 1; - 2} \right);\left( { - 3;2} \right)\]nên ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{m + n + p - \frac{5}{2} = 2}\\{ - m + n - p - \frac{5}{2} = - 2}\\{ - 27m + 9n - 3p - \frac{5}{2} = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m = \frac{1}{2}}\\{n = \frac{5}{2}}\\{p = \frac{3}{2}}\end{array}} \right.\)
\[ \Rightarrow f\left( x \right) = \frac{1}{2}{x^3} + \frac{5}{2}{x^2} + \frac{3}{2}x - \frac{5}{2}.\]
Xét phương trình haonfh độ giao điểm\[f\left( x \right) = g\left( x \right) \Leftrightarrow f\left( x \right) - g\left( x \right) = 0\]
Dựa vào đồ thị ta thấy phương trình\[f\left( x \right) - g\left( x \right) = 0\]có 3 nghiệm là\(\left[ {\begin{array}{*{20}{c}}{{x_1} = - 3}\\{{x_2} = - 1}\\{{x_3} = 1}\end{array}} \right.\)
Do đó diện tích hình phẳng giới hạn bởi hai đồ thị hàm số\[f\left( x \right);g\left( x \right)\]bằng
\[S = \int\limits_{ - 3}^{ - 1} {[f(x) - g(x)]dx + \int\limits_{ - 1}^1 {[g(x) - f(x)]dx} } \]
\( = \int\limits_{ - 3}^{ - 1} {\left( {\frac{1}{2}{x^3} + \frac{5}{2}{x^2} + \frac{3}{2}x - \frac{5}{2} - {x^2} - 2x + 1} \right)dx + \int\limits_{ - 1}^1 {\left( {{x^2} + 2x - 1 - \frac{1}{2}{x^3} - \frac{5}{2}{x^2} - \frac{3}{2}x + \frac{5}{2}} \right)} } dx\)
\( = \int\limits_{ - 3}^{ - 1} {\left( {\frac{1}{2}{x^3} + \frac{3}{2}{x^2} - \frac{1}{2}x - \frac{3}{2}} \right)} dx + \int\limits_{ - 1}^1 {\left( { - \frac{1}{2}{x^3} - \frac{3}{2}{x^2} + \frac{1}{2}x + \frac{3}{2}} \right)} dx\)
\( = 2 + 2 = 4\)
Đáp án cần chọn là: C
Câu 27:
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \[f(x) = {x^3} + a{x^2} + bx + c\;\] với a,b,c là các số thực. Biết hàm số \[g(x) = f(x) + f\prime (x) + f\prime \prime (x)\;\] có hai giá trị cực trị là −3 và 6. Diện tích hình phẳng giới hạn bởi các đường \[y = \frac{{f(x)}}{{g(x) + 6}}\;v\`a \;y = 1\] bằng
* Xét phương trình hoành độ giao điểm:
\[\frac{{f\left( x \right)}}{{g\left( x \right) + 6}} = 1 \Leftrightarrow f\left( x \right) = g\left( x \right) + 6 \Leftrightarrow f\left( x \right) - g\left( x \right) - 6 = 0\]
(Chúng ta không cần lo điều kiện\[g\left( x \right) + 6 \ne 0\] bởi lẽ đồ thị hàm số \[y = \frac{{f\left( x \right)}}{{g\left( x \right) + 6}}\] khi tương giao với đường thẳng\[y = 1\] phải tạo nên một miền kín, và khi số nghiệm của phương trình\[f\left( x \right) = g\left( x \right) + 6\] nhiều hơn 2 thì ta mới phải chú ý xem xét lấy cận từ đâu đến đâu, và liệu rằng có phải từ\[{x_{\min }} \to {x_{\max }}\] chẳng may đồ thị tương giao bị gián đoạn trên đoạn\[\left[ {{x_{\min }};{x_{\max }}} \right]\] mà vẫn tạo miền kín. Trên thực tế, bài toán này phương trình\[f\left( x \right) = g\left( x \right) + 6\] chỉ có 2 nghiệm (vì là phương trình bậc hai), nên người giải toán không cần quan tâm đến việc gián đoạn hay không, vì việc tồn tại nghiệm hình và hàm số là thuộc phạm trù người ra đề).
Mà\[g\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right) \Rightarrow f\left( x \right) - g\left( x \right) = - f'\left( x \right) - f''\left( x \right)\]
⇒⇒ Phương trình hoành độ giao điểm trở thành:
\[ - f'\left( x \right) - f''\left( x \right) - 6 = 0 \Leftrightarrow f'\left( x \right) + f''\left( x \right) + 6 = 0\](1)
Mặt khác:\[g'\left( x \right) = f'\left( x \right) + f''\left( x \right) + f'''\left( x \right)\] và\[f'''\left( x \right) = 6\]
\[ \Rightarrow g'\left( x \right) = f'\left( x \right) + f''\left( x \right) + 6\]
Từ phương trình (1)\[ \Leftrightarrow g'\left( x \right) = 0\]
Theo giả thiết g(x) có 2 điểm cực trị\[{x_1},\,\,{x_2}\] sao cho\(\left\{ {\begin{array}{*{20}{c}}{g({x_1}) = - 3}\\{g({x_2}) = 6}\end{array}} \right. \Rightarrow g'\left( x \right) = 0\) có 2 nghiệm\[{x_1},\,\,{x_2}\]
Vậy phương trình hoành độ giao điểm có 2 nghiệm\[{x_1},\,\,{x_2}\]
\[ \Rightarrow {S_{\left( H \right)}} = \left| {\int\limits_{{x_1}}^{{x_2}} {\left( {\frac{{f(x)}}{{g(x) + 6}} - 1} \right)dx} } \right|\]
\[\begin{array}{l} = \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{f(x) - g(x) - 6}}{{g(x) + 6}}dx} } \right|\\ = \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{ - f\prime (x) - f\prime \prime (x) - 6}}{{g(x) + 6}}dx} } \right|\\ = \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{ - g\prime (x)}}{{g(x) + 6}}dx} } \right|\end{array}\]
\[ = \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{g\prime (x)}}{{g(x) + 6}}dx} } \right|\]
\[ = \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{d(g(x) + 6)}}{{g(x) + 6}}dx} } \right|\]
\[\begin{array}{l} = \mid ln|g(x) + 6||_{{x_1}}^{{x_2}}\mid \\ = |ln|g({x_2}) + 6| - ln|g({x_1}) + 6||\\ = |ln|6 + 6| - ln| - 3 + 6|| = ln12 - ln3 = 2ln2\end{array}\]
Đáp án cần chọn là: D