Đáp án cần chọn là: B

\[d:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 2}} = \frac{z}{3} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = - 1 - 2t}\\{z = 3t}\end{array}} \right.\]

\[ \Rightarrow M(1 + 2t; - 1 - 2t;3t)\]

\[M = d \cap \left( P \right) \Rightarrow 1 + 2t - 1 - 2t - 3t - 3 = 0 \Leftrightarrow - 3t - 3 = 0 \Leftrightarrow t = - 1 \Rightarrow M\left( { - 1;1; - 3} \right)\]

Đáp án cần chọn là: A

Đường thẳng d đi qua M(1;2;3) và có VTCP\[\overrightarrow {{u_d}} = \left( {3;3;1} \right)\]

Mặt phẳng (P)có VTPT\[\overrightarrow {{n_P}} = \left( {1; - 2;3} \right)\]

+)\[\overrightarrow {{u_d}} .\overrightarrow {{n_P}} = 3 - 6 + 3 = 0\](1)

+)\[1 - 2.2 + 3.3 - 1 \ne 0\] hay\[M \notin \left( P \right)\](2)

Từ (1) và (2), suy ra d song song với (P).

Đáp án cần chọn là: B

Giả sử M là giao điểm của (d) và (P). 

Lấy \[M \in (d) \Rightarrow M\left( {2t;1 - t;3 + t} \right)\]

Vì\[M \in (P) \Rightarrow 2t + 1 - t + 3 + t - 10 = 0 \Leftrightarrow 2t - 6 = 0 \Leftrightarrow t = 3\]

Suy ra ta có M(6;−2;6), suy ra d cắt (P) tại 1 điểm duy nhất. Do đó, loại đáp án A và B.

Mặt khác giả sử\[d \bot (P) \Rightarrow \frac{2}{1} = \frac{1}{1} = \frac{{ - 1}}{1}\](vô lý). Do đó loại C

Đáp án cần chọn là: D

Đáp án cần chọn là: C

Đáp án cần chọn là: A

Đáp án cần chọn là: D

Mặt phẳng (P) có VTPT\[\overrightarrow {{n_P}} = \left( {2; - 5;4} \right)\]

Gọi d là đường thẳng qua A và vuông góc với (P) nên có VTCP\[\overrightarrow {{u_d}} = \overrightarrow {{n_P}} = \left( {2; - 5;4} \right)\]

Do đó\[d:\frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 5}} = \frac{{z - 2}}{4}\]

Khi đó tọa độ hình chiếu H thỏa mãn hệ 

\(\left\{ {\begin{array}{*{20}{c}}{\frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 5}} = \frac{{z - 2}}{4}}\\{2x - 5y + 4z - 36 = 0}\end{array}} \right. \Rightarrow H(1; - 2;6)\)

Đáp án cần chọn là: C

Đáp án cần chọn là: D

Ta có:\(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{n_P}} = (1; - 1; - 1)}\\{\overrightarrow {{u_d}} = (2;1;3)}\end{array}} \right. \Rightarrow \left[ {\overrightarrow {{n_P}} ;\overrightarrow {{u_d}} } \right] = ( - 2; - 5;3)\)

Vì \[{\rm{\Delta }}\] vuông góc với d và song song với\[(P) \Rightarrow \overrightarrow {{u_{\rm{\Delta }}}} = \left[ {\overrightarrow {{n_P}} ,\overrightarrow {{u_d}} } \right] = \left( { - 2; - 5;3} \right)\]

Ta có:

\[(\Delta ):\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{u_\Delta }} = ( - 2; - 5;3)}\\{A(1;1; - 2) \in (\Delta )}\end{array}} \right. \Rightarrow \frac{{x - 1}}{{ - 2}} = \frac{{y - 1}}{{ - 5}} = \frac{{z + 2}}{3}\]

\[ \Leftrightarrow \frac{{x - 1}}{2} = \frac{{y - 1}}{5} = \frac{{z + 2}}{{ - 3}}\]Đáp án cần chọn là: C

Đáp án cần chọn là: A

Mặt phẳng (P) có VTPT\[\overrightarrow {{n_P}} = \left( {1;2; - 3} \right)\]; d có VTCP\[\overrightarrow {{u_d}} = \left( {1;1; - 1} \right)\]

Gọi \[A = d \cap \left( P \right)\] tọa độ điểm A thỏa mãn hệ

\(\left\{ {\begin{array}{*{20}{c}}{\frac{{x + 2}}{1} = \frac{{y - 2}}{1} = \frac{z}{{ - 1}}}\\{x + 2y - 3z + 4 = 0}\end{array}} \right. \Rightarrow A( - 3;1;1)\)

Do \[{\rm{\Delta }}\] nằm trong (P) và vuông góc với d nên có VTCP\[\overrightarrow {{u_{\rm{\Delta }}}} = \left[ {\overrightarrow {{n_P}} ,\overrightarrow {{u_d}} } \right] = \left( {1; - 2; - 1} \right)\]

Khi đó đường thẳng \[{\rm{\Delta }}\] được xác định là đi qua A(−3;1;1) và có VTCP \[\overrightarrow {{u_{\rm{\Delta }}}} = \left[ {\overrightarrow {{n_P}} ,\overrightarrow {{u_d}} } \right] = \left( {1; - 2; - 1} \right)\] nên có phương trình\[{\rm{\Delta }}:\frac{{x + 3}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 1}}{{ - 1}}\]

Đáp án cần chọn là: C

Xét đáp án A có

\[1 - 2.1 + 3.1 - 2 = 0 \Rightarrow A \in (P)\]

\[4 - 2.1 + 3.0 - 2 = 0 \Rightarrow B \in (P)\]

\[d(C,(P)) = \frac{{| - 1 - 8 - 3 - 2|}}{{\sqrt {1 + 4 + 9} }} = \sqrt {14} \]

Đáp án cần chọn là: A

Vì C,D cùng phía so với (P) và khoảng cách từ CC đến (P) bằng khoảng cách từ D đến (P) nên ta có (P)//CD

Ta có\[\overrightarrow {AB} = ( - 3; - 1;2);\overrightarrow {CD} = ( - 2;4;0) \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {CD} } \right] = ( - 8; - 4; - 14)\]

Vì\[(P)//CD\] và (P) đi qua hai điểm A,B nên ta có\[\overrightarrow {{n_P}} = \left[ {\overrightarrow {AB} ;\overrightarrow {CD} } \right]\] Chọn\[\overrightarrow {{n_P}} = (4;2;7)\]

\[ \Rightarrow (P):\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{n_P}} = (4;2;7)}\\{A(1;2;1) \in (P)}\end{array}} \right. \Rightarrow (P):4(x - 1) + 2(y - 2) + 7(z - 1) = 0\]

\[ \Leftrightarrow 4x + 2y + 7z - 15 = 0\]

Đáp án cần chọn là: C

Mặt phẳng (P) có VTPT\[\overrightarrow {{n_P}} = \left( {1;2;0} \right)\]

Gọi d là đường thẳng cần tìm. Ta có\[d \cap Ox = B\left( {b;0;0} \right)\]

Suy ra d có VTCP\[\overrightarrow {AB} = \left( {b + 1; - 3;4} \right)\]

Do d∥(P) nên

\[\overrightarrow {AB} \bot \overrightarrow {{n_P}} \Rightarrow \left( {b + 1} \right).1 + \left( { - 3} \right).2 + 4.0 = 0 \Leftrightarrow b = 5 \Rightarrow B\left( {5;0;0} \right).\]

Đường thẳng cần tìm đi qua hai điểm A,B nên có phương trình \(\left\{ {\begin{array}{*{20}{c}}{x = 5 + 6t}\\{y = - 3t}\\{z = 4t}\end{array}} \right.\)

Đáp án cần chọn là: A

Gọi I(a;b;c) là điểm thỏa mãn đẳng thức : \[2\overrightarrow {IA} + 3\overrightarrow {IB} = \vec 0\]

\[ \Rightarrow 2(2 - a; - 2 - b;4 - c) + 3( - 3 - a;3 - b; - 1 - c) = \overrightarrow 0 \]

\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{4 - 2a - 9 - 3a = 0}\\{ - 4 - 2b + 9 - 3b = 0}\\{8 - 2c - 3 - 3c = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 5a - 5 = 0}\\{ - 5b + 5 = 0}\\{ - 5c + 5 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = 1}\\{c = 1}\end{array}} \right. \Rightarrow I( - 1;1;1)\)

Ta có :

\[\begin{array}{*{20}{l}}{2M{A^2} + 3M{B^2} = 2{{\overrightarrow {MA} }^2} + 3{{\overrightarrow {MB} }^2}}\\{ = 2{{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)}^2} + 3{{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)}^2}}\\{ = 5M{I^2} + \left( {2I{A^2} + 3I{B^2}} \right) + \overrightarrow {MI} \left( {2\overrightarrow {IA} + 3\overrightarrow {IB} } \right)}\\{ = 5M{I^2} + \left( {2I{A^2} + 3I{B^2}} \right)}\end{array}\]

Do I, A, B cố định nên\[2I{A^2} + 3I{B^2} = const\]

\[ \Rightarrow {\left( {2M{A^2} + 3M{B^2}} \right)_{\min }} \Leftrightarrow 5M{I^2}_{\min }\]⇔ M là hình chiếu của I trên (P)

Gọi \[\left( {\rm{\Delta }} \right)\]là đường thẳng đi qua I vuông góc với (P) , ta có phương trình của

\(\left( \Delta \right):\left\{ {\begin{array}{*{20}{c}}{x = - 1 + 2t}\\{y = 1 - t}\\{z = 1 + 2t}\end{array}} \right.\)

M là hình chiếu của I lên (P) \[ \Rightarrow M \in \left( {\rm{\Delta }} \right) \Rightarrow M\left( { - 1 + 2t;1 - t;1 + 2t} \right)\]

Lại có\[M \in \left( P \right)\]

\[\begin{array}{*{20}{l}}{ \Rightarrow 2\left( { - 1 + 2t} \right) - \left( {1 - t} \right) + 2\left( {1 + 2t} \right) - 8 = 0}\\{ \Leftrightarrow - 2 + 4t - 1 + t + 2 + 4t - 8 = 0}\\{ \Leftrightarrow 9t - 9 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {1;0;3} \right)}\end{array}\]

Khi đó ta có

\[\begin{array}{*{20}{l}}{M{I^2} = 4 + 1 + 4 = 9;\;\;\;I{A^2} = 9 + 9 + 9 = 27;\;\;\;I{B^2} = 4 + 4 + 4 = 13}\\{ \Rightarrow {{\left( {2M{A^2} + 3M{B^2}} \right)}_{\min }} = 5.9 + 2.27 + 3.12 = 135}\end{array}\]

Đáp án cần chọn là: A

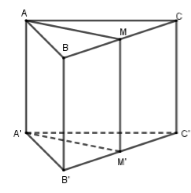
Phương trình \[BC \equiv Oz:\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = 0}\\{z = t}\end{array}} \right.\]

Mặt phẳng\[\left( {AMM'A'} \right)\] đi qua A′ và vuông góc với BC nên\[\left( {AMM'A'} \right)\] đi qua\[A'\left( {\sqrt 3 ; - 1;1} \right)\] và nhận\[\vec k = \left( {0;0;1} \right)\] làm VTPT hay

\[\left( {AMM'A'} \right):0\left( {x - \sqrt 3 } \right) + 0\left( {y + 1} \right) + 1\left( {z - 1} \right) = 0 \Leftrightarrow z = 1\]

\[M = BC \cap \left( {AMM'A'} \right) \Rightarrow t - 1 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {0;0;1} \right)\]

Mà \[AA' = 1,A'M = \sqrt {{{\left( {\sqrt 3 - 0} \right)}^2} + {{\left( { - 1 - 0} \right)}^2} + {{\left( {1 - 1} \right)}^2}} = 2\]

\[ \Rightarrow AM = \sqrt {A'{M^2} - A'{A^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \]

Tam giác ABC đều có độ dài đường cao\[AM = \frac{{BC\sqrt 3 }}{2} = \sqrt 3 \Rightarrow BC = 2\]

Gọi \[B\left( {0;0;m} \right),C\left( {0;0;n} \right)\] với\[n \ne 0\]  thì \[BC = 2 \Leftrightarrow \left| {m - n} \right| = 2\] và M(0;0;1) là trung điểm \[BC \Leftrightarrow \frac{{m + n}}{2} = 1 \Leftrightarrow m + n = 2\]

Khi đó \[m = 0,n = 2\]  vì\[n \ne 0\] hay C(0;0;2).

\[ \Rightarrow \overrightarrow {A'C} = \left( { - \sqrt 3 ;1;1} \right)\] hay\[2\overrightarrow {AC'} = \left( { - 2\sqrt 3 ;2;2} \right)\] là một VTCP của A′CA′C.

Suy ra \[a = - 2\sqrt 3 ,b = 2 \Rightarrow {a^2} + {b^2} = {\left( { - 2\sqrt 3 } \right)^2} + {2^2} = 16\]

Đáp án cần chọn là: B

Gọi\[N = d \cap {\rm{\Delta }}\]. Giả sử\[N\left( {2 - 2t;\,\,8 + t;\,\,t} \right) \Rightarrow \overrightarrow {MN} = \left( { - 2t;\,\,7 + t;\,\,t - 1} \right)\]

Đường thẳng\[{\rm{\Delta }}:\,\,\frac{{x - 2}}{{ - 2}} = \frac{{y - 8}}{1} = \frac{z}{1}\] có 1 VTCP là\[\overrightarrow {{u_{\rm{\Delta }}}} = \left( { - 2;1;1} \right)\]  đường thẳng d nhận\[\overrightarrow {MN} \] là 1 VTPT.

Do\[d \bot {\rm{\Delta }}\] nên\[\overrightarrow {MN} .\overrightarrow {{u_{\rm{\Delta }}}} = 0\]

\[\begin{array}{*{20}{l}}{ \Leftrightarrow - 2t.\left( { - 2} \right) + \left( {7 + t} \right).1 + \left( {t - 1} \right).1 = 0}\\{ \Leftrightarrow 6t + 6 = 0 \Leftrightarrow t = - 1}\\{ \Rightarrow \overrightarrow {MN} = \left( {2;6; - 2} \right)}\end{array}\]

⇒ Đường thẳng dd đi qua M(2;1;1) và có 1 VTCP\[\overrightarrow {{u_d}} = \frac{1}{2}\overrightarrow {MN} = \left( {1;3; - 1} \right)\] có phương trình là:\(\left\{ {\begin{array}{*{20}{c}}{x = 2 + t'}\\{y = 1 + 3t'}\\{z = 1 - t'}\end{array}} \right.\)

Khi đó, giao điểm của d và mặt phẳng (Oyz) ứng với t′ thỏa mãn

\[x = 2 + t' = 0 \Leftrightarrow t' = - 2\]

⇒ Tọa độ giao điểm của d và mặt phẳng (Oyz) là: (0;−5;3).

Đáp án cần chọn là: B

Gọi\[M = d \cap {{\rm{\Delta }}_1} \Rightarrow M\left( {1 + {t_1};\,\, - 2 + 4{t_1};\,\,2 + 3{t_1}} \right)\]

\[N = d \cap {{\rm{\Delta }}_2} \Rightarrow N\left( { - 4 + 5{t_2};\,\, - 7 + 9{t_2};\,\,{t_2}} \right)\]

\[ \Rightarrow \overrightarrow {MN} = \left( {5{t_2} - {t_1} - 5;\,\,9{t_2} - 4{t_1} - 5;\,\,{t_2} - 3{t_1} - 2} \right)\]

Vì\[d \bot \left( P \right):\,\,4y - z + 3 = 0\] có 1 VTPT là\[\vec n\left( {0;4; - 1} \right)\] nên\[\overrightarrow {MN} \] và\[\vec n\] là 2 vectơ cùng phương.

\[ \Rightarrow \overrightarrow {MN} = k\vec n\,\,\left( {k \ne 0} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5{t_2} - {t_1} - 5 = 0}\\{9{t_2} - 4{t_1} - 5 = 4k}\\{{t_2} - 3{t_1} - 2 = - k}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t_1} = 5{t_2} - 5}\\{9{t_2} - 4{t_1} - 5 = 4k}\\{4{t_2} - 12{t_1} - 8 = - 4k}\end{array}} \right.\]

\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t_1} = 5{t_2} - 5}\\{13{t_{_2}} - 16{t_1} - 13 = 0}\\{{t_2} - 3{t_1} - 2 = - k}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t_1} = 5{t_2} - 5}\\{13{t_2} - 16(5{t_2} - 5) - 13 = 0}\\{{t_2} - 3{t_1} - 2 = - k}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t_1} = 5{t_2} - 5}\\{ - 67{t_2} + 67 = 0}\\{{t_2} - 3{t_1} - 2 = - k}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t_2} = 1}\\{{t_1} = 0}\\{k = 1}\end{array}} \right.\end{array}\)

\[ \Rightarrow M\left( {1;\,\, - 2;\,\,2} \right),\,\,N\left( {1;\,\,2;\,\,1} \right) \Rightarrow \overrightarrow {MN} = \left( {0;4; - 1} \right)\]

Vậy phương trình đường thẳng d đi qua M và có 1 VTCP\[\overrightarrow {MN} \left( {0;4; - 1} \right)\] là:

\(\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = - 2 + 4t}\\{z = 2 - t}\end{array}} \right.\)

Đáp án cần chọn là: A

Vì \[M \in d:\,\,\frac{x}{{ - 2}} = \frac{{y - 1}}{1} = \frac{z}{1} \Rightarrow \] Gọi\[M\left( { - 2t;\,\,1 + t;\,\,t} \right)\]

Ta có:\[OM = \sqrt {{{\left( { - 2t} \right)}^2} + {{\left( {1 + t} \right)}^2} + {t^2}} = \sqrt {6{t^2} + 2t + 1} \]

\[d\left( {M;\left( P \right)} \right) = \frac{{\left| {2\left( { - 2t} \right) - \left( {1 + t} \right) + 2t - 2} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} }} = \frac{{\left| { - 3t - 3} \right|}}{3} = \left| {t + 1} \right|\]

Theo bài ra ta có: M cách đều gốc tọa độ O và mặt phẳng (P)\[ \Leftrightarrow \sqrt {6{t^2} + 2t + 1} = \left| {t + 1} \right|\]

\[\begin{array}{*{20}{l}}{ \Leftrightarrow 6{t^2} + 2t + 1 = {t^2} + 2t + 1}\\{ \Leftrightarrow 5{t^2} = 0 \Leftrightarrow t = 0}\end{array}\]

\[ \Rightarrow M\left( {0;1;0} \right)\]

Vậy có 1 điểm M  thỏa mãn yêu cầu bài toán là M(0;1;0).

Đáp án cần chọn là: D

Ta có\[A\left( {4; - 3;5} \right),B\left( {2; - 5;1} \right)\]nên trung điểm của AB là I(3;−4;3).

Đường thẳng\[\left( d \right):\frac{{x + 1}}{3} = \frac{{y - 5}}{{ - 2}} = \frac{{z + 9}}{{13}}\]có 1 VTCP là\[\overrightarrow {{u_d}} = \left( {3; - 2;13} \right)\]

Mặt phẳng (P) vuông góc với d  nên mặt phẳng (P) có 1 VTPT\[\overrightarrow {{n_P}} = \overrightarrow {{u_d}} = \left( {3; - 2;13} \right)\]

Mặt phẳng (P) có vectơ pháp tuyến là\[\vec n = \left( {3; - 2;13} \right)\]và đi qua I(3;−4;3) có phương trình là

\[3\left( {x - 3} \right) - 2\left( {y + 4} \right) + 13\left( {z - 3} \right) = 0 \Leftrightarrow 3x - 2y + 13z - 56 = 0\]

Đáp án cần chọn là: A

Đáp án cần chọn là: D

Bước 1: Viết phương trình mặt phẳng (P) là mặt phẳng đi qua M và vuông góc với \[{\rm{\Delta }}\].

Ta có: \[{\rm{\Delta }}:\,\,\,\frac{x}{1} = \frac{{y + 2}}{2} = \frac{{z - 1}}{1}\] và M(2;0;1)

Gọi (P) là mặt phẳng đi qua M và vuông góc với\[{\rm{\Delta }} \Rightarrow \overrightarrow {{n_P}} = \overrightarrow {{u_{\rm{\Delta }}}} = \left( {1;\,\,2;\,\,1} \right).\]

\[ \Rightarrow \left( P \right):\,\,\,x - 2 + 2y + z - 1 = 0 \Leftrightarrow x + 2y + z - 3 = 0.\]

Bước 2:  Tìm tọa độ điểm\[H = \left( P \right) \cap {\rm{\Delta }}\]  khi đó H là trung điểm của MM′, từ đó tìm tọa độ điểm M′.

Gọi H là giao điểm của (P) và \[{\rm{\Delta }}\]

⇒ Toạ độ của H là nghiệm của hệ phương trình:

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{\frac{x}{1} = \frac{{y + 2}}{2} = \frac{{z - 1}}{1}}\\{x + 2y + z - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = - 2 + 2t}\\{z = 1 + t}\\{x + 2y + z - 3 = 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = - 2 + 2t}\\{z = 1 + t}\\{t - 4 + 4t + 1 + t - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = - 2 + 2t}\\{z = 1 + t}\\{t = 1}\end{array}} \right.\end{array}\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 0}\\{z = 2}\end{array}} \right. \Rightarrow H(1;0;2)\)

Ta có: M′ là điểm đối xứng của M qua \[{\rm{\Delta }}\] ⇒H là trung điểm của MM′ ⇒M′(0;0;3)

Bước 3: Khoảng cách từ \[M\left( {{x_0};{y_0}} \right)\]đến mặt phẳng (P)

Ta có: (Oxy):z=0.

\[ \Rightarrow d\left( {M;\,\,\left( {Oxy} \right)} \right) = \frac{{\left| 3 \right|}}{1} = 3.\]

Bước 1: Gọi\[A = d \cap Oxy \Rightarrow \] Tìm tọa độ điểm AA.

Mặt phẳng Oxy có phương trình z=0.

Gọi \[A = d \cap Oxy \Rightarrow \] Tọa độ của A là nghiệm của hệ phương trình

\(\left\{ {\begin{array}{*{20}{c}}{x = 2 - 2t}\\{y = 0}\\{z = t}\\{z = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2}\\{y = 0}\\{z = 0}\end{array}} \right. \Rightarrow A(2;0;0)\)

Bước 2: Lấy điểm B bất kì thuộc d. Gọi B′ là điểm đối xứng với B qua Oxy⇒ Tìm tọa độ điểm B′.

Lấy \[B\left( {0;0;1} \right) \in d\] Gọi B′ là điểm đối xứng với B qua \[Oxy \Rightarrow B'\left( {0;0; - 1} \right)\].

Bước 3: d′ là đường thẳng đối xứng với d qua mặt phẳng Oxy ⇒d′ đi qua A,B′. Viết phương trình đường thẳng d′.

d′ là đường thẳng đối xứng với d qua mặt phẳng Oxy ⇒d′ đi qua A,B′.

⇒d′ nhận\[\overrightarrow {AB'} = \left( { - 2;0; - 1} \right)//\left( {2;0;1} \right)\]  là 1 VTCP ⇒\(d':\left\{ {\begin{array}{*{20}{c}}{x = 2 + 2t}\\{y = 0}\\{z = t}\end{array}} \right.\)

\( \Rightarrow a = 2,b = 2,c = 0\)

\( \Rightarrow a + b + c = 2 + 2 + 0 = 4\)Câu 28. Trong không gian Oxyz, gọi d′ là hình chiếu vuông góc của đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = t}\\{z = t}\end{array}} \right.\) trên mặt phẳng (Oxy). Phương trình tham số của đường thẳng d′ là

A.\(\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 0}\\{z = t}\end{array}} \right.\)

B. \(\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = t}\\{z = 0}\end{array}} \right.\)

C. \(\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = t}\\{z = t}\end{array}} \right.\)

D. \(\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = 0}\\{z = t}\end{array}} \right.\)

Bước 1:

Đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = t}\\{z = t}\end{array}} \right.\) đi qua hai điểm O(0;0;0) và A(1;1;1).

Bước 2:

Hình chiếu của điểm O,A trên (Oxy) lần lượt là O(0;0;0) và A′(1;1;0).

Bước 3:

Khi đó hình chiếu của d là đường thẳng d′d′ đi qua O,A′, nhận \[\overrightarrow {OA'} = \left( {1;1;0} \right)\]là 1 VTCP nên có phương trình tham số là \(\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = t}\\{z = 0}\end{array}} \right.\)

Đáp án cần chọn là: B

Bước 1: Viết phương trình đường thẳng \[{\rm{\Delta }}\] đi qua A và vuông góc với (P).

Gọi \[{\rm{\Delta }}\] là đường thẳng đi qua A và vuông góc với (P), phương trình đường thẳng \[{\rm{\Delta }}\] là:

\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = 1 - 2t}\\{z = - 2 - t}\end{array}} \right.\left( \Delta \right)\)

Bước 2: Tìm\[H = {\rm{\Delta }} \cap \left( P \right)\]

Vì H là hình chiếu vuông góc của A trên (P) nên\[H = {\rm{\Delta }} \cap \left( P \right)\] ⇒ Tọa độ điểm H là nghiệm của hệ phương trình

\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = 1 - 2t}\\\begin{array}{l}z = - 2 - t\\2x - 2y - z + 7 = 0\end{array}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = 1 - 2t}\\{z = - 2 - t}\\{2 + 4t - 2 + 4t + 2 + t + 7 = 0}\end{array}} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = 1 - 2t}\\{z = - 2 - t}\\{9t + 9 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{t = - 1}\\{x = - 1}\\{y = 3}\\{z = - 1}\end{array}} \right. \Rightarrow H( - 1;3; - 1)\)

Bước 3: Tìm a,b,c và tính tổng.

\[ \Rightarrow a = - 1,\,\,b = 3,\,\,c = - 1\]

Vậy\[a + b + c = - 1 + 3 - 1 = 1\]

A′(a;b;c) là điểm đối xứng với điểm A(−1;0;3) qua mặt phẳng\[\left( P \right):x + 3y - 2z - 7 = 0\]

Khi đó, ta có:\(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{\rm{AA}}'} //\overrightarrow {{n_P}} }\\{I \in (P)}\end{array}} \right.\) với I là trung điểm của AA’

\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{a + 1}}{1} = \frac{{b - 0}}{3} = \frac{{c - 3}}{{ - 2}}}\\{\left( {\frac{{a - 1}}{2}} \right) + 3.\frac{b}{2} - 2.\frac{{c + 3}}{2} - 7 = 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{a + 1}}{1} = \frac{b}{3} = \frac{{c - 3}}{{ - 2}}}\\{a + 3b - 2c = 21}\end{array}} \right.\end{array}\)

\[ \Rightarrow \frac{{a + 1}}{1} = \frac{b}{3} = \frac{{c - 3}}{{ - 2}} = \frac{{a + 1 + 3b - 2c + 6}}{{1 + 9 + 4}} = \frac{{21 + 1 + 6}}{{14}} = 2\]

\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = 6}\\{c = - 1}\end{array}} \right. \Rightarrow A'\left( {1;6; - 1} \right)\)

Vậy\[a + b + c = 1 + 6 + ( - 1) = 6\]