Bài tập mạch xoay chiều chứa RLC
-
257 lượt thi
-
21 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Một mạch điện xoay chiều có u là điện áp tức thời ở hai đầu đoạn mạch và i là cường độ tức thời qua mạch. Chọn phát biểu đúng:
Trả lời:
A - đúng
B, C, D - sai vì tùy loại mạch mà u và i có độ lệch pha khác nhau
Đáp án cần chọn là: A
Câu 2:
Đặt vào hai đầu đoạn mạch chỉ có điện trở thuần R một điện áp xoay chiều có biểu thức u = U0cos(ωt) V thì cường độ dòng điện chạy qua điện trở có biểu thức \[i = I\sqrt 2 \cos \left( {\omega t + {\varphi _i}} \right)A\], trong đó I và φi được xác định bởi các hệ thức tương ứng là
Trả lời:
Ta có:
+ Cường độ dòng điện hiệu dụng trong mạch chỉ có R:
\[I = \frac{U}{R} = \frac{{{U_0}}}{{\sqrt 2 R}}\]
+ Cường độ dòng điện và hiệu điện thế trong mạch chỉ có R dao động cùng pha với nhau
=>φi = φu = 0
Đáp án cần chọn là: D
Câu 3:
Đoạn mạch điện xoay chiều gồm hai điện trở thuần R1 = 20 Ω và R2 = 40 Ω mắc nối tiếp với nhau. Đặt vào giữa hai đầu đoạn mạch một điện áp xoay chiều có biểu thức \[u = 120\sqrt 2 \cos 100\pi t\,V\]. Kết luận nào sau đây là không đúng ?
Trả lời:
Ta có tổng trở của mạch: R = R1 + R2 = 60Ω
Cường độ dòng điện hiệu dụng trong mạch:
\[I = \frac{U}{R} = \frac{{120}}{{60}} = 2A\]
Cường độ dòng điện cực đại qua R1 và R2 là như nhau và bằng:
\[{I_{01}} = {I_{02}} = {I_0} = \frac{{{U_0}}}{R} = \frac{{120\sqrt 2 }}{{60}} = 2\sqrt 2 A\]
Cường độ dòng điện và hiệu điện thế trong mạch dao động cùng pha nhau
=>Biểu thức cường độ dòng điện trong mạch:
\[i = 2\sqrt 2 \cos 100\pi t\,\]
Đáp án cần chọn là: D
Câu 4:
Mắc điện trở R = 55Ω vào mạng điện xoay chiều có điện áp \[u = 110\cos \left( {100\pi t + \frac{\pi }{2}} \right)\left( V \right)\]. Nhiệt lượng toả ra ở R trong 10 phút là:
Trả lời:
Ta có, cường độ dòng điện cực đại trong mạch:
\[{I_0} = \frac{{{U_0}}}{R} = \frac{{110}}{{55}} = 2A\]
Nhiệt lượng tỏa ra trên R trong 10 phút là:
\[Q = {I^2}Rt = \frac{{I_0^2Rt}}{2}\]
\[ \to Q = \frac{{{2^2}.55.10.60}}{2} = 66000J = 66kJ\]
Đáp án cần chọn là: B
Câu 5:
Một cuộn dây thuần cảm có độ tự cảm L được mắc vào điện áp xoay chiều u có tần số f. Chọn phát biểu đúng:
Trả lời:
A- sai vì: Cường độ dòng điện trong mạch chỉ có L trễ pha hơn điện áp u
B- đúng
C- sai vì:
\[I = \frac{U}{{{Z_L}}} = \frac{U}{{\omega L}} = \frac{U}{{2\pi fL}}\]
=>cường độ dòng điện tỉ lệ nghịch với L và f
D- sai vì cường độ dòng điện biến thiên điều hòa với tần số f
Đáp án cần chọn là: B
Câu 6:
Tác dụng của cuộn cảm đối với dòng điện xoay chiều là:
Trả lời:
Ta có, cảm kháng:
ZL = 2πfL
=>cảm kháng lớn nếu tần số dòng điện lớn
Đáp án cần chọn là: C
Câu 7:
Đoạn mạch điện xoay chiều chỉ có cuộn cảm có hệ số tự cảm L. Điện áp tức thời và cường độ dòng điện tức thời của mạch là u và i. Điện áp hiệu dụng và cường độ hiệu dụng là U, I. Biểu thức nào sau đây là đúng?
Trả lời:
Mạch chỉ có cuộn cảm nên điện áp nhanh pha hơn dòng điện góc \[\frac{\pi }{2}\]
Khi đó ta có
\[\left\{ {\begin{array}{*{20}{c}}{u = {U_C}\cos \left( {\omega t + {\varphi _u}} \right) = U\sqrt 2 \cos \left( {\omega t + {\varphi _u}} \right)}\\{i = {I_0}\cos \left( {\omega t + {\varphi _u} - \frac{\pi }{2}} \right) = I\sqrt 2 \sin \left( {\omega t + {\varphi _u}} \right)}\end{array}} \right.\]
\[ \to {\left( {\frac{u}{{U\sqrt 2 }}} \right)^2} + {\left( {\frac{i}{{I\sqrt 2 }}} \right)^2} = 1\]
\[ \leftrightarrow {\left( {\frac{u}{U}} \right)^2} + {\left( {\frac{i}{I}} \right)^2} = 2\]
Đáp án cần chọn là: B
Câu 8:
Mạch điện xoay chiều chỉ có tụ điện với điện dung C. Đặt vào hai đầu tụ điện một điện áp u = U0cos(ωt + φ) V. Cường độ dòng điện hiệu dụng của mạch được cho bởi công thức:
Trả lời:
Ta có: Cường độ dòng điện hiệu dụng trong mạch:
\[I = \frac{U}{{{Z_C}}} = \frac{U}{{\frac{1}{{\omega C}}}}\]
\[ \to I = U\omega C = \frac{{{U_0}}}{{\sqrt 2 }}\omega C\]
Đáp án cần chọn là: B
Câu 9:
Cho đoạn mạch điện xoay chiều chỉ có tụ điện với điện dung \[C = \frac{{{{10}^{ - 4}}}}{\pi }\left( F \right)\]. Đặt điện áp xoay chiều có tần số 50Hz vào hai đầu đoạn mạch. Tại thời điểm mà điện áp hai đầu mạch có giá trị \[100\sqrt {10} V\]thì cường độ dòng điện trong mạch là \[\sqrt 2 A\]. Điện áp hiệu dụng hai đầu tụ điện có giá trị là:
Trả lời:
Dung kháng của mạch là :
\[{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi .50.\frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \]
Áp dụng hệ thức liên hệ ta được:
\[{\left( {\frac{{{u_C}}}{{{U_{0C}}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1\]
\[ \leftrightarrow {\left( {\frac{{100\sqrt {10} }}{{100{I_0}}}} \right)^2} + {\left( {\frac{{\sqrt 2 }}{{{I_0}}}} \right)^2} = 1\]
\[ \leftrightarrow \frac{{10}}{{I_0^2}} + \frac{2}{{I_0^2}} = 1\]
\[ \to {I_0} = 2\sqrt 3 A\]
\[ \to {U_{0C}} = {I_0}{Z_C} = 200\sqrt 3 V\]
\[ \to {U_C} = \frac{{{U_{0C}}}}{{\sqrt 2 }} = \frac{{200\sqrt 3 }}{{\sqrt 2 }}\]
\[ \to {U_C} = 100\sqrt 6 V\]
Đáp án cần chọn là: B
Câu 10:
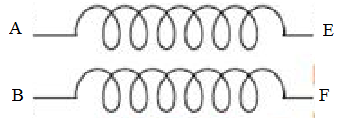
Một học sinh mắc mạch điện như hình vẽ. Đặt vào A và B điện áp xoay chiều
\[u = U\sqrt 2 \cos \left( {100\pi t} \right)\] (U không đổi). Khi nối E, F với một ampe kế thì số chỉ của ampe kế là 3,8A. Khi nối E, F với một vôn kế thì số chỉ của vôn kế là 11,95V. Coi như hai cuộn dây thuần cảm và có hệ số tự cảm bằng nhau. Độ tự cảm cảu mỗi cuộn dây gần nhấu với giá trị nào sau đây?
Trả lời:
Khi mắc ampe kế vào E,F ta đo được cường độ dòng điện chạy trong mạch :
\[I = \frac{U}{{2{Z_L}}} \Rightarrow {Z_L} = \frac{U}{{2I}}\]
Khi mắc Vôn kế vào E, F thì ta đo được hiệu điện thế giữa hai điểm E, F tức là A, B (vì vôn kế lý tưởng và mạch thuần cảm). Vậy là U = 11,95V.
Lại có :
\[I = \frac{U}{{2{Z_L}}} \Rightarrow {Z_L} = \frac{U}{{2I}} = \frac{{11,95}}{{2.3,8}} = 1,572\Omega \]
Từ công thức tính cảm kháng ta có :
\[L = \frac{{{Z_L}}}{\omega } = \frac{{1,572}}{{100\pi }} = {5.10^{ - 3}}H = 5mH\]
Đáp án cần chọn là: A
Câu 11:
Một mạch điện xoay chiều nối tiếp có \[R = 60\Omega ;L = \frac{{0,2}}{\pi }H;C = \frac{{{{10}^{ - 4}}}}{\pi }F\] mắc vào mạng điện xoay chiều có chu kì 0,02s. Tổng trở của đoạn mạch là:
Trả lời:
Ta có:
\[\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,02}} = 100\pi \left( {rad/s} \right)\]
\[R = 60\Omega \]
\[{Z_L} = \omega L = 100\pi \frac{{0,2}}{\pi } = 20\Omega \]
\[{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi \frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \]
Tổng trở của mạch:
\[Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \]
\[Z = \sqrt {{{60}^2} + {{\left( {20 - 100} \right)}^2}} = 100\Omega \]
Đáp án cần chọn là: CCâu 12. Mạch nối tiếp gồm ampe kế, C = 63, 6μF,L = 0,318H rồi mắc vào mạng điện xoay chiều (220V – 50Hz). Số chỉ ampe kế là:
A. 2,2 A
B. 4,4 A
C. 1,1 A
D. 8,8 A
Trả lời:
Ta có:
+ Hiệu điện thế hiệu dụng: U = 220V
+ Cảm kháng:
ZL = ωL = 2πfL = 2π.50.0,318 = 100Ω
+ Dung kháng:
\[{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}}\]
\[{Z_C} = \frac{1}{{2\pi .50.63,{{6.10}^{ - 6}}}} = 50\Omega \]
+ Tổng trở của mạch: Z = |ZL – ZCC| = 50Ω
Số chỉ ampe kế chính là cường độ dòng điện hiệu dụng:
\[I = \frac{U}{Z} = \frac{{220}}{{50}} = 4,4\left( A \right)\]
Đáp án cần chọn là: B
Câu 12:
Đoạn mạch RLC nối tiếp. Biết điện áp tức thời ở hai đầu đoạn mạch sớm pha hơn cường độ dòng điện tức thời i chạy qua mạch 450. Chọn kết luận đúng:
Trả lời:
Ta có :
+ u nhanh pha hơn i một góc 450
+ độ lệch pha giữa u và i được xác định bởi biểu thức :
\[\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\]
\[ \to \tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \tan \frac{\pi }{4}\]
\[ \to {Z_L} - {Z_C} = R\]
Đáp án cần chọn là: A
Câu 13:
Mạch điện xoay chiều RLC nối tiếp. Biết điện áp tức thời giữa hai đầu đoạn mạch chậm pha hơn cường độ dòng điện tức thời là: 600 và \[R = 10\sqrt 3 \Omega ;{Z_L} = 50\Omega \]. Dung kháng của tụ điện có giá trị là
Trả lời:
Ta có, điện áp tức thời giữa hai đầu đoạn mạch chậm pha hơn cường độ dòng điện tức thời góc 600
\[ \to \varphi = - \frac{\pi }{3}\]
Mặt khác, ta có:
\[\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \tan \left( { - \frac{\pi }{3}} \right)\]
\[ \to {Z_L} - {Z_C} = - \sqrt 3 R\]
\[ \to {Z_C} = {Z_{:L}} + \sqrt 3 R\]
\[ \to {Z_C} = 50 + \sqrt 3 .10\sqrt 3 \]
\[ \to {Z_C} = 80\Omega \]
Đáp án cần chọn là: D
Câu 14:
Điện áp của mạch điện xoay chiều là \[u = 100\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{2}} \right)V\] và cường độ dòng điện qua mạch là \[i = 5\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{3}} \right)A\]. Trong mạch điện có thể có:
Trả lời:
Ta có:
\[u = 100\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{2}} \right)V\] và \[i = 5\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{3}} \right)A\]
=>Độ lệch pha giữa u và i:
\[\varphi = \frac{\pi }{2} - \frac{\pi }{3} = \frac{\pi }{6} >0\]
Mặt khác, ta có:
\[\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\]
=>Mạch có thể chứa R, L, C trong đó ZL >ZC hoặc mạch chỉ chứa R và L
Đáp án cần chọn là: D
Câu 15:
Trong đoạn mạch điện xoay chiều RLC nối tiếp, nếu điện áp hiệu dụng giữa hai bản tu gấp hai lần điện áp điện áp hiệu dụng giữa hai đầu cuộn dây thuần cảm thì điện áp giữa hai đầu đoạn mạch sẽ
Trả lời:
Ta có giản đồ vecto trong trường hợp: UC = 2.UL:
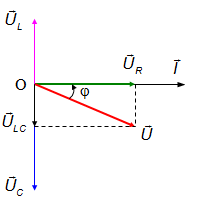
Vậy u trễ pha với i.
Đáp án cần chọn là: A
Câu 16:
Đặt điện áp u = U0cos(ωt) vào hai đầu cuộn cảm thuần có độ tự cảm L thì cường độ dòng điện qua cuộn cảm thuần là:
Trả lời:
Ta có:
+ uL nhanh pha hơn i một góc \[\frac{\pi }{2}\]
+ Cường độ dòng điện cực đại:
\[{I_0} = \frac{{{U_0}}}{{{Z_L}}} = \frac{{{U_0}}}{{\omega L}}\]
=>Biểu thức cường độ dòng điện qua cuộn cảm thuần là:
\[i = \frac{{{U_0}}}{{\omega L}}\cos \left( {\omega t - \frac{\pi }{2}} \right)\]
Đáp án cần chọn là: C
Câu 17:
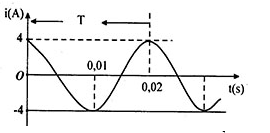
Đồ thị cường độ dòng điện như hình vẽ
Cường độ dòng điện tức thời có biểu thức
Trả lời:
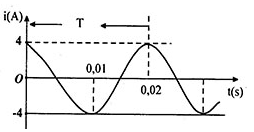
Từ đồ thị ta có:
+ Chu kì:
\[T = 0,02s\]
\[ \to \omega = \frac{{2\pi }}{T} = 100\pi \left( {rad/s} \right)\]
+ Cường độ dòng điện cực đại:
I0 = 4(A)
+ Tại t = 0: i = 4
↔ I0cosφ = 4
→ cosφ = 1
→ φ = 0
=>Biểu thức cường độ dòng điện tức thời:
i = 4cos(100πt)A
Đáp án cần chọn là: C
Câu 18:
Đồ thị biểu diễn cường độ tức thời của dòng điện xoay chiều chỉ có cuộn cảm thuần có cảm kháng ZL = 50Ω như hình sau:
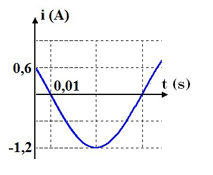
Viết biểu thức điện áp tức thời giữa hai đầu cuộn cảm.
Trả lời:
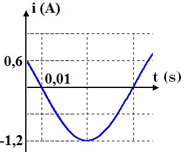
Từ đồ thị ta có:
\[\frac{T}{{12}} = 0,01s \to T = 0,12s\]
\[ \to \omega = \frac{{2\pi }}{T} = \frac{{50\pi }}{3}\left( {rad/s} \right)\]
+ Cường độ dòng điện cực đại:
I0 = 1,2(A)
+ Tại t = 0: I = 0,6A và đang giảm:
i = 0,6 ↔ I0cosφ = 0,6
\[ \to \cos \varphi = \frac{{0,6}}{{1,2}} = \frac{1}{2}\]
\[ \to \varphi = \frac{\pi }{3}\]
=>Biểu thức cường độ dòng điện tức thời:
\[i = 1,2\cos \left( {\frac{{50\pi }}{3}t + \frac{\pi }{3}} \right)A\]
+ Ta có uL nhanh pha hơn i một góc \[\frac{\pi }{2}\]
+ Hiệu điện thế cực đại:
\[{U_0} = {I_0}.{Z_L} = 1,2.50 = 60\left( V \right)\]
=>Biểu thức điện áp tức thời giữa hai đầu cuộn cảm:
\[u = 60\cos \left( {\frac{{50\pi }}{3}t + \frac{\pi }{3} + \frac{\pi }{2}} \right)\]
\[ = 60\cos \left( {\frac{{50\pi }}{3}t + \frac{\pi }{3} + \frac{\pi }{2} + \frac{\pi }{2}} \right)\]
\[ = 60\cos \left( {\frac{{50\pi }}{3}t + \frac{{4\pi }}{3}} \right)V\]
Đáp án cần chọn là: B
Câu 19:
Một đoạn mạch điện xoay chiều gồm R = 60Ω , cuộn cảm thuần \[L = \frac{{0,2}}{\pi }H\]và \[C = \frac{{{{10}^{ - 3}}}}{{8\pi }}F\]mắc nối tiếp. Điện áp giữa hai đầu đoạn mạch là \[u = 100\sqrt 2 \cos 100\pi tV\]. Tìm độ lệch pha giữa điện áp giữa hai đầu đoạn mạch và dòng điện trong mạch?
Trả lời:
Ta có:
\[{Z_L} = \omega L = 100\pi \frac{{0,2}}{\pi } = 20\Omega \]
\[{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 3}}}}{{8\pi }}}} = 80\Omega \]
Độ lệch pha giữa điện áp và cường độ dòng điện trong mạch:
\[\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{20 - 80}}{{60}} = - 1\]
\[ \to \varphi = - \frac{\pi }{4}\]
Đáp án cần chọn là: B
Câu 20:
Đặt điện áp xoay chiều vào hai đầu đọa mạch có R, L, C mắc nối tiếp. Khi trong đoạn mạch có cộng hưởng điện thì điện áp giữa hai đầu đoạn mạch
Trả lời:
Khi trong mạch xảy ra hiện tượng cộng hưởng điện thì: ZL = ZC
=>điện áp giữa hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch
Đáp án cần chọn là: C
Câu 21:
Mạch điện xoay chiều gồm điện trở thuần R = 30Ω mắc nối tiếp với cuộn dây. Đặt vào hai đầu mạch một hiệu điện thế xoay chiều \[u = U\sqrt 2 .\cos \left( {100\pi t} \right)V\] thì hiệu điện thế hiệu dụng ở hai đầu cuộn dây là Ud = 60V và dòng điện trong mạch lệch pha \[\frac{\pi }{6}\] so với u và lệch pha \[\frac{\pi }{3}\] so với udud. Hiệu điện thế hiệu dụng ở hai đầu mạch U có giá trị
Trả lời:
Từ dữ kiện bài cho ta có giản đồ vecto:
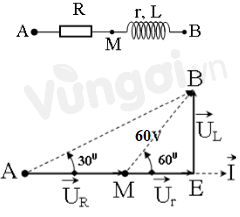
Từ hình vẽ ta có:
\[AMB = 180^\circ - BME = 120^\circ \]
\[ \Rightarrow ABM = 180^\circ - MAB - AMB = 30^\circ \]
⇒ ΔAMB cân tại M
⇒ AM = MB = 60 ⇔ UR = Ud = 60V
Áp dụng định lí hàm số cos trong tam giác AMB có:
\[A{B^2} = A{M^2} + B{M^2} - 2AM.BM.\cos AMB\]
\[ \Leftrightarrow {U^2} = U_R^2 + U_d^2 - 2{U_R}.{U_d}.\cos AMB\]
\[ \Leftrightarrow {U^2} = {60^2} + {60^2} - 260.60.\cos 120 = 10800\]
\[ \Rightarrow U = 60\sqrt 3 V\]
Đáp án cần chọn là: B
