Dạng 3. Tìm số nguyên x thỏa mãn điều kiện về chia hết có đáp án
-
655 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm các số tự nhiên \[{\rm{x}}\]sao cho \[10 \vdots \left( {{\rm{ x - 1}}} \right)\]
Ta có \[10 \vdots \left( {{\rm{ x - 1}}} \right)\] khi đó \[\left( {{\rm{ x - 1}}} \right)\] là ước của 10
\[U\left( {{\rm{10}}} \right){\rm{ = }}\left\{ {{\rm{ \pm 1; \pm 2; \pm 5; \pm 10}}} \right\}{\rm{.}}\]
Ta có bảng sau:

Suy ra \[{\rm{x}} \in \left\{ {{\rm{ 0; 2; 3; 6; 11}}} \right\}\]( \[{\rm{x}} \in \]\(\mathbb{N}\) )
Câu 2:
Câu 3:
\[{{\rm{x}}^{\rm{2}}}{\rm{\; + 2x -- 7}}\,{\rm{ = }}\,{\rm{x(x + 2) - 7}}\]
Ta có: \[{\rm{x}}\left( {{\rm{x + 2}}} \right)\]chia hết cho \[{\rm{x + 2}}\]
Do đó \[{\rm{x}}\left( {{\rm{x + 2}}} \right){\rm{ - 7}}\] chia hết cho \[{\rm{x + 2}}\] khi 7 chia hết cho \[{\rm{x + 2}}\]
Do đó \[{\rm{x + 2}}\] là ước của 7.
Ước của 7 gồm các số \[{\rm{ \pm 1, \pm 7}}\].
Ta có bảng sau:

Suy ra:\[{\rm{x\;}} \in \left\{ {{\rm{ - 9; - 3 ; - 1 ; 5}}} \right\}\].
Câu 4:
Ta có \[{\rm{x + 4 = }}\left( {{\rm{x + 1}}} \right){\rm{ + 3}}\]
nên \[\left( {{\rm{x + 4}}} \right){\rm{ : }}\left( {{\rm{x + 1}}} \right)\] khi \[{\rm{3:}}\left( {{\rm{x + 1}}} \right)\], tức là \[{\rm{x + 1}}\] là ước của 3.
Vì \[U\left( {\rm{3}} \right){\rm{ = \{ - 1 ; 1 ; - 3 ; 3\} }}\], ta có bảng sau:
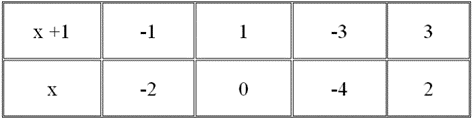
ĐS :\[{\rm{x = - 4 ; - 2 ; 0 ; 2}}\].
Câu 5:
HD: Ta có \[{\rm{4x + 3 = 4}}\left( {{\rm{x -- 2}}} \right){\rm{ + 11}}\]
nên \[\left( {{\rm{4x + 3}}} \right){\rm{ : }}\left( {{\rm{x - 2}}} \right)\] khi \[{\rm{11:}}\left( {{\rm{x - 2}}} \right)\], tức là \[\left( {{\rm{x - 2}}} \right)\] là ước của 11.
Đáp số:\[{\rm{x\;}} \in \left\{ {{\rm{ - 9 ; 1 ; 3 ; 13}}} \right\}\].
Câu 6:
Ta có: \[{{\rm{x}}^{\rm{2}}}{\rm{\; + x + }}\,{\rm{1 = x}}\left( {{\rm{x + 1}}} \right){\rm{ + 1}}\].
Ta có: \[{\rm{x}}\left( {{\rm{x + 1}}} \right)\]chia hết cho \[{\rm{x + 1}}\].
Do đó \[{{\rm{x}}^{\rm{2}}}{\rm{\; + x + }}\,{\rm{1}}\] chia hết cho \[{\rm{x + 1}}\] khi 1 chia hết cho \[{\rm{x + 1}}\], tức là \[{\rm{x + 1}}\] là ước của 1.
Ước của 1 gồm các số \[{\rm{ \pm 1}}\]. Suy ra \[{\rm{x\;}} \in \left\{ {{\rm{0 ; - 2 }}} \right\}\].
Câu 7:
Ta có: \[{\rm{3x -- 8 = 3}}\left( {{\rm{x - 4}}} \right){\rm{ + 4}}\]
Ta có: \[{\rm{3}}\left( {{\rm{x - 4}}} \right)\] chia hết cho \[{\rm{x - 4}}\].
Do đó \[{\rm{3x - 8}}\] chia hết cho \[{\rm{x - 4}}\] khi 4 chia hết cho \[{\rm{x - 4}}\], tức là \[{\rm{x - 4}}\] là ước của 4.
Ước của 4 gồm các số \[{\rm{ \pm 1; \pm 2; \pm 4}}\]. Suy ra \[{\rm{x\;}} \in \left\{ {{\rm{0 ; 2 ; 3 ; 5 ; 6 ; 8 }}} \right\}\].
Câu 8:
Tìm các số tự nhiên x sao cho (x +20) là bội của (x + 2)
\[{\rm{x + 20}}\] là bội của \[{\rm{x + 2}} \Rightarrow \left( {{\rm{x + 20}}} \right) \vdots \left( {{\rm{x + 2}}} \right)\]
\[ \Rightarrow {\rm{x + 20 = }}\left[ {\left( {{\rm{x + 2}}} \right){\rm{ + 18}}} \right] \vdots \left( {{\rm{x + 2}}} \right)\] mà \[\left( {{\rm{x + 2}}} \right) \vdots \left( {{\rm{x + 2}}} \right)\]
Do đó \[18 \vdots \left( {{\rm{x + 2}}} \right) \Rightarrow {\rm{x + 2}} \in {\rm{\"O }}\left( {{\rm{18}}} \right){\rm{ }}\]
\[{\rm{\"O }}\left( {{\rm{18}}} \right){\rm{ = }}\left\{ {{\rm{ \pm 1; \pm 2; \pm 3; \pm 6; \pm 9; \pm 18}}} \right\}\]
Mà \[{\rm{x + 2 }} \ge {\rm{ 2\;}}\]\[{\rm{(x}} \in Z)\] nên \[{\rm{x + 2}} \in \left\{ {{\rm{ 2; 3; 6; 9; 18}}} \right\}\]
\[ \Rightarrow {\rm{x}} \in \left\{ {{\rm{0; 1; 4; 7; 16}}} \right\}\]
Câu 9:
Ta có: \[{\rm{n + 5}}\] chia hết cho \[{\rm{n - 2}}\]
\[ \Rightarrow {\rm{n + 5\; = }}\left( {{\rm{n - 2}}} \right){\rm{ + 7}}\] chia hết cho \[{\rm{n - 2}}\]
Mà \[{\rm{n - 2}}\] chia hết cho \[{\rm{n - 2}}\]
⇒ 7 chia hết cho \[{\rm{n - 2}}\]
\[{\rm{n - 2}}\] thuộc ước của 7
mà \[U\left( {\rm{7}} \right){\rm{ = }}\left\{ {{\rm{ - 7; - 1; 1; 7}}} \right\}\]
\[\begin{array}{l}{\rm{n - 2 = - 7}} \Rightarrow {\rm{n = - 5}}\\{\rm{n - 2 = - 1}} \Rightarrow {\rm{n = 1}}\\{\rm{n - 2 = 1}}\,\, \Rightarrow {\rm{n = 3}}\\{\rm{n - 2 = 7}} \Rightarrow {\rm{n = 9}}\end{array}\]
Vậy \[{\rm{n}} \in \left\{ {{\rm{ - 5; 1; 3; 9}}} \right\}\]
Câu 10:
Tìm số nguyên dương nsao cho 2n là bội của (n - 1).
\[{\rm{2n}}\] là bội của \[{\rm{n - 1}} \Rightarrow {\rm{2n}} \vdots \left( {{\rm{n - 1}}} \right)\]
\[ \Rightarrow {\rm{2n = }}\left[ {{\rm{2}}\left( {{\rm{n - 1}}} \right){\rm{ + 2}}} \right] \vdots \left( {{\rm{ n - 1}}} \right)\]
Mà \[\left( {{\rm{n - 1}}} \right) \vdots \left( {{\rm{n - 1}}} \right)\] . Do đó \[{\rm{2}} \vdots \left( {{\rm{n - 1}}} \right)\]
\[ \Rightarrow {\rm{n - 1}} \in \;U\left( 2 \right){\rm{ }}\]
\[\;U\left( 2 \right){\rm{ = }}\left\{ { \pm 1,{\rm{ }} \pm {\rm{ }}2} \right\}\]
Mà \[{\rm{n - 1 }} \ge {\rm{ 0}}\] nên \[{\rm{n - 1}} \in \left\{ {{\rm{ 1; 2}}} \right\}\]
\[ \Rightarrow {\rm{n}} \in \left\{ {{\rm{2; 3}}} \right\}\]
Câu 11:
\[{\rm{a}}\] chia hết cho \[{\rm{b}}\]\( \Rightarrow \) \[{\rm{a}}\,{\rm{ = }}\,{\rm{b}}{{\rm{q}}_{\rm{1}}}\]\[{\rm{(}}{{\rm{q}}_{\rm{1}}} \in \mathbb{Z},\,b \ne 0)\]
\[{\rm{b}}\]chia hết cho \[{\rm{a}}\]\( \Rightarrow \) \[{\rm{b = a}}{{\rm{q}}_{\rm{2}}}\] \[{\rm{(}}{{\rm{q}}_1} \in \mathbb{Z},\,a \ne 0)\]
\[ \Rightarrow {\rm{a = b}}{{\rm{q}}_{\rm{1}}}{\rm{ = (a}}{{\rm{q}}_{\rm{2}}}{\rm{)}}{{\rm{q}}_{\rm{1}}}{\rm{ = a(}}{{\rm{q}}_{\rm{2}}}{{\rm{q}}_{\rm{1}}}{\rm{)}}\, \Rightarrow {{\rm{q}}_{\rm{2}}}{{\rm{q}}_{\rm{1}}}{\rm{ = 1}}\]
\[ \Rightarrow {{\rm{q}}_{\rm{2}}}{\rm{ = }}\,{{\rm{q}}_{\rm{1}}} = 1\] hoặc \[{{\rm{q}}_{\rm{2}}}{\rm{ = }}\,{{\rm{q}}_{\rm{1}}} = - 1\]
Vì \[{\rm{a}} \ne {\rm{b}}\] nên \[{{\rm{q}}_{\rm{2}}}{\rm{ = }}\,{{\rm{q}}_{\rm{1}}} = - 1\]. Do đó: \[{\rm{a}}\,{\rm{ = }}\,{\rm{b( - 1)}}\,{\rm{ = }}\,{\rm{ - b}}\]
Vậy mọi cặp số nguyên đối nhau và khác 0 đều có tính chất \[{\rm{a}}\] chia hết cho (\[{\rm{ - a}}\]) và (\[{\rm{ - a}}\]) chia hết cho \[{\rm{a}}\] và chỉ những cặp số đó.
Câu 12:
Cho hai tập hợp số: \[{\rm{A = }}\left\{ {{\rm{2 ; 3 ; 4 ; 5 ; 6}}} \right\}{\rm{, B = }}\left\{ {{\rm{21 ; 22 ; 23}}} \right\}{\rm{.}}\]
Có thể lập được bao nhiêu tổng dạng \[\left( {{\rm{a + b}}} \right)\] với \[{\rm{a\;}} \in {\rm{A, b\;}} \in {\rm{B}}\]?
Ta lập bảng cộng sau :
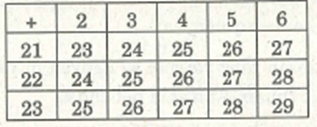
Từ bảng trên, ta thấy có 15 tổng được tạo thành, trong đó có 7 tổng khác nhau:\[{\rm{23, 24, 25, 26, 27, 28, 29}}\].
Câu 13:
Cho hai tập hợp số: A = {2; 3; 4; 5; 6}, B = {21; 22; 23}
Có 7 tổng chia hết cho 2 là : \[{\rm{24 , 24 , 26 , 26 , 26 , 28 , 28}}{\rm{.}}\]
(Có 3 tổng khác nhau chia hết cho 2 :\[24{\rm{ }},{\rm{ }}26{\rm{ }},{\rm{ }}28\]).
Câu 14:
Cho hai tập hợp số \[{\rm{A = }}\left\{ {{\rm{4\;;\;5\;;\;6\;;\;7\;;\;8}}} \right\}{\rm{;\;B = }}\left\{ {{\rm{13\;;\;14\;;\;15}}} \right\}\]
Có thể lập được bao nhiêu tổng dạng \[\left( {{\rm{a + b}}} \right)\] với\[{\rm{a}} \in {\rm{A, b}} \in {\rm{B}}\]?
a) Ta lập bảng cộng sau:
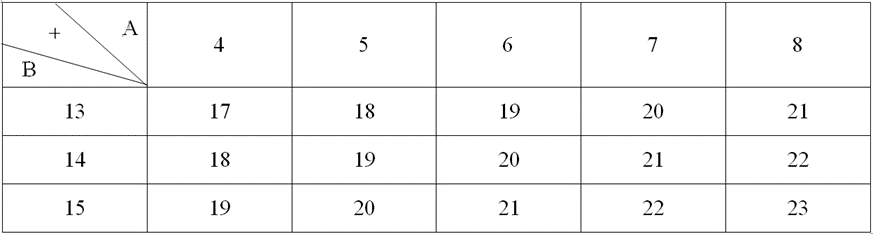
Từ bảng trên, ta thấy có 15 tổng được tạo thành, trong đó có 7 tổng khác nhau :\[{\rm{17, 18, 19, 20, 21, 22, 23}}\].
Câu 15:
Cho hai tập hợp số \[{\rm{A = }}\left\{ {{\rm{4\;;\;5\;;\;6\;;\;7\;;\;8}}} \right\}{\rm{;\;B = }}\left\{ {{\rm{13\;;\;14\;;\;15}}} \right\}\]
Trong các tổng trên có bao nhiêu tổng chia hết cho 3?
Như vậy có hai tổng khác nhau chia hết cho 3 là 18 và 21.
