Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án
Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án (Đề 5)
-
1542 lượt thi
-
62 câu hỏi
-
120 phút
Danh sách câu hỏi
Câu 1:
Thí sinh đọc Bài đọc 1 và trả lời các câu hỏi 1 - 8
BÀI ĐỌC 1
Tầm quan trọng của nghiên cứu khoa học cơ bản đã thể hiện rõ nét hơn bao giờ hết trong những tháng ngày của năm 2020 khi đại dịch Covid-19 đang hoành hành trên khắp thế giới. Nhờ có các nghiên cứu cơ bản, cụ thể là các nghiên cứu khám phá về virus, con người đã nhanh chóng xác định được các đặc trưng cơ bản cũng như cách chúng phát triển, lây lan và tấn công cơ thể con người. Từ đó, các chính phủ, dựa trên các khuyến nghị từ các nhà khoa học, đã đưa ra các phương án kịp thời và hiệu quả để bảo vệ người dân như giãn cách xã hội hay đeo khẩu trang ở nơi công cộng.
Tuy nhiên, đó chỉ là các phương án tạm thời. Thế giới cần có biện pháp hiệu quả và bền vững hơn, và đó chính là vaccine. Các phương pháp chế tạo vaccine truyền thống cần một thời gian tương đối dài, cỡ 10 năm, và do đó không đáp ứng được nhu cầu cấp bách hiện nay. Rất may, các nghiên cứu khoa học đột phá về mRNA của nhà khoa học người Hungary, TS. Katalin Kariko, tiến hành vào năm 2005 khi bà làm việc tại Đại học Pennsylvania, đã trở thành chìa khóa để giúp các nhà nghiên cứu của Công ty BioNTech, có trụ sở tại thành phố Mainz, nước Đức tìm ra vaccine chỉ trong vòng một thời gian kỷ lục 10 tháng, thay vì 10 năm.
Trước khi Covid-19 nổ ra, các nghiên cứu của TS. Katalin Kariko từng bị hoài nghi. Có lẽ chính TS. Katalin Kariko cũng không thể nghĩ được rằng các nghiên cứu táo bạo của mình lại trở thành phép màu cho cả thế giới 15 năm sau. Như nhà khoa học đoạt giải Nobel về Sinh lý học và Y học năm 1993, Richard Roberts, đã từng nói “Vẻ đẹp của nghiên cứu khoa học thể hiện ở chỗ bạn không bao giờ biết được nó sẽ dẫn đến đâu”. Hay như nhà khoa học đoạt giải Nobel Vật lý năm 2012, Serge Haroche, đã từng nói “Ngay cả những người thông minh nhất cũng không thể hình dung ra hết các hệ quả của nghiên cứu mà họ tiến hành”. Trong số hàng trăm nghiên cứu lớn nhỏ của TS. Katalin Kariko, chỉ cần một trong số chúng nhen nhóm hi vọng hồi sinh cho cả thế giới thì còn gì tuyệt vời hơn?
Từ câu chuyện về vaccine Covid-19, chúng ta thấy rằng cần phải có một tư duy hệ thống, sâu sắc và dài hạn cho nghiên cứu cơ bản. Nghiên cứu cơ bản là các nghiên cứu đi sâu vào tìm hiểu bản chất và quy luật vận động của các sự vật, hiện tượng tự nhiên. Các kết quả của nó mang tính nguyên bản. Động lực để phát triển nó đó chính là sự tò mò của con người. Mọi quá trình nóng vội mang tính thời vụ đều không phù hợp với các nghiên cứu cơ bản.
Khi Newton nghiên cứu và xây dựng nên lý thuyết hấp dẫn, mục tiêu của ông đó là giải thích được câu hỏi “tại sao quả táo rơi xuống đất thay vì bay lên trời?”. Nhưng sau đó, chính ông và nhiều nhà khoa học khác thấy được lý thuyết hấp dẫn này còn giải thích và tiên đoán được vô số hiện tượng khác xảy ra trong tự nhiên và vũ trụ. Cơ học Newton đã thành nền tảng lý thuyết để các kỹ sư chế tạo nên máy móc, phương tiện giao thông, cầu đường, nhà cửa. Thiếu nó, mọi hoạt động con người sẽ không còn trơn tru và hiệu quả. Thiếu nó, bạn sẽ không có một chiếc xe Vinfast chạy nhanh và êm ái được.
Khi Planck đề xuất thuyết lượng tử, mục tiêu của ông đó là giải quyết vấn đề chưa có lời giải về phổ bức xạ của vật đen tuyệt đối. Và chắc chắn ông không thể hình dung lý thuyết của mình trở thành một trong hai trụ cột chính của Vật lý hiện đại. Nhờ có lý thuyết lượng tử mà con người ngày hôm nay có các máy tính cá nhân, các điện thoại thông minh, hay các tấm pin năng lượng mặt trời. Nhờ có thuyết lượng tử mà chúng ta có thời đại công nghiệp 4.0. Thiếu nó chúng ta không thể có các tập đoàn công nghệ lớn mạnh như Viettel.
Vào thời điểm này, đại dich Covid-19 vẫn là câu chuyện đang rất nóng hổi. Chúng ta nên biết rằng nếu không có các nghiên cứu khám phá về cấu trúc DNA đầu tiên của Francis Crick, James Watson, và Rosalind Franklin cách đây 67 năm thì chúng ta sẽ không có vaccine Covid-19 nhanh như bây giờ. Chúng ta cần nhớ có rất nhiều loại virus khác nhau tồn tại trong tự nhiên. Hôm nay virus này đến từ con dơi, nhưng ngày mai virus khác có khi lại đến từ một con chim hót rất hay. Chúng ta cần phải chuẩn bị cho các đại dịch có thể xảy ra trong tương lai. Đầu tư cho khoa học cơ bản đề duy trì một đội ngũ các nhà khoa học tài năng, am tường các tiến bộ khoa học – công nghệ của nhân loại là một cách chuẩn bị khôn ngoan nhất. Trong quá khứ, một dân tộc thiện chiến có thể thống lĩnh cả thế giới. Nhưng trong tương lai, một dân tộc tồn tại được dài lâu hay không phụ thuộc vào việc dân tộc đó uyên bác đến mức độ nào.
(Theo Đỗ Quốc Tuấn, Khoa học cơ bản: Giữa vẻ đẹp và tính hữu ích, Báo Khoa học & Phát triển, ngày 11/02/2021)Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?
Đáp án A
Ý chính của các đoạn trong bài:
Đoạn 1: Tầm quan trọng của nghiên cứu khoa học thể hiện rõ nét nhất trong đại dịch Covid-19.
Đoạn 2: Nghiên cứu tìm ra mRNA giúp rút ngắn thời gian phát triển vaccine Covid-19.
Đoạn 3: “Vẻ đẹp cảu nghiên cứu khoa học thể hiện ở chỗ bạn không bao giờ biết được nó sẽ dẫn đến đâu”.
Đoạn 4: Cần phải có một tư duy hệ thống, sâu sắc và dài hạn cho nghiên cứu cơ bản.
Đoạn 5: Ý nghĩa của lý thuyết hấp dẫn.
Đoạn 6: Ý nghĩa của lý thuyết lượng tử.
Đoạn 7: Ý nghĩa của nghiên cứu khoa học cơ bản.
Tổng hợp các ý trên, ta có ý nghĩa chính của toàn bài là: “Nêu bật vai trò và ý nghĩa của nghiên cứu khoa học cơ bản”.
Câu 2:
Theo tác giả, đại dịch Covid-19 đã:
Đáp án B
Thông tin tại dòng 5-6: “Từ đó, các chính phủ, dựa trên các khuyến nghị từ các nhà khoa học”.
Câu 3:
Ý nào sau đây là một trong “các phương án tạm thời” được đề cập ở dòng 8?
Đáp án B
Giãn cách xã hội trên diện rộng là một trong các biện pháp tạm thời được đề cập ở câu liền trước.
Câu 4:
Tại đoạn 3 (dòng 19-21), câu văn “Vẻ đẹp của nghiên cứu khoa học thể hiện ở chỗ bạn không bao giờ biết được nó sẽ dẫn đến đâu” minh họa tốt nhất cho ý nào sau đây?
Đáp án C
Câu văn “Vẻ đẹp của nghiên cứu khoa học thể hiện ở chỗ bạn không bao giờ biết được nó sẽ dẫn đến đâu” thể hiện ý: vẻ đẹp của nghiên cứu khoa học là các nhà khoa học không biết mình sẽ nhận được lợi ích gì (vật chất, danh tiếng...) khi tiến hành nghiên cứu. Ý này được thể hiện rõ hơn ở dòng 27-30: “Nghiên cứu cơ bản là các nghiên cứu đi sâu vào tìm hiểu bản chất và quy luật vận động của các sự vật, hiện tượng tự nhiên. Các kết quả của nó mang tính nguyên bản. Động lực để phát triển nó đó chính là sự tò mò của con người”.
Câu 5:
Vì sao tác giả cho rằng: “Từ câu chuyện về vaccine Covid-19, chúng ta thấy rằng cần phải có một tư duy hệ thống, sâu sắc và dài hạn cho nghiên cứu cơ bản”?
Đáp án D
Ở đây tác giả muốn nhấn mạnh các nghiên cứu cơ bản được khám phá ra từ trước là tiền đề quan trọng cho các biện phát phòng chống Covid-19 hiện nay. Chúng ta cần tiếp tục tiến hành các nghiên cứu cơ bản một hệ thống và lâu dài cho các sự cố bất ngờ trong tương lai.
Câu 6:
Tác giả nhắc đến hình ảnh “một chiếc xe Vinfast” ở dòng 38 nhằm mục đích gì?
Đáp án D
Ở đây, tác giả muốn nhấn mạnh không có lý thuyết hấp dẫn thì Vinfast không thể chế tạo được xe hơi, chiếc xe hơi là một hệ quả của lý thuyết (mà Newton không thể lường đến được khi ông tiến hành nghiên cứu).
Câu 7:
Mục tiêu của Max Planck khi đề xuất thuyết lượng tử là gì?
Đáp án A
Thông tin tại dòng 40-41: “Khi Planck đề xuất thuyết lượng tử, mục tiêu của ông đó là giải quyết vấn đề chưa có lời giải về phổ bức xạ của vật đen tuyệt đối”. Các phương án còn lại mà hệ quả từ lý thuyết lượng tử mà Planck tính toán khi tiến hành nghiên cứu.
Câu 8:
Tác giả cho rằng sự sống còn của một dân tộc phụ thuộc chính vào yếu tố nào sau đây?
Đáp án A
Thông tin tại dòng 56-57: “Nhưng trong tương lai, một dân tộc tồn tại được lâu dài hay không phụ thuộc vào việc dân tộc đó uyên bác đến mức độ nào”.
Câu 9:
Thí sinh đọc Bài đọc 2 và trả lời câu hỏi 9 - 16
BÀI ĐỌC 2
Tốt nghiệp Khoa Công nghệ thông tin tại Đại học Bách khoa Hà Nội năm 2021, Phạm Giang Linh – Tổng giám đốc Hệ thống Giáo dục HOCMAI – có hơn 10 năm làm việc ở vị trí chuyên gia tư vấn về quản trị, giám sát đánh giá và quản lý thông tin của các dự án phát triển con người và chính sách công trong khu vực ASEAN tại nhiều tổ chức quốc tế. Ngoài ra anh còn là đồng sáng lập của nhiều doanh nghiệp khác. Tuy nhiên Phạm Giang Linh lại chọn HOCMAI làm bến đỗ lâu dài với ước mơ tạo cơ hội tiếp cận giáo dục chất lượng cao, bình đẳng cho mọi học sinh.
Hocmai.vn ra đời tháng 3/2007, cùng thời với một tên tuổi khác là Topica, nhưng khi đó, cả hai hệ thống này đều gặp trở ngại vì mô hình giáo dục trực tuyến chưa được thị trường đón nhận.
Là người quê gốc Ninh Bình lên Hà Nội học tập, Giang Linh thấm thía cảnh hàng trăm học sinh “nhồi nhét” trong các “lò luyện thi” để nghe giáo viên giảng bài mà không rõ các em lĩnh hội được bao nhiêu.
“Với một lớp 30 – 50 học sinh, giáo viên chỉ có thể dạy theo tốc độ của 3 học sinh top đầu, hoặc top cuối. Đó là một trong những hạn chế lớn nhất của giáo dục truyền thống. Trong khi đó, giáo dục trực tuyến có thể đáp ứng được tốc độ học của từng cá nhân, học sinh còn có thể học đi học lại, những phần bài giảng mà mình không hiểu. Tôi muốn theo đuổi mô hình giúp thúc đẩy tính tự học và tình yêu học tập của trẻ em, với tâm niệm đóng góp điều gì đó tích cực cho nền giáo dục Việt Nam”, Giang Linh nói.
Trong khi nhiều start-up ưu tiên đầu tư cho công nghệ, thì HOCMAI lại đầu tư nhiều vào sản phẩm giáo dục. Bản chất của giáo dục là tương tác giữa người với người, còn công nghệ chỉ là cách thức để truyền tải nội dung đến học sinh. Đó là lý do trong số 300 nhân viên của HOCMAI, có tới 2/3 làm ở mảng nội dung. Với tiêu chí tập trung vào sản phẩm, mô hình HOCMAI giống như trường học số với đầy đủ bộ phận thiết kế, phát triển chương trình, đánh giá nhu cầu học tập, lộ trình những khóa học…
Theo Giang Linh, lợi ích lớn nhất của giáo dục trực tuyến là chi phí rẻ, nhưng để có lợi nhuận, các dự án này phải tạo ra hệ sinh thái người học đủ lớn. Học trực tuyến không có sự thúc ép, nên nếu chất lượng sản phẩm học liệu không đủ tốt, thương hiệu không đủ mạnh, thì sẽ không ai học. Các bài giảng cũng cần phải được thiết kế dễ hiểu bằng cách dùng công nghệ để mô phỏng các thuật toán, kiến thức khó để học sinh có cảm giác đang khám phá, chứ không phải là nhồi nhét những kiến thức khô khan.
Mặt khác tâm lý e ngại của thị trường đối với cách thức giảng dạy mới mẻ này chính là rào cản lớn nhất cho những đơn vị đầu tư giáo dục trực tuyến không đủ kiên trì. Bởi lẽ đầu tư giáo dục trực tuyến không dễ thành công nhanh chóng “qua một đêm”. “Về bản chất, mặc dù đầu tư giáo dục trực tuyến không phụ thuộc vị trí địa lý, không cần quá nhiều vốn ban đầu, quy mô không hạn chế, khi thành công có thể phát triển mô hình ra thị trường quốc tế, nhưng nếu không đảm bảo chất lượng và giữ được thương hiệu, sự kiên trì, thì dự án dễ đi đến thất bại”, Giang Linh phân tích.
Anh lấy ví dụ, ở Trung Quốc có hàng chục mô hình đầu tư giáo dục trực tuyến. Trong khi đó, ở Việt Nam, mô hình đầu tư truyền thống vẫn là kênh thu hút nhiều nhà đầu tư với công thức tính lợi nhuận thông thường khoảng 20 – 50%, còn đầu tư trực tuyến thì chạy mãi mà … không nhìn thấy lợi nhuận.
“Nhiều người nói với tôi rằng, ổn định rồi thì cứ thế phát triển, việc gì phải thay đổi. Nhưng, bạn hãy nhìn một đứa trẻ phát triển và thay đổi từng ngày, HOCMAI cũng như một cơ thể sống, nếu không thay đổi là tự tìm đường đến cái chết. Với mô hình giáo dục truyền thống, giáo viên có thể sai sót và có thể sửa, nhưng giáo dục trực tuyến thì không có chỗ cho sai sót”, Giang Linh nhấn mạnh.
Gần đây nhất, HOCMAI hợp tác với Funix để dạy lập trình cho học sinh từ lớp 6 đến lớp 12 với mục tiêu hướng học sinh không có nhu cầu học đại học có thể đi làm ngay. Một dự án khác là chương trình dạy tiếng Anh 1-1 với người nước ngoài cũng đang được triển khai tại HOCMAI từ hơn 1 năm nay.
Về mục tiêu của HOCMAI, Giang Linh chia sẻ: “Giáo dục Việt Nam còn nhiều vấn đề cần giải quyết. Nếu hệ thống trực tuyến của chúng tôi không giải quyết được những khiếm khuyết hiện có, thì việc mở rộng cấp cao hơn cũng không nhiều ý nghĩa. Thị trường 17 triệu học sinh phổ thông còn rất nhiều tiềm năng và dư địa để khai thác. Chúng tôi cần sớm khẳng định thương hiệu trước khi các đơn vị nước ngoài nhảy vào”.
Tầm nhìn của người đứng đầu hệ thống này cũng sẽ không dừng lại ở thị trường Việt Nam. Trong 3 – 5 năm tới, Philippines và Indonesia sẽ là đích ngắm của HOCMAI. Đây là 2 quốc gia có dung lượng thị trường đủ lớn cho khai thác giáo dục trực tuyến.
(Theo Trần Hà, Phạm Giang Linh, Tổng giám đốc HOCMAI: Đầu tư giáo dục trực tuyến không dễ thành công sau một đêm, Báo Đầu tư, ngày 29/01/2020)Đáp án B
Ý chính của các đoạn trong bài:
Đoạn 1: Giới thiệu ông Phạm Giang Linh – Tổng giám đốc Hocmai.vn.
Đoạn 2: Giới thiệu Hocmai.vn
Đoạn 3-4: Lí do ông Phạm Giang Linh tham gia làm việc tại HOCMAI.
Đoạn 5-6: Đặc điểm của giáo dục trực tuyến và chiến lược của Hocmai.vn.
Đoạn 7-8: Những thách thức cản trở sự phát triển của giáo dục trực tuyến ở Việt Nam
Đoạn 9-12: Định hướng phát triển của HOCMAI trong tương lai.
Tổng hợp các ý trên, ta có ý chính của toàn bài là: “Đầu tư giáo dục trực tuyến không đơn giản – bài học từ Hocmai.vn”.
Câu 10:
Thông tin nào sau đây KHÔNG chính xác?
Đáp án B
Thông tin tại dòng 5-6: “Anh còn là đồng sáng lập của nhiều doanh nghiệp khác. Tuy nhiên Phạm Giang Linh lại chọn HOCMAI làm bến đỗ lâu dài...” => Đoạn trích không đề cập Phạm Giang Linh là đồng sáng lập của HOCMAI. Mặt khác cụm “...chọn HOCMAI làm bến đỗ lâu dài...” hàm ý Phạm Giang Linh gia nhập sau khi HOCMAI đã thành lập một thời gian.
Câu 11:
Ông Phạm Giang Linh cho rằng nhược điểm chính của giáo dục truyền thống là gì?
Đáp án B
Thông tin tại dòng 14-16: “Với một lớp 30-50 học sinh, giáo viên chỉ có thể dạy theo tốc độ của 3 học sinh top đầu, hoặc top cuối. Đó là một trong những hạn chế lớn nhất của giáo dục truyền thống”.
Câu 12:
Đáp án C
Thông tin tại dòng 21-22: “Bản chất của giáo dục là tương tác giữa người với người, còn công nghệ chỉ là cách thức để truyền tải một nội dung đến học sinh”.
Câu 13:
Theo ông Phạm Giang Linh, các đơn vị giáo dục trực tuyến cần thu hút người học bằng cách nào?
Đáp án D
Thông tin tại dòng 28-29: “...nếu chất lượng sản phẩm học liệu không đủ tốt, thương hiệu không đủ mạnh, thì sẽ không ai học”.
Câu 14:
Ý nào sau đây là một tính chất của giáo dục trực tuyến?
Đáp án D
Thông tin tại dòng 34-35: “... đầu tư giáo dục trực tuyến không dễ thành công nhanh chóng “qua một đêm”.” => cần có kế hoạch lâu dài.
Câu 15:
Cụm từ “dư địa” ở dòng 55 mang ý nghĩa gì?
Đáp án A
Dư địa có nghĩa đen là phần đất còn trống, nghĩa bóng trong ngữ cảnh này là phần thị trường chưa có ai chiếm lĩnh.
Câu 16:
Đáp án B
Thông tin tại dòng 53-55: “Nếu hệ thống trực tuyến của chúng tôi không giải quyết được những khiếm khuyết hiện có, thì việc mở rộng cấp cao hơn cũng không nhiều ý nghĩa. Thị trường 17 triệu học sinh phổ thông còn rất nhiều tiềm năng và dư địa để khai thác”. => HOCMAI sẽ tập trung giải quyết các vấn đề của giáo dục phổ thông, chưa có kế hoạch mở rộng ra các cấp học khác.
Câu 17:
Mới đây nhóm nghiên cứu của PGS.TS Đỗ Văn Mạnh, Viện Công nghệ môi trường, Viện Hàn lâm Khoa học và Công nghệ Việt Nam đã triển khai thành công hệ thống xử lý bùn thải thành phân hữu cơ và khí biogas, với công suất phát điện đạt 20kW, tại thành phố Buôn Mê Thuột, Đắk Lắk.
Công nghệ này được nhóm bắt đầu nghiên cứu từ năm 2016, trong Chương trình nghiên cứu khoa học công nghệ theo Nghị định thư do Bộ Khoa học và Công nghệ chủ trì, với mục tiêu xây dựng quy trình công nghệ xử lý bùn thải hiệu quả ở quy mô công nghiệp, tạo ra những sản phẩm nông nghiệp có giá trị bền vững.
So với các quy trình xử lý truyền thống, công nghệ cho hiệu suất chuyển hóa bùn thải thành khí sinh học cao, giúp rút ngắn thời gian xử lý trong khoảng 15-20 ngày. Đặc biệt, hai sản phẩm thu được sau quá trình xử lý gồm khí biogas và phân bón sinh học đều đạt tiêu chuẩn sử dụng làm nguyên liệu cho sản xuất. Khí biogas sinh ra được dùng làm nguyên liệu cho máy phát điện, đáp ứng tiêu chuẩn nhiên liệu của châu Âu.
TS Mạnh cho biết, bùn thải đưa vào bể tiền xử lý để điều chỉnh độ pH và các thông số khác trước khi đưa vào bể xử lý chính. Công đoạn này tạo điều kiện tốt nhất cho các nhóm vi sinh vật thực hiện quá trình phân hủy bùn thải yếm khí, có thể giảm độ pH bằng axit hoặc dùng bazo để tăng pH.
Sau bước tiền xử lý, nhóm tiến hành phân hủy yếm khí bùn thải để tạo ra khí biogas. Tuy nhiên, khí biogas sau khi được rạo ra vẫn còn nhiều tạp chất (CO2, H2S, SO2), có thể gây kết tinh trong buồng đốt hoặc ăn mòn các đường dẫn,bình chứa nhiên liệu cũng như bếp đốt. Vì vậy, TS Mạnh và cộng sự đã tự chế tạo và thiết kế thành công được thiết bị lọc quay ly tâm tốc độ cao để làm sạch khí sinh học trước khi nạp vào hệ thống máy phát điện, nhờ vậy nhóm nghiên cứu đã giải mã thành công công nghệ do Đài Loan chuyển giao.
Biogas được đưa vào máy ly tâm tốc độ cao HGRPB để loại bỏ tạp chất bằng dung dịch hấp thụ KOH. Dưới tác động của cơ quay trục giữa, dung dịch KOH được chuyển động ly tâm với tốc độ cao, làm tăng cường quá trình tiếp xúc giữa dung dịch hấp thụ và dòng khí đi vào. Nhờ vậy, dung dịch hấp thụ không bị kéo ra ngoài theo dòng khí, giúp biogas sau khi xử lý có độ ẩm và đạt tiêu chuẩn dành cho phát điện.
“Công đoạn quan trọng nhất nằm ở kỹ thuật điều chỉnh chế độ công nghệ để gia tăng hiệu suất chuyển hóa từ bùn hữu cơ sang khí sinh học hiệu quả cao. Thiết bị do nhóm thiết kế cho ưu điểm nhỏ gọn hơn, được tạo ra từ vật liệu dễ tìm, phù hợp với điều kiện trong nước”, TS Mạnh nói và cho biết, thiết bị có khả năng phát hiện thời gian bão hòa của khí, phản ứng tiếp xúc nhanh, thu được khí biogas sạch gần như 100%, đạt tiêu chuẩn làm nhiên liệu phát điện.
Nhóm đã đưa công nghệ ứng dụng xử lý bùn thải tại một doanh nghiệp sản xuất bia tại Đắk Lắk, toàn bộ 15m3 bùn mỗi ngày được xử lý để phát điện với công suất 20kW. Lượng điện này phục vụ lại vận hành máy bơm, các thiết bị xử lý của hệ thống hoặc đèn chiếu sáng trong các trang trại rau.
Lượng bùn thải sau quá trình phân hủy còn lại được phối trộn với các thành phần vi lượng và vi sinh vật để tạo phân bón hữu cơ sinh học giúp đất tăng độ ẩm và độ tơi xốp, nâng cao hiệu quả sử dụng phân. Loại phân hữu cơ được bón cho cây rau ngắn ngày cho chất lượng tốt, hạn chế sâu bệnh và tăng năng suất.
Bùn thải từ các hoạt động sản xuất, chứa rất nhiều các tế bào vi sinh vật và hỗn hợp các protein, polisaccarit, lipit. Hiện nay, việc xử lý bùn thải tại Việt Nam mới chỉ áp dụng phương pháp ủ hoặc chôn lấp, chưa có hệ thống công nghệ xử lý hoàn thiện ở quy mô lớn, kết hợp với xử lý chất thải rắn. Nếu không được xử lý kịp thời, khối lượng lớn bùn thải sẽ gây ảnh hưởng nghiêm trọng môi trường.
“Công nghệ xử lý bùn thải được nhóm hoàn thiện với mục tiêu vừa có thể hạn chế thải các chất ô nhiễm ra ngoài môi trường, vừa tạo ra những sản phẩm giá trị như khí biogas, phân bón hữu cơ. Từ đó góp phần tạo nên một nền nông nghiệp tuần hoàn, bền vững”, TS Mạnh nói.
Tuy nhiên đây mới là thành công ở quy mô xử lý nhỏ. Để có thể phát triển hệ thống ở quy mô bán công nghiệp với khối lượng 80 tấn, đem lại hiệu quả cao, nhóm nghiên cứu cho rằng cần phải làm chủ công nghệ và có sự phối hợp giữa các bên liên quan trong việc xây dựng những nhà máy xử lý bùn thải tại các thành phố, khu công nghiệp lớn.
(Theo Nguyễn Xuân, Công nghệ xử lý bùn thải tạo khí sinh học phát điện, Báo VN Express, ngày 21/11/2020)Đáp án A
Ý chính của các đoạn trong bài:
Đoạn 1-3: Giới thiệu nghiên cứu công nghệ xử lí bùn thải của nhóm PGS.TS. Đỗ Văn Mạnh.
Đoạn 4-7: Các bước trong quy trình xử lí bùn thải hữu cơ.
Đoạn 8-10: Các kết quả của nghiên cứu công nghệ xử lí bùn thải/
Tổng hợp các ý trên, ta có ý chính của toàn bài là: “Phát triển công nghệ xử lí bùn thải tạo khí sinh học phát điện tại Tây Nguyên”.
Câu 18:
Ý nào sau đây KHÔNG phải là một trong các ưu điểm của công nghệ xử lý bùn thải mới do nhóm PGS.TS Đỗ Văn Mạnh nghiên cứu?
Đáp án D
Ưu điểm của công nghệ này được đề cập tại dòng 9-13. Trong đó không nhắc đến thời gian xây dựng để xử lý bùn thải.
Câu 19:
Vai trò chính của bể tiền xử lý là gì?
Đáp án A
Thông tin tại dòng 14-15: “TS.Mạnh cho biết, bùn thải được đưa vào bể tiền xử lý để điều chỉnh độ pH và các thông số khác trước khi đưa vào bể xử lý chính”.
Câu 20:
“đường dẫn, bình chứa nhiên liệu cũng như bếp đốt” được nhắc tới ở dòng 20-21 là các bộ phận của thiết bị nào sau đây?
Đáp án D
Các bộ phận như “bình chứa nhiên liệu”, “bếp đốt” là thiết bị phục vụ cho quá trình đốt cháy khí biogas chỉ có trong chu trình hoạt động của máy phát điện. Chu trình đốt cháy không xuất hiện trong cơ chế hoạt động của các thiết bị còn lại như bể chứa hay máy ly tâm.
Câu 21:
Dung dịch KOH đóng vai trò gì trong quy trình đưa khí Biogas đi qua máy ly tâm HGRPB?
Đáp án A
Theo đoạn trích, KOH có tác dụng hòa tan các tạp chất có trong dòng khí biogas, do đó KOH đóng vai trò dung môi.
Câu 22:
Cụm từ “khí biogas sạch” ở dòng 34 có thành phần chính là chất nào sau đây?
Đáp án C
Thông tin tại dòng 18-19: “Sau bước tiền xử lý, nhóm tiến hành phân hủy yếm khí bùn thải để tạo ra khí biogas CH4”.
Câu 23:
Đáp án C
Các ưu điểm của phân bón sinh học sinh ra từ công nghệ xử lí bún thải được nhắc tới tại dòng 40-43, trong đó không đề cập thời gian thu hoạch.
Câu 24:
Ý chính của đoạn 10 (dòng 44-48) là gì?
Đáp án B
Đoạn 10 gồm 3 câu:
Câu 1: Thành phần của bùn thải hữu cơ.
Câu 2: Hiện trạng công nghệ xử lí bùn thải ở Việt Nam hiện nay.
Câu 3: Tác động của bùn thải không được xử lí đến môi trường.
Do đó, ý chính của cả đoạn là: “Thực trạng công nghệ xử lí bùn thải hữu cơ ở Việt Nam”.
Câu 25:
Đáp án B
Thông tin tại dong 53: “Tuy nhiên đây mới là thành công ở quy mô xử lý nhỏ”.
Câu 26:
Ngày 20.07.1969 Neil Armstrong đặt chân lên Mặt Trăng, đánh dấu cột mốc quan trọng của nhân loại. Nhưng đằng sau đó là một cuộc đua quyết liệt giữa Mỹ và Liên Xô.
Công nghệ tên lửa vũ trụ hiện đại được khởi nguồn từ Viện nghiên cứu quân sự của Đức Quốc xã với giám đốc kỹ thuật Wernher von Braun khi đó tuổi đời còn rất trẻ. Đỉnh cao trong sự nghiệp của ông là việc phát triển thành công tên lửa cỡ lớn dài 14 mét có tên V2. Tháng 10/1942 V2 được phóng thành công lên tới độ cao 84,5 km (vượt qua ranh giới bầu khí quyển 80km – theo tiêu chuẩn của NASA hiện nay), và đạt đến độ cao 174,6 km hai năm sau đó. Từ năm 1944, tên lửa này bị coi là mối nguy tiềm tàng đối với nhiều nước.
Cả người Nga và người Mỹ đều ý thức được sự vượt trội về công nghệ tên lửa của Đức. Khi chiến tranh kết thúc vào năm 1945, họ đã tìm mọi cách vơ vét tất cả những gì liên quan đến tên lửa V2. Ngay đến bảo tàng của Đức ở Peenemunde cũng chỉ có bản sao của V2 để giới thiệu với công chúng.
Người ta không chỉ lấy đi các nguyên liệu, bản vẽ mà cả những tác giả của công nghệ tên lửa. Những chuyên gia tên lửa hàng đầu của Đức đã cùng với Wernher von Braun nhanh chóng chạy về vùng Bayern để đầu hàng quân đội Mỹ. Một số người khác, tài năng không kém, thì rơi vào tay quân Nga. Nhưng bọn họ đã nhanh chóng được thả sau khi khai báo mọi thông tin cho Sergei Pavlovich Korolev (1906-1966).
Sergei Pavlovich Korolev có một thời gian dài ở Đông Đức để nghiên cứu về V2, nhờ đó ông đã phát triển thành công tên lửa R1 của Liên Xô. Không lâu sau đó cuộc chạy đua phát triển tên lửa liên lục địa quân sự giữa Mỹ và Liên Xô đã nổ ra đều dựa trên nền tảng V2.
Bước ngoặt xảy ra khi Liên Xô phóng “Sputnik 1” năm 1957. Nó trở thành cú sốc lớn đối với nước Mỹ. Sau đó Liên Xô tiếp tục dẫn trước: “Luna 2” thực hiện chuyến hạ cánh cứng đầu tiên lên Mặt Trăng vào năm 1959, Yuri Gagarin là người đầu tiên bay quanh Trái Đất vào năm 1961 trên tàu vũ trụ “Vostok 1”.
Để đối chọi với “Sputnik” Mỹ tung ra dự án “Vanguard”. Tuy nhiên đây là một thất bại, trong số 12 cuộc phóng thì 9 không thành công. Các chuyên gia tên lửa của Đức không tham gia dự án này, họ được giao phát triển tên lửa quân sự Redstone trên nền tảng V2.
1961 là năm bản lề đối với hành trình chinh phục Mặt Trăng của loài người. Ngày 25.05.1961, Tổng thống Kennedy tuyên bố mục tiêu ngay trong thập niên này sẽ đưa người lên Mặt Trăng và trở về an toàn. Đây là một dự án đầy tham vọng và vô cùng tốn kém nhưng được khích lệ bởi quyết tâm không để thua Liên Xô một lần nữa.
Cũng trong năm đó Liên Xô đưa ra một chương trình Mặt Trăng tương tự, nhưng giữ bí mật. Chương trình chinh phục Mặt Trăng Apollo của Mỹ do Cơ quan không gian dân dụng NASA, ra đời năm 1958, chịu trách nhiệm. Wernher von Braun và đội ngũ của ông đóng một vai trò then chốt cho dù NASA thời kỳ đầu có tới 450.000 nhân sự tham gia giải quyết một khối lượng công việc khổng lồ mà thoạt đầu tưởng chừng không thể kham nổi.
Von Braun có nhiệm vụ phát triển tên lửa Saturn V với chiều cao 111 mét, cho đến nay vẫn là loại tên lửa đẩy lớn nhất thế giới. Các bộ phận riêng lẻ được lắp ráp với nhau trong một nhà xưởng cao tới 160 mét ở Trung tâm Vũ trụ John F. Kennedy (KFC). Ngay trong chuyến bay thử đầu tiên vào ngày 9.11.1967 Saturn V đã thành công. Có thể nói toàn bộ chương trình tên lửa đẩy khổng lồ của Mỹ hầu như không gặp trục trặc đáng kể nào. Phải chăng von Braun và các cộng sự của ông đã gặp nhiều may mắn? Nhưng, may mắn chỉ đến với những người thực sự tài năng và có quyết tâm.
Trong khi đó Liên Xô vẫn lặng lẽ bí mật xúc tiến chương trình của mình. Đối thủ của Apollo khi đó là tàu vũ trụ Sojus, vẫn còn hoạt động cho tới ngày nay. Ngay trong chuyến bay đầu tiên đã xảy ra một tai nạn chết người, khi hạ cánh dù không hoạt động. Để phục vụ cho các chuyến bay lên Mặt Trăng, Liên Xô dự định sử dụng loại tên lửa đẩy N1, cao 105 mét. Trong khi dự án đang được triển khai, ngành du hành vũ trụ Liên Xô đã bị một cú đánh trời giáng. Tổng công trình sư thiên tài Sergei Pavlovich Korolev qua đời vào năm 1966 trong một ca phẫu thuật bệnh tim.
Hai kỳ phùng địch thủ Korolev và von Braun nay đã chỉ còn lại một. Nếu như Korolev không phải rời khỏi cuộc đua vì bệnh tật và cái chết, điều gì sẽ xảy ra?
Sau đó thì phía Liên Xô ngày càng bế tắc. Tất cả bốn cuộc thử tên lửa từ 1969 đến 1972 đều trục trặc, không thành công, đến đây cuộc chạy đua coi như đã bị thất bại, Liên Xô ngừng chương trình Mặt Trăng.
(Theo Xuân Hoài lược dịch, Lịch sử cuộc đua lên Mặt Trăng, Tạp chí Tia sáng, ngày 08/03/2021)Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?
Đáp án A
Ý chính của các đoạn trong bài:
Đoạn 1: Giới thiệu cuộc đua chinh phục Mặt Trăng của Liên Xô và Mỹ.
Đoạn 2-4: Công nghệ tên lửa của Đức Quốc Xã và cuộc tranh giành của Liên Xô và Mỹ.
Đoạn 5-6: Những thành công ban đầu của chương trình tên lửa và hàng không vũ trụ Liên Xô.
Đoạn 7-10: Mỹ phát triển các chương trình tên lửa và thám hiểm Mặt Trăng để cạnh tranh với Liên Xô.
Đoạn 11-13: Sự qua đời đột ngột của Korolev và bước thụt lùi của Liên Xô.
Tổng hợp các ý trên, ta có ý chính của toàn bài là: “Cuộc chạy đua chinh phục Mặt Trăng giữa Liên Xô và Mỹ”.
Câu 27:
Tên lửa V2 là sản phẩm của quốc gia nào?
Đáp án C
Thông tin tại dòng 3-5: “Công nghệ tên lửa vũ trụ hiện đại được khởi nguồn từ Viện Ngiên cứu quân sự của Đức Quốc Xã...”
Câu 28:
Kiến trúc sư trưởng của chương trình tên lửa Liên Xô là ai?
Đáp án B
Thông tin tại dòng 20-21: “Sergei Pavlivich Korolev có một thời gian dài ở Đông Đức để nghiên cứu các tài liệu về V2, nhờ đó ông đã phát triển tên lửa R1 của Liên Xô...”
Câu 29:
Cụm từ “tên lửa liên lục địa” được dùng để chỉ:
Đáp án D
Tên lửa liên lục địa là loại tên lửa có tầm bắn xa, có thể bay xuyên từ lục địa này qua lục địa khác.
Câu 30:
Quốc gia nào sau đây có tàu vũ trụ đầu tiên hạ cánh xuống Mặt Trăng?
Đáp án B
Thông tin tại dòng 25-26: “Luna 2” thực hiện chuyến hạ cánh cứng đầu tiên lên mặt trăng vào năm 1959”.
Câu 31:
Kể từ khi tuyên bố tham vọng chinh phục Mặt Trăng, Mỹ mất bao lâu để thực hiện mục tiêu này?
Đáp án C
Thông tin tại dòng 32-33: “25.05.1961 Tổng thống Kennedy tuyên bố mục tiêu...” Thông tin tại dong 1-2: “Ngày 20.07.1969 Neil Armstrong đặt chân lên Mặt Trăng...” → Thời gian Mỹ thực hiện mục tiêu là 9 năm.
Câu 32:
Tên lửa nào sau đây do Wernher von Braun phát triển?
Đáp án C
Thông tin tại dòng 42-43: “Von Braun có nhiệm vụ phát triển tên lửa Saturn V với chiều cao 111 mét, cho đến nay vẫn là loại tên lửa đẩy lớn nhất thế giới”.
Câu 33:
Đáp án B
Ý chính trong hai câu văn nằm ở câu thứ hai “Nhưng, may mắn chỉ đến với những người thực sự tài năng và có quyết tâm”. Ở đây, tác giả muốn nhấn mạnh may mắn chỉ đến với người có tài năng và quyết tâm, do đó von Braun phải là một người có tài năng xuất chúng.
Câu 34:
Ý chính của đoạn 11 (dòng 49-55) là:
Đáp án D
Đoạn 11 mô tả các hoạt động của Liên Xô trong bối cảnh nước Mỹ dồn sức đầu tư cho chương trình Apollo: Thiết kế tài Sojus, chế tạo tên lửa N1, Korolev qua đời đột ngột. Do đó ý chính của đoạn là: “Diễn biến chương trình Mặt Trăng của Liên Xô.
Câu 35:
Dựa vào thông tin trong đoạn trích, tác giả nhiều khả năng sẽ đồng tình với nhận định nào sau đây?
Đáp án A
A. Năm 1966 là năm bước ngoặt trong cuộc cạnh tranh chinh phục Mặt Trăng
=> Đúng, năm 1966 Kovolev đột ngột qua đời, tác giả cho rằng “Nếu như Korolev không phải rời khỏi cuộc đua vì bệnh tật và cái chết, điều gì sẽ xảy ra?
B. Chương trình Mặt Trăng của Liên Xô thất bại mà không thu được thành tựu gì. => Sai, một thành tựu được nhắc tới trong bài viết chế tạo thành công tàu vũ trụ Sojus,vẫn còn hoạt động cho tới ngày nay.
C. Wernher von Braun là nhà khoa học tên lửa xuất chúng, không có đối thử
=> Sai, thông tin tại dòng 56: “Hai kỳ phùng địch thủ Kovolev và von Braun đã chỉ còn lại một hai.
D. Chương trình hàng không vũ trụ Liên Xô không phải đối thủ cạnh tranh của Mỹ. => Sai, thông tin tại dòng 34-35: “Đây là một dự án đầy tham vọng và vô cùng tốn kém nhưng được khích lệ bởi quyết tâm không để thua Liên Xô một lần nữa.
Câu 36:
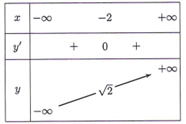
Đáp án C
Ta có suy ra
Từ bảng biến thiên, ta có
Vậy ba số a, b, c dương.
Câu 37:
Cho hàm số y = f(x) có bảng biến thiên như hình bên dưới. Đồ thị hàm số có tất cả bao nhiêu tiệm cận đứng và ngang?
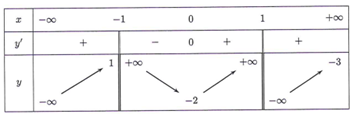
Đáp án B
Từ bảng biến thiên của hàm số y = f(x) ta có: và
+) . Suy ra đường tiệm cận ngang của đồ thị là y = 0
+) . Suy ra đường tiệm cận ngang của đồ thị là y = 2
Do đó đồ thị có hai tiệm cận đứng.
Vậy đồ thị hàm số có 4 tiệm cận.
Câu 38:
Cho hàm số y = f(x) liên tục trên R, có bảng biến thiên như hình vẽ bên. Đặt . Tìm tất cả các giá trị thực của m để hàm số có đúng 3 điểm cực trị.
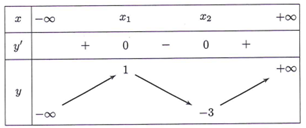
Đáp án C
Nhận xét: Số điểm cực trị của hàm số bằng số điểm cực trị của hàm số
Ta có bảng biến thiên của hàm số như sau:
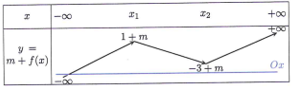
Hàm số có đúng 3 điểm cực trị
Câu 39:
Ông An muốn xây một bể chứa nước dạng hình hộp chữ nhật, phần nắp trên ông để trống một ô có diện tích bằng 20% diện tích của đáy bể. Biết đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng, bể có thể tích tối đa 10m3 nước và giá tiền thuê nhân công 500 000 đồng/m3. Số tiền ít nhất mà ông phải trả cho nhân công gần nhất với đáp án nào dưới đây?
Đáp án A
Gọi chiều rộng của đáy bể là a (a > 0) thì chiều dài của đáy bể là 2a; chiều cao của bể là h (h > 0). Thể tích của bể là
Diện tích toàn phần của bể là
Vậy tiền trả cho nhân công gần bằng 28.500 000 = 14 000 000 đồng.
Câu 40:
Đáp án A
Gọi t là thời gian tối thiểu để máy tính đạt được không dưới 95% dung lượng pin tối đa, hay
Câu 41:
Đầu mỗi tháng ông Bình đến gửi tiết kiệm vào ngân hàng số tiền là 20.000.000 đồng với lãi suất r%/tháng. Sau 2 tháng gửi, gia đình ông có việc đột xuất nên cần rút tiền về. Số tiền ông rút được cả vốn lẫn lãi là 40.300.500 đồng. Tính lãi suất hàng tháng mà ngân hàng áp dụng cho tiền gửi của ông Bình.
Đáp án A
Gọi số tiền ông Bình gửi vào đầu mỗi tháng là A. Ta có A = 20 000 000 đồng.
Theo đề bài, lãi suất là r/ tháng (r>0)
Gọi số tiền ông nhận được cả vốn lẫn lãi sau n tháng là ![]() .
.
+ Cuối tháng thứ nhất, khi ngân hàng đã tính lãi thì số tiền có được là:
+ Đầu tháng thứ hai, khi đã gửi thêm số tiền A đồng thì số tiền lúc đó là:
+ Cuối tháng thứ hai, khi ngân hàng đã tính lãi thì số tiền ông Bình có được là:
Theo giả thiết ta có:
Kết hợp điều kiện r > 0 ta được r = 0,005 =0,5%.
Câu 42:
Cho phương trình . Gọi S là tập hợp giá trị m nguyên với để phương trình có đúng 2 nghiệm. Tổng giá trị các phần tử của S bằng
Đáp án C
Điều kiện
Ta có
+)
+)
Xét 3 trường hợp:
Trường hợp 1: điều kiện của phương trình là x > 0, phương trình (1) có 2 nghiệm là x = 2 và x = 4.
Trường hợp 2: điều kiện của phương trình là x > 0
Khi đó, phương trình có 1 nghiệm là nên phương trình (1) có 2 nghiệm là x = 2 và x = 4
Trường hợp 3: m > 1 từ
Nên phương trình (1) có 2 nghiệm phân biệt
Khi đó phương trình đã cho có 2 nghiệm là x = lnm và x = 4
Suy ra, các giá trị m để phương trình có 2 nghiệm là và
Do đó các giá trị nguyên thỏa mãn yêu cầu bài toán là
Vậy tổng các phần tử của S là – 27.
Câu 43:
Tập nghiệm của bất phương trình là . Khi đó a - 2b + c bằng
Đáp án A
Ta có
Xét hàm số
Vì f''(x) > 0 nên f'(x) đồng biến trên và nên f'(x) = 0 có nghiệm duy nhất là do đó phương trình f(x) = 0 có tối đa là 2 nghiệm, nhận thấy . Ta có bảng biến thiên
![Tập nghiệm của bất phương trình 9^x - 2(x + 5)3^x + 9(2x + 10 > = 0 là S = [a; b] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/blobid4-1651907377.png)
Dựa vào bảng biến thiên của ta được
+)
+)
Từ đó ta được
Tập nghiệm của bất phương trình ban đầu là
Vậy a - 2b + c = 0
Câu 44:
Một thiết bị kỹ thuật là một khối tròn xoay. Mặt cắt của khối tròn xoay đó qua trục của nó được mô tả trong hình bên. Thể tích của thiết bị đó bằng
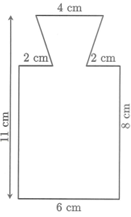
Đáp án D
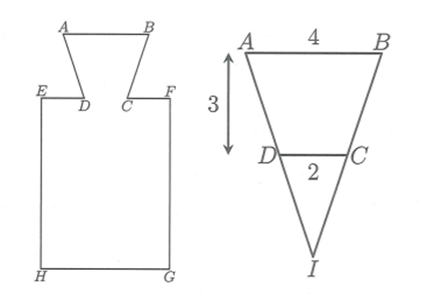
Chia khối tròn xoay được sinh bởi hình trên thành hai khối tròn xoay.
+) Khối nón cụt được sinh bởi hình thang ABCD.
+) Khối trụ được sinh bởi hình chữ nhật EFGH.
Gọi Vì nên CD là đường trung bình của tam giác IAB.
Thể tích khối nón cụt sinh bởi hình thang ABCD là:
Thể tích khối trụ sinh bởi hình chữ nhật EFGH là:
Vậy thể tích của thiết bị đó là:
Câu 45:
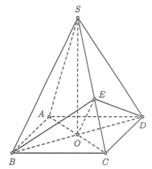
Cho hình chóp S.ABCD có ABCD là hình chữ nhật tâm I cạnh AB = 3a; BC = 4a. Hình chiếu của S trên mặt phẳng (ABCD) là trung điểm của ID. Biết rằng SB tạo với mặt phẳng (ABCD) một góc 45o. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD
Đáp án B
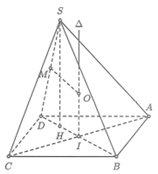
Gọi H là trung điểm của
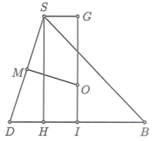
Trong mặt phẳng (SBD), qua I dựng đường thẳng song song với SH. Suy ra ![]() là trục đường tròn ngoại tiếp ABCD. Gọi M là trung điểm của SD.
là trục đường tròn ngoại tiếp ABCD. Gọi M là trung điểm của SD.
Trong mặt phẳng (SBD), dựng đường trung trực của đoạn thẳng SD, cắt ![]() tại O. Suy ra SO = OD.
tại O. Suy ra SO = OD.
Mà OA = OB = OC = OD nên O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có ABCD là hình chữ nhật tâm I cạnh AB = 3a; BC = 4a. và H là trung điểm DI.
Nên suy ra .
Ta có
Xét tam giác SHB vuông ại H có
Từ S dựng đường thẳng song song với BD, cắt tại G.
=> SHIG là hình chữ nhật
Đặt OI = x. Ta có:
Lại có:
Mà
Từ (1) và (2) =>
Vậy bán kính mặt cầu ngoại tiếp hình chóp là
Suy ra diện tích mặt cầu cần tính là
Câu 46:
Cho hình chóp S.ABC có Hình chiếu của đỉnh S là một điểm H nằm trong tam giác ABC. Biết khoảng cách giữa các cặp đường thẳng chéo nhau của hình chóp là Tính thể tích khối chóp S.ABC.
Đáp án D
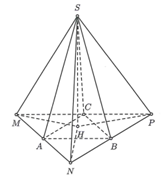
Gọi M, N, P là các điểm thỏa mãn A, B, C lần lượt là trung điểm của MN, NP, PM.
Ta có
Mà
Ta có
Dễ thấy
Gọi
Ta có
Mặt khác ta có
Tương tự ta có
Ta có
Vậy
Câu 47:
Cho hàm số f(x) có đạo hàm liên tục trên , thỏa mãn với mọi và . Mệnh đề nào dưới đây đúng?
Đáp án A
Xét . Chia 2 vế của phương trình cho ta được
Vì nên ta được suy ra
Vậy
Câu 48:

Đáp án B
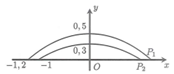
Gọi đường cong tương ứng với vành trên và vành dưới của máng lần lượt là (P1) và (P2)
Xét hệ trục tọa độ Oxy như hình vẽ
Khi đó parabol (P1) và (P2) đều có dạng
(P1) đi qua các điểm có tọa độ
(P2) đi qua các điểm có tọa độ
Suy ra và
Diện tích mặt cắt của máng parabol là
Vậy thể tích của khối silic làm 90 mặt máng là
Câu 49:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu và cắt nhau theo giao tuyến là đường tròn (C). Tìm tọa độ tâm J của đường tròn (C)
Đáp án B
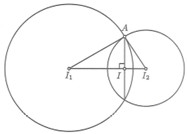
Ta có (S1) và (S2) có tâm và bán kính lần lượt là và
Gọi I(x; y; z) là tâm của đường tròn giao tuyến (C) và A là một điểm thuộc (C).
Câu 50:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC vuông tại C, đường thẳng AB có phương trình đường thẳng AC nằm trên mặt phẳng Biết B là điểm có hoành độ dương. Gọi (a; b; c) là tọa độ điểm C, giá trị của a + b + c bằng
Đáp án C
Ta có A là giao điểm của đường thẳng AB với mặt phẳng Tọa độ điểm A là nghiệm của hệ . Vậy điểm A(1; 2; 0)
Điểm B nằm trên đường thẳng AB nên điểm B có tọa độ
Theo giả thiết thì
Do , ta có nên B(2; 3; -4)
Theo giả thiết thì
Ta có
.
Vậy nên a + b + c =4
Câu 51:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; -2; -1), B(-2, -4, 3), C(1: 3: -1) và mặt phẳng . Biết điểm thỏa mãn đạt giá trị nhỏ nhất. Tính S = a + b + c
Đáp án C
Ta có
Do đó đạt giá trị nhỏ nhất bằng
Câu 52:
Cho số phức z, biết rằng các điểm biểu diễn hình học của các số phức z, iz và z+iz và tạo thành một tam giác có diện tích bằng 18. Môđun của số phức z bằng
Đáp án C
Gọi nên
Ta gọi lần lượt là các điểm biểu diễn các số phức z; iz và
Ta có
Câu 53:
Cho số phức với . Gọi (P) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng
Đáp án A
Gọi là điểm biểu diễn số phức z. Từ đó ta có:
Vậy (P) là một parabol có phương trình
Hoành độ giao điểm của (P) và trục hoành là nghiệm của phương trình:
Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng:
Câu 54:
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân, . Tính khoảng cách giữa hai đường thẳng chéo nhau AB', BC'
Đáp án B
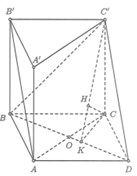
Gọi điểm D sao cho ABCD là hình bình hành và O là giao điểm
của AC và BD. Ta có nên .
Suy ra
Trong (ABCD), kẻ CK vuông góc BD tại K; trong (KCC’), kẻ CH vuông góc C’K tại H.
Khi đó CH vuông góc mp(BDC’) nên
Trong tam giá COD vuông tại C có:
là đường cao nên
Trong tam giác CC'K vuông tại C có CC' = AA' = ,
CH là đường cao nên
Vậy
Câu 55:
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng , cạnh bên SA = 2a. Côsin của góc giữa hai mặt phẳng (SDC) và (SAC) bằng
Đáp án C
Vì nên là hình chiếu vuông góc của
Gọi là góc giữa hai mặt phẳng (SAC) và (SDC). Suy ra:
Câu 56:
Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm trên khoảng .
Đáp án C
Ta có:
Nhận thấy phương trình không có nghiệm trên khoảng
Do đó yêu cầu bài toán có hai nghiệm thuộc khoảng
Vậy giá trị cần tìm là:
Câu 57:
Một đoàn tàu gồm 12 toa chở khách. Có 7 hành khách chuẩn bị lên tàu. Tính xác suất để đúng 3 toa có người.
Đáp án D
Số cách sắp xếp 7 người lên đoàn tàu 12 toa tàu là: 127. Suy ra:
Để có đúng có 3 toa có người thì ta phải sắp xếp như sau:
+) Chọn 3 toa trong 12 toa có:
+ Sắp xếp 7 hành khách vào 3 toa sao cho toa nào cũng có người thì có:
Suy ra số cách sắp xếp để có đúng có 3 toa có người là:
Xác suất để đúng 3 toa có người là:
Câu 58:
Trong mặt phẳng tọa độ Oxy, cho hình vuông MNPQ với M(10; 10), N(-10;10), P(-10; -10), Q(10; -10). Gọi S là tập hợp tất cả các điểm có tọa độ đều là các số nguyên nằm trong hình vuông MNPQ. Chọn ngẫu nhiên một điểm , khi đó xác xuất để chọn được điểm A thỏa mãn là
Đáp án A
Điểm A(x; y) nằm trong hình vuông MNPQ
Có 21 cách chọn x, 21 cách chọn y. Do đó số phần tử của không gian mẫu tập hợp các điểm thuộc S là n(S) = 21x21
Gọi Q là biến cố “Các điểm thỏa mãn ”.
Ta có
Khi đó
với Suy ra có 21 điểm thỏa mãn điều kiện trên nên số phần tử của biến cố Q là n(Q) = 21
Xác suất của biến cố Q là
Câu 59:
Tam giác ABC có ba góc A, B, C theo thứ tự lập thành cấp số cộng và C = 5A. Xác định số đo các góc A, B, C.
Đáp án B
Câu 60:
Đáp án A
Gọi ba số đó là x, y, z. Do ba số là các số hạng thứ 1, thứ 5 và thứ 25 của một cấp số cộng nên ta có:
Theo giả thiết, ta có:
Mặt khác, do x, y, z là các số hạng liên tiếp của một cấp số nhân nên.
Với d = 0 ta có: . Suy ra
Với x - d = 0, ta có: Suy ra ![]()
Theo đề bài ta có
Vậy n = 20
Do đó, phải lấy 20 số hạng đầu của cấp số cộng này để tổng của chúng bằng 1890.
Câu 61:
Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S) có phương trình . Viết phương trình mặt phẳng (Q) chứa trục hoành và tiếp xúc với mặt cầu (S).
Mặt cầu (S) có tâm I(1; 2; -1) và bán kính R = 1.
Gọi vectơ pháp tuyến của mặt phẳng (Q) là với
Vì mặt phẳng (Q) chứa trục hoành nên
=> Phương trình mặt phẳng
Ta có mặt phẳng (Q) tiếp xúc mặt cầu (S) nên
Với 3B - 4C = 0, chọn B = 4 => C = 3 phương trình mặt phẳng (Q) 4y + 3z = 0
Với B = 0 ta có phương trình mặt phẳng (Q): Cz = 0 <=> z = 0
Vậy có hai mặt phẳng thỏa mãn yêu cầu bài toán là
Câu 62:
Xét các số phức z thỏa mãn là số thực. Tập hợp các điểm biểu diễn của số phức 2z là một parabol (P). Tính diện tích hình phẳng giới hạn bởi (P)và trục hoành.
Giả sử
Khi đó
Ta có là số thực
Số phức 2z có điểm biểu diễn Quỹ tích các điểm M là parabol có phương trình
Xét phương trình hoành độ giao điểm của (P) và trục hoành, ta có
Vậy diện tích hình phẳng giới hạn bởi (P) và trục hoành là
