Đề thi Cuối học kỳ 2 Toán 6 có đáp án (Đề 2)
-
534 lượt thi
-
14 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
PHẦN I. TRẮC NGHIỆM
Hướng dẫn giải:
Đáp án đúng là: D
Số nghịch đảo của phân số –0,4 là \(\frac{1}{{ - 0,4}} = - \frac{1}{{0,4}}\).
Câu 2:
Hướng dẫn giải:
Đáp án đúng là: D
Đổi 0,25 m2 = 25 dm2.
Khi đó tỉ số phần trăm của 18 dm2 và 25 dm2 là: \(\frac{{18}}{{25}}.100\% = 72\% \)
Vậy tỉ số phần trăm của 18 dm2 và 0,25 m2 là: 72%.
Câu 3:
Hướng dẫn giải:
Đáp án đúng là: C
Độ dài mỗi đoạn dây là: 30 : 8 = 3,75 (cm).
Vì số 3,75 có chữ số thập phân thứ hai là 5 = 5 nên khi làm tròn đến chữ số thập phân thứ nhất ta được 3,75 ≈ 3,8.
Câu 4:
Giá niêm yết của một hộp sữa là 840 000 đồng. Trong chương trình khuyến mãi, mặt hàng này được giảm giá 15%. Như vậy khi mua một hộp sữa khuyến mãi thì người mua cần phải trả số tiền là:
Hướng dẫn giải:
Đáp án đúng là: B
Hộp sữa giảm 15% nên số tiền được giảm khi mua một hộp sữa là:
840 000 . 15% = 126 000 (đồng).
Người mua một hộp sữa khuyến mãi cần phải trả số tiền là:
840 000 – 126 000 = 714 000 (đồng).
Vậy người mua cần phải trả số tiền là 714 000 đồng khi mua một hộp sữa với giá khuyến mãi.
Câu 5:
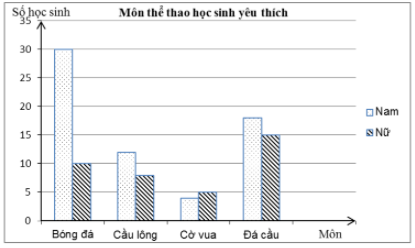
Môn thể thao nào có nhiều học sinh nữ thích chơi nhất?
Hướng dẫn giải:
Đáp án đúng là: D
Quan sát biểu đồ cột kép ta thấy môn thể thao có nhiều học sinh nữ thích chơi nhất là đá cầu.
Câu 6:
Hướng dẫn giải:
Đáp án đúng là: A
Tổng số lần thực hiện hoạt động bắn mũi tên là 20, số lần bắn trúng vào mục tiêu là 18 lần.
Do đó số lần không bắn trúng là 20 – 18 = 2 lần.
Xác suất thực nghiệm không bắn trúng bia là: \(\frac{2}{{20}} = \frac{1}{{10}}.\)
Câu 7:
Hướng dẫn giải:
Đáp án đúng là: B
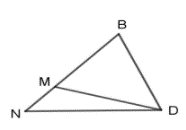
Các góc nhận tia DB làm cạnh là: \(\widehat {BDM};\widehat {BDN}\).
Câu 8:
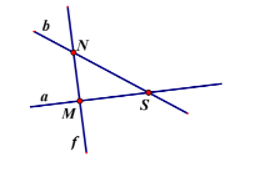
Hướng dẫn giải:
Đáp án đúng là: B
Đường thẳng a chứa các điểm M và S.
Câu 9:
PHẦN II. TỰ LUẬN
Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(5\frac{1}{3} - 2\frac{1}{3}\);
b) (–4,44 + 60 – 5,56) : (1,2 – 0,8);
c) \(1\frac{{13}}{{15}}.0,75 - \left( {\frac{8}{{15}} + 25\% } \right)\)
Hướng dẫn giải:
a) \(5\frac{1}{3} - 2\frac{1}{3}\)
\( = \left( {5 + \frac{1}{3}} \right) - \left( {2 + \frac{1}{3}} \right)\)
\( = 5 + \frac{1}{3} - 2 - \frac{1}{3}\)
\( = \left( {5 - 2} \right) + \left( {\frac{1}{3} - \frac{1}{3}} \right)\)
= 3
b) (–4,44 + 60 – 5,56) : (1,2 – 0,8)
= [60 + (– 4,44 – 5,56)] : 0,4
= [60 + (–10)] : 0,4
= 50 : 0,4
= 125.
c) \(1\frac{{13}}{{15}}.0,75 - \left( {\frac{8}{{15}} + 25\% } \right)\)
\( = \frac{{28}}{{15}}.\frac{{75}}{{100}} - \left( {\frac{8}{{15}} + \frac{{25}}{{100}}} \right)\)
\[ = \frac{{4.7}}{{3.5}}.\frac{{3.25}}{{4.25}} - \left( {\frac{8}{{15}} + \frac{1}{4}} \right)\]
\( = \frac{7}{5} - \frac{8}{{15}} - \frac{1}{4}\)
\( = \frac{{84}}{{60}} - \frac{{32}}{{60}} - \frac{{15}}{{60}}\)
\( = \frac{{37}}{{60}}\)
Câu 10:
a) \(\frac{2}{3}.x + \frac{1}{2} = \frac{1}{{10}}\);
b) \[\left( {4\frac{1}{2} - 2x} \right).1\frac{4}{{61}} = 6\frac{1}{2}\]
c) x – 83%.x = –1,7.
Hướng dẫn giải:
a) \(\frac{2}{3}.x + \frac{1}{2} = \frac{1}{{10}}\)
\(\frac{2}{3}.x = \frac{1}{{10}} - \frac{1}{2}\)
\(\frac{2}{3}.x = \frac{1}{{10}} - \frac{5}{{10}}\)
\(\frac{2}{3}.x = \frac{{ - 4}}{{10}}\)
\(\frac{2}{3}.x = \frac{{ - 2}}{5}\)
\(x = \frac{{ - 2}}{5}:\frac{2}{3}\)
\(x = \frac{{ - 2}}{5}.\frac{3}{2}\)
\(x = \frac{{ - 3}}{5}\)
Vậy \(x = \frac{{ - 3}}{5}\)
b) \[\left( {4\frac{1}{2} - 2x} \right).1\frac{4}{{61}} = 6\frac{1}{2}\].
\[\left( {\frac{9}{2} - 2x} \right).\frac{{65}}{{61}} = \frac{{13}}{2}\]
\[\frac{9}{2} - 2x = \frac{{13}}{2}:\frac{{65}}{{61}}\]
\[\frac{9}{2} - 2x = \frac{{13}}{2}.\frac{{61}}{{65}}\]
\[\frac{9}{2} - 2x = \frac{{13}}{2}.\frac{{61}}{{5.13}}\]
\[\frac{9}{2} - 2x = \frac{{61}}{{10}}\]
\[2x = \frac{9}{2} - \frac{{61}}{{10}}\]
\[2x = \frac{{45}}{{10}} - \frac{{61}}{{10}}\]
\[2x = \frac{{ - 16}}{{10}}\]
\[2x = \frac{{ - 8}}{5}\]
\[x = \frac{{ - 8}}{5}:2\]
\[x = \frac{{ - 8}}{5}.\frac{1}{2}\]
\[x = \frac{{ - 4}}{5}\]
Vậy \[x = \frac{{ - 4}}{5}\].
c) x – 83%.x = –1,7
\(x - \frac{{83}}{{100}}.x = - \frac{{17}}{{10}}\)
\(x.\left( {1 - \frac{{83}}{{100}}} \right) = - \frac{{17}}{{10}}\)
\(x.\frac{{100 - 83}}{{100}} = - \frac{{17}}{{10}}\)
\(x.\frac{{17}}{{100}} = \frac{{ - 17}}{{10}}\)
\(x = \frac{{ - 17}}{{10}}:\frac{{17}}{{100}}\)
\(x = \frac{{ - 17}}{{10}}.\frac{{100}}{{17}}\)
x = 10.
Vậy x = 10.
Câu 11:
Ban tổ chức dự định bán vé trận bóng đã có sự tham gia của đội tuyển Việt Nam tại sân vận động Mỹ Đình trong ba ngày. Ngày thứ nhất bán được \(\frac{3}{5}\) tổng số vé, ngày thứ hai bán được 25% tổng số vé. Số vé còn lại được bán trong ngày thứ ba.
a) Tính tổng số vé đã bán, biết 20% tổng số vé đã bán là 8000 vé.
b) Số vé được bán trong ngày thứ nhất là bao nhiêu?
c) Hỏi số vé đã bán trong ngày thứ ba bằng bao nhiêu phần trăm so với tổng số vé đã bán.
Hướng dẫn giải:
a) Tổng số vé được bán là: 8 000 : 20% = 40 000 (vé)
b) Số vé được bán trong ngày thứ nhất là: \(\frac{3}{5}.40\;000 = 24\;000\) (vé)
c) Số vé được bán trong ngày thứ hai là: 40 000 . 25% = 10 000 (vé)
Số vé được bán trong ngày thứ ba là: 40 000 – 24 000 – 10 000 = 6 000 (vé)
Số vé đã bán trong ngày thứ ba chiếm số phần trăm so với tổng số vé đã bán là:
\(\frac{{6\;000}}{{40\;000}}.100\% = 15\% \)
Câu 12:
Tổng hợp kết quả xét nghiệm Covid – 19 ở một phòng khám trong một tháng ta được bảng sau:
|
Tuần |
Số ca xét nghiệm |
Số ca dương tính |
|
1 |
210 |
115 |
|
2 |
205 |
128 |
|
3 |
232 |
130 |
|
4 |
189 |
176 |
a) Tuần nào có số kết quả xét nghiệm dương tính nhiều nhất? Cả tháng có bao nhiêu kết quả xét nghiệm là dương tính, âm tính?
b) Hãy tính và so sánh xác suất của thực nghiệm của các sự kiện một ca xét nghiệm có kết quả dương tính của tuần nhiều ca dương tính nhất và cả tháng (làm tròn kết quả đến hàng phần trăm).
Hướng dẫn giải:
a) Tuần 4 có kết quả xét nghiệm dương tính nhiều nhất (176 ca).
Số ca xét nghiệm có kết quả dương tính trong tháng đó là:
115 + 128 + 130 + 176 = 549 (ca).
Tổng số người đến phòng khám xét nghiệm trong tháng đó là:
210 + 205 + 232 + 189 = 836 (ca)
Số ca xét nghiệm có kết quả âm tính trong tháng đó là:
836 – 549 = 287 (ca)
b) Số ca xét nghiệm dương tính trong tuần 4 là 176 ca.
Xác suất của thực nghiệm theo số ca dương tính trong tuần 4 là:
\(\frac{{176}}{{189}} = 0,931216931...\) ≈ 0,93 (làm tròn kết quả đến hàng phần trăm).
Xác suất của thực nghiệm theo số ca dương tính trong cả tháng là:
\(\frac{{549}}{{836}} = 0,656698564...\) ≈ 0,66 (làm tròn kết quả đến hàng phần trăm).
Do đó 0,66 < 0,93.
Vậy xác suất xét nghiệm có kết quả dương tính ở tuần 4 lớn hơn so với cả tháng.
Câu 13:
Vẽ tia Ax.
a) Vẽ góc xAy có số đo bằng 70°, góc xAy là góc gì?
b) Trên tia Ax lấy điểm B và C sao cho B nằm giữa A và C, AB = 3 cm, AC = 5 cm. Gọi M là trung điểm của AB. Tính độ dài đoạn thẳng BC và MC.
Hướng dẫn giải:
a) Góc xAy có số đo bằng 70° < 90° nên là góc nhọn.
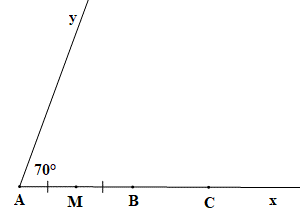
b) Điểm B nằm giữa điểm A và C nên AB + BC = AC
Hay 3 + BC = 5
Suy ra BC = 5 – 3 = 2 cm.
Vì M là trung điểm của AB nên M nằm giữa A và B do đó AM + MB = AB.
Mà M là trung điểm của AB nên AM = MB
Do đó AM + AM = AB
Suy ra 2AM = AB
\(AM = \frac{{AB}}{2}\)
\(AM = \frac{3}{2} = 1,5\) cm
Vì M nằm giữa A và B ; B nằm giữa A và C nên M nằm giữa A và C.
Do đó AM + MC = AC
Suy ra MC = AC – AM
MC = 5 – 1,5 = 3,5 cm.
Câu 14:
Hướng dẫn giải:
\[A = \frac{{10}}{{3.7}} - \frac{5}{{7.12}} - \frac{7}{{12.19}} - \frac{5}{{19.24}}\]
\(A = \frac{{3 + 7}}{{3.7}} - \frac{{12 - 7}}{{7.12}} - \frac{{19 - 12}}{{12.19}} - \frac{{24 - 19}}{{19.24}}\)
\[A = \left( {\frac{3}{{3.7}} + \frac{7}{{3.7}}} \right) - \left( {\frac{{12}}{{7.12}} - \frac{7}{{7.12}}} \right) - \left( {\frac{{19}}{{12.19}} - \frac{{12}}{{12.19}}} \right) - \left( {\frac{{24}}{{19.24}} - \frac{{19}}{{19.24}}} \right)\]
\[A = \left( {\frac{1}{7} + \frac{1}{3}} \right) - \left( {\frac{1}{7} - \frac{1}{{12}}} \right) - \left( {\frac{1}{{12}} - \frac{1}{{19}}} \right) - \left( {\frac{1}{{19}} - \frac{1}{{24}}} \right)\]
\[A = \frac{1}{3} + \frac{1}{7} - \frac{1}{7} + \frac{1}{{12}} - \frac{1}{{12}} + \frac{1}{{19}} - \frac{1}{{19}} + \frac{1}{{24}}\]
\[A = \frac{1}{3} + \left( {\frac{1}{7} - \frac{1}{7}} \right) + \left( {\frac{1}{{12}} - \frac{1}{{12}}} \right) + \left( {\frac{1}{{19}} - \frac{1}{{19}}} \right) + \frac{1}{{24}}\]
\(A = \frac{1}{3} + \frac{1}{{24}}\)
\(A = \frac{8}{{24}} + \frac{1}{{24}}\)
\(A = \frac{9}{{24}}\)
\(A = \frac{3}{8}\)
Vậy \(A = \frac{3}{8}\)
