Phóng xạ
-
293 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Chất Iốt phóng xạ \[{}_{53}^{131}I\] dùng trong y tế có chu kỳ bán rã 8 ngày đêm. Nếu nhận được 100g chất này thì sau 8 tuần lễ còn bao nhiêu?
Trả lời:
t = 8 tuần = 56 ngày = 7.T .Suy ra sau thời gian t thì khối lượng chất phóng xạ \[{}_{53}^{131}I\] còn lại là :
\[m = {m_0}{.2^{ - \frac{t}{T}}} = {100.2^{ - 7}} = 0,78gam\]
Đáp án cần chọn là: B
Câu 2:
Một chất phóng xạ có chu kỳ bán rã là 3,8 ngày. Sau thời gian 11,4 ngày thì độ phóng xạ (hoạt độ phóng xạ) của lượng chất phóng xạ còn lại bằng bao nhiêu phần trăm so với độ phóng xạ của lượng chất phóng xạ ban đầu?
Trả lời:
T = 3,8 ngày ; t = 11,4 = 3T ngày. Do đó ta đưa về hàm mũ để giải nhanh như sau:
\[H = {H_0}{.2^{ - \frac{t}{T}}}\]
\[ \Leftrightarrow \frac{H}{{{H_0}}} = {2^{ - \frac{t}{T}}}\]
\[ \Leftrightarrow \frac{H}{{{H_0}}} = {2^{ - 3}} = \frac{1}{8} = 12,5\% \]
Đáp án cần chọn là: C
Câu 3:
\[{}^{22}Na\] phân rã với chu kì T = 2,6 năm. Khối lượng ban đầu là m0. Sau 2 năm lượng \[{}^{22}Na\] phân rã bao nhiêu %?
Trả lời:
t = 2 năm, T = 2,6 năm
Ta có: khối lượng hạt nhân đã phân rã:
\[\Delta m = {m_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)\]
\[ \to \frac{{\Delta m}}{{{m_0}}} = 1 - {2^{ - \frac{t}{T}}} = 1 - {2^{ - \frac{2}{{2,6}}}}\]
\[ \to \frac{{\Delta m}}{{{m_0}}} = 0,4133 = 41.33\% \]
Đáp án cần chọn là: A
Câu 4:
Tính số hạt nhân bị phân rã sau 1s trong 1g Rađi \[{}^{226}Ra\] . Cho biết chu kỳ bán rã của \[{}^{226}Ra\] là 1580 năm. Số Avôgađrô là NA = 6,02.1023 mol-1.
Trả lời:
Số hạt nhân nguyên tử có trong 1 gam 226Ra là :
\[{N_0} = \frac{m}{A}.{N_A} = \frac{1}{{226}}.6,{022.10^{23}} = 2,{6646.10^{21}}\]
Suy ra số hạt nhân nguyên tử Ra phân rã sau 1 s là :
\[\Delta N = {N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)\]
\[ \Rightarrow \Delta N = 2,{6646.10^{21}}\left( {1 - {2^{ - \frac{1}{{1580.365.86400}}}}} \right)\]
\[ \Rightarrow \Delta N = 3,{70.10^{10}}\]
Đáp án cần chọn là: D
Câu 5:
Pôlôni \[{}^{210}Po\] là một chất phóng xạ có chu kì bán rã 140 ngày đêm. Hạt nhân pôlôni phóng xạ sẽ biến thành hạt nhân chì (\[{}^{210}Po\]) và kèm theo một hạt a. Ban đầu có 42mg chất phóng xạ pôlôni. Khối lượng chì sinh ra sau 280 ngày đêm là:
Trả lời:
Ta có:
\[{m_{Pb}} = \frac{{\Delta {m_{Po}}}}{{{A_{Po}}}}.{A_{Pb}}\]
\[ = {m_0}\frac{{{A_{Pb}}}}{{{A_{Po}}}}\left( {1 - {2^{\frac{t}{T}}}} \right)\]
\[ = 42\frac{{206}}{{210}}\left( {1 - {2^{ - \frac{{208}}{{140}}}}} \right) = 30,9mg\]
Đáp án cần chọn là: A
Câu 6:
Đồng vị \[{}_{11}^{24}Na\]là chất phóng xạ β- tạo thành hạt nhân magiê( \[{}_{12}^{24}Mg\]). Ban đầu có 12gam Na và chu kì bán rã là 15 giờ. Sau 45 h thì khối lượng Mg tạo thành là :
Trả lời:
Nhận xét : t = 3T nên ta dùng hàm mũ 2 để giải cho nhanh bài toán :
- Khối lượng Na bị phân rã sau t = 45 giờ = 3T :
\[\Delta m = {m_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right) = 12\left( {1 - {2^{ - 3}}} \right)\]
\[ \leftrightarrow \Delta m = 10,5g\]
- Suy ra khối lượng của Mg tạo thành :
\[{m_{con}} = \frac{{\Delta {m_{me.}}{A_{con}}}}{{{A_{me}}}}\]
\[ \to {m_{con}} = \frac{{10,5}}{{24}}.24 = 10,5g\]
Đáp án cần chọn là: A
Câu 7:
Một lượng chất phóng xạ sau 12 năm thì còn lại 1/16 khối lượng ban đầu của nó. Chu kì bán rã của chất đó là
Trả lời:
Ta có
\[\frac{m}{{{m_0}}} = \frac{1}{{{2^{\frac{t}{T}}}}} = \frac{1}{{16}} = \frac{1}{{{2^4}}}\]
\[ \to \frac{t}{T}4\]
\[ \Rightarrow T = \frac{t}{4} = \frac{{12}}{4} = 3\] năm
Đáp án cần chọn là: A
Câu 8:
Hạt nhân A đang đứng yên thì phân rã thành hạt nhân B có khối lượng mB và hạt α có khối lượng mα. Tỉ số giữa động năng của hạt α và động năng của hạt nhân B ngay sau phân rã bằng:
Trả lời:
A phân rã => B + α
áp dụng định luật bảo toàn động lượng, ta có:
\[\overrightarrow {{P_t}} = \overrightarrow {{P_s}} \]
\[ \leftrightarrow 0 = {m_B}\overrightarrow {{v_B}} + {m_\alpha }\overrightarrow {{v_\alpha }} \]
\[ \to {m_B}\overrightarrow {{v_B}} = - {m_\alpha }\overrightarrow {{v_\alpha }} \]
Mặt khác, ta có:
\[{{\rm{W}}_d} = \frac{1}{2}m{v^2} = \frac{{{P^2}}}{{2m}}\]
\[ \to P_B^2 = P_\alpha ^2\]
\[ \leftrightarrow {\rm{2}}{{\rm{m}}_B}{{\rm{W}}_{{d_B}}} = 2{m_\alpha }{{\rm{W}}_{{d_\alpha }}}\]
\[\frac{{{{\rm{W}}_{{d_\alpha }}}}}{{{{\rm{W}}_{{d_B}}}}} = \frac{{{m_B}}}{{{m_\alpha }}}\]
Đáp án cần chọn là: B
Câu 9:
Hạt nhân A (có khối lượng mA) đứng yên phóng xạ thành hạt B (có khối lượng mB) và C (có khối lượng mC) theo phương trình A → B + C. Nếu phản ứng tỏa năng lượng ∆E thì động năng của B là:
Trả lời:
A phân rã =>B + C
\[\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{P_t}} = \overrightarrow {{P_s}} }\\{{m_A}{c^2} = \left( {{m_B} + {m_C}} \right){c^2} + {{\rm{W}}_{{d_B}}} + {{\rm{W}}_{{d_C}}}}\end{array}} \right.\]
\[ \leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 = {m_B}\overrightarrow {{v_B}} + {m_C}\overrightarrow {{v_C}} }\\{\Delta E = {{\rm{W}}_{{d_B}}} + {{\rm{W}}_{{d_C}}}}\end{array}} \right.\]
\[\left\{ {\begin{array}{*{20}{c}}{{{\rm{W}}_{{d_B}}} = \frac{{{m_C}}}{{{m_C} + {m_B}}}\Delta E}\\{{{\rm{W}}_{{d_C}}} = \frac{{{m_B}}}{{{m_C} + {m_B}}}\Delta E}\end{array}} \right.\]
Đáp án cần chọn là: B
Câu 10:
Một hạt nhân X, ban đầu đứng yên, phóng xạ α và biến thành hạt nhân Y. Biết hạt nhân X có số khối là A, hạt α phát ra tốc độ v. Lấy khối lượng của hạt nhân bằng số khối của nó tính theo đơn vị u. Tốc độ của hạt nhân Y bằng:
Trả lời:
\[{}_Z^AX \to {}_2^4\alpha + {}_{Z - 2}^{A - 4}Y\]
Áp dụng định luật bảo toàn động lượng, ta có:
\[0 = {m_Y}\overrightarrow {{v_Y}} + {m_\alpha }\overrightarrow {{v_\alpha }} \]
\[ \to {m_Y}\overrightarrow {{v_Y}} = - {m_\alpha }\overrightarrow {{v_\alpha }} \]
\[ \to {v_Y} = \frac{{{m_\alpha }{v_\alpha }}}{{{m_Y}}} = \frac{{4v}}{{A - 4}}\]
Đáp án cần chọn là: D
Câu 11:
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã T của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã ΔN và số hạt ban đầu N0. Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?
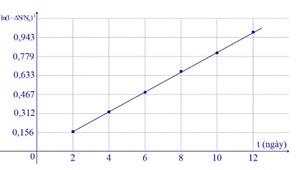
Trả lời:
Ta có: \[N = {N_0}{e^{ - \lambda t}}\]
→ Số hạt bị phân rã là:
\[\Delta N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}\left( {1 - {e^{ - \lambda t}}} \right)\]
\[ \Rightarrow \frac{{\Delta N}}{{{N_0}}} = 1 - {e^{ - \lambda t}}\]
\[ \Rightarrow 1 - \frac{{\Delta N}}{{{N_0}}} = {e^{ - \lambda t}}\]
\[ \Rightarrow \frac{1}{{\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)}} = {e^{\lambda t}}\]
\[ \Rightarrow \ln {\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\]
Từ đồ thị ta thấy: \[\lambda \approx 0,078\]
\[ \Rightarrow T = \frac{{\ln 2}}{\lambda } \approx 8,9\](ngày)
Đáp án cần chọn là: B
Câu 12:
Một chất phóng xạ có chu kì bán rã là 3,8 ngày. Số hạt nhân sẽ bị phân rã hết 70% sau thời gian là
Trả lời:
Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: N=N0.2−tTN=N0.2−tT
Số hạt nhân con được tạo thành hay số hạt nhân mẹ đã bị phân rã sau thời gian t được xác định bởi:
\[N' = {N_0} - N = {N_0}.\left( {1 - {2^{ - \frac{t}{T}}}} \right) = 70\% {N_0}\]\[ \Rightarrow \left( {1 - {2^{ - \frac{t}{T}}}} \right) = 70\% = 0,7\]
\[ \Rightarrow {2^{ - \frac{t}{T}}} = 0,3\]
\[ \Rightarrow t = - T.{\log _2}\left( {0,3} \right) = 1,74T = 1,74.3,8 = 6,6\]
Vậy thời gian là 6,6 ngày.
Đáp án cần chọn là: A
Câu 13:
Gọi N0 là số hạt nhân phóng xạ ban đầu (t = 0) và ΔN là số hạt nhân đã phóng xạ sau thời gian t. Đồ thị nào sau đây biểu thị sự biến thiên của ΔN theo thời gian?

Trả lời:
Số hạt đã bị phân rã được xác định theo công thức:
\[\Delta N = {N_0}.\left( {1 - {2^{ - \frac{t}{T}}}} \right)\]
Hàm số \[\Delta N = {N_0}.\left( {1 - {2^{ - \frac{t}{T}}}} \right)\] tăng từ 0 theo t và có tiệm cận ngang đi qua N0.
⇒ Đồ thị biểu diễn sự biến thiên của ΔN theo thời gian là đồ thị B.
Đáp án cần chọn là: B
Câu 14:
Các tế bào ung thư dễ bị tổn thương dưới tác dụng của tia X hoặc tia gamma hơn các tế bào khỏe mạnh. Mặc dù ngày nay đã có các máy gia tốc tuyến tính thay thế, nhưng trước kia nguồn tiêu chuẩn để điều trị là phóng xạ \[{}^{60}Co\]. Đồng vị này phân rã β thành \[{}^{60}Ni\] ở trạng thái kích thích, nhưng \[{}^{60}Ni\] ngay sau đó trở về trạng thái cơ bản và phát ra hai photon gamma, mỗi photon có năng lượng xấp xỉ 1,2 MeV. Biết rằng chu kì bán rã của phân rã β là 5,27 năm. Xác định số hạt nhân \[{}^{60}Co\] có mặt trong nguồn 6000 Ci thường được dùng trong các bệnh viện.
Trả lời:
Độ phóng xạ của hạt nhân \[{}^{60}Co\] là:
\[H = N\frac{{\ln }}{2} \Rightarrow N = \frac{{H.T}}{{\ln 2}}\]
\[ \Rightarrow N = \frac{{6000.3,{{7.10}^{10}}.5,27.365,25.86400}}{{\ln 2}} \approx 5,{33.10^{22}}\]
Đáp án cần chọn là: A
Câu 15:
Hạt nhân \[{}_{92}^{234}U\] đang đứng yên thì phân rã phóng xạ ra hạt α. Thực nghiệm đo được động năng của hạt α bằng 12,89 MeV. Sự sai lệch giữa giá trị tính toán và giá trị đo được đã giải thích bằng việc phát ra bức xạ γ cùng hay với hạt αα trong quá trình phân rã \[{}_{92}^{234}U\]. Khối lượng hạt nhân \[{}_{92}^{234}U,{}_{90}^{230}Th\] và hạt α lần lượt bằng 233,9904u: 229,9737u và 4,0015lu. Biết rằng hằng số Planck, vận tốc ánh sáng trong chân không và điện tích nguyên tố có giá trị lần lượt bằng 6,625.10-34J.s; 3.108m/svà 1,6.10-19C. Cho biết lu = 931,5 MeV/c2. Bước sóng của bức xạ γ phát ra là:
Trả lời:
Ta có:
\[ \Leftrightarrow \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{\lambda } = \frac{{229,9737u}}{{229,9737u + 4,00151u}}\]
\[.\left( {233,9904u - 229,9737u - 4,00151u} \right).{c^2} - 12,89MeV\]
\[ \Leftrightarrow \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{\lambda } = 0,983.0,01519u.{c^2} - 12,89MeV\]
\[ \Leftrightarrow \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{\lambda } = 0,983.0,01519.\frac{{931,5MeV}}{{{c^2}}}.{c^2} - 12,89MeV\]
\[ \Leftrightarrow \lambda = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{\left( {0,983.0,01519.931,5 - 12,89} \right){{.10}^6}.1,{{6.10}^{ - 19}}}}\]
\[ \Leftrightarrow \lambda = 1,{22.10^{ - 12}}\left( m \right)\]
Đáp án cần chọn là: C
Câu 16:
Một trong những phát hiện mang tính cách mạng của ngành khảo cổ học thế kỷ 20 là sự phát hiện ra lăng mộ của Pharaoh Ai Cập Tutankhanmun vào năm 1922 bởi Howard Carter. Cùng với xác ướp, nhiều vận dụng cũng được chuyển khỏi lăng mộ, trong đó bao gồm: (1) Các mảnh kính (2) Dao cạo bằng đồng (3) Trái cây khô (4) Giày da. Những vật nào trong số những vật trên có thể được dùng để xác định niên đại của lăng mộ cổ theo phương pháp đồng vị phóng xạ Carbon?
Trả lời:
Phương pháp đồng vị phóng xạ Carbon chỉ dùng đối với cổ vật có nguồn gốc sinh vật.
Vậy những vật có thể dùng là: Trái cây khô và giày da.
Đáp án cần chọn là: A
