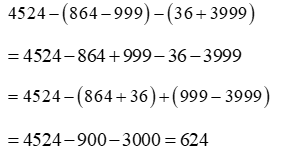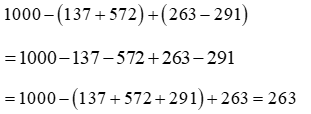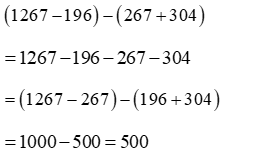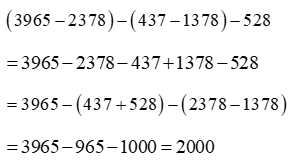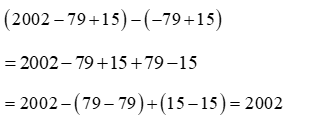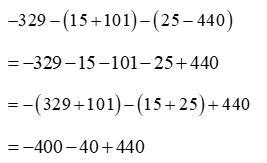Dạng 4. Quy tắc dấu ngoặc có đáp án
-
1470 lượt thi
-
32 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Vận dụng quy tắc dấu ngoặc và tính chất giao hoán, kết hợp ta có:
Câu 3:
Vận dụng quy tắc dấu ngoặc và tính chất giao hoán, kết hợp ta có:
Câu 4:
Vận dụng quy tắc dấu ngoặc và tính chất giao hoán, kết hợp ta có:
Câu 13:
\(\left( {1456 + 23} \right) - 1456 = \left( {1456 - 1456} \right) + 23 = 23.\)
Câu 14:
Câu 15:
\(\left( {116 + 124} \right) + \left( {215 - 116 - 124} \right) = \left( {116 - 116} \right) + \left( {124 - 124} \right) + 215 = 215\)
Câu 16:
\(\left( {435 - 167 - 89} \right) - \left( {435 - 89} \right) = \left( {435 - 435} \right) + \left( { - 89 + 89} \right) - 167 = - 167.\)
Câu 17:
\[\left( {a + b + c} \right) - \left( {a - b + c} \right) = a + b + c - a + b - c = 2b\]
Câu 18:
\[\left( {a + b - c} \right) + \left( {a - b} \right) - \left( {a - b - c} \right) = a + b - c + a - b - a + b + c = a + b\]
Câu 19:
\[ - \left( {a - b - c} \right) - \left( { - a + b + c} \right) - \left( {a - b + c} \right) = - a + b + c + a - b - c - a + b - c = - a + b - c\]
Câu 20:
Thu gọn các tổng sau:
\[\left( {a - b + c - d} \right) - \left( {a + b + c + d} \right)\]\(\left( {a - b + c - d} \right) - \left( {a + b + c + d} \right) = a - b + c - d - a - b - c - d = - 2b - 2d = - 2\left( {b + d} \right)\)
Câu 21:
\(\left( { - a + b - c} \right) + \left( {a - b} \right) - \left( {a - b + c} \right) = - a + b - c + a - b - a + b - c = - a + b - 2c\)
Câu 22:
\( - \left( {a - b - c} \right) + \left( {b - c + d} \right) - \left( { - a + b + d} \right) = - a + b + c + b - c + d + a - b - d = b.\)
Câu 23:
\[x + 8 - y = \left( { - 53} \right) + 8 - 45 = - 45 - 45 = - 90\]
Câu 24:
\[x + y + z - y = x + z = \left( { - 53} \right) + \left( { - 15} \right) = - 68\]
Câu 25:
\[16 + x - (y + z) - x = 16 - \left[ {45 + \left( { - 15} \right)} \right] = 16 - 30 = - 14\]
Câu 26:
Với a = -13, b = 25, c = -30. Ta có
\(a + a + 12 - b = 2a - b + 12 = 2.\left( { - 13} \right) - 25 + 12 = - 39\)
Câu 27:
Với a = -13, b = 25, c = -30. Ta có
\(a + b - \left( {c + b} \right) = a - c = - 13 + 30 = 17.\)
Câu 28:
Với a = -13, b = 25, c = -30. Ta có
\(25 + a - \left( {b + c} \right) - a = 25 - b - c = 25 - 25 + 30 = 30.\)
Câu 29:
\(382 + 531 - 282 - 331 = \left( {382 - 282} \right) + \left( {531 - 331} \right) = 100 + 200 = 300;\)
Câu 30:
)\(7 - 8 + 9 - 10 + 11 - 12 + ... + 2009 - 2010\)
\( = \left( {7 - 8} \right) + \left( {9 - 10} \right) + \left( {11 - 12} \right) + ... + \left( {2009 - 2010} \right)\)
\( = \underbrace {\left( { - 1} \right) + \left( { - 1} \right) + ... + \left( { - 1} \right)}_{gom{\rm{ }}\,1002\,{\rm{ }}so\,hang\, - 1} = - 1002\)
Câu 31:
\( - 1 - 2 - 3 - 4 - ... - 2008 - 2009 - 2010\)
\( = - \left( {1 + 2 + 3 + ... + 2008 + 2009 + 2010} \right) = \frac{{\left( {1 + 2010} \right).2010}}{2} = - 2021055\)
Câu 32:
\(1 - 3 - 5 + 7 - 9 - 11 + ... + 1000 - 1002 - 2004\)
\[ = \left( {1 - 3 - 5} \right) + \left( {7 - 9 - 11} \right) + ... + \left( {1000 - 1002 - 1004} \right)\] \[ = \underbrace {\left( { - 7} \right) + \left( { - 7} \right) + ... + \left( { - 7} \right)}_{gom\,334\,so\,hang\,} = - \left( {\underbrace {7 + 7 + ... + 7}_{gom\,334\,so\,hang}} \right) = - 7\,.\,334 = - 2338.\]

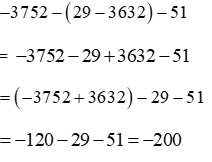
![Tính nhanh: 321 + {-15 + [30 + (-321)]} (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/09/blobid1-1664273528.png)