16 câu hỏi trắc nghiệm thuộc Đề thi Toán 6 Học kì 2 có đáp án (Đề 9)

Câu 1:

Một cửa hàng bán điện thoại lấy ý kiến đánh giá của khách hàng về thái độ phục vụ của nhân viên. Biểu đồ tranh dưới đây là kết quả đánh giá của khách hàng về thái độ phục vụ của nhân viên X trong một tuần (mỗi biểu tượng thể hiện kết quả một lần đánh giá, rất hài hài lòng: ♡, hài lòng J, không hài lòng L).

Thứ Hai	♡♡J
Thứ Ba	♡J
Thứ Tư	♡J♡♡
Thứ Năm	J♡♡L
Thứ Sáu	J♡L
Thứ Bảy	♡♡L♡

Có bao nhiêu lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên X trong tuần?

A. 11

B. 10

C. 9

D. 12

Xem đáp án

Đáp án đúng là: D

Số lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên X trong các ngày:

- Ngày thứ hai là: 2 lượt;

- Ngày thứ ba là: 1 lượt;

- Ngày thứ tư là: 3 lượt;

- Ngày thứ năm là: 2 lượt;

- Ngày thứ sáu là: 1 lượt;

- Ngày thứ bảy là: 3 lượt;

Số lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên X trong tuần là:

2 + 1 + 3 + 2 + 1 + 3 = 12 (lượt).

Vậy số lượt khách hàng rất hài lòng về thái độ phục vụ của nhân viên X trong tuần là 12 lượt.

Câu 2:

Hằng ngày Nam đều đi xe buýt đến trường. Nam ghi lại thời gian chờ xe của một số lần và được kết quả như bảng sau:

Thời gian chờ	Dưới 1 phút	Từ 1 phút đến 5 phút	Hơn 5 phút đến dưới 10 phút	Từ 10 phút trở lên
Số lần	3	8	7	2

Xác suất thực nghiệm của sự kiện “Nam chờ xe buýt với thời gian ít nhất” là:

A. 3%

B. 2%

C. 10%

D. 15%

Xem đáp án

Đáp án đúng là: D

Các kết quả về thời gian chờ có thể xảy ra khi Nam đi xe buýt đến trường bao gồm: dưới 1 phút; từ 1 đến 5 phút; hơn 5 phút đến dưới 10 phút; từ 10 phút trở lên;

Suy ra, sự kiện “Nam chờ xe buýt với thời gian ít nhất” có nghĩa là kết quả thời gian gian chờ xe buýt dưới 1 phút (3 lần);

Số lần Nam chờ xe buýt để đi đến trường là:

3 + 8 + 7 + 2 = 20 (lần)

Xác suất thực nghiệm của sự kiện “Nam chờ xe buýt với thời gian ít nhất” là:

$\frac{3}{20} = 0, 15 = 15 %$

Vậy xác suất thực nghiệm của sự kiện “Nam chờ xe buýt với thời gian ít nhất” là 15%.

Câu 3:

Giá trị của biểu thức A = 10 . (a – b) + a . b, với a = 1; b = 1,5 là:

A. – 3,5

B. 6,5

C. 3,5

D. – 6,5

Xem đáp án

Đáp án đúng là: A

Thay a = 1; b = 1,5 vào biểu thức A = 10. (a – b) + a.b, ta được:

A = 10. (1 – 1,5) + 1. 1,5 = 10. (– 0,5) + 1,5

= – 5 + 1,5 = – (5 – 1,5) = – 3,5.

Câu 4:

Trên hình vẽ bên, có bao nhiêu tia phân biệt gốc B?

A. 2

B. 3

C. 4

D. 5

Xem đáp án

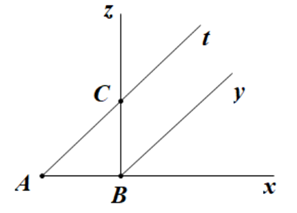
Đáp án đúng là: C

Quan sát hình vẽ, các tia phân biệt gốc B là: tia BA; tia Bz; tia By và tia Bx.

Vậy có 4 tia phân biệt gốc B.

Câu 5:

Thực hiện phép tính:

a) $3 \frac{1}{2} + \frac{1}{4} : \frac{5}{12} - 0, 5$ ;

Xem đáp án

$\begin{array}{l} a) 3 \frac{1}{2} + \frac{1}{4} : \frac{5}{12} - 0, 5 \\ = \frac{3.2 + 1}{2} + \frac{1}{4} . \frac{12}{5} - \frac{1}{2} \\ = \frac{7}{2} + \frac{3}{5} - \frac{1}{2} \\ = \frac{6}{2} + \frac{3}{5} \\ = 3 + \frac{3}{5} = 3 \frac{3}{5} \end{array}$

Câu 6:

b) $\frac{- 3}{10} . \frac{7}{15} + \frac{3}{10} . \frac{- 8}{15} - (- \frac{53}{10})$

Xem đáp án

$\begin{array}{l} b) \frac{- 3}{10} . \frac{7}{15} + \frac{3}{10} . \frac{- 8}{15} - (- \frac{53}{10}) \\ = \frac{- 3}{10} . \frac{7}{15} + \frac{- 3}{10} . \frac{8}{15} + \frac{53}{10} \\ = \frac{- 3}{10} . (\frac{7}{15} + \frac{8}{15}) + \frac{53}{10} \\ = \frac{- 3}{10} . \frac{15}{15} + \frac{53}{10} \\ = \frac{- 3}{10} + \frac{53}{10} \\ = \frac{53 - 3}{10} \\ = \frac{50}{10} \\ = 5 \end{array}$

Câu 7:

c) 200% + (4,02 + 5,24) – (14,02 – 4,76) – 1²⁰²².

Xem đáp án

c) 200% + (4,02 + 5,24) – (14,02 – 4,76) – 1²⁰²²

= 2 + 4,02 + 5,24 – 14,02 + 4,76 – 1

= (2 – 1) + (5,24 + 4,76) – (14, 02 – 4,02)

= 1 + 10 – 10 = 1.

Câu 8:

Tìm x biết:

a) $x - \frac{9}{15} = \frac{- 7}{5}$ ;

Xem đáp án

$\begin{array}{l} a) x - \frac{9}{15} = \frac{- 7}{5} \\ x - \frac{3}{5} = \frac{- 7}{5} \\ x = \frac{3}{5} - \frac{7}{5} \\ x = - (\frac{7}{5} - \frac{3}{5}) \\ x = \frac{- 4}{5} \\ Vậy x = \frac{- 4}{5} \end{array}$

Câu 9:

$b) \frac{1}{4} x + \frac{3}{8} (x - 2) = - \frac{11}{4}$

Xem đáp án

$\begin{array}{l} b) \frac{1}{4} x + \frac{3}{8} (x - 2) = - \frac{11}{4} \\ \frac{1}{4} x + \frac{3}{8} x - \frac{3}{8} .2 = - \frac{11}{4} \\ \frac{2}{8} x + \frac{3}{8} x - \frac{3}{4} = - \frac{11}{4} \\ \frac{5}{8} x = \frac{3}{4} - \frac{11}{4} \\ \frac{5}{8} x = - (\frac{11}{4} - \frac{3}{4}) \\ \frac{5}{8} x = - \frac{8}{4} \\ \frac{5}{8} x = - 2 \\ x = - 2 : \frac{5}{8} \\ x = - 2. \frac{8}{5} \\ x = \frac{- 16}{5} \\ Vậy x = \frac{- 16}{5} \end{array}$

Câu 10:

$c) x - \frac{1}{2} - \frac{1}{6} - \frac{1}{12} - \frac{1}{20} = \frac{1}{30}$

Xem đáp án

$\begin{array}{l} c) x - \frac{1}{2} - \frac{1}{6} - \frac{1}{12} - \frac{1}{20} = \frac{1}{30} \\ x = \frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \frac{1}{30} \\ x = \frac{1}{2} + \frac{1}{2.3} + \frac{1}{3.4} + \frac{1}{4.5} + \frac{1}{5.6} \\ x = \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + \frac{1}{5} - \frac{1}{6} \\ x = \frac{1}{2} + \frac{1}{2} - \frac{1}{6} \\ x = 1 - \frac{1}{6} \\ x = \frac{5}{6} \\ Vậy x = \frac{5}{6} \end{array}$

Câu 11:

Khi khảo sát một nhóm gồm 40 học sinh lớp 6 về việc học môn toán đã cho kết quả gồm ba loại như sau: 60% học sinh thích học toán, số học sinh thấy việc học toán cũng bình thường bằng số học sinh thích học toán; còn lại là các học sinh không thích và sợ học toán.

a) Tính số học sinh mỗi loại trong nhóm được khảo sát.

Xem đáp án

a) Số học sinh thích học môn toán là:

40. 60% = 24 (học sinh);

Số học sinh thấy việc học môn toán cũng bình thường là:

24. $\frac{1}{2}$ = 12 (học sinh);

Số học sinh không thích và sợ học toán là:

40 – 24 – 12 = 14 (học sinh).

Vậy trong nhóm được khảo sát có 24 học sinh thích học môn toán, 12 học sinh thấy việc học môn toán cũng bình thường, 14 học sinh không thích và sợ học toán.

Câu 12:

b) Tính số phần trăm giữa số học sinh không thích và sợ học toán so với tổng số học sinh được khảo sát.

Xem đáp án

b) Tỉ số phần trăm giữa số học sinh không thích và sợ học toán so với tổng số học sinh được khảo sát là:

$\frac{14}{40} .100 = 56 %$

Vậy tỉ số phần trăm giữa số học sinh không thích và sợ học toán so với tổng số học sinh được khảo sát là 56%.

Câu 13:

Vẽ góc xAy có số đo bằng 60^o. Trên tia Ax lấy điểm B sao cho AB = 3 cm, trên tia Ay lấy điểm C sao cho AC = 5 cm. Gọi D là trung điểm của đoạn thẳng BC. Nối A với D.

a) Viết tên (cách viết ký hiệu) tất cả các góc đỉnh D và chỉ ra cạnh của mỗi góc đó.

Xem đáp án

a)

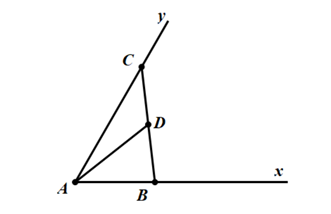
Vẽ góc xAy có số đo bằng 60o. Trên tia Ax lấy điểm B sao cho AB = 3 cm, trên tia Ay lấy điểm C sao cho AC = 5 cm (ảnh 1)

Theo hình vẽ các góc đỉnh D bao gồm:

Góc $\hat{ADB}$ có cạnh DA và DB;

Góc $\hat{ADC}$ có cạnh DA và DC;

Góc $\hat{BDC}$ có cạnh DB và DC;

Câu 14:

b) Đo các góc ABC; BAD; ADC (làm tròn đến hàng đơn vị) và cho biết các góc đó là góc gì? Vì sao?

Xem đáp án

b) Đo các góc ABC, BAD, ADC (làm tròn đến hàng đơn vị), ta được:

$\hat{ABC}$ = 83^o; $\hat{BAD}$ = 36^o; $\hat{ADC}$ = 119^o.

Vì $\hat{ABC}$ = 83^o < 90^o nên $\hat{ABC}$ là góc nhọn;

Vì $\hat{BAD}$ = 36^o < 90^o nên $\hat{BAD}$ là góc nhọn;

Vì 90^o < $\hat{ADC}$ = 119^o < 180^o nên $\hat{ADC}$ là góc tù.

Câu 15:

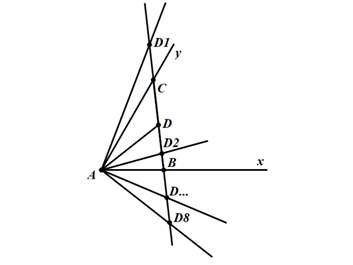
c) Lấy 8 điểm phân biệt D₁, D₂, …,D₈ trên đường thẳng BC (D₁, D₂, …,D₈ không trùng với các điểm B, C, D). Kẻ các tia AD₁, AD₂, …,AD₈. Hỏi có tất cả bao nhiêu góc có đỉnh A được tạo thành? Vì sao?

Xem đáp án

c) Khi lấy 8 điểm phân biệt D₁, D₂, …, D₈ trên đường thẳng BC (D₁, D₂, …, D₈ không trùng với các điểm B, C, D) thì kẻ được các tia AD₁, AD₂, …, AD₈.

Nên các tia đỉnh A trên hình gồm 8 tia AD₁, AD₂, …, AD₈ và 3 tia Ax, AD, Ay.

Suy ra, tổng số tia gốc A trong hình trên là 11 tia.

Tổng số góc có đỉnh A được tạo thành trên hình là:

$\frac{11 . (11 - 1)}{2} = \frac{110}{2} = 55$ (góc đỉnh A).

Vậy tổng số góc có đỉnh A được tạo thành trên hình có 55 góc đỉnh A.

c) Lấy 8 điểm phân biệt D1, D2, …,D8 trên đường thẳng BC (D1, D2, …,D8 không trùng với các điểm B, C, D). (ảnh 1)

Câu 16:

Cho $M = \frac{(\frac{3}{1.4} + \frac{3}{2.6} + \frac{3}{3.8} + \frac{3}{4.10} + ... + \frac{3}{49.100})}{(1 - \frac{1}{4}) (1 - \frac{1}{5}) (1 - \frac{1}{6}) ... (1 - \frac{1}{100})}$ . Chứng tỏ rằng M có giá trị là một số nguyên.

Xem đáp án

Đặt $A = \frac{3}{1.4} + \frac{3}{2.6} + \frac{3}{3.8} + \frac{3}{4.10} + ... + \frac{3}{49.100}$ ;

$B = (1 - \frac{1}{4}) (1 - \frac{1}{5}) (1 - \frac{1}{6}) ... (1 - \frac{1}{100})$ ;

Ta có $A = \frac{3}{1.4} + \frac{3}{2.6} + \frac{3}{3.8} + \frac{3}{4.10} + ... + \frac{3}{49.100}$

$\begin{array}{l} = \frac{6}{2.4} + \frac{4}{4.6} + \frac{6}{6.8} + \frac{6}{8.10} + ... + \frac{6}{98.100} \\ = 3. (\frac{2}{2.4} + \frac{2}{4.6} + \frac{2}{6.8} + \frac{2}{8.10} + ... + \frac{2}{98.100}) \\ = 3. (\frac{1}{2} - \frac{1}{4} + \frac{1}{4} - \frac{1}{6} + \frac{1}{6} - \frac{1}{8} + \frac{1}{8} - \frac{1}{10} + ... + \frac{1}{98} - \frac{1}{100}) \\ = 3. (\frac{1}{2} - \frac{1}{100}) \\ = 3. \frac{49}{100} \end{array}$ .

Với: $B = (1 - \frac{1}{4}) (1 - \frac{1}{5}) (1 - \frac{1}{6}) ... (1 - \frac{1}{100})$

$= \frac{3}{4} . \frac{4}{5} . \frac{5}{6} ... \frac{99}{100}$ .

Suy ra $M = \frac{A}{B} = 3. \frac{49}{100} : \frac{3}{100} = \frac{3.49}{100} . \frac{100}{3} = 49$

Ta thấy 49 $\in$ ℕ.

Do đó biểu thức M là một giá trị nguyên.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Toán 6 Học kì 2

Đề thi Toán 6 Học kì 2 có đáp án (Đề 9)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương