19 câu hỏi trắc nghiệm thuộc Dạng 2: Ước chung lớn nhất có đáp án

Câu 1:

Tìm ƯCLN của các số

a) ƯCLN $(18, 30)$

Phân tích các số ra thừa số nguyên tố

$18 = {2.3}^{2}$ $, 30 = 2.3.5$

Từ đó ƯCLN

(18, 30) = 2.3 = 6

Câu 2:

b) ƯCLN $(24, 48)$

Xem đáp án

b) ƯCLN $(24, 48)$

Phân tích các số ra thừa số nguyên tố

$24 = 2^{3} .3$ , $48 = 2^{4} .3$
Từ đó ƯCLN $(24, 48) = 2^{3} .3 = 24$

Câu 3:

c) ƯCLN

(18, 30, 15)

Xem đáp án

c) ƯCLN $(18, 30, 15)$

Phân tích các số ra thừa số nguyên tố.

$18 = {2.3}^{2}$

$30 = 2.3.5$

$, 15 = 3.5$

Từ đó ƯCLN $(18, 30, 15) = 3$

Câu 4:

d) ƯCLN $(24, 48, 36)$

Xem đáp án

d) ƯCLN $(24, 48, 36)$

Phân tích các số ra thừa số nguyên tố.

$24 = 2^{3} .3,$

$48 = 2^{4} .3,$

$36 = 2^{2} {.3}^{2}$

Từ đó ƯCLN

(24, 48, 36) = 2^{2} .3 = 12

Câu 5:

Sử dụng thuật toán Ơclit để tìm

a) ƯCLN

(174, 18)

Xem đáp án

a) Ta thực hiện theo các bước:

Lấy 174 chia cho 18 ta được $174 = 9.18 + 12$

Lấy 18 chia cho 12 ta được $18 = 1.12 + 6$

Lấy 12 chia cho 6 ta được $12 = 2.6 + 0$

Vậy ta được ƯCLN $(174, 18) = 6$

Câu 6:

b) ƯCLN

(124, 16)

Xem đáp án

b) Ta thực hiện theo các bước:

Lấy 124 chia cho 16 ta được $124 = 7.16 + 12$

Lấy 16 chia cho 12 ta được $16 = 1.12 + 4$

Lấy 12 chia cho 4 ta được $12 = 3.4 + 0$

Vậy ta được ƯCLN $(124, 16) = 4$

Câu 7:

Tìm các ước chung của 24 và 180 thông qua tìm ƯCLN

Xem đáp án

Phân tích các số ra thừa số nguyên tố.

$24 = 2^{3} .3,$ $180 = 2^{2} {.3}^{2} .5$

Từ đó ƯCLN $(24, 18 0) = 2^{2} .3 = 12$

Mà Ư $(12) = \{1; 2; 3; 4; 6; 12\}$

Vậy ƯC $(24, 180) = \{1; 2; 3; 4; 6; 12\}$

Câu 8:

Tìm số tự nhiên x thõa mãn $90 ⋮ x; 150 ⋮ x$ và $5 < x < 30$ .

Xem đáp án

Số tự nhiên x thõa mãn $90 ⋮ x; 150 ⋮ x$ nên $x \in$ ƯCLN $(90, 15 0)$

Phân tích các số ra thừa số nguyên tố.

$90 = {2.3}^{2} .5,$ $150 = {2.3.5}^{2}$

Từ đó ƯCLN $(90, 15 0) = 2.3.5 = 30$

Mà Ư(30)={1;2;3;5;6;10;15;30}

Vì $5 < x < 30$ nên $x \in \{6; 10; 15\}$

Câu 9:

Tìm số tự nhiên a,b biết ƯCLN $(a, b) = 3$ và $a . b = 891$

Xem đáp án

Ta có ƯCLN $(a, b) = 3$ nên $a = 3 k, b = 3 m$ và ƯCLN $(k, m) = 1$

Giả sử $a > b \Rightarrow k > m$ . Ta có $a . b = 891$ $\Rightarrow 3 k .3 m = 891 \Rightarrow k . m = 3^{2} .11$

TH1: $k = 11, m = 9$ $\Rightarrow a = 33; b = 27$

TH2: $k = 99, m = 1$ $\Rightarrow a = 297; b = 3$

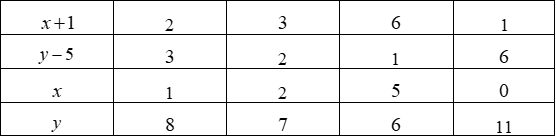
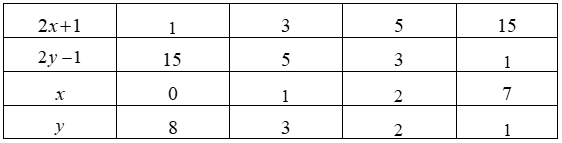
Câu 10:

Tìm số tự nhiên n để biểu thức $A = \frac{15}{2 n + 1}$ có giá trị là một số tự nhiên.

Xem đáp án

Để A là một số tự nhiên thì 2n+1 phải là ước của 15

Ta có Ư $(15) = \{1; 3; 5; 15\}$

Do đó:

+ Với $2 n + 1 = 1$ $\Rightarrow n = 0, A = 15$

+ Với $2 n + 1 = 3$ $\Rightarrow n = 1, A = 5$

+ Với $2 n + 1 = 5$ $\Rightarrow n = 2, A = 3$

+ Với $2 n + 1 = 15$ $\Rightarrow n = 7, A = 1$

Câu 11:

Tìm số tự nhiên $x, y$

a)

(x + 1) (y - 5) = 6

Xem đáp án

a) $(x + 1) (y - 5)$ =6=2.3=3.2=6.1=1.6

Ta có bảng sau:

Vậy $(x; y) = \{(1; 8), (2; 7), (5; 6), (0; 11)\}$

Câu 12:

b) $(2 x + 1) (2 y - 1) = 15$

Xem đáp án

b) $(2 x + 1) (2 y - 1) = 15$

=1.15=3.5=5.3=15.1

Ta có bảng sau:

Vậy $(x; y) = \{(0; 8), (1; 3), (2; 2), (7; 1)\}$

Câu 13:

Cô giáo chủ nhiệm muốn chia 24 quyển vở, 48 bút bi và 36 gói bánh thành một số phần thưởng như nhau để trao trong dịp sơ kết học kì. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng? Khi đó mỗi phần thưởng có bao nhiêu quyển vở, bút bi và gói bánh.

Xem đáp án

Gọi a là số phần thưởng để cô giáo chủ nhiệm trao trong dịp sơ kết học kì $(a \in Ν^{*}; a < 24)$

Để số phần thưởng là nhiều nhất thì a phải là số lớn nhất sao cho $24 ⋮ a; 48 ⋮ a; 36 ⋮ a$

Tức là $a =$ ƯCLN $(24, 48, 36)$

Ta có $24 = 2^{3} .3, 48 = 2^{4} .3, 36 = 2^{2} {.3}^{2}$

Từ đó ƯCLN $(24, 48, 36) = 2^{2} .3 = 12$ $\Rightarrow a = 12$

Vậy có thể chia được nhiều nhất 12 phần thưởng.

Trong đó có 2 quyển vở, 4 bút bi, 3 gói bánh.

Câu 14:

Một hình chữ nhật có chiều dài 150m và chiều rộng 90m được chia thành các hình vuông có diện tích bằng nhau. Tính độ dài cạnh hình vuông lớn nhất trong cách chia trên ? (số đo cạnh là số tự nhiên với đơn vị là m)

Xem đáp án

Để chia hình chữ nhật thành các hình vuông có diện tích bằng nhau thì độ dài mỗi cạnh hình vuông phải là ước chung của 150 và 90

Do đó độ dài cạnh hình vuông lớn nhất là ƯCLN $(90, 150) = 30$

Vậy độ dài cạnh hình vuông lớn nhất là 30m

Câu 15:

Chứng minh 22 và 5 là hai số nguyên tố cùng nhau.

Xem đáp án

Phân tích các số ra thừa số nguyên tố.

$22 = 2.11.1,$ $5 = 1.5$

Từ đó ƯCLN $(22, 5) = 1$

Vậy 22 và 5 là hai số nguyên tố cùng nhau.

Câu 16:

Chứng minh rằng với mọi số tự nhiên , các số sau là các số nguyên tố cùng nhau.

a) n+1 và n+2

Xem đáp án

a) n+1 và n+2

Gọi d= ƯCLN $(n + 1, n + 2)$

$\Rightarrow \{\begin{cases} n + 2 ⋮ d \\ n + 1 ⋮ d \end{cases}$ $\Rightarrow (n + 2) - (n + 1) ⋮ d$ $\Rightarrow 1 ⋮ d$ $\Rightarrow d = 1$

Từ đó ƯCLN $(n + 1, n + 2) = 1$

Vậy n+1 và n+2 là các số nguyên tố cùng nhau với mọi $n \in Ν$ .

Câu 17:

b) 2n+2 và 2n+3

Xem đáp án

b) 2n+2 và 2n+3

Gọi d= ƯCLN $(2 n + 2, 2 n + 3)$

$\Rightarrow \{\begin{cases} 2 n + 2 ⋮ d \\ 2 n + 3 ⋮ d \end{cases}$ $\Rightarrow (2 n + 3) - (2 n + 2) ⋮ d$ $\Rightarrow 1 ⋮ d$ $\Rightarrow d = 1$

Từ đó ƯCLN $(2 n + 2, 2 n + 3) = 1$

Vậy 2n+2 và 2n+3 là các số nguyên tố cùng nhau với mọi $n \in Ν$ .

Câu 18:

c) 2n+1 và n+1

Xem đáp án

c) 2n+1 và n+1

Gọi d=ƯCLN $(2 n + 1, n + 1)$

$\Rightarrow \{\begin{cases} n + 1 ⋮ d \\ 2 n + 1 ⋮ d \end{cases}$ $\Rightarrow \{\begin{cases} 2 (n + 1) ⋮ d \\ 2 n + 1 ⋮ d \end{cases}$ $\Rightarrow (2 n + 2) - (2 n + 1) ⋮ d$ $\Rightarrow 1 ⋮ d$ $\Rightarrow d = 1$

Từ đó ƯCLN $(2 n + 1, n + 1) = 1$

Câu 19:

d) n+1 và 3n+4

Xem đáp án

d) n+1 và 3n+4

Gọi d= ƯCLN $(n + 1, 3 n + 4)$

$\Rightarrow \{\begin{cases} n + 1 ⋮ d \\ 3 n + 4 ⋮ d \end{cases}$ $\Rightarrow \{\begin{cases} 3 (n + 1) ⋮ d \\ 3 n + 4 ⋮ d \end{cases}$ $\Rightarrow (3 n + 4) - (3 n + 3) ⋮ d$ $\Rightarrow 1 ⋮ d$ $\Rightarrow d = 1$

Từ đó ƯCLN $(n + 1, 3 n + 4) = 1$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập chuyên đề Toán 6 Dạng 2: Ước và bội trong tập hợp số tự nhiên có đáp án

Dạng 2: Ước chung lớn nhất có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương