Bài tập chuyên đề Toán 6 Dạng 2: Hình vuông. Hình chữ nhật. Hình thang có đáp án
Bài tập chuyên đề Toán 6 Hình thang có đáp án
-
1084 lượt thi
-
17 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong các hình sau, hình nào là hình thang? Vì sao

Lời giải
Hình 1, 4 là các hình thang vì có hai cạnh đối song song.
Câu 2:
Cho hình vẽ sau, biết \[MN{\rm{//}}PQ\]
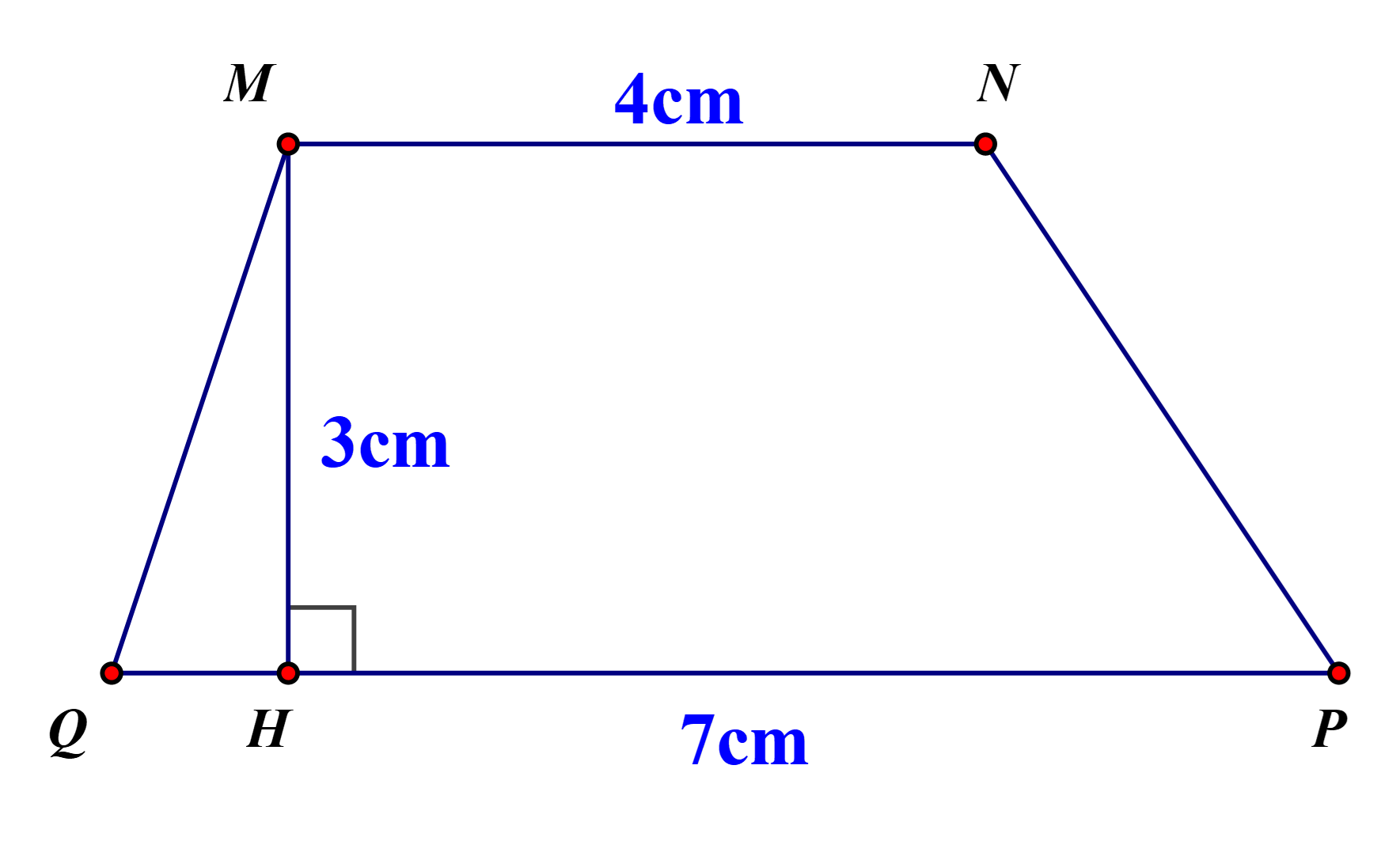
Tứ giác MNPQ có là hình thang không? Nêu các yếu tố?
Lời giải
Tứ giác \[MNPQ\] là hình thang vì \[MN{\rm{//}}PQ\]
Hình thang \[MNPQ\] có hai đáy \[MN = 4cm,PQ = 7cm\], chiều cao \[AH = 3cm\]
Câu 3:
Vẽ hình thang \[ABCD\] trên giấy kẻ ô vuông có đáy lớn \[DC{\rm{ }} = {\rm{ }}10cm\], đáy bé \[AB{\rm{ }} = {\rm{ }}6cm\] và chiều cao \[AH{\rm{ }} = {\rm{ }}3cm\].
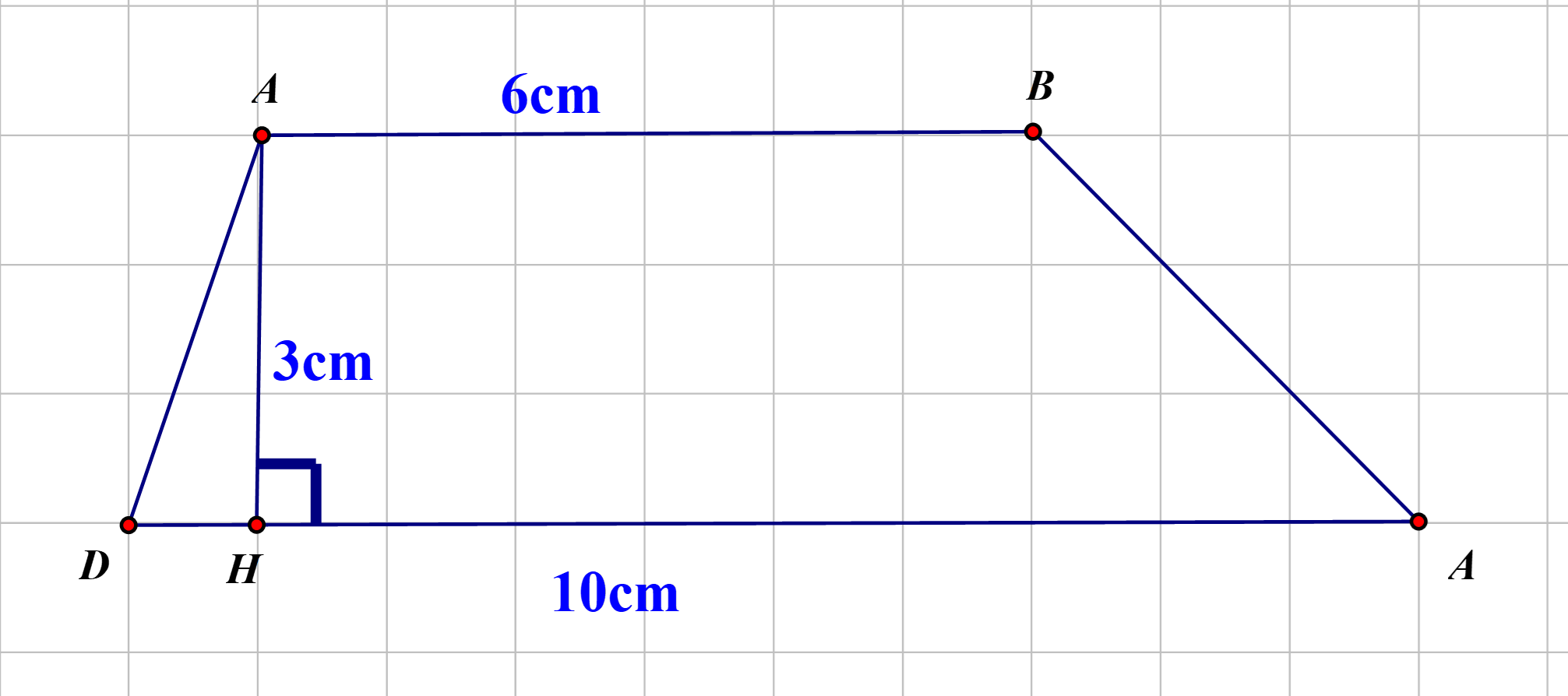
Câu 4:
Lời giải
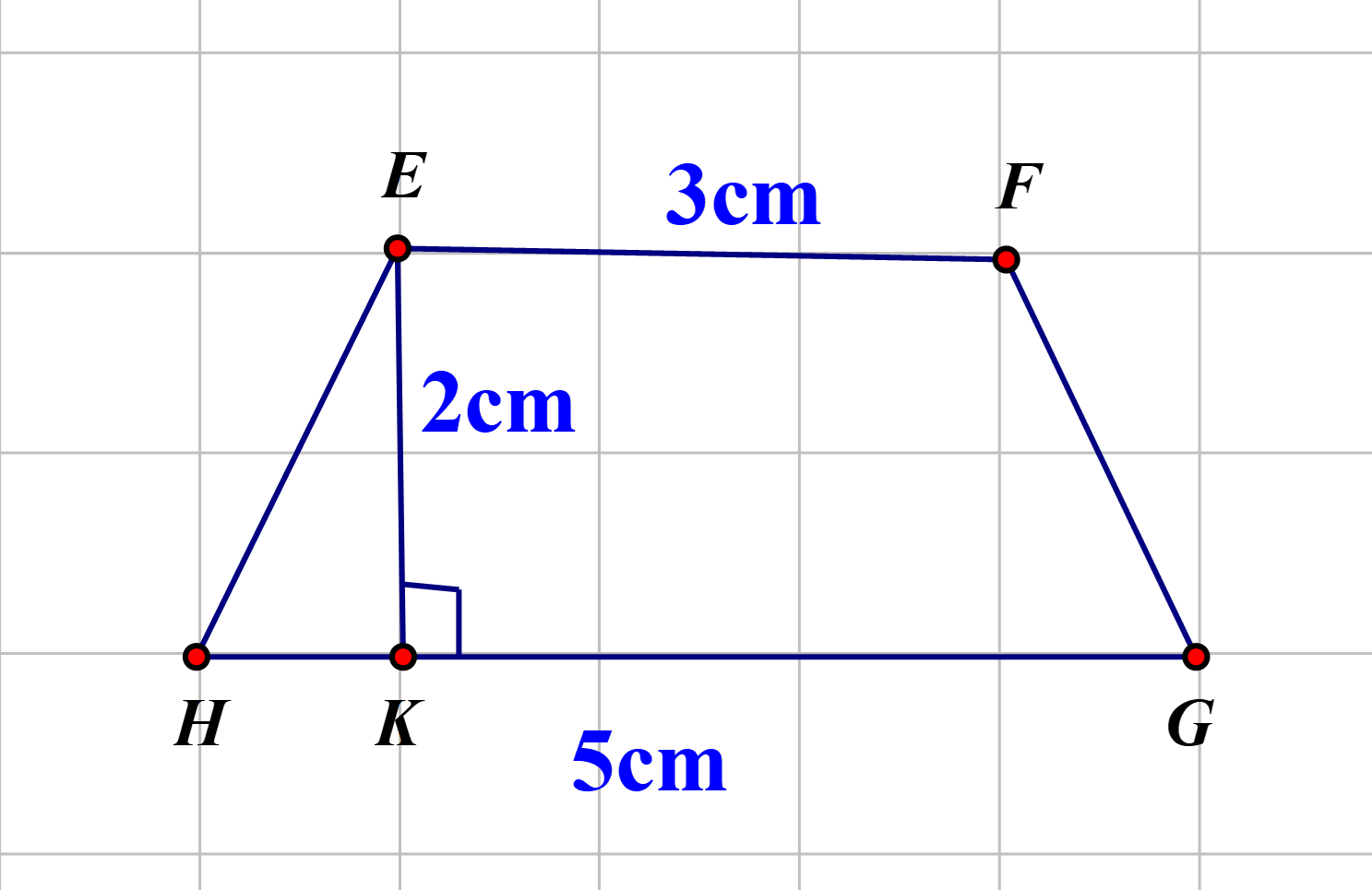
Câu 5:
Tính diện tích hình thang biết :
Độ dài hai đáy lần lượt là \[{\rm{9}}{\rm{,4 }}m\] va \[{\rm{6}}{\rm{,6 }}m\]; chiều cao là \[10,5{\rm{ }}cm\].
Diện tích hình thang độ dài hai đáy lần lượt là \[{\rm{9}}{\rm{,4 }}m\] va \[{\rm{6}}{\rm{,6 }}m\]; chiều cao là \[10,5{\rm{ }}cm\] là:
\[S = \left( {9,4 + 6,6} \right) \cdot 10,5:2 = 84\]\[(c{m^2})\]
Câu 6:
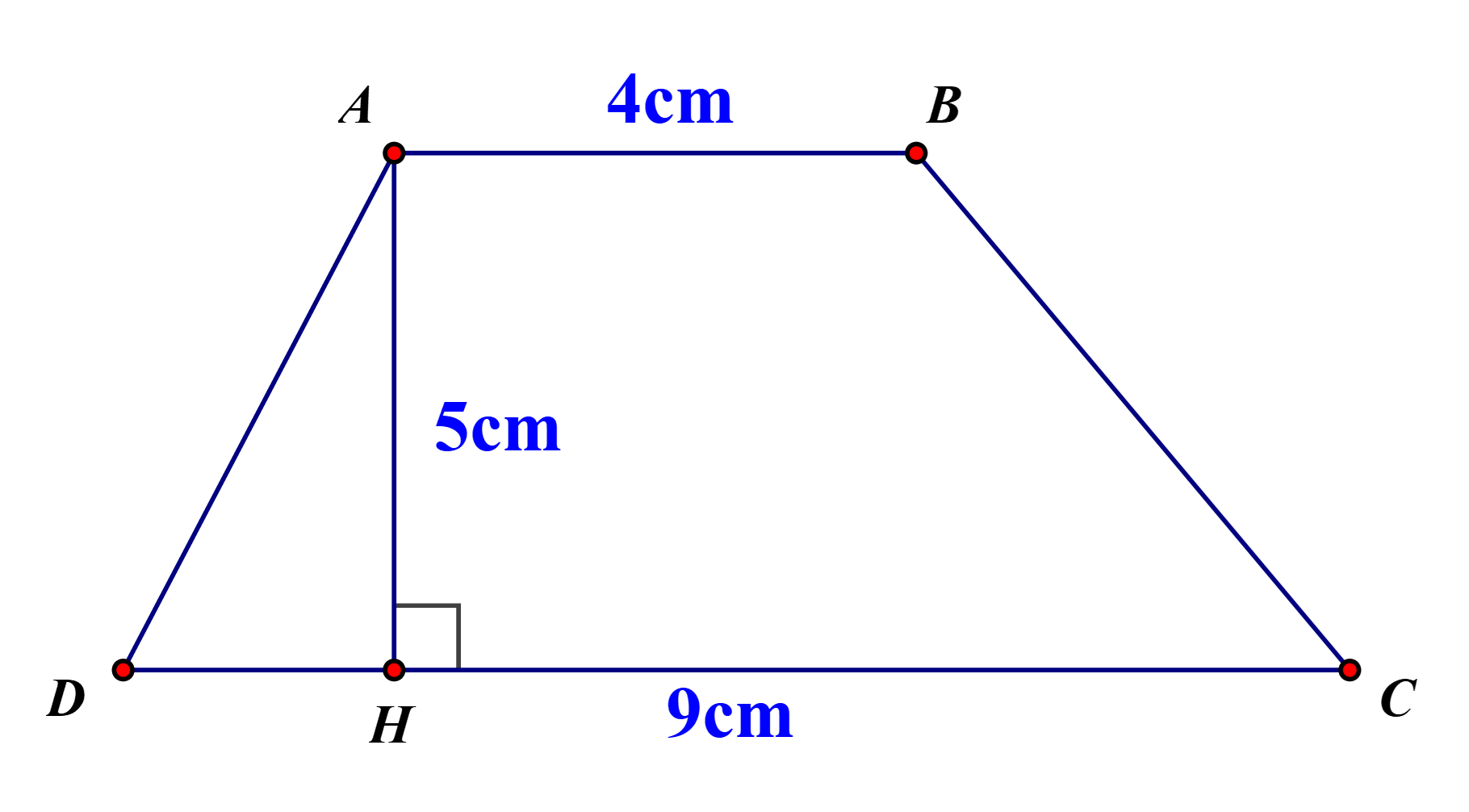
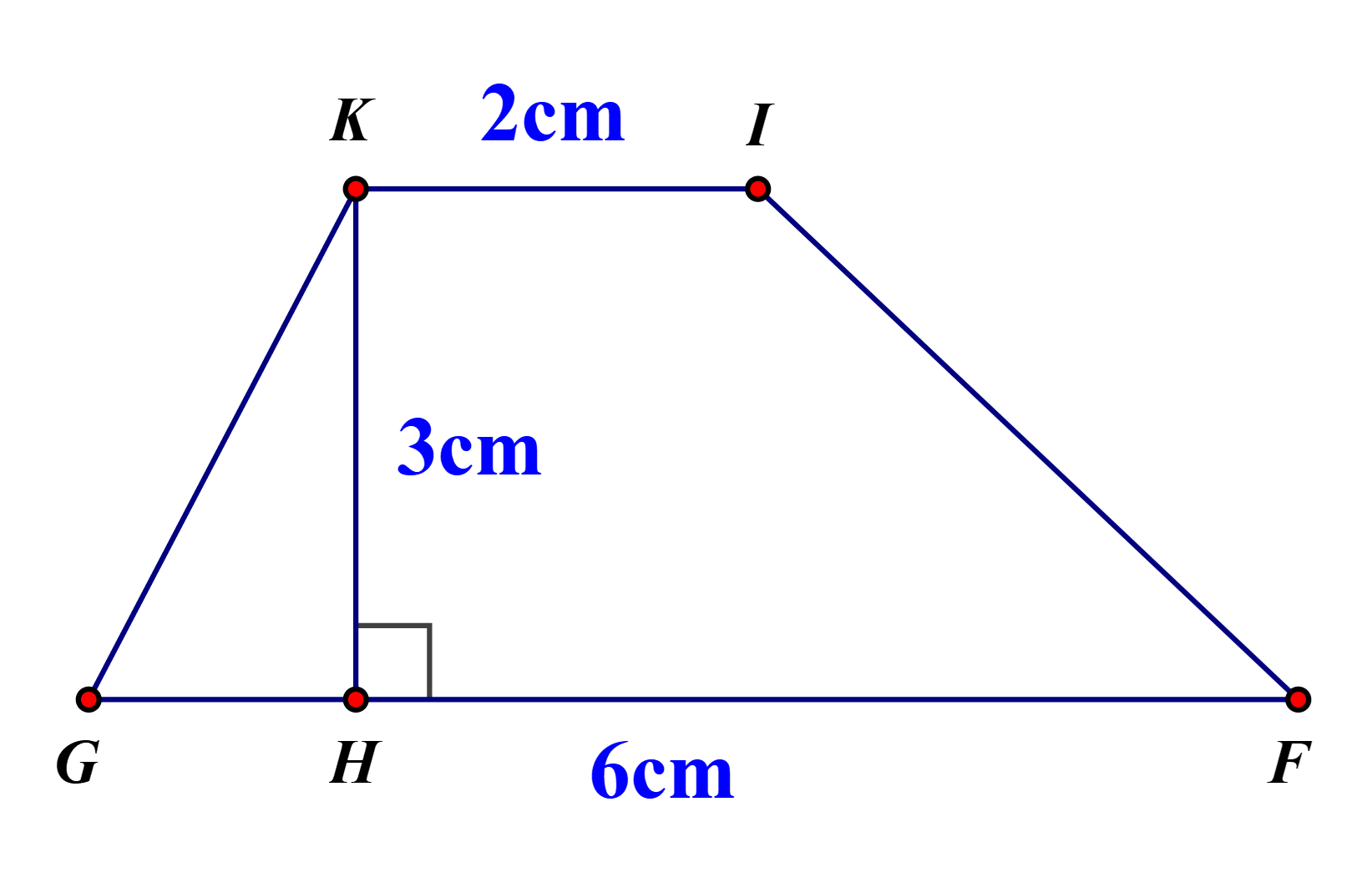
Lời giải
Diện tích hình thang \[ABCD\] là: \[\left( {4 + 9} \right) \cdot 5:2 = 32,5\]\[(c{m^2})\]
Diện tích hình thang \[KIFG\] là: \[\left( {2 + 6} \right) \cdot 3:2 = 12\]\[(c{m^2})\]
Câu 7:
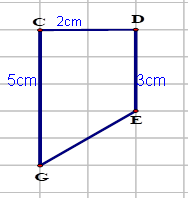
Lời giải: Diện tích hình thang \[ABCD\] là: \[\left( {3 + 5} \right) \cdot 2:2 = 8\]\[(c{m^2})\]
Câu 8:
Lời giải
Chiều cao của hình thang là: \[\left( {110 + 90} \right):2 = 100\]\[(cm)\]
Diện tích của thửa ruộng hình thang đó là: \[\left( {110 + 90} \right) \cdot 100:2 = 10000\]\[(c{m^2})\]
Câu 9:
Lời giải:
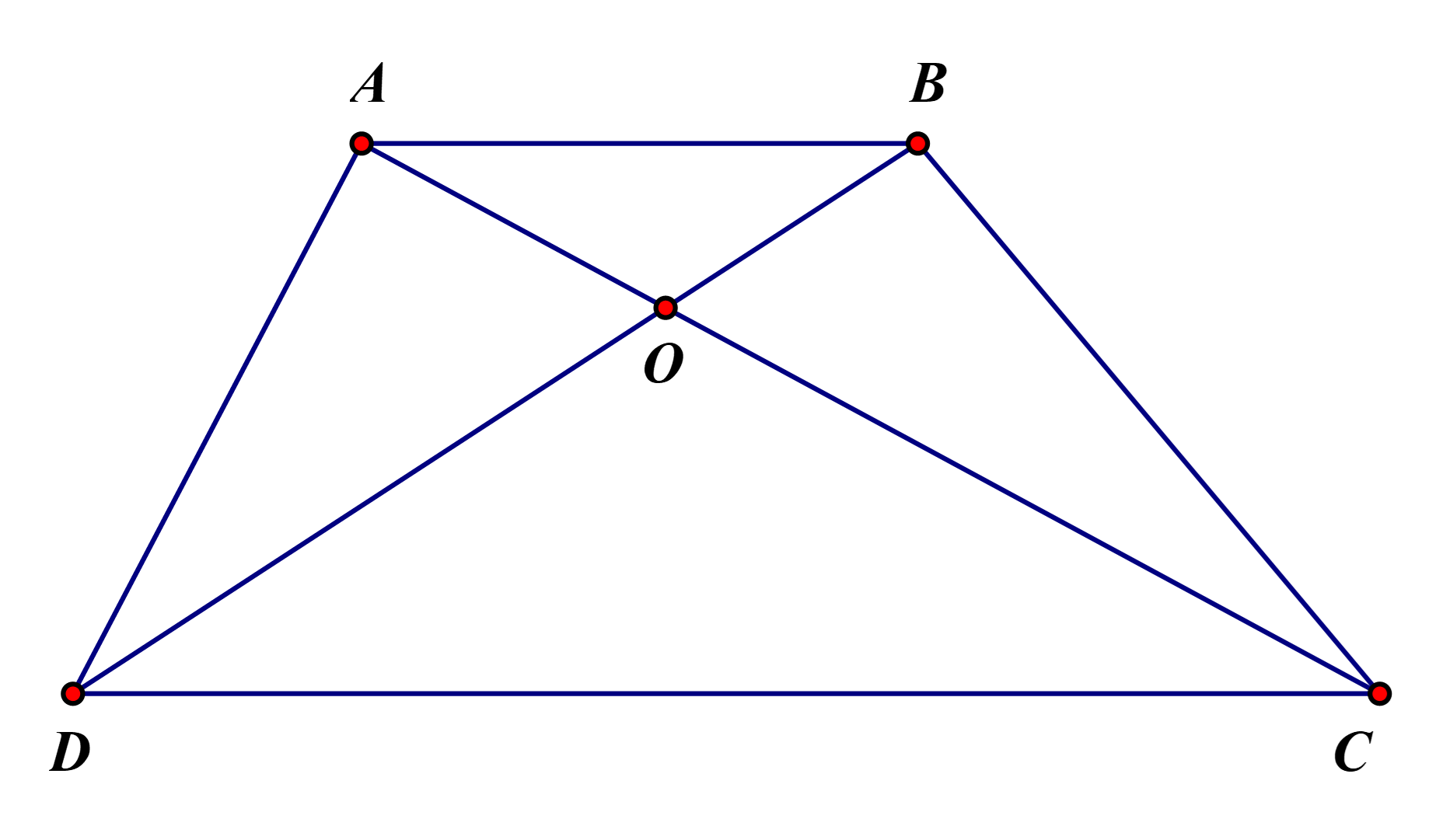
Ta có, tam giác \[\Delta ADC\] và tam giác \[\Delta BDC\]đều có chung đáy và chiều cao
Suy ra, \[{S_{ADC\;}} = {\rm{ }}{S_{BDC}}\;\] (1)
Chứng minh tương tự, ta có: \[{S_{DAB}}\; = {\rm{ }}{S_{CAB}}\;\] (2)
Ta có: \[{S_{AOD\;}} = {\rm{ }}{S_{ADC}}\; - {\rm{ }}{S_{DOC}}\;\] (3)
Từ (1), (2) và (3), suy ra: \[{S_{BOC}}\; = {\rm{ }}{S_{AOD}}\]
Do đó: \[{S_{ADC}}\; = {\rm{ }}{S_{BDC}},{\rm{ }}{S_{DAB}}\; = {\rm{ }}{S_{CAB}},{\rm{ }}{S_{AOD}}\; = {\rm{ }}{S_{BOC}}\]
Câu 10:
Cho hình thang như hình vẽ sau, biết diện tích tam giác \[AOD\] là \[10\]\[c{m^2}\] và diện tích tam giác \[ODC\]là \[20\] \[c{m^2}\]
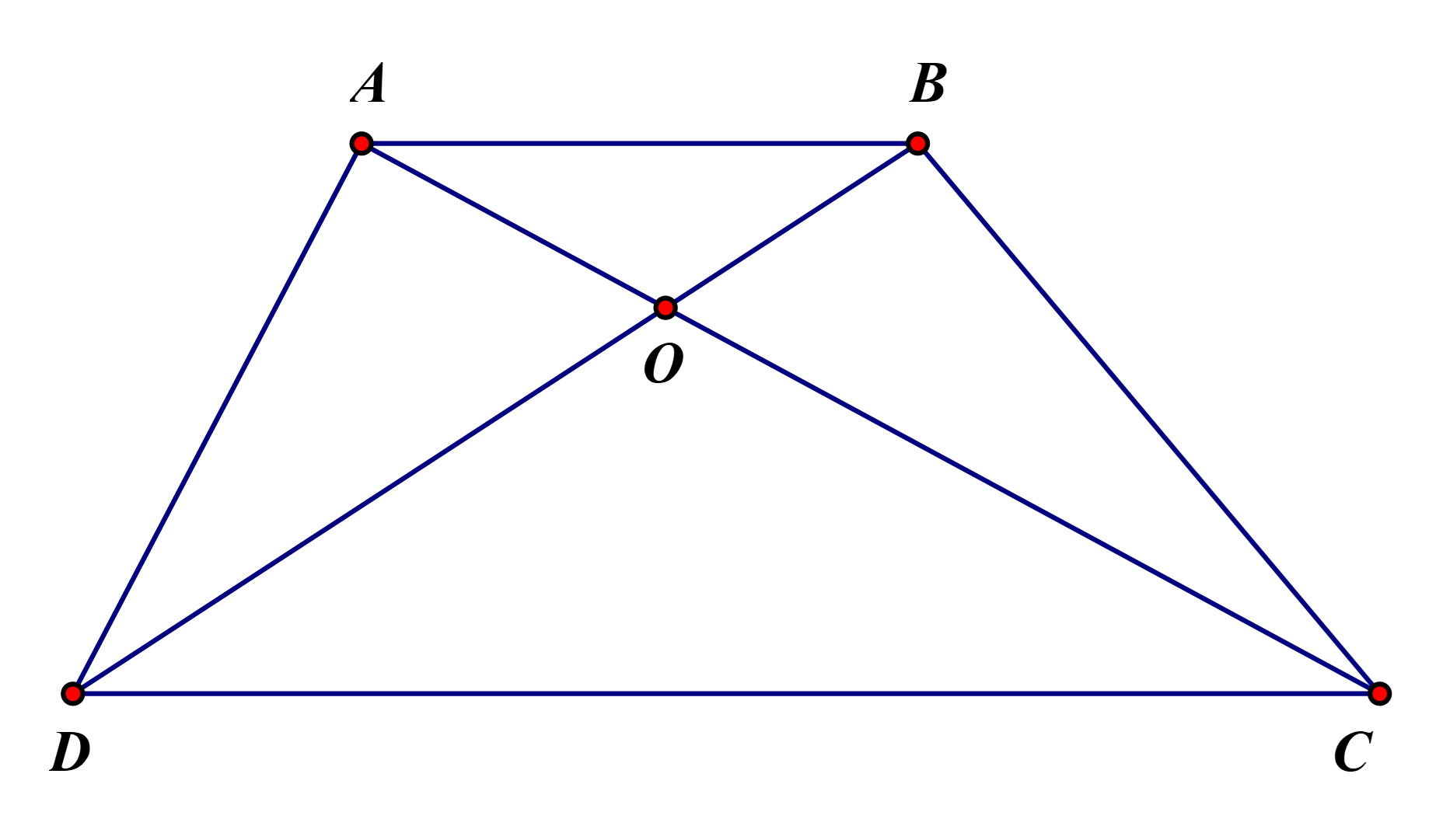
Lời giải
Xét hai tam giác \[ADC\] và\[BDC\], ta thấy hai tam giác đều có chiều cao bằng nhau và chung đáy DC nên diện tích tam giác \[ADC\] bằng diện tích tam giác\[BDC\]
Do \[{S_{ADC}}\; = {\rm{ }}{S_{DOC}}\; + {\rm{ }}{S_{AOD}}\;\]và \[{S_{BDC}}\; = {\rm{ }}{S_{DOC\;}} + {\rm{ }}{S_{BOC}}\] nên \[{S_{AOD}}\; = {S_{BOC}}\; = 10\]\[(c{m^2})\]
Tam giác \[AOD\] và tam giác \[DOC\] đều có chung chiều cao hạ từ\[D\], \[{S_{DOC}}\; = 2.{S_{AOD}}\]
Suy ra \[OC = 2.AO\]
Tam giác \[ABO\] và tam giác \[BOC\]có chung chiều cao hạ từ\[B\], có đáy \[OC\] gấp 2 lần đáy\[AO\], suy ra \[{S_{BOC}}\; = {\rm{ }}2{S_{AOB}}\]
Do đó \[{S_{ABO}}\; = {S_{BOC}}\; = 5\]\[(cm)\].
Ta có \[{S_{ABCD}}\; = {S_{AOB}}\; + {\rm{ }}{S_{AOD}}\; + {S_{DOC}}\; + {S_{BOC}}\; = 5 + 10 + 20 + 10 = 45\]\[(c{m^2})\]
Câu 11:
Lời giải
Tổng độ dài hai đáy của hình thang là:\[455{\rm{ x }}2:13 = 70\] \[(m)\]
Độ dài đáy lớn của hình thang là:\[\left( {70 + 5} \right):2 = 37,5\] \[(m)\]
Độ dài đáy bé của hình thang là :\[37,5--5 = 32,5\]\[(m)\]
Câu 12:
Một thửa ruộng hình thang có các kích thước như hình dưới. Biết năng suốt lúa là \[0,8kg{\rm{/}}{m^3}\].
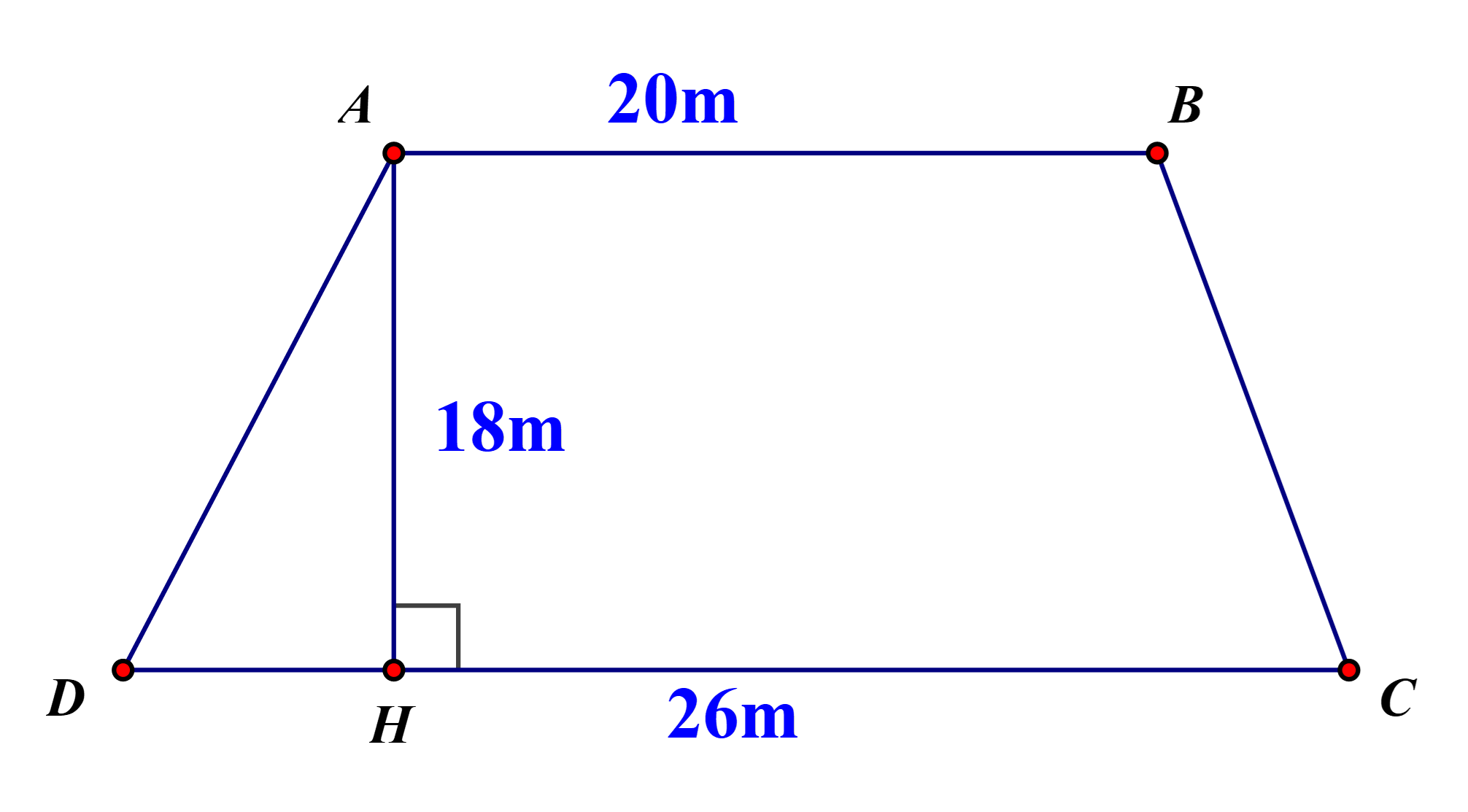
Tính diện tích mảnh ruộng.
Lời giải
Diện tích mảnh ruộng hình thang là: \[\left( {20 + 25} \right) \cdot 18:2 = 405\]\[({m^2})\]
Câu 13:
Lời giải
Câu 14:
Lời giải
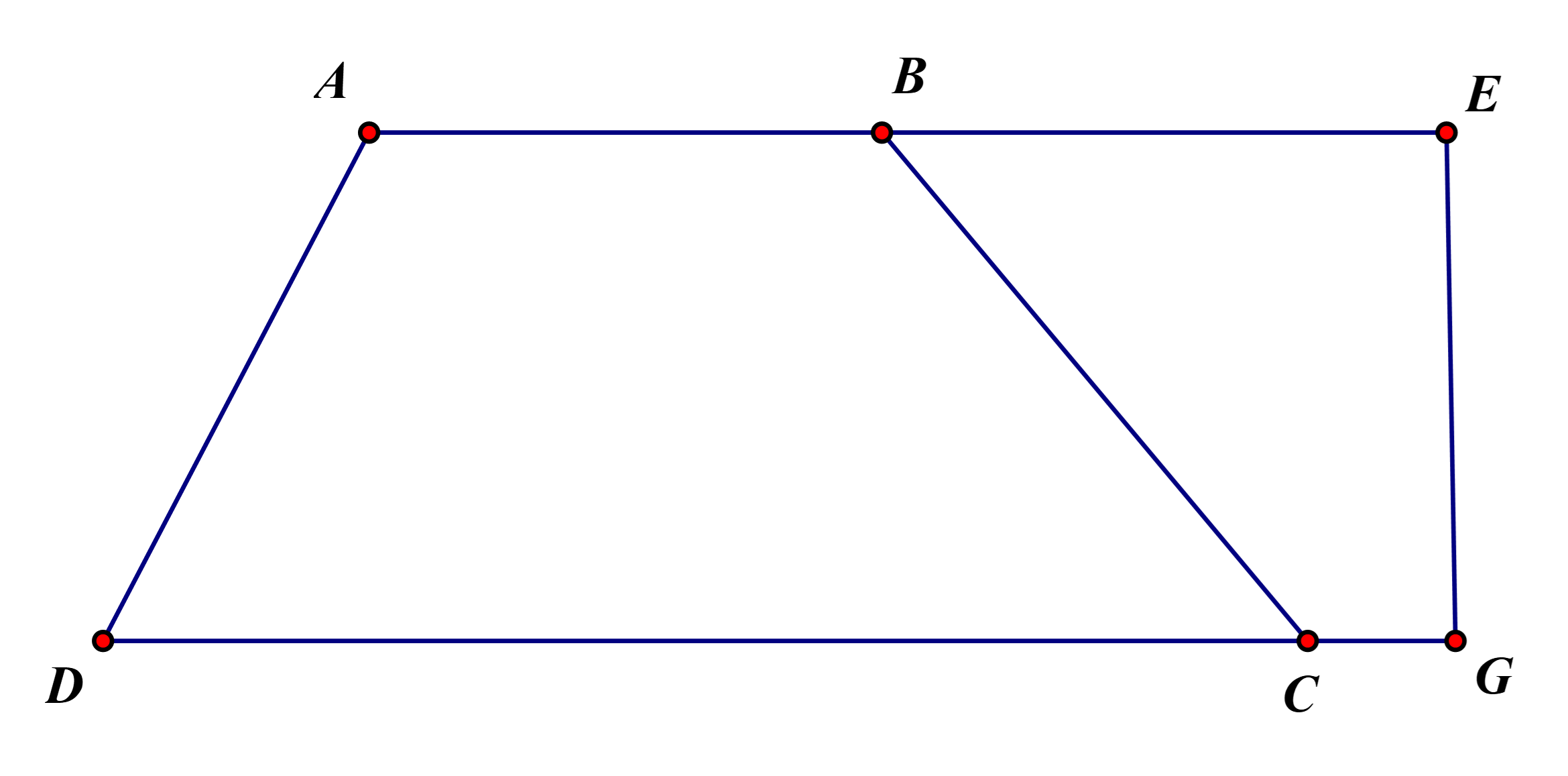
Gọi hình thang ban đầu là \[ABCD\], hình thang mới là \[AEGD\]
Hình thang \[AEGD\] có diện tích bằng diện tích của một hình chữ nhật có chiều rộng \[30m\] và chiều dài \[51m\].
Do đó diện tích hình thang \[AEGD\] là:\[30.51 = 1530({m^2})\]
Diện tích phần tăng thêm \[BEGC\] là:\[1530{\rm{ }}--{\rm{ }}1155{\rm{ }} = {\rm{ }}375\;({m^2})\]
Chiều cao BH của hình thang \[BEGC\] là:\[375{\rm{ }}{\rm{. }}2{\rm{ }}:{\rm{ }}\left( {20{\rm{ }} + {\rm{ }}5} \right){\rm{ }} = {\rm{ }}30{\rm{ }}\left( m \right)\]
Chiều cao \[BH\] cũng là chiều cao của hình thang \[ABCD\]. Do đó tổng hai đáy \[AB\] và \[CD\] là:
\[1155{\rm{ }}{\rm{. }}2{\rm{ }}:{\rm{ }}30{\rm{ }} = {\rm{ }}77{\rm{ }}\left( m \right)\]
Đáy bé là:\[\left( {77{\rm{ }}--{\rm{ }}33} \right){\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}22{\rm{ }}\left( m \right)\]
Đáy lớn là:\[77{\rm{ }}--{\rm{ }}22{\rm{ }} = {\rm{ }}55{\rm{ }}\left( m \right)\]
Vậy đáy bé:\[22m\]; đáy lớn:\[55m\].
Câu 15:
Lời giải
Tổng độ dài hai đáy của hình thang là :\[455{\rm{ }}x{\rm{ }}2{\rm{ }}:{\rm{ }}13{\rm{ }} = {\rm{ }}70{\rm{ }}\left( m \right)\]
Độ dài đáy lớn của hình thang là :\[\left( {70{\rm{ }} + {\rm{ }}5} \right){\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}37,5{\rm{ }}\left( m \right)\]
Độ dài đáy bé của hình thang là : \[37,5{\rm{ - }}5{\rm{ }} = {\rm{ }}32,5{\rm{ }}\left( m \right)\]
Vậy đáy bé:\[32,5m\]; đáy lớn:\[37,5m\].
Câu 16:
Một hình thang vuông có đáy bé bằng \[\frac{3}{5}\] đáy lớn và chiều cao bằng \[23cm\], người ta mở rộng hình thang để được một hình chữ nhật thì diện tích của nó tăng thêm lên \[414{m^2}\] . Hãy tính diện tích hình thang lúc đầu.
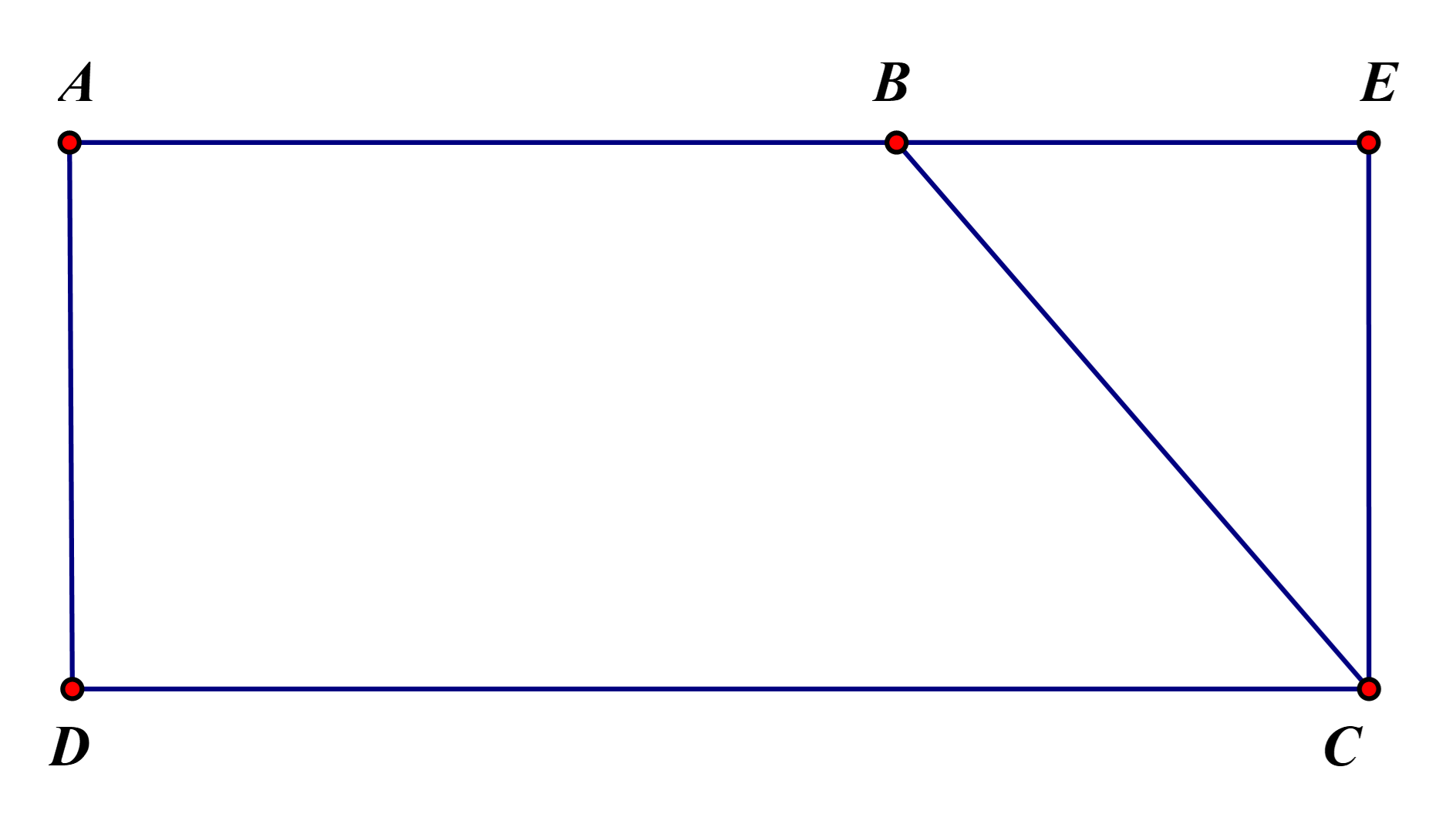
Lời giải
Phần mở rộng là một tam giác vuông, có cạnh góc vuông bằng chiều cao của hình thang.
Số đo cạnh góc vuông còn lại bằng: \[414:23 = 18\left( {cm} \right)\]
\[18cm\] chính là hiệu số đo hai đáy của hình thang. Coi đáy bé hình thang gồm ba phần bằng nhau thì đáy lớn gồm \[5\] phần. Hiệu số phần bằng nhau là: \[5{\rm{ }}--{\rm{ }}3{\rm{ }} = {\rm{ }}2{\rm{ }}\](phần)
Đáy lớn của hình thang bằng: \[\left( {18{\rm{ }}:{\rm{ }}2} \right){\rm{ }}x{\rm{ }}5{\rm{ }} = {\rm{ }}45{\rm{ }}\left( {cm} \right)\]
Đáy bé của hình thang bằng: \[45{\rm{ }}--{\rm{ }}18{\rm{ }} = {\rm{ }}27{\rm{ }}\left( {cm} \right)\]
Diện tích hình thang lúc đầu là: \[45.27 = 1215\left( {c{m^2}} \right)\]
Câu 17:
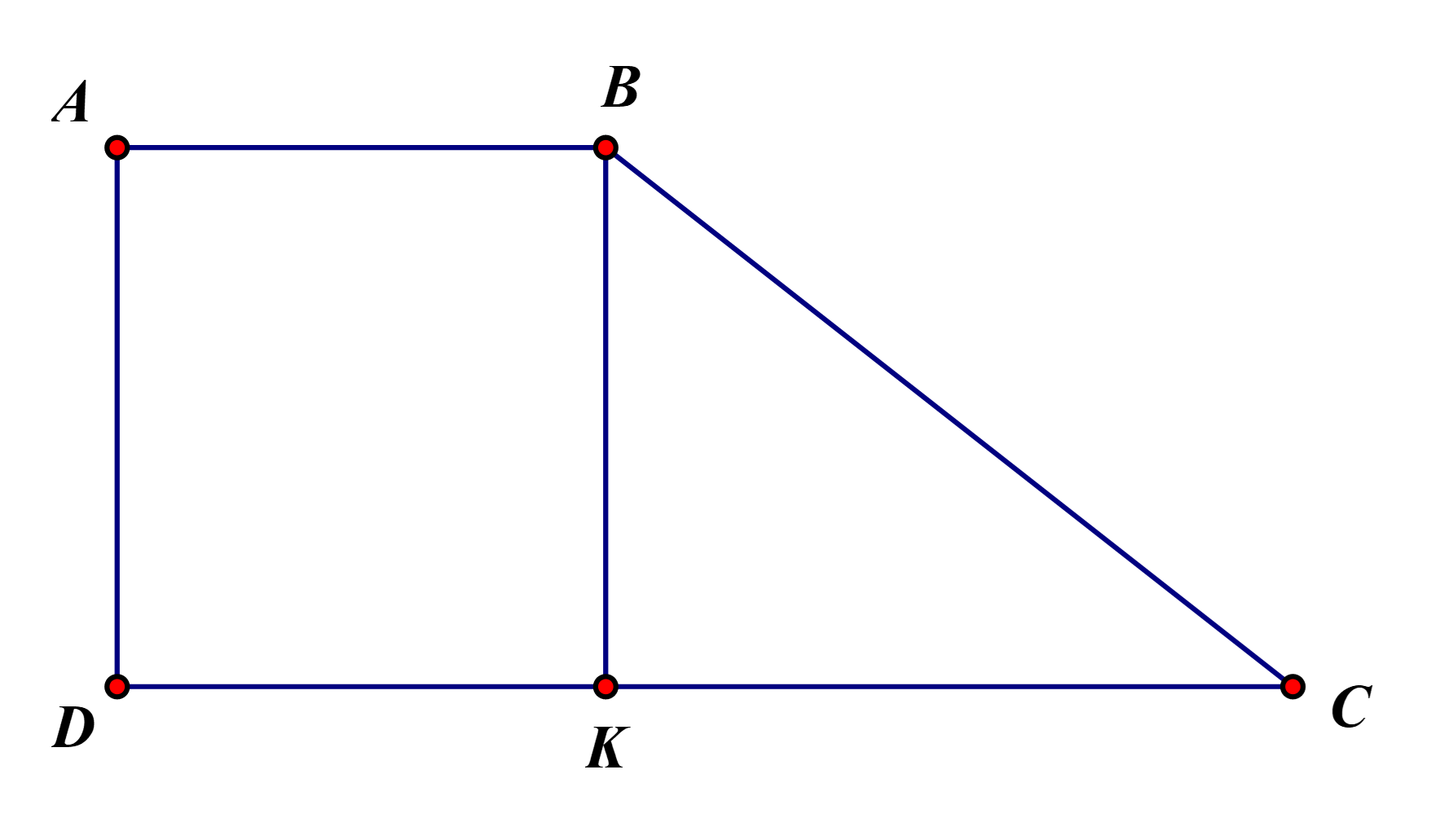
Lời giải
Độ dài cạnh \[AD\] là: \[168:12{\rm{ }} = {\rm{ }}14\left( {cm} \right)\]
Diện tích mảnh đất hình thang \[ABCD\] là: \[\left( {12 + 24} \right).14:2{\rm{ }} = \;266{\rm{ }}\left( {c{m^2}} \right)\].
