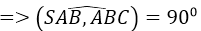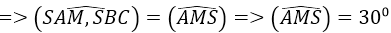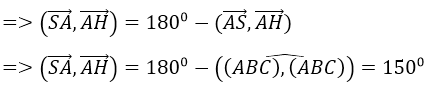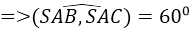Trắc nghiệm Ôn tập chương 3 có đáp án
-
940 lượt thi
-
13 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
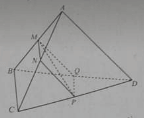
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.
Bộ ba vecto đồng phẳng là:
Các đường thẳng MN, NP, PQ, QM cùng nằm trong một mặt phẳng và BC, AD cùng song song với mặt phẳng (MNPQ). Suy ra ba vecto đồng phẳng
Đáp án B
Câu 2:
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.
Bộ ba vecto không đồng phẳng là:
Phương án A sai vì : Ba đường thẳng AB, MN, CA cùng trong mặt phẳng (ABC) nên ba vecto đồng phẳng
Phương án B sai vì: hai đường thẳng BC, AD cùng song song với mặt phẳng (MNPQ) có chứa đường thẳng MP nên ba vecto đồng phẳng
Phương án C sai vì : Đường thẳng AD // (MNPQ) và mặt phẳng này chứa hai đường thẳng MP, PQ nên ba vecto đồng phẳng
Phương án D đúng vì : Đường thẳng BD cắt mặt phẳng (MNPQ) và nó chứa hai đường thẳng MP, PQ nên không đồng phẳng
Đáp án D
Câu 4:
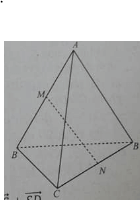
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp
Điều kiện GM = GN mới chứng tỏ điểm G nằm trên mặt phẳng trung trực của đoạn thẳng MN.
Đáp án A
Câu 5:
Cho hình chóp S.ABCD, với O là giao điểm của AC và BD. Mệnh đề nào sau đây là đúng?
Vì ABCD là hình bình hành có O là giao điểm của AC và BD nên O là trung điểm của AC và BD.
Theo tính chất trung điểm , ta có:
Chọn D.
Câu 7:
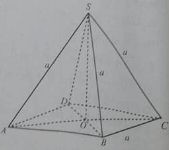
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD) vì:
Đáp án B
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Giả sử góc BAD bằng , khoảng cách từ S đến mặt phẳng (ABCD) bằng:
Đáp án A
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa hai mặt bên hình chóp S.ABCD và mặt phẳng đáy có tan bằng:
Đáp án A
Câu 10:
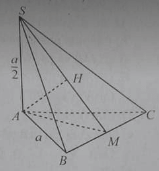
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
SA ⊥ (ABC) ⇒ (SAB) ⊥ (ABC)
Đáp án D
Câu 11:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
M là trung điểm của BC. Khi đó góc giữa hai mặt phẳng (SAM) và (SBC) bằng:
tam giác ABC đều nên AM ⊥ BC ⇒ SM ⊥ BC (theo định lí ba đường vuông góc)
Đáp án B
Câu 12:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Từ A hạ AH ⊥ SM. Khi đó góc giữa hai vecto và bằng:
AH ⊥ SM và AH ⊥ BC (do BC ⊥ (SAM)) ⇒ AH ⊥ (SBC)
Đáp án D
Câu 13:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
SA ⊥ (ABC) ⇒ SA ⊥ AB ⊂ (ABC) và SA ⊥ AC ⊂ (ABC)
Đáp án C