Bài tập chuyên đề toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng có đáp án
Dạng 1: Tìm giao tuyến của hai mặt phẳng có đáp án
-
745 lượt thi
-
25 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho S là một điểm không thuộc mặt phẳng chứa hình bình hành ABCD. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
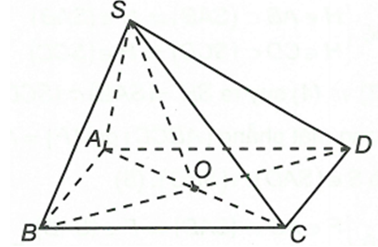
Ta có
Trong mặt phẳng (ABCD) có
Lại có
Từ (1) và (2) suy ra
Câu 2:
Trong mặt phẳng cho tức giác ABCD có các cặp cạnh đối không song song và . Xác định giao tuyến của các cặp mặt phẳng sau đây:
a) và
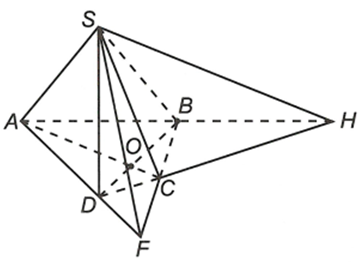
a) Trong mặt phẳng (ABCD) gọi
Ta có
Lại có
Từ (1) và (2) suy ra
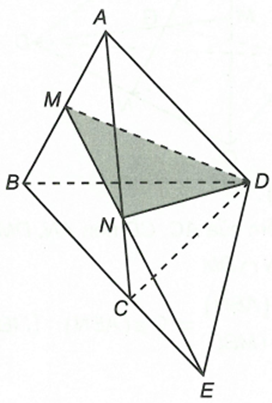
Câu 5:
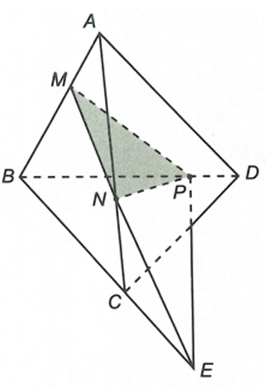
Trong mặt phẳng (ABC) gọi
Ta thấy
Lại có
Từ (1) và (2) suy ra
Câu 6:
Cho bốn điểm A, B, C, D không đồng phẳng. Trên hai đoạn thẳng AB, AC lần lượt lấy các điểm M, N sao cho và . Tìm giao tuyến của (DMN) và (BCD).
Trong tam giác có
Nên MN và BC không song song theo định lý Ta-lét.
Trong mặt phẳng (ABC) gọi
Ta thấy (1)
Lại có
Từ (1) và (2) suy ra
Câu 7:
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Tìm giao tuyến của mặt phẳng (ACD) và (GAB).
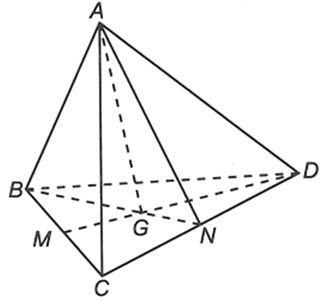
Ta có
Xét trong mặt phẳng (BCD) gọi
Vậy
Câu 8:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, CD. Tìm giao tuyến của hai mặt phẳng (MBD) và (ABN).
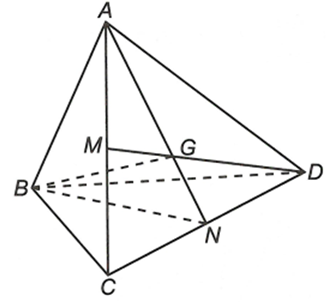
Ta có
Vì M, N lần lượt là trung điểm của AC, CD nên AN, DM là hai trung tuyến của tam giác ACD.
Gọi
. Vậy
Câu 9:
Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là đường thẳng
Đáp án C
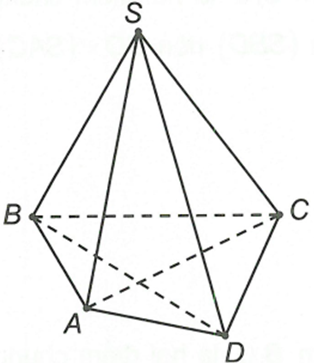
Ta có điểm S, B là hai điểm chung của hai mặt phẳng (SAB) và (SBC) nên
Câu 10:
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng
Đáp án C
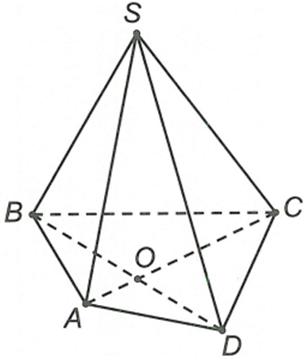
Ta có điểm S, C là hai điểm chung của hai mặt phẳng (SAO) và (SBC) nên
Câu 11:
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Giao tuyến của hai mặt phẳng (SAD) và (SBD) là đường thẳng
Đáp án D
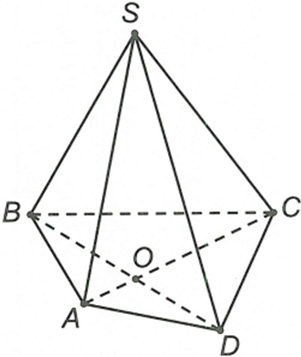
Ta có điểm S, O là hai điểm chung của hai mặt phẳng (SAO) và (SBD) nên
Câu 12:
Cho hình chóp S.ABC, gọi G là trọng tâm của tam giác ABC; M, N lần lượt là trung điềm BC, AC. Giao tuyến của (SAM) và (SBN) là
Đáp án A

Ta có điểm S, G là hai điểm chung của hai mặt phẳng (SAM) và (SBN) nên
Câu 13:
Cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O, giao tuyến của mặt (SAC) và (SBD) là
Đáp án D
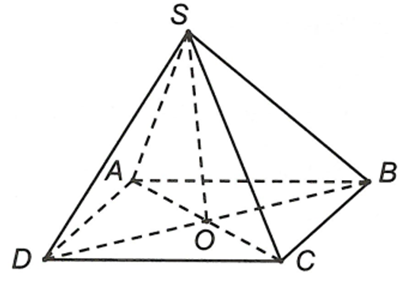
Ta có điểm S, O là hai điểm chung của hai mặt phẳng (SAC) và (SBD) nên
Câu 14:
Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của CD và AD, G là trọng tâm tam giác ACD. BG là giao tuyến của hai mặt phẳng nào?
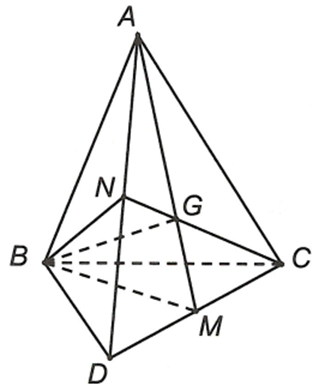
Câu 15:
Cho tứ diện ABCD, gọi N và K lần lượt là trung điềm của AD và BC. NK là giao tuyến của mặt phẳng (BCA/) với mặt phẳng nào
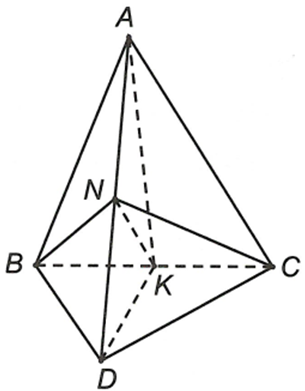
Câu 16:
Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của AD và BC. MN là giao tuyến của hai mặt phẳng nào?
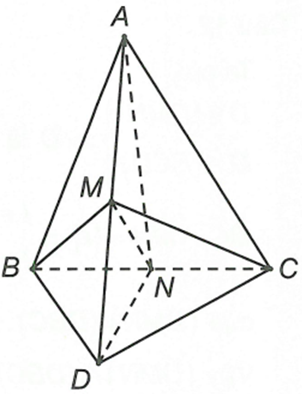
Ta có điểm M, N là hai điểm chung của hai mặt phẳng (BCM) và (AND) nên
Câu 17:
Cho hình chóp S.ABCD có đáy là hình bình hành. M, N lần lượt là trung điểm của BC và SD. Giao tuyến của hai mặt phẳng (AMN) và (SCD) là
Đáp án C
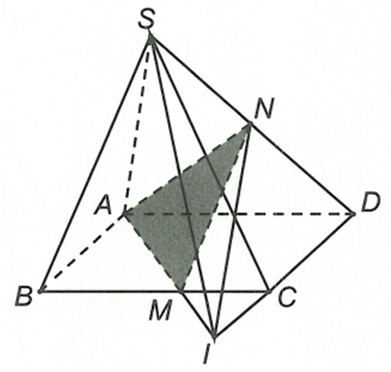
Câu 18:
Cho hình chóp S.ABCD với AC và BD giao nhau tại M, AB và CD giao nhau tại N. Hai mặt phẳng (SAB) và (SCD) có giao tuyến là
Đáp án C
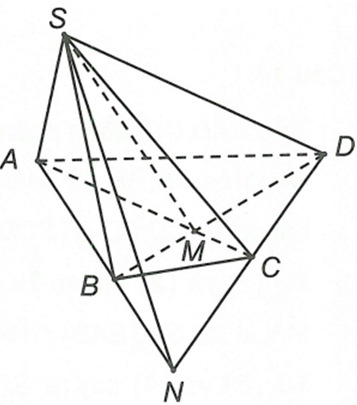
Ta có điểm S, N là hai điểm chung của hai mặt phẳng (SAB) và (SCO) nên
Câu 19:
Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC. Gọi K thuộc BD sao cho KD < KB. Gọi E là giao điểm của JK và CD, F là giao điểm của AD và IE. Giao tuyến của (IJK) và (ACD) là
Đáp án D
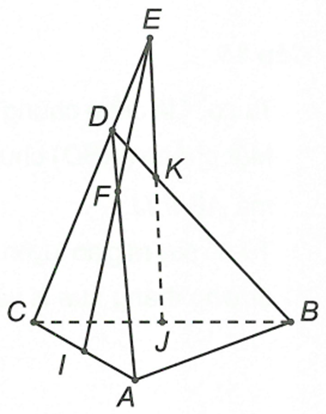
Gọi E là giao điểm của JK và CD
E là điểm chung thứ nhất
Lại có I là điểm chung thứ hai
Vậy
Câu 20:
Cho tứ diện ABCD. M, N là hai điểm lần lượt thuộc hai cạnh AB, AC sao cho MN cắt BC tại I. Khẳng định nào sau đây là đúng
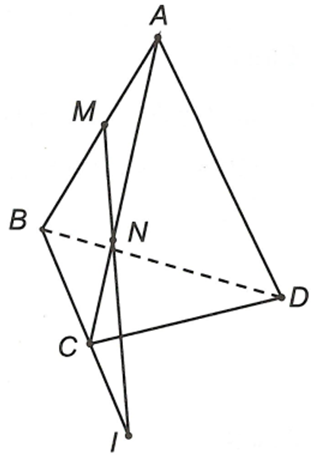
Ta có:
D là điểm chung của (DMN), (DBC)
I là điểm chung của (DMN), (DBC)
Vậy
Câu 21:
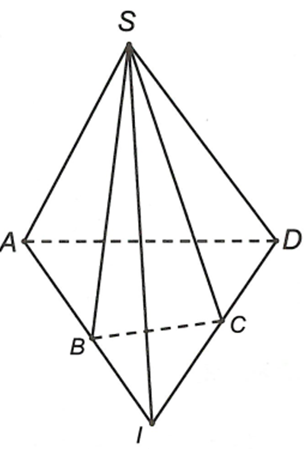
Vì AB, CD đồng phẳng nên gọi
Ta có
Lại có
Từ (1) và (2) suy ra (3)
Mặt khác (4)
Từ (3) và (4) suy ra
Câu 22:
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn). Gọi O là giao điểm của AC và BD, I là giao điểm của AB và CD. Giao tuyến của (SAB) và (SCO) là
Đáp án A
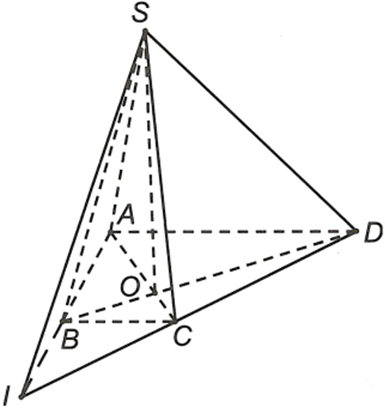
Ta có AB, CD đồng phẳng nên gọi
Ta có
Lại có
Từ (1) và (2) suy ra (3)
Mặt khác (4)
Từ (3) và (4) suy ra
Câu 23:
Cho tứ diện ABCD. Gọi I, J và K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là
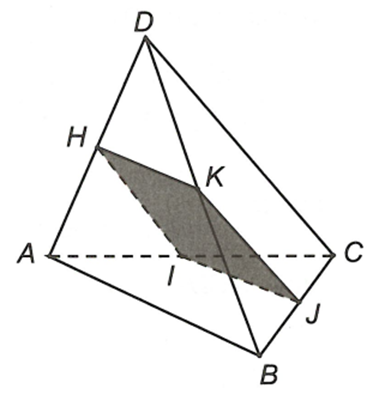
Ta có K là điểm chung của hai mặt phẳng (ABD) và (JJK)
Mặt phẳng (ABD) chứa AB, mặt phẳng (JJK) chứa IJ mà AB // IJ
Từ đó suy ra giao tuyến của hai mặt phẳng (ABD) và (IJK) là đường thẳng qua K và song song với AB
Câu 24:
Đáp án B
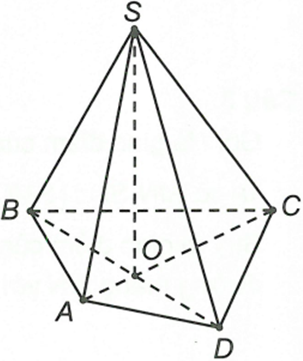
Ta có
Gọi O là giao điểm của AC và BD
Suy ra
Vậy
Câu 25:
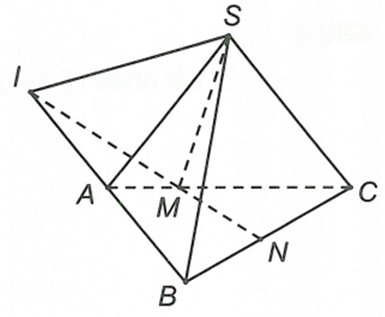
Ta có . Gọi I là giao điểm của MN với AB
Suy ra
Vậy
