Trắc nghiệm Hai đường thẳng vuông góc có đáp án (Nhận biết)
-
742 lượt thi
-
15 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây đúng?
Đáp án B
A sai vì: Nếu a và b cùng vuông góc với c thì a và b hoặc song song hoặc chéo nhau hoặc cắt nhau (cùng nằm trong mặt phẳng vuông góc với c)
C sai vì: Giả sử hai đường thẳng a và b chéo nhau, ta dựng đường thẳng c là đường vuông góc chung của a và b. Khi đó góc giữa a và c bằng với góc giữa b và c và cùng bằng , nhưng hiển nhiên hai đường thẳng a và b không song song.
D sai vì: Giả sử a vuông góc với c,b song song với c, khi đó góc giữa a và c bằng , còn góc giữa b và c bằng .
Do đó B đúng.
Câu 2:
Trong các mệnh đề dưới đây mệnh đề đúng là?
Đáp án A
Đáp án B sai vì vẫn có thể xảy ra các trường hợp hai đường thẳng đó chéo nhau, cắt nhau, trùng nhau hoặc thậm chí là vuông góc.
Do đó đáp án D cũng sai.
Đáp án C sai vì hai đường thẳng đó có thể chéo nhau.
Câu 3:
Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án D
Đáp án A sai vì nếu góc giữa hai véc tơ chỉ phương lớn hơn thì góc giữa hai đường thẳng sẽ là góc bù với góc đó chứ không bằng.
Đáp án B sai vì vẫn có thể xảy ra các trường hợp b và c chéo nhau, cắt nhau, trùng nhau.
Đáp án C sai vì góc giữa hai đường thẳng có thể nhọn hoặc vuông.
Do đó D đúng.
Câu 4:
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
Đáp án B
Đáp án A sai vì nếu đường thẳng đó cắt mặt phẳng chứa hai đường thẳng còn lại tại chính giao điểm của hai đường thẳng thì ba đường thẳng đó đồng quy.
Do đó đáp án C và D cũng sai.
Câu 5:
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:
Đáp án C
Gọi M là trung điểm của CD.
Suy ra ABCD nên số đo góc giữa hai đường thẳng AB và CD bằng
Câu 7:
Trong các khẳng định sau, khẳng định nào đúng?
Đáp án D
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia nên nếu a và b song song, nếu a vuông góc với c thì b cũng vuông góc với c
Câu 8:
Cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó a(P). Mệnh đề nào sau đây là sai?
Đáp án D
Dễ thấy các đáp án A, B, C đều đúng.
Đáp án D: Vì b có thể nằm trong mặt phẳng (P) nên D sai.
Câu 9:
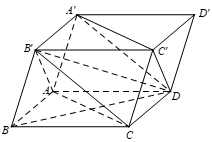
Cho hình hộp ABCD.A′B′C′D′. Giả sử tam giác AB′C và A′DC′ đều có 3 góc nhọn. Góc giữa hai đường thẳng AC và A′D là góc nào sau đây?
Đáp án D
Ta có: AC // A′C′ (tính chất của hình hộp)
⇒ (AC,A′D) = (A′C′,A′D) = (do giả thiết cho DA′C′ nhọn).
Câu 11:
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ và ?
Đáp án C

(ABCD là hình vuông).
Câu 12:
Cho tứ diện ABCD có AB = AC = AD và . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ và ?
Đáp án B
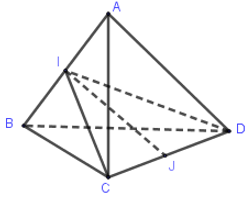
Ta có BAC và BAD là 2 tam giác đều, I là trung điểm của AB nên CI = DI (2 đường trung tuyến của 2 tam giác đều chung cạnh AB) nên CID là tam giác cân ở I.
Do đó IJCD
Câu 15:
Cho tứ diện ABCD có AB vuông góc với CD. Mặt phẳng (P) song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Tứ giác MNPQ là hình gì?
Đáp án C
Tương tự ta có: MN//CD, NP//AB, QP//CD
Do đó tứ giác MNPQ là hình bình hành
lại có MNMQ (do AB⊥CD)
Vậy tứ giác MNPQ là hình chữ nhật.
