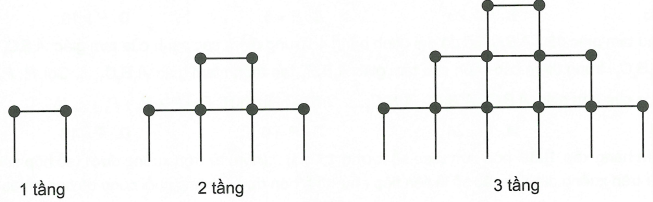
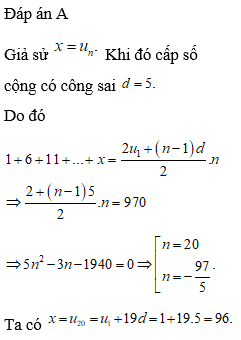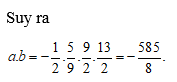Dựa vào tính chất của cấp số cộng: chứng minh đẳng thức, giải phương trình và các bài toán thực tế
-
937 lượt thi
-
25 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 3:
Với giá trị nào của x thì lập thành cấp số cộng?
Đáp án D
Để 3 số lập thành cấp số cộng thì
(phương trình vô nghiệm)
=> Không tìm được x thỏa yêu cầu.
Câu 4:
Đáp án D
Ta có nên đa giác có 4 cạnh.
Câu 5:
Đáp án B
Đặt phương trình (1) trở thành
Phương trình (1) có 4 nghiệm là 4 số hạng liên tiếp của một cấp số cộng khi và chỉ khi phương trình (2) có 2 nghiệm dương phân biệt thỏa mãn
Điều kiện phương trình (2) có 2 nghiệm dương phân biệt
Theo định lý Vi-ét
Từ (*) và (**) suy ra thế vào (***) ta được m=9 (nhận).Câu 8:
Cho tam giác vuông có độ dài ba cạnh lập thành một cấp số cộng với công sai d=2. Bán kính đường tròn ngoại tiếp R của tam giác đó là
Đáp án D
Gọi độ dài 3 cạnh của tam giác cần tìm là
Theo bài ra, ta có
Suy ra độ dài cạnh huyền là 6+4=10
Vậy R=5Câu 9:
Đáp án D
Theo giả thiết
Câu 12:
Đáp án B
Gọi góc nhỏ nhất là x, ta có bốn góc là (với d là công sai).
Ta có hệ
Giải hệ ta tìm được
Câu 13:
Đáp án C
Giả sử trồng được n hàng cây
Số cây ở mỗi hàng lập thành cấp số cộng có và công sai d=1
Theo giả thiết
Kết hợp với điều kiện, ta được n=80
Vậy có tất cả 80 hàng cây.
Câu 14:
Đáp án C
Giả sử đa giác có n cạnh; độ dài các cạnh thứ tự lập thành cấp số cộng với công sai d=3cm là
Từ giả thiết ta có
Câu 16:
Đáp án C
Ta có -2; 2x+1; 5 theo thứ tự lập thành một cấp số cộng nênCâu 17:
Đáp án C
Ta có
Khi đóCâu 20:
Đáp án B
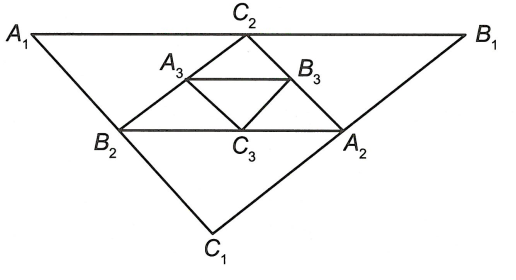
Ta có
VậyCâu 22:
Đáp án D
Khoảng cách từ các cây đến mốc 6 ki-lô-mét tạo thành cấp số cộng có công sai d=20m
Ta có
Cây cuối cùng ở vị trí 8 ki-lô-mét nên ta có
Câu 23:
Đáp án B
Quãng đường An đi được trong mỗi giờ là một cấp số cộng.
Ta có
Với n=27 thì nên vô lý.
Vậy An đi từ nhà về quê hết 4 giờ.
Câu 24:
Đáp án D
Số cốc nước bán được trong các ngày lập thành một cấp số cộng với công sai d=1.
Số cốc nước bán trong ngày thứ 10 là