22 câu hỏi trắc nghiệm thuộc Dạng 2: Tìm thiết diện nhờ quan hệ song song có đáp án

Câu 1:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc cạnh AC (không trùng với A hoặc C). Tìm thiết diện của (P) và hình chóp.

Xem đáp án

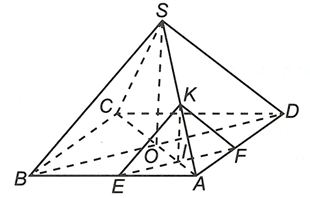
Gọi $\{O\} = A C \cap D B .$

Do SO nằm trong $(S B D)$ nên $S O // (α) .$

Mặt phẳng (SAC) chứa SO và có điểm chung với $(α)$ là I, do đó $(S A C) \cap (α) = I K$ với $I K // S O$ và $K \in S A .$

Tương tự $(S A B) \cap (α) = K E$ với $K E // S B$ và $E \in A B .$

$(S A D) \cap (α) = K F$ với $K F // S D$ và $F \in A D .$

Suy ra thiết diện của (P) với hình chóp S.ABCD là tam giác KEF.

Ta có $\frac{E F}{B D} = \frac{A E}{A B} = \frac{A F}{A D} = \frac{A K}{A S} = \frac{K E}{S B} = \frac{K F}{S D}$

$\Rightarrow Δ S B D$ đồng dạng với $Δ K E F .$

Tam giác SBD là tam giác đều nên $Δ K E F$ cũng là tam giác đều.

Vậy thiết diện của (P) và hình chóp S.ABCD là tam giác đều.

Câu 2:

Cho hình lăng trụ ABC.A'B'C'. Gọi I, J, K lần lượt là trọng tâm tam giác ABC, ACC', AB'C'. Chứng minh (IJK) // (BB'C)

Xem đáp án

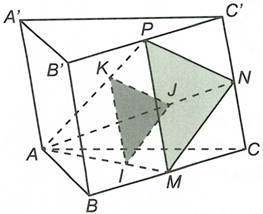
Gọi M, N, P lần lượt là trung điểm $B C; C C^{'}; B^{'} C^{'} .$

Do I, J, K lần lượt là trọng tâm tam giác $A B C, A C C^{'}$ nên $\frac{A I}{A M} = \frac{A J}{A N} = \frac{2}{3}$ nên $I J // M N \Rightarrow I J // (B C C^{'} B^{'}) .$

Tương tự $I K // (B C C^{'} B^{'}) \Rightarrow (I J K) // (B C C^{'} B^{'}) .$

Hay $(I J K) // (B B^{'} C) .$

Câu 3:

Cho hình chóp cụt tam giác ABC.A'B'C' có hai đáy là hai tam giác vuông tại A và A' và có $\frac{AB}{A^{'} B^{'}} = \frac{1}{2} .$ Khi đó tỉ số diện tích $\frac{S_{ΔABC}}{S_{{ΔA}^{'} B^{'} C^{'}}}$ bằng bao nhiêu?

Xem đáp án

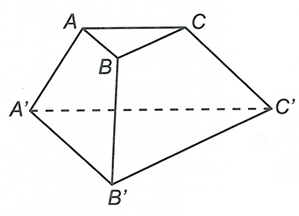
Cho hình chóp cụt tam giác ABC.A'B'C' có hai đáy là hai tam giác vuông tại A và A' và có AB/A'B' = 1/2 (ảnh 1)

Hai tam giác ABC và A'B'C' đồng dạng $\frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} = \frac{C A}{C^{'} A^{'}} = \frac{1}{2}$ nên $\frac{S_{Δ A B C}}{S_{Δ A^{'} B^{'} C^{'}}} = \frac{\frac{1}{2} A B . A C . \sin A}{\frac{1}{2} A^{'} B^{'} . A^{'} C^{'} . \sin A^{'}} = \frac{1}{4} .$

Cách khác: Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng nên $\frac{S_{Δ A B C}}{S_{Δ A^{'} B^{'} C^{'}}} = {(\frac{1}{2})}^{2} = \frac{1}{4} .$

Câu 4:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho

\frac{S M}{S A} = \frac{2}{3} .

Một mặt phẳng

(α)

đi qua M song song với AB và CD, cắt hình chóp theo một tứ giác. Tính diện tích tứ giác đó.

Xem đáp án

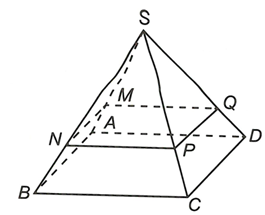
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho SM/SA = 2/3 (ảnh 1)

Qua M dựng đường thẳng song song AB cắt SB tại N.

Qua M dựng đường thẳng song song AD cắt SD tại Q.

Qua N dựng đường thẳng song song BC cắt SC tại P.

Ta có $\{\begin{cases} M N // A B \Rightarrow M N // (A B C D) \\ N P // B C \Rightarrow N P // (A B C D) \end{cases} \Rightarrow (M N P Q) // (A B C D) .$

Ta có tỉ lệ diện tích $\frac{S_{M N P Q}}{S_{A B C D}} = {(\frac{M N}{A B})}^{2} = {(\frac{S M}{S A})}^{2} = \frac{4}{9} .$

Lại có $S_{A B C D} = 10.10 = 100 \Leftrightarrow S_{M N P Q} = 100. \frac{4}{9} = \frac{400}{9} .$

Câu 5:

Cho hình chóp S.ABCD với ABCD là hình thoi cạnh a, SAD là tam giác đều. Gọi M là một điểm thuộc cạnh AB, AM = x, (P) là mặt phẳng qua M song song với (SAD). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).

Xem đáp án

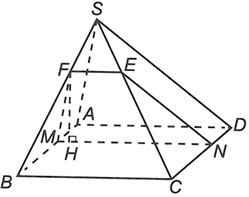
Cho hình chóp S.ABCD với ABCD là hình thoi cạnh a, SAD là tam giác đều. Gọi M là một điểm thuộc cạnh AB, AM = x, (P) là mặt phẳng qua M song song với (SAD) (ảnh 1)

Do $(P)$ đi qua M và song song với $(S A D)$ nên cắt các mặt của hình chóp bằng các giao tuyến đi qua M và song song với $(S A D)$ . Do ABCD là hình thoi và tam giác SAD đều. Nên thiết diện thu được là hình thang cân MNEF $(M N // E F; M F = E N) .$

Ta có $M N = a, \frac{E F}{B C} = \frac{S F}{S B} = \frac{M A}{A B} = \frac{x}{a} \Rightarrow E F = x; M F = a - x .$

Đường cao FH của hình thang cân bằng $F H = \sqrt{M F^{2} - {(\frac{M N - E F}{2})}^{2}} = \frac{\sqrt{3}}{2} (a - x) .$

Khi đó diện tích hình thang cân là $S = \frac{\sqrt{3}}{4} (a^{2} - x^{2})$

Câu 6:

Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sau đây sai?

A. $(A B B^{'} A^{'}) // (C D D^{'} C^{'}) .$

B. $(B D A^{'}) // (D^{'} B^{'} C) .$

C. $(B A^{'} D^{'}) // (A D C) .$

D. $(A C D^{'}) // (A^{'} C^{'} B) .$

Xem đáp án

Đáp án C

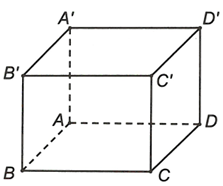
Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sau đây sai? (ảnh 1)

Ta có $(B A^{'} D^{'}) \equiv (B C D^{'} A^{'})$ và $(A D C) \equiv (A B C D) .$

Mà

(B C A^{'} D^{'}) \cap (A B C D) = B C,

suy ra

(B A^{'} D^{'}) // (A D C)

sai

Câu 7:

Mệnh đề nào sau đây sai?

A. (BA'C') // (ACD')

B. (ADD'A') // (BCC'B)

C. (BA'D) // (CB'D')

D. (ABA') // (CB'D')

Xem đáp án

Đáp án D

Mệnh đề nào sau đây sai? A. (BA'C') // (ACD') B. (ADD'A') // (BCC'B) C. (BA'D) // (CB'D') D. (ABA') // (CB'D') (ảnh 1)

Ta có $\{\begin{cases} B A^{'} // C D^{'} \\ A^{'} C^{'} // A C \end{cases} \Rightarrow (B A^{'} C^{'}) // (A C D^{'}) .$

$\{\begin{cases} A D // B C \\ A A^{'} // B B^{'} \end{cases} \Rightarrow (A D D^{'} A^{'}) // (B C C^{'} B^{'}) .$

$\{\begin{cases} B D // B^{'} D^{'} \\ A^{'} D // B^{'} C \end{cases} \Rightarrow (B A^{'} D) // (C B^{'} D^{'})$

Mặt khác $B^{'} \in (A B A^{'}) \cap (C B^{'} D^{'}) \Rightarrow$ D sai.

Câu 8:

Đặc điểm nào sau đây đúng với hình lăng trụ?

A. Hình lăng trụ có tất cả các mặt bên bằng nhau

B. Đáy của hình lăng trụ là hình bình hành

C. Hình lăng trụ có tất cả các mặt bên là hình bình hành

D. Hình lăng trụ có tất cả các mặt là hình bình hành

Xem đáp án

Đáp án C

Ta có thể lấy hình lăng trụ có đáy là tam giác thường sẽ thấy các câu còn lại sai.

Câu 9:

Trong hình hộp (hoặc lăng trụ, hoặc hình chóp cụt) đoạn thẳng nối hai đỉnh mà hai đỉnh đó không cùng nằm trên một mặt nào của hình hộp (hoặc hình lăng trụ, hoặc hình chóp cụt), được gọi là đường chéo của nó. Tìm mệnh đề đúng.

A. Hình lăng trụ tứ giác có các đường chéo đồng quy

B. Hình lăng trụ có các đường chéo đường chéo đồng quy

C. Hình chóp cụt có các đường chéo đồng quy

D. Hình hộp có các đường chéo đồng quy

Xem đáp án

Đáp án D

Vì trong hình hộp cứ hai đường chéo đồng phẳng tạo nên hình bình hành, nên chúng luôn cắt nhau tại trung điểm của mỗi đường.

Câu 10:

Cho hình chóp S.ABCD với đáy ABCD là hình bình hành. Gọi I, J, K, L lần lượt là trung điểm của SA, SB, SC, SD. Mệnh đề nào sau đây đúng?

A. $(I J K) // (B C D) .$

B. $S A // (I K L) .$

C. $I K \subset (S B C) .$

D. $J L // S C .$

Xem đáp án

Đáp án A

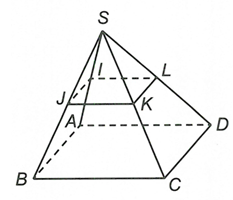
Cho hình chóp S.ABCD với đáy ABCD là hình bình hành. Gọi I, J, K, L lần lượt là trung điểm của SA, SB, SC, SD. (ảnh 1)

Ta có: $\{\begin{cases} I K // A C \\ I J // A B \end{cases} \Rightarrow (I J K) // (B C D) .$

Câu 11:

Cho hình hộp ABCD.A'B'C'D' (các đỉnh lấy theo thứ tự đó), AC cắt BD tại O còn A'C' cắt B'D' tại O'. Khi đó (AB'D') sẽ song song với mặt phẳng nào dưới đây?

A. $(A^{'} O C^{'}) .$

B. $(B D A^{'}) .$

C. $(B D C^{'}) .$

D. $(B C D) .$

Xem đáp án

Đáp án C

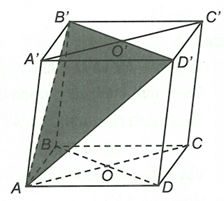
Cho hình hộp ABCD.A'B'C'D' (các đỉnh lấy theo thứ tự đó), AC cắt BD tại O còn A'C' cắt B'D' tại O'. Khi đó (AB'D') sẽ song song với mặt phẳng nào dưới đây? (ảnh 1)

Ta có: $\{\begin{cases} B D // B^{'} D^{'} \subset (A B^{'} D^{'}) \\ D C^{'} // A B^{'} \subset (A B^{'} D^{'}) \\ B D \cap D C^{'} = \{D\} \end{cases}$ nên $(A B^{'} D^{'}) // (B D C^{'}) .$

Câu 12:

Cho hình lập phương ABCD.A'B'C'D'. gọi I là trung điểm của A'B'. Mặt phẳng (IBD) cắt hình hộp theo thiết diện là hình gì?

A. Hình chữ nhật

B. Hình thang

C. Hình bình hành

D. Tam giác

Xem đáp án

Đáp án B

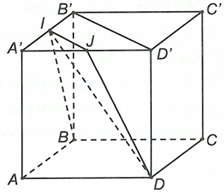
Cho hình lập phương ABCD.A'B'C'D'. gọi I là trung điểm của A'B'. Mặt phẳng (IBD) cắt hình hộp theo thiết diện là hình gì? (ảnh 1)

Gọi $\{J\} = A^{'} D^{'} \cap (I B D) .$

Ta có thiết diện của mặt phẳng $(I B D)$ và hình hộp là tứ giác IJDB.

Mặt khác $\{\begin{cases} (A B C D) // (A^{'} B^{'} C^{'} D^{'}) \\ (I B D) \cap (A^{'} B^{'} C^{'} D^{'}) = I J \Rightarrow I J // B D \\ (I B D) \cap (A B C D) = B D \end{cases}$

=> IJDB là hình thang.

Câu 13:

Cho hình hộp ABCD.EFGH, gọi I, J lần lượt là tâm của hình bình hành ABCD và EFGH. Khẳng định nào sau đây là sai?

A. $(A B C D) // (E F G H) .$

B. $(A B F E) // (D C G H) .$

C. $(A C G E) // (B D H F) .$

D. $(A B J) // (G H I) .$

Xem đáp án

Đáp án C

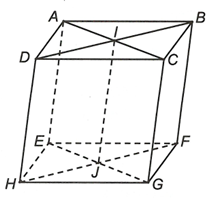
Cho hình hộp ABCD.EFGH, gọi I, J lần lượt là tâm của hình bình hành ABCD và EFGH. Khẳng định nào sau đây là sai? (ảnh 1)

Ta có $A C \cap B D = \{I\}$ và $E G \cap H F = \{J\}$ nên $(A C G E) \cap (B D H F) = I J .$

Nên C sai.

Câu 14:

Phát biểu nào dưới đây là định lý Ta-lét trong không gian?

A. Ba mặt phẳng song song chắn trên hai cát tuyến song song các đoạn thẳng tương ứng tỉ lệ.

B. Ba mặt phẳng song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng bằng nhau.

C. Ba mặt phẳng song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ.

D. Ba mặt phẳng song song chắn trên hai cát tuyến song song các đoạn thẳng tương ứng bằng nhau.

Xem đáp án

Đáp án C

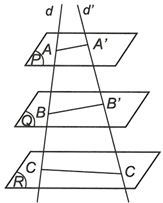
Phát biểu nào dưới đây là định lý Ta-lét trong không gian? (ảnh 1)

Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.

Câu 15:

Cho hình lăng trụ ABC.A'B'C', gọi M, N theo thứ tự là trọng tâm của các tam giác ABC và A'B'C'. Thiết diện tạo bởi mặt phẳng (AMN) với hình lăng trụ đã cho là

A. hình bình hành

B. hình tam giác vuông

C. hình thang

D. hình tam giác cân

Xem đáp án

Đáp án A

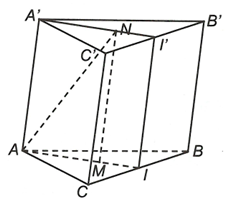
Cho hình lăng trụ ABC.A'B'C', gọi M, N theo thứ tự là trọng tâm của các tam giác ABC và A'B'C'. Thiết diện tạo bởi mặt phẳng (AMN) với hình lăng trụ đã cho là (ảnh 1)

Ta có $N \in A^{'} I^{'}$ và $M \in A I$ ( $A^{'} I^{'}$ là trung tuyến của $Δ A^{'} B^{'} C^{'}$ và AI là trung tuyến của $Δ A B C$ )

Do đó mp (AMN) cũng chính là mp (A'I'IA)

Ta có $(A A^{'} I^{'} I) \cap (A^{'} B^{'} C^{'}) = A^{'} I^{'}; (A A^{'} I^{'} I) \cap (A B C) = A I;$

$(A A^{'} I^{'} I) \cap (B C C^{'} B^{'}) = I I^{'} .$

Vậy thiết diện tạo với mp (A'I'IA) và hình lăng trụ là tứ giác AA'I'I

Mặt khác II' // CC' (đường trung bình trong hình bình hành CC'B'B) và CC' // AA' (tính chất hình lăng trụ).

Do đó II' // AA'

II' = CC' (đường trung bình trong hình bình hành CC'B'B )

và CC' = AA' (tính chất lăng trụ). Do đó II' = AA'

Vậy tứ giác AA'I'I là hình bình hành.

Câu 16:

Cho hình lập phương ABCD.A'B'C'D', gọi M, N, P lần lượt là trung điểm của các cạnh AB, B'C', DD' Khẳng định nào sau đây sai?

A. mp

(M N P)

không song song với mp

(B D C^{'})

B. mp

(M N P)

cắt lập phương theo thiết diện là một lục giác

A B C D . A^{'} B^{'} C^{'} D^{'}

C. mp

(M N P)

đi qua tâm của hình lập phương

D. mp

(M N P)

đi qua trung điểm của cạnh BB'

Xem đáp án

Đáp án A

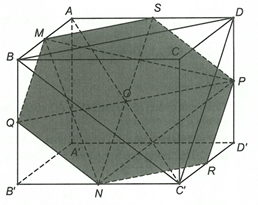
Cho hình lập phương ABCD.A'B'C'D', gọi M, N, P lần lượt là trung điểm của các cạnh AB, B'C', DD' Khẳng định nào sau đây sai? (ảnh 1)

Gọi S, R, Q lần lượt là trung điểm của AD, $C^{'} D^{'}, B B^{'} .$

Dễ thấy, $M S // N R;$

$P S // Q N;$

$M Q // P R .$

=> M, S, P, R, N, Q đồng phẳng.

Lại có $M S // B D \Rightarrow M S // (B D C^{'});$

$P S // N Q // B C^{'} \Rightarrow P S // (B D C^{'}) .$

Vậy

(M N P) // (B D C^{'}) .

Câu 17:

Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Mặt phẳng

(α)

đi qua M song song với

(S B C)

cắt hình chóp S.ABCD theo thiết diện là

A. hình bình hành

B. hình vuông

C. hình tam giác

D. hình thang

Xem đáp án

Đáp án D

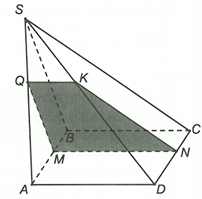
Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. (ảnh 1)

Gọi $M N = (α) \cap (A B C D)$ với $N \in C D,$ ta có

$\{\begin{cases} (α) // (S B C) \\ (S B C) \cap (A B C D) = B C \end{cases} \Rightarrow M N // B C .$

Gọi $N K = (α) \cap (S C D)$ với $K \in S D,$ ta có

$\{\begin{cases} (α) // (S B C) \\ (S B C) \cap (S C D) = S C \end{cases} \Rightarrow K N // S C .$

Do $M N // B C // A D$ nên $M N // (S A D) .$

Gọi $K Q = (α) \cap (S A B)$ với $Q \in S A,$ ta có $K Q // A D .$

Vậy thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng $(α)$ là hình thang MNKQ có đáy MN và QK.

Câu 18:

Cho hình chóp S.ABC có đáy ABC thỏa mãn AB = AC = 4, $\hat{B A C} = 30 ° .$ Mặt phẳng (P) song song với (ABC) cắt SA tại M sao cho SM = 2MA. Diện tích thiết diện của (P) và hình chóp S.ABC bằng bao nhiêu?

A. $\frac{16}{9} .$

B. $\frac{25}{9} .$

C. $\frac{14}{9} .$

D. 1.

Xem đáp án

Đáp án A

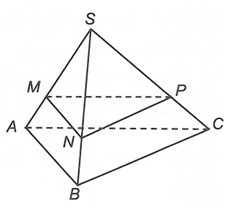
Cho hình chóp S.ABC có đáy ABC thỏa mãn AB = AC = 4, góc BAC = 30 độ. Mặt phẳng (P) song song với (ABC) cắt SA tại M sao cho SM = 2MA. (ảnh 1)

Đường thẳng qua M song song với AB cắt SB tại N.

Đường thẳng qua N song song với BC cắt SC tại P.

Ta có $\{\begin{cases} M N // A B \Rightarrow M N // (A B C) \\ M P // A C \Rightarrow M P // (A B C) \end{cases} \Rightarrow (M N P) // (A B C) .$

Gọi $h_{1}$ là đường cao của $Δ M N P$ ứng với đáy MN.

Gọi $h_{2}$ là đường cao của $Δ A B C$ ứng với đáy AB.

Dễ thấy $Δ M N P$ đồng dạng $Δ A B C$ ta có $\frac{M N}{A B} = \frac{h_{1}}{h_{2}} = \frac{S M}{S A} = \frac{2}{3} .$

Ta có $\frac{S_{Δ M N P}}{S_{Δ A B C}} = \frac{\frac{1}{2} h_{1} . M N}{\frac{1}{2} h_{2} . A B} = \frac{2}{3} . \frac{2}{3} = \frac{4}{9} .$

Lại có $S_{Δ A B C} = \frac{1}{2} A B . A C . \sin \hat{B A C} = \frac{1}{2} .4.4. \sin 30 ° = 4$

$\Rightarrow S_{Δ M N P} = S_{Δ A B C} . \frac{4}{9} = 4. \frac{4}{9} = \frac{16}{9} .$

Câu 19:

Cho hình chóp S.ABCD có đáy C là hình thang cân với cạnh bên $B C = 2,$ hai đáy $A B = 6, C D = 4.$ Mặt phẳng $(P)$ song song với $(A B C D)$ và cắt cạnh SA tại M sao cho $S A = 3 S M .$ Diện tích thiết diện của $(P)$ và hình chóp S.ABCD bằng bao nhiêu?

A. $\frac{2 \sqrt{3}}{3} .$

B. $\frac{7 \sqrt{3}}{9} .$

C. 2.

D. $\frac{5 \sqrt{3}}{9} .$

Xem đáp án

Đáp án D

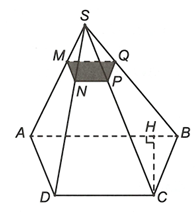
Cho hình chóp S.ABCD có đáy C là hình thang cân với cạnh bên BC = 2, hai đáy AB = 6, CD = 4 (ảnh 1)

Trong mặt phẳng $(S A D)$ kẻ $M N // A D, (S D C)$ kẻ $N P // D C, (S B C)$ kẻ $P Q // B C .$

Suy ra thiết diện của $(P)$ và hình chóp S.ABCD là tứ giác MNPQ.

Gọi CH là đường cao trong hình thang ABCD ta có $C H = \sqrt{2^{2} - 1^{2}} = \sqrt{3} .$

Suy ra $S_{A B C D} = \frac{(A B + D C)}{2} C H = \frac{(4 + 6)}{2} . \sqrt{3} = 5 \sqrt{3} .$

Do MNPQ đồng dạng với ABCD theo tỷ số $k = \frac{1}{3}$ nên $S_{M N P Q} = \frac{5 \sqrt{3}}{3^{2}} = \frac{5 \sqrt{3}}{9} .$

Câu 20:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, AB = 8, SA = SB = 6. Gọi (P) là mặt phẳng đi qua O và song song với (SAB). Tính diện tích thiết diện của (P) và hình chóp S.ABCD.

A. 12.

B. $6 \sqrt{5} .$

C. $5 \sqrt{5} .$

D. 13.

Xem đáp án

Đáp án B

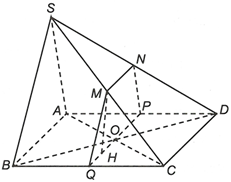
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, AB = 8, SA = SB= 6. Gọi (P) là mặt phẳng đi qua O và song song với (SAB) (ảnh 1)

Qua O dựng đường thẳng PQ // AB

Vậy P, Q lần lượt là trung điểm của AD và BC.

Qua P dựng đường thẳng PN // SA

Vậy N là trung điểm của SD.

Qua Q dựng đường thẳng QM // SB

Vậy M là trung điểm của SC. Nối M và N

=> thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.

Vì $P Q // C D; M N // C D \Rightarrow P Q // M N .$

Vậy tứ giác MNPQ là hình thang.

Ta có $PQ = AB = 8; MN = \frac{1}{2} AB = 4; MQ = NP = \frac{1}{2} SA = 3.$

Vậy MNPQ là hình thang cân.

Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ.

Khi đó ta có $HQ = \frac{1}{4} PQ = 2 \Rightarrow MH = \sqrt{{MQ}^{2} - {HQ}^{2}} = \sqrt{5} .$

Vậy diện tích của thiết diện cần tìm là $S = \frac{(MN + PQ) . MH}{2} = 6 \sqrt{5} .$

Câu 21:

Cho hình chóp S.ABC có M là điểm di động trên cạnh SA sao cho

\frac{S M}{S A} = k (k \in ℝ, 0 < k < 1) .

Gọi

(α)

là mặt phẳng đi qua M và song song với mặt phẳng

(A B C)

. Tìm k để mặt phẳng

(α)

cắt hình chóp S.ABC theo một thiết diện có diện tích bằng một nửa diện tích tam giác ABC.

A. $k = \frac{\sqrt{2}}{2} .$

B. $k = \frac{1}{3} .$

C. $k = \frac{\sqrt{3}}{2} .$

D. $k = \frac{1}{2} .$

Xem đáp án

Đáp án A

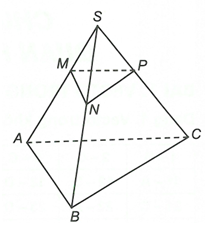
Cho hình chóp S.ABC có M là điểm di động trên cạnh SA sao cho SM/SA = k (k thuộc R, 0 < k < 1) (ảnh 1)

Gọi N, P là hai điểm lần lượt thuộc SB, SC thỏa mãn $M N // A B, M P // A C .$

Ta có $\{\begin{cases} M N // A B \Rightarrow M N // (A B C) \\ M P // A C \Rightarrow M P // (A B C) \end{cases} \Rightarrow (M N P) // (A B C) .$

Gọi $h_{1}$ là đường cao của $Δ M N P$ ứng với đáy MN.

Gọi $h_{2}$ là đường cao của $Δ A B C$ ứng với đáy AB.

Dễ thấy $Δ M N P$ đồng dạng $Δ A B C$ ta có $\frac{M N}{A B} = \frac{h_{1}}{h_{2}} = k .$

Vậy để thỏa mãn yêu cầu bài toán

$\frac{S_{Δ M N P}}{S_{Δ A B C}} = \frac{\frac{1}{2} h_{1} . M N}{\frac{1}{2} h_{2} . A B} = \frac{1}{2} \Leftrightarrow k . k = \frac{1}{2} \Leftrightarrow k = \frac{\sqrt{2}}{2} .$

Câu 22:

Cho hình hộp

A B C D . A^{'} B^{'} C^{'} D^{'}

có tất cả các mặt bên đều là hình vuông cạnh a. Các điểm M, N lần lượt trên AD', BD sao cho

A M = D N = x (0 < x < a \sqrt{2}) .

Khi đó với mọi giá trị x thì đường thẳng MN song song với mặt phẳng nào sau đây?

A. $(A D^{'} C^{'} B) .$

B. $(A^{'} D C^{'} B) .$

C. $(A^{'} D^{'} C B) .$

D. $(A D C^{'} B^{'}) .$

Xem đáp án

Đáp án C

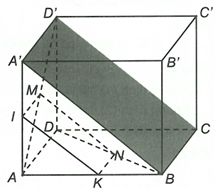
Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt bên đều là hình vuông cạnh a. Các điểm M, N lần lượt trên AD', BD sao cho AM = DN = x (ảnh 1)

Do tất cả các mặt bên đều là hình vuông cạnh a nên theo tính chất hình hộp ta có ABCD cũng là hình vuông cạnh a. Suy ra $B D = A D^{'} = a \sqrt{2} .$

Qua N kẻ $N K // A D$ với $K \in A B .$ Qua M kẻ $M I // A^{'} D^{'}$ với $I \in A A^{'} .$

Ta có $\frac{B K}{B A} = \frac{B N}{B D} \Leftrightarrow \frac{B A - K A}{B A} = \frac{B D - N D}{B D} \Leftrightarrow \frac{K A}{B A} = \frac{N D}{B D} .$

Mà $\frac{N D}{B D} = \frac{A M}{A D^{'}} = \frac{A I}{A A^{'}} .$ Do đó $\frac{A I}{A A^{'}} = \frac{A K}{A B} \Rightarrow I K // A^{'} B .$

Ta có $I \in (M N K)$ do $I M // K N // A D .$ Suy ra $M N \subset (M N I K) // (A^{'} D^{'} C B) .$

Vậy MN song song với mặt phẳng $(A^{'} D^{'} C B)$ với mọi $0 < x < a \sqrt{2} .$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập chuyên đề toán 11 Bài 4: Mặt phẳng song song với mặt phẳng có đáp án

Dạng 2: Tìm thiết diện nhờ quan hệ song song có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương