Đề thi Toán 11 Học kì 2 có đáp án (Đề 6)
-
2526 lượt thi
-
23 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 5x + 1}}{{1 + 3x - {x^2}}}\) bằng:
Hướng dẫn giải
Đáp án đúng là: C
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 5x + 1}}{{1 + 3x - {x^2}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {2 - \frac{5}{x} + \frac{1}{{{x^2}}}} \right)}}{{{x^2}\left( {\frac{1}{{{x^2}}} - \frac{3}{x} - 1} \right)}} = - 2.\)
Câu 2:
Hướng dẫn giải
Đáp án đúng là: C
Ta có y' = (cosx)' = −sinx.
Câu 3:
\(\mathop {\lim }\limits_{x \to 2} \left( { - 3{x^2} + 6x + 1} \right)\) bằng:
Hướng dẫn giải
Đáp án đúng là: B
Ta có \(\mathop {\lim }\limits_{x \to 2} \left( { - 3{x^2} + 6x + 1} \right) = - {3.2^2} + 6.2 + 1 = 1.\)
Câu 4:
Cho hàm số f(x) = 2x3 – 8. Giá trị f '(−2) bằng:
Hướng dẫn giải
Đáp án đúng là: A
Ta có f '(x) = 6x2 Þ f '(−2) = 24.
Câu 5:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC) và SA = a. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Hướng dẫn giải
Đáp án đúng là: D
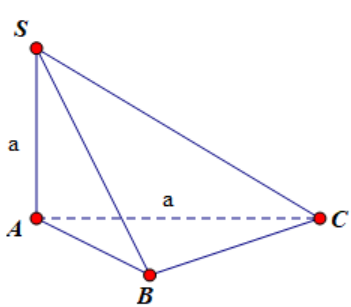
Ta có SA ^ (ABC) Þ AC là hình chiếu của SC lên (ABC)
Þ [SC,(ABC)] = \(\widehat {SCA}.\)
Tan\(\widehat {SCA}\)= \(\frac{{SA}}{{AC}} = \frac{a}{a} = 1 \Rightarrow \widehat {SCA} = 45^\circ \).
Câu 6:
Hướng dẫn giải
Đáp án đúng là: B
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left( { - {x^4} + 5{x^2} - 3} \right) = \mathop {\lim }\limits_{x \to + \infty } {x^4}\left( { - 1 + \frac{5}{{{x^2}}} - \frac{3}{{{x^4}}}} \right) = - \infty .\)
Câu 7:
Hàm số y = \(\frac{{3x - 1}}{{x + 1}}\) có đạo hàm là y' = \(\frac{m}{{{{(x + 1)}^2}}}\), giá trị của P = 2m – 1 là:
Hướng dẫn giải
Đáp án đúng là: A
Ta có y = \(\frac{{3x - 1}}{{x + 1}}\) Þ y' = \(\frac{4}{{{{(x + 1)}^2}}}\)Þ m = 4
Þ P = 2.4 – 1 = 7.
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và có cạnh SA vuông góc với mặt phẳng (ABCD). Trong các khẳng định sau, khẳng định nào sai?
Hướng dẫn giải
Đáp án đúng là: D
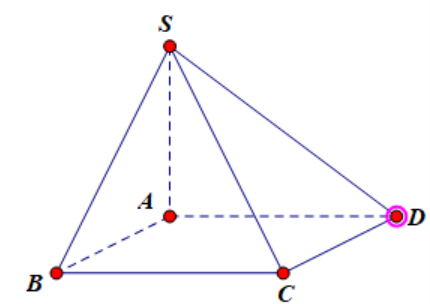
Ta có:
∙ SA ^ AB, SA ^ AC Þ SA ^ (ABC);
∙ BC ^ AB, BC ^ SA Þ BC ^ (SAB);
∙ BD ^ AC, BD ^ SA Þ BC ^ (SAC).
Vậy đáp án D sai.
Câu 9:
Phương trình tiếp tuyến của đồ thị hàm số y = x4 – 3x2 + 1 tại điểm M(1;−1) là:
Hướng dẫn giải
Đáp án đúng là: C
Ta có y = x4 – 3x2 + 1 Þ y' = 4x3 – 6x Þ y'(1) = −2.
Phương trình tiếp tuyến của đồ thị hàm số tại điểm M(1;−1) là:
y = −2(x – 1) – 1 = −2x + 1.
Câu 10:
Hướng dẫn giải
Đáp án đúng là: A
Ta có\(\mathop {\lim }\limits_{x \to {{( - 2)}^ - }} \frac{{5 - 3x}}{{x + 2}} = \frac{{5 - 3.( - 2)}}{{ - 2 + 2}} = \frac{{11}}{{{0^ - }}} = + \infty \)
Câu 11:
Phát biểu nào sau đây là đúng?
Hướng dẫn giải
Đáp án đúng là: A
Ta có (sin3x)' = (3x)'.cos3x = 3.cos3x
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và có SA = SC, SB = SD. Trong các khẳng định sau, khẳng định nào đúng?
Hướng dẫn giải
Đáp án đúng là: B
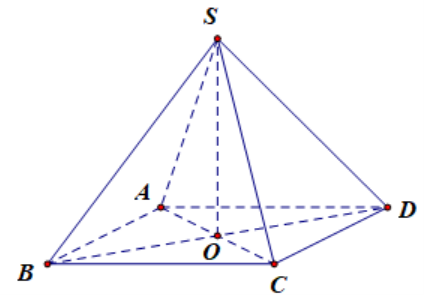
Ta có
∙ SA = SC Þ Tam giác SAC cân tại S
Þ SO là đường cao tam giác SAC Þ SO ^ AC (1)
∙ SB = SD Þ Tam giác SBD cân tại S
Þ SO là đường cao tam giác SBD Þ SO ^ BD (2)
Từ (1) và (2) suy ra SO ^ (ABCD).
Câu 13:
Cho hàm số . Hàm số đã cho liên tục tại x = 2 khi a bằng:
Hướng dẫn giải
Đáp án đúng là: A
Ta có: f(2) = m
\[\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f(x) = \mathop {\lim }\limits_{x \to 2} \frac{{3 - \sqrt {4x + 1} }}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \frac{{9 - (4x + 1)}}{{(x - 2)\left( {3 + \sqrt {4x + 1} } \right)}}\\ = \mathop {\lim }\limits_{x \to 2} \frac{{ - 4(x - 2)}}{{(x - 2)\left( {3 + \sqrt {4x + 1} } \right)}}\\ = \mathop {\lim }\limits_{x \to 2} \frac{{ - 4}}{{\left( {3 + \sqrt {4x + 1} } \right)}} = \frac{{ - 2}}{3}\end{array}\]
Để hàm số liên tục tại x = 2 thì f(2) = \(\mathop {\lim }\limits_{x \to 2} f(x)\) Û m = \( - \frac{2}{3}\).
Câu 14:
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} - 4x + 7} - 2x} \right)\) bằng:
Hướng dẫn giải
Đáp án đúng là: C
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} - 4x + 7} - 2x} \right)\)
= \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} - 4x + 7} } \right) - 2\mathop {\lim }\limits_{x \to + \infty } x\)
= \(\mathop {\lim }\limits_{x \to + \infty } x\left( {\sqrt {4 - \frac{4}{x} + \frac{7}{{{x^2}}}} } \right) - 2\mathop {\lim }\limits_{x \to + \infty } \)= +¥ − 2¥ = −1.
Câu 15:
Đường thẳng y = ax + b tiếp xúc với đồ thị hàm số y = x3 – 3x – 1 tại điểm có hoành độ bằng 2, giá trị của a + b bằng:
Hướng dẫn giải
Đáp án đúng là: B
Ta có y' = 3x2 – 3 Þ y'(2) = 9 và y = 1
Phương trình tiếp tuyến tại x = 2 là: y = 9(x – 2) + 1 = 9x – 17.
Þ a = 9, b = −17 Þ a + b = −8.
Câu 16:
Hướng dẫn giải
Đáp án đúng là: D
Ta có v = S' = 8t3 – 18t Þ v(2) = 28 (m/s).
Câu 17:
Hướng dẫn giải
Tại x0 = 2, ta có: f(2) = 5.2 – 3 = 7.
\(\mathop {\lim }\limits_{x \to 2} f(x) = \mathop {\lim }\limits_{x \to 2} \frac{{2{x^2} - x - 6}}{{x - 2}}\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{2(x - 2)\left( {x + \frac{3}{2}} \right)}}{{x - 2}}\)
\( = \mathop {\lim }\limits_{x \to 2} (2x + 3) = 7\)
Vì f(2) = \(\mathop {\lim }\limits_{x \to 2} f(x)\)= 7 nên hàm số đã cho liên tục tại x0 = 2.
Câu 18:
Hướng dẫn giải
Đặt f(x) = 2x4 – 3x3 – 5, f(x) là hàm đa thức nên liên tục trên ℝ.
Do đó f(x) liên tục trên đoạn [1;2]
f(1) = −6, f(2) = 3 Þ f(1).f(2) = −18 < 0
Þ phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng [1; 2].
Vậy phương trình đã cho có ít nhất một nghiệm.
Câu 19:
Hướng dẫn giải
Ta có y = \(\frac{1}{3}\)x3 + 2x2 – \(\frac{2}{3}\) Þ y' = x2 + 4x
Vì tiếp tuyến song song với đường thẳng d: y = −4x + 2022 nên y'(x0) = −4
Ta có x02 + 4x0 = −4 Û x02 + 4x0 + 4 = 0 Û x0 = -2 Þ y0 = \(\frac{{14}}{3}\).
y'(−2) = −4
Phương trình tiếp tuyến có dạng: y = y'(x0)(x – x0) + y0
Þ Phương trình tiếp tuyến y = −4(x + 2) + \(\frac{{14}}{3}\) = −4x − \(\frac{{10}}{3}\).
Câu 20:
Hướng dẫn giải
f '(x) = (x2 – 2x)'. (x – 3) + (x – 3)'. (x2 – 2x)
= (2x – 2).(x – 3) + (x2 – 2x) = 3x2 – 10x + 6
f '(x) > −1 Û 3x2 – 10x + 6 > −1 Û 3x2 – 10x + 7 > 0
Tập nghiệm của bất phương trình là : S = (−¥;1) È \(\left( {\frac{7}{3}; + \infty } \right)\).
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với cạnh AB = \(a\sqrt 2 \), SA vuông góc với mặt phẳng đáy và SA = 3a.
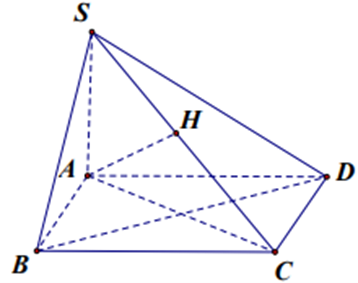
Chứng minh CD ^ (SAD).
Hướng dẫn giải
Ta có SA ^ (ABCD) mà CD Ì (ABCD) Þ SA ^ CD (1)
ABCD là hình vuông Þ CD ^ AD (2)
Từ (1) và (2) Þ CD ^ (SAD)
Câu 22:
Hướng dẫn giải
Ta có AC là hình chiếu vuông góc của SC trên mặt phẳng (ABCD) Þ \(\widehat {SCA}\) là góc giữa SC và mặt phẳng (ABCD)
Ta có AC = 2a (đường chéo hình vuông ABCD)
Tan \(\widehat {SCA}\)= \(\frac{{SA}}{{AC}} = \frac{{3a}}{{2a}} = \frac{3}{2}\) Þ \(\widehat {SCA}\)= 56°18’
Câu 23:
Hướng dẫn giải:
Ta có: \(\left. {\begin{array}{*{20}{c}}{BD \bot AC}\\{BD \bot SA}\end{array}} \right\}\)Þ BD ^ (SAC) mà AH Ì (SAC) Þ AH ^ BD.
Ta lại có: ∆SAC vuông tại A Þ AH = \(\frac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{6a\sqrt {13} }}{{13}}\).
