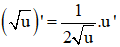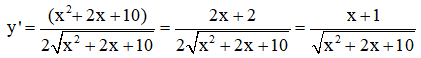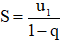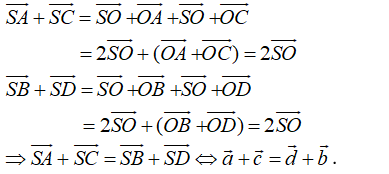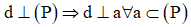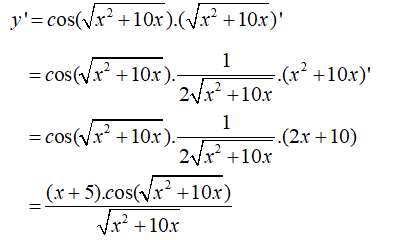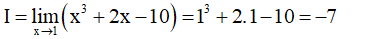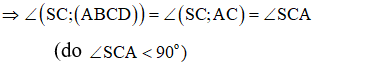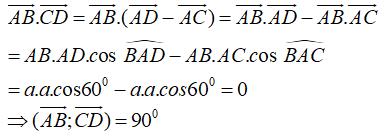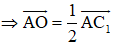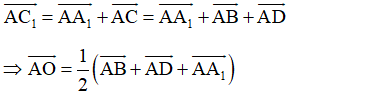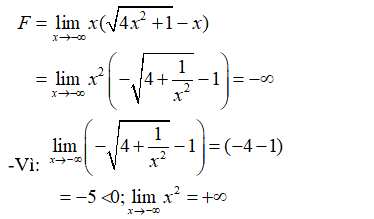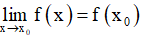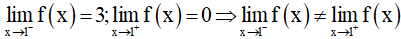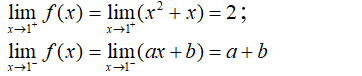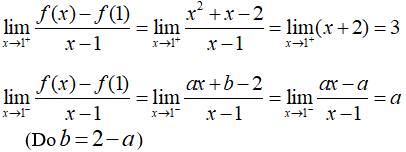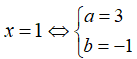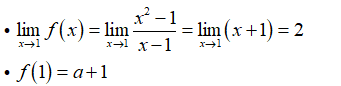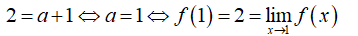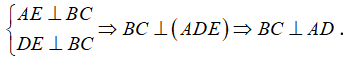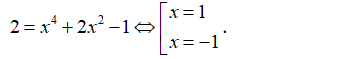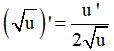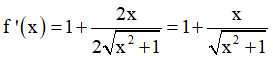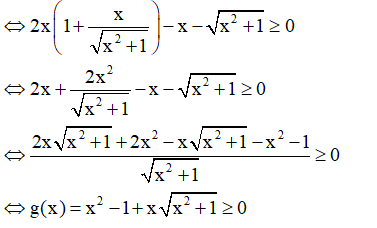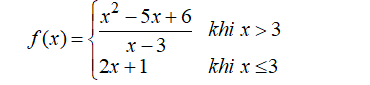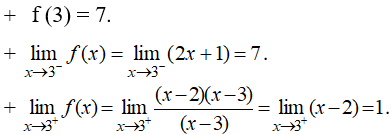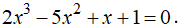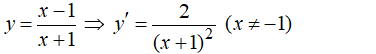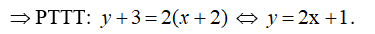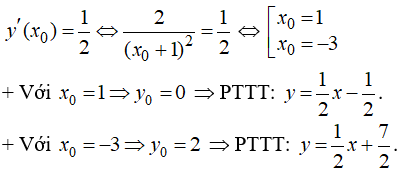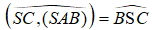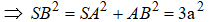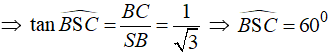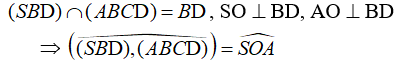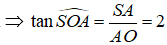Đề thi Toán 11 Học kì 2 có đáp án (Đề 2)
-
2523 lượt thi
-
35 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Phần I: Trắc nghiệm
Cho hàm số có đồ thị (C) . Khi đó tiếp tuyến của (C) tại điểm M( 1; 2003) có hệ số góc là:
Đáp án A
- Ta có: nên y’(x) = 2x + 2
- Do đó, hệ số góc của tiếp tuyến tại điểm M(1; 2003) là:
k = y’(1) = 2.1 + 2 = 4.
Câu 3:
Cho cấp số nhân lùi vô hạn có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây:
Đáp án B
- Cách giải: Cho cấp số nhân lùi vô hạn có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức
Câu 4:
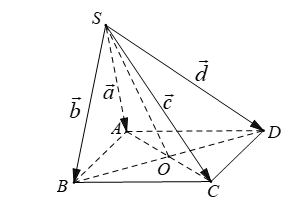
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt . Khẳng định nào sau đây đúng?
Đáp án A.
- Gọi O là tâm của hình bình hành ABCD.
Câu 5:
Hãy chọn câu đúng?
Đáp án D.
- Hai đường thẳng cùng song song với một đường thẳng thứ ba thì có thể trùng nhau ⇒ A sai.
- Hai đường thẳng không có điểm chung thì song song hoặc chéo nhau ⇒ B sai.
- Hai đường thẳng cùng song song với một mặt phẳng thì có thể cắt, trùng hoặc chéo nhau ⇒ C sai.
- Hai đường thẳng chéo nhau nếu chúng không đồng phẳng ⇒ D đúng.
Câu 6:
Trong không gian cho đường Δ và điểm O. Qua O có bao nhiêu đường thẳng vuông góc với Δ?
Đáp án B
- Phương pháp:
- Cách giải: Trong không gian cho đường thẳng Δ và điểm O. Qua O có vô số đường thẳng vuông góc Δ. Chúng nằm trong mặt phẳng qua O và vuông góc với Δ.
Câu 11:
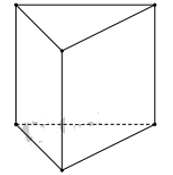
Tính chất nào sau đây không phải là tính chất của hình lăng trụ đứng:
Đáp án A
- Phương pháp: Hình lăng trụ đứng là lăng trụ có cạnh bên vuông góc với đáy.
- Cách giải: Các cạnh bên của lăng trụ đứng cùng vuông góc với đáy nên chúng song song với nhau, do đó đáp án A sai.
Câu 16:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Góc giữa SC và mp(ABCD) là góc nào?
Đáp án B
- Phương pháp: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó.
- Cách giải:
+ Ta có SA ⊥ (ABCD) ⇒ A là hình chiếu của S trên mp(ABCD)
⇒ AC là hình chiếu của SC trên mp(ABCD).
- Vậy góc giữa đường thẳng SC và mp(ABCD) là góc
Câu 17:
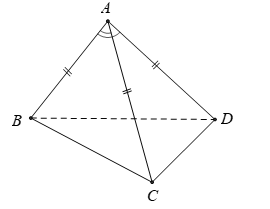
Cho tứ diện ABCD có AB = AC = AD = a và . Hãy xác định góc giữa cặp vectơ và ?
Đáp án D
- Ta có:
Câu 18:
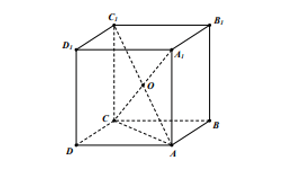
Cho hình lập phương Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng:
Đáp án B
- Phương pháp: Sử dụng công thức ba điểm và công thức hình bình hành
- Cách giải:
+ Do là hình lập phương nên là hình chữ nhật.
⇒ O là trung điểm của
+ Ta có:
Câu 20:
Hàm số y = f(x) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
Đáp án B
- Phương pháp: Hàm số y = f(x) liên tục tại điểm khi và chỉ khi
- Cách giải:
+ Dễ thấy hàm số liên tục trên (-∞ ; 1) và (1 ; +∞)
+ Dựa vào đồ thị hàm số ta thấy
→ Do đó không tồn tại
Đồng nghĩa với việc hàm số gián đoạn tại x = 1.
Câu 21:
Tìm a, b để hàm số có đạo hàm tại x = 1.
Đáp án D
- Ta có:
- Hàm có đạo hàm tại thì hàm liên tục tại x = 1 ⇔ a + b = 2 (1)
- Hàm có đạo hàm tại
Câu 22:
Cho hàm số . Tìm mệnh đề đúng trong các mệnh đề sau:
Đáp án B
- Hàm số xác định với mọi x ∈ R.
- Hàm số đã cho liên tục với mọi x ≠ 1.
- Ta có:
- Để hàm số liên tục tại x= 1 khi và chỉ khi:
- Vậy với a = 1 thì hàm số đã cho liên tục tại x = 1. Do đó, hàm số liên tục trên R.
Câu 23:
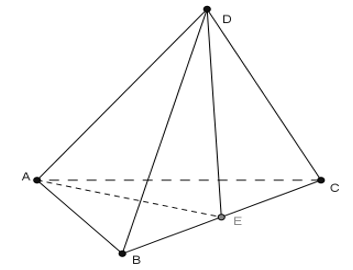
Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
Đáp án C.
- Gọi E là trung điểm của BC.
+)Tam giác ABC có AB = AC nên tam giác ABC cân tại A có AE là đường trung tuyến nên: AC ⊥ BC.
+) Tam giác BCD có DB = DC nên tam giác DBC cân tại D có DE là đường trung tuyến nên đồng thời là đường cao: DE ⊥ BC.
+) Ta có:
Câu 24:
Tìm m để tiếp tuyến của đồ thị hàm số tại điểm có hoành độ vuông góc với đường thẳng
Đáp án A
- Tập xác định: D = R.
- Đạo hàm:
- Tung độ tiếp điểm bằng 2 nên hoành độ tiếp điểm là nghiệm phương trình:
+) Tại M(1; 2) thì y’(1) = 8. Phương trình tiếp tuyến là:
y = 8(x - 1) + 2 hay y = 8x – 6.
+) Tại N(-1; 2) thì y’(-1) = -8. Phương trình tiếp tuyến là:
y = -8(x + 1) + 2 hay y = -8x - 6.
- Vậy có 2 tiếp tuyến thỏa mãn đề bài là: y = 8x – 6 và y = -8x – 6.
Câu 25:
Cho hàm số . Tập các giá trị của x để là:
Đáp án D
- Phương pháp: Sử dụng công thức
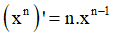
tính f'(x). Từ đó giải bất phương trình.
- Cách giải:
+ Ta có:
+ Theo đề bài ta có: 2x.f'(x) - f(x) ≥ 0.
+ Thử các đáp án:
+ Với
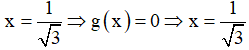
thuộc tập nghiệm của BPT.
⇒ Loại đáp án A, B và C.
Câu 30:
Xét tính liên tục của hàm số sau trên tập xác định của nó: .
Xét tính liên tục của hàm số sau trên tập xác định của nó:
● Hàm số liên tục với mọi x ≠ 3.
● Tại x = 3, ta có:
⇒ Hàm số không liên tục tại x = 3.
- Vậy hàm số liên tục trên các khoảng (-∞;3), (3;+∞).
Câu 31:
Chứng minh rằng phương trình sau có ít nhất hai nghiệm:
Chứng minh rằng phương trình sau có ít nhất hai nghiệm
- Xét hàm số: là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
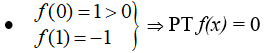
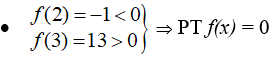
- Mà nên PT f(x) = 0 có ít nhất 2 nghiệm.
Câu 34:
Cho hàm số
a) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ .
b) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: .
a) Với x = –2 ta có: y = –3 và y'(2) = 2.
b) d: có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
- Gọi là toạ độ của tiếp điểm.
- Ta có:
Câu 35:
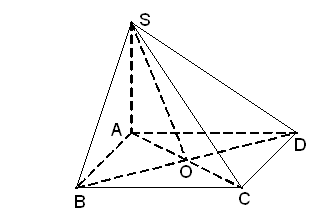
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, .
1) Chứng minh rằng các mặt bên hình chóp là những tam giác vuông.
2) Chứng minh rằng: (SAC) ⊥ (SBD).
3) Tính góc giữa SC và mp (SAB).
4) Tính góc giữa hai mặt phẳng (SBD) và (ABCD).
1)
● SA ⊥ (ABCD) ⇒ SA ⊥ AB, SA ⊥ AD.
⇒ Các tam giác SAB, SAD vuông tại A.
● BC ⊥ SA, BC ⊥ AB.
⇒ BC ⊥ SB ⇒ ΔSBC vuông tại B.
● CD ⊥ SA, CD ⊥ AD.
⇒ CD ⊥ SD ⇒ ΔSCD vuông tại D.
2)
● BD ⊥ AC, BD ⊥ SA
⇒ BD ⊥ (SAC) ⇒ (SBD) ⊥ (SAC).
3)
● BC ⊥ (SAB)
⇒
● ΔSAB vuông tại A
● ΔSBC vuông tại B
4) Gọi O là tâm của hình vuông ABCD.
● Ta có:
● ΔSAO vuông tại A