22 câu hỏi trắc nghiệm thuộc Dạng 4. Tính tuần hoàn và chu kỳ hàm lượng giác

Câu 1:

Tìm chu kì cơ sở của hàm số y=2sin2x+3cos3x .

Xem đáp án

Tập xác định $D = ℝ$ .

Chu kì hàm số $T = \frac{2 π}{|(2,3)|} = 2 π$ .

Câu 2:

Xét tính tuần hoàn và tìm chu kì của hàm số

$f (x) = \cos x + \cos (\sqrt{3} x)$ .

Xem đáp án

Giả sử hàm số đã cho tuần hoàn. Suy ra tồn tại số thực dương T thỏa mãn

$f (x + T) = f (x) \Leftrightarrow \cos (x + T) + \cos [\sqrt{3} (x + T)] = \cos x + \cos (\sqrt{3} x)$ .

Chọn $x = 0$ ta được $\cos T + \cos (\sqrt{3} T) = 2 \Leftrightarrow \{\begin{cases} \cos T = 1 \\ \cos (\sqrt{3} T) = 1 \end{cases}$

$\Rightarrow \{\begin{cases} T = 2 n π \\ \sqrt{3} T = 2 m π \end{cases} \Rightarrow \sqrt{3} = \frac{m}{n}$ (vô lí do nên là số hữu tỉ).

Vậy hàm số đã cho không tuần hoàn.

Câu 3:

Chu kì của hàm số $y = \sin (\frac{x}{3} + \frac{π}{6})$ là

A.

$\frac{1}{2}$ .

B.

$\frac{π}{3}$ .

C.

$\frac{2 π}{3}$ .

D.

$6 π$ .

Xem đáp án

Đáp án D

Hàm số $y = \sin (\frac{x}{3} + \frac{π}{6})$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{2 π}{|\frac{1}{3}|} = 6 π$ .

Câu 4:

Đồ thị trong hình vẽ dưới đây là của hàm số nào?

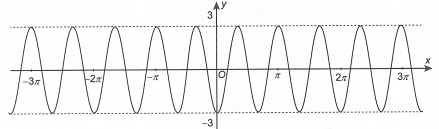
Đồ thị trong hình vẽ dưới đây là của hàm số nào? (ảnh 1)

A.

$y = \cos 3 x$ .

B.

$y = 3 \cos 3 x$ .

C.

$y = - 3 \cos 6 x$ .

D.

$y = - 3 \cos 3 x$ .

Xem đáp án

Đáp án D

Tại $x = 0 \Rightarrow y = - 3 \Rightarrow$ Loại đáp án A, B.

Tại $x = π \Rightarrow y = 3 \Rightarrow$ Loại đáp án C.

Vậy đồ thị đã cho là của hàm số .

Câu 5:

Hàm số $y = 2 \sin (\frac{x}{2} - \frac{π}{3})$ là hàm số tuần hoàn với chu kì

A.

$T = 6 π$

B.

$T = 4 π T = 4 π$ .

C. T=6.

D.

$T = 2 π$ .

Xem đáp án

Đáp án B

Hàm số $y = 2 \sin (\frac{x}{2} - \frac{π}{3})$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{2 π}{|\frac{1}{2}|} = 4 π$ .

Câu 6:

Khẳng định nào sau đây sai về hàm số y=2+sinx ?

A. Đồ thị hàm số không đi qua gốc tọa độ

B. Đồ thị hàm số nằm ở phía trên trục hoành.

C. Giá trị cực đại của y là 2.

D. Giá trị cực tiểu của y là 1.

Xem đáp án

Đáp án C

Câu 7:

Nếu chu kì tuần hoàn của hàm số $y = \sin \frac{π x}{a}$ là 4 thì

A.

$a = \pm 2$

B.

$a = \pm 4$ .

C. a=2.

D. .

$a = \pm 1$

Xem đáp án

Đáp án A

Hàm số $y = 2 \sin \frac{π x}{a}$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{2 π}{|\frac{π}{a}|} = 4 \Leftrightarrow a = \pm 2$ .

Câu 8:

Hàm số $y = \tan x^{2}$ tuần hoàn với chu kì

A.

$T = π^{2}$

B. $T = \sqrt{π}$ .

C.

$T = π$ .

D. Hàm số không có chu kì

Xem đáp án

Đáp án D

Hàm số không có chu kì cơ sở.

Câu 9:

Khẳng định nào sau đây đúng với hàm số $y = 2 \cos \frac{x}{2}$ ?

A. Biên độ là 2, chu kì là

$π$ .

B. Biên độ là -2, chu kì là

$180 °$ .

C. Biên độ là 2, chu kì là

$2 π$ .

D. Biên độ là 2, chu kì là $4 π$

Xem đáp án

Đáp án D

Chu kì của hàm số $T = \frac{2 π}{\frac{1}{2}} = 4 π .$ Loại đáp án A, B. Biên độ của hàm số $A = |2| = 2$ .

Câu 10:

Đồ thị trong hình vẽ dưới đây là của hàm số nào?

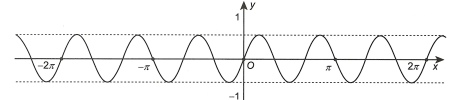
Đồ thị trong hình vẽ dưới đây là của hàm số nào? (ảnh 1)

A.

$y = \sin 2 x$ .

B.

$y = \sin 3 x$ .

C.

$y = \cos 2 x$ .

D.

$y = \cos 3 x$ .

Xem đáp án

Đáp án B

Tại $x = 0 \Rightarrow y = 0 \Rightarrow$ Loại đáp án C, D.

Chu kì của hàm số $T = \frac{2 π}{3}$ .

Vậy đồ thị đã cho là của hàm số $y = \sin 3 x$ .

Câu 11:

Chu kì của hàm số sau y=sin3x+2cos2x là

A.

$T_{0} = 2 π$ .

B.

$T_{0} = \frac{π}{2}$ .

C.

$T_{0} = π$ .

D. $T_{0} = \frac{π}{4}$ .

Xem đáp án

Đáp án A

Hàm số $f (x) = a \sin u x + b \cos v x + c$ (với $u, v \in ℤ$ ) là hàm số tuần hoàn với chu kì $T = \frac{2 π}{|(u, v)|}$

Hàm số $y = \sin 3 x + 2 \cos 2 x$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{2 π}{|1|} = 2 π$ .

Câu 12:

Với $0 \leq x \leq \frac{π}{2}$ thì hàm số $f (x) = \sin \frac{x}{3}$ có giá trị cực đại là

A. 0.

B. 1.

C.

$\frac{1}{3}$

D.

$\frac{1}{2}$ .

Xem đáp án

Đáp án D

Ta có với $0 \leq x \leq \frac{π}{2}$ thì hàm số $f (x) = \sin \frac{x}{3}$ luôn đồng biến.

Khi đó giá trị lớn nhất của hàm số là $y_{\max} = \frac{1}{2}$ tại $x = \frac{π}{2}$ .

Câu 13:

Hàm số $y = 3 \cos (\frac{π}{4} - m x)$ tuần hoàn có chu kì $T = 3 π$ khi

A.

$m = \pm \frac{3}{2}$ .

B.

$m = \pm 1$ .

C.

$m = \pm \frac{2}{3}$ .

D.

$m = \pm 2$ .

Xem đáp án

Đáp án C

Hàm số $y = 3 \cos (\frac{π}{4} - m x)$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{2 π}{|- m|} = 3 π \Leftrightarrow m = \pm \frac{2}{3}$ .

Câu 14:

Xét đồ thị hàm số $y = \sin x$ với $x \in [π,2 π]$ . Khẳng định nào sau đây đúng?

A. Đồ thị hàm số có một cực đại tại $x = π$ .

B. Đồ thị hàm số có một cực tiểu tại $x = 2 π$ .

C. Đồ thị hàm số có một cực tiểu tại $x = \frac{3 π}{2}$ .

D. Hàm số đồng biến trên $[π,2 π]$ .

Xem đáp án

Đáp án C

Hàm số $y = \sin x$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Hàm số nghịch biến trên $[π, \frac{3 π}{2}]$ . Hàm số đồng biến trên $[\frac{3 π}{2},2 π]$ .

Đồ thị hàm số có một cực tiểu tại $x = \frac{3 π}{2}$ .

Câu 15:

Đồ thị trong hình vẽ dưới đây là của hàm số nào?

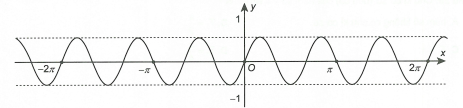
Đồ thị trong hình vẽ dưới đây là của hàm số nào? (ảnh 1)

A.

$y = \sin 2 x$ .

B.

$y = \cos 2 x$ .

C.

$y = \cos \frac{x}{2}$ .

D. $y = \cos 3 x$ .

Xem đáp án

Đáp án C

Tại $x = 0 \Rightarrow y = 1 \Rightarrow$ Loại đáp án A. Chu kì của hàm số $T = 2.2 π = 4 π$ .

Vậy đồ thị đã cho là của hàm số $y = \cos \frac{x}{2}$ .

Câu 16:

Chu kì của hàm số y=sin2x+sinx là

A.

$T = 2 π$ .

B.

$T_{0} = \frac{π}{2}$ .

C.

$T_{0} = π$ .

D.

$T_{0} = \frac{π}{4}$ .

Xem đáp án

Đáp án A

Hàm số $f (x) = a \sin u x + b \sin v x + c$ ( với $u, v \in ℤ$ ) là hàm số tuần hoàn với chu kì $T = \frac{2 π}{|(u, v)|}$ .

Hàm số $y = \sin 2 x + \sin x$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{2 π}{|1|} = 2 π$ .

Câu 17:

Chọn mệnh đề đúng trong các mệnh đề sau

A. Hàm số $y = \cot x$ đồng biến trên khoảng $(\frac{π}{2}; π)$ .

B. Hàm số $y = \sin x$ nghịch biến trên khoảng $(\frac{π}{2}; π)$ .

C. Hàm số $y = \tan x$ đồng biến trên $(- \frac{π}{2}; \frac{π}{2})$ và $y = \cot x$ nghịch biến trên khoảng $(- \frac{π}{2}; \frac{π}{2})$ .

D. Hàm số $y = \sin x$ và $y = \cos x$ cùng đồng biến trên khoảng $(0; \frac{π}{2})$ .

Xem đáp án

Đáp án B

Ta có hàm số $y = \sin x$ nghịch biến trên khoảng $(\frac{π}{2}; π)$ .

Câu 18:

Chu kì của hàm số y=tanx+tan3x là

A.

$T = 2 π$ .

B.

$T = π$ .

C.

$T = \frac{π}{4}$ .

D. $T = \frac{π}{2}$ .

Xem đáp án

Đáp án B

Hàm số $f (x) = a . \tan u x + b . \tan v x + c$ ( với $u, v \in ℤ$ ) là hàm số tuần hoàn với chu kì $T = \frac{π}{|(u, v)|}$ .

Hàm số $y = \tan x + \tan 3 x$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{π}{|1|} = π$ .

Câu 19:

Khẳng định nào sau đây đúng về hàm số $y = 2 \sin (\frac{x}{2} - 2017 π)$ ?

A. Chu kì

$2 π$ , biên độ 2.

B. Chu kì

$4 π$ , biên độ 2.

C. Chu kì

$2 π$ , biên độ 1.

D. Chu kì

$4 π$ , biên độ 1.

Xem đáp án

Đáp án B

Hàm số $y = 2 \sin (\frac{x}{2} - 2017 π)$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{2 π}{|\frac{1}{2}|} = 4 π$ .

Biên độ của hàm số $A = |2| = 2$ .

Câu 20:

Chu kì của hàm số y=sin3x+2017cos2x là

A.

$T = π$ .

B.

$T = \frac{π}{2}$ .

C.

$T = 2 π$ .

D.

$T = \frac{π}{4}$ .

Xem đáp án

Đáp án C

Hàm số $y = \sin 3 x + 2017 \cos 2 x$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Chu kì của hàm số $T = \frac{2 π}{|1|} = 2 π$ .

Câu 21:

Hình vẽ sau là đồ thị của hàm số

$y = \sin (a x + π b)$ . Biết

$a \geq 0$ và b nhỏ nhất, giá trị của biểu thức a+b là

Hình vẽ sau là đồ thị của hàm số . Biết và b nhỏ nhất, giá trị của biểu thức a+b là (ảnh 1)

A. 0

B. 1.

C. 2.

D. 3.

Xem đáp án

Đáp án B

Hàm số $y = \sin (a x + π b)$ có nghĩa $\forall x \in ℝ \Leftrightarrow D = ℝ$ .

Với $a \geq 0$ chu kì của hàm số $T = \frac{2 π}{a} = 4 π \Leftrightarrow a = \frac{1}{2}$ .

Tại $x = 0 \Rightarrow y = 1 \Rightarrow \sin (π b) = 1 \Rightarrow b = \frac{1}{2}$ .

Vậy $a + b = 1$ .

Câu 22:

Chu kì cơ sở (nếu có) của hàm số $y = \sin \sqrt{x}$ là

A. hàm số không có chu kì cơ sở.

B. $T_{0} = \frac{π}{2}$ .

C.

$T_{0} = π$ .

D. $T_{0} = \frac{π}{4}$ .

Xem đáp án

Hàm số không có chu kì cơ sở.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập chuyên đề Toán 11 Bài 1: Các công thức lượng giác cơ bản có đáp án

Dạng 4. Tính tuần hoàn và chu kỳ hàm lượng giác

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương