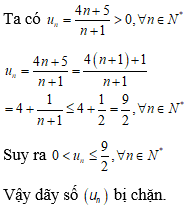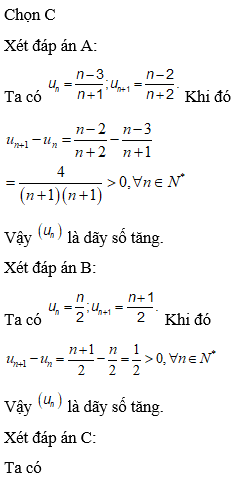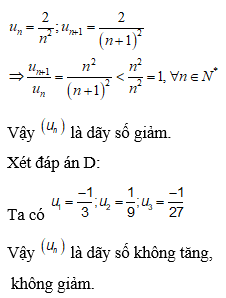Bài tập chuyên đề Toán 11 Bài 1: Phương pháp quy nạp toán học. Dãy số có đáp án
Dạng 3: Xét tính tăng, giảm và bị chặn của dãy số
-
1099 lượt thi
-
25 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 8:
Ta có
dãy là dãy số tăng.
Lại có => dãy bị chặn dưới. Dãy không bị chặn trên nên nó không bị chặn.Câu 9:
Chọn A
Ta có
Xét tỉ số
Vậy là dãy số tăng.
Câu 12:
Chọn A
Ta có
Xét hiệu
Vậy là dãy số tăng.Câu 14:
Chọn D
Dãy số là dãy số không bị chặn vì
Câu 15:
Chọn C
Nhận xét: Mỗi số hạng thứ ba trở đi luôn bằng tổng của hai số đứng ngay trước nó. Đồng thời số hạng đầu tiên và số hạng thứ hai của dãy là các số dương nên dễ thấy dãy số là một dãy tăng.Câu 16:
Chọn C
Xét hiệu
Áp dụng, ta có
Để dãy số tăng thì
Câu 17:
Chọn B
Đáp án A, C dãy không tăng, không giảm.
Xét đáp án B, ta có nên là dãy số tăng.
Câu 18:
Cho dãy số , biết . Trong các phát biểu sau, có bao nhiêu phát biểu đúng?
(1). là dãy số tăng.
(2). là dãy số bị chặn dưới.
(3).Chọn B
Vì .Phát biểu (3) đúng.
Dãy không tăng, không giảm và không bị chặn dưới.
Vậy có 1 phát biểu đúng trong 3 phát biểu đã cho.
Câu 19:
(1). là dãy số tăng.
(2). là dãy số bị chặn dưới.
(3). là dãy số bị chặn trên.
Chọn D
Ta có nên dãy số tăng. Phát biểu (1) đúng.
Vì dãy số tăng nên dãy số bị chặn dưới bởi u1. Phát biểu (2) đúng.
Ta lại có
Cộng các đẳng thức trên theo từng vế, ta được
Mặt khác
Vậy dãy số bị chặn trên bởi 2 nên phát biểu (3) đúng.
Câu 20:
Chọn C
Xét hiệu . Dãy số là dãy số tăng khi ad-bc>0
Mà c>d>0 nên chỉ có điều kiện ở đáp án C để ad-bc>0.
Câu 21:
Chọn B
Ta có
Vậy là dãy số tăng.
Câu 22:
Trong các phát biẻu sau, có bao nhiêu phát biểu đúng?
(1) Dãy số được xác định bởi là một dãy bị chặn.
(2) Dãy số được xác định bởi là một dãy giảm.
(3) Dãy số được xác định bởi là một dãy số giảm và không bị chặn dưới.
(4) Dãy số được xác định bởi là một dãy không tăng, không giảm.Chọn C
nên dãy số xác định bởi là một dãy bị chặn.
nên dãy số xác định bởi là dãy tăng.
nên dãy số xác định bởi là dãy số giảm và không bị chặn dưới.
nên dãy số xác định bởi là dãy không tăng không giảm.
Câu 23:
Chọn D
Xét hiệu
Để dãy số tăng suy ra a-1>0 => a>1Câu 24:
Chọn B
Ta có
Đặt Suy ra là cấp số nhận có công bội
Ta có
Do nên (Tn) là dãy tăng. Suy ra
Câu 25:
Chọn B
Ta có
Vậy dãy là dãy số giảm.