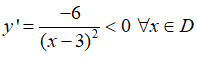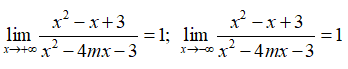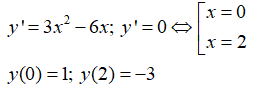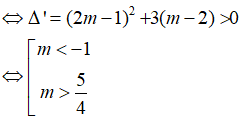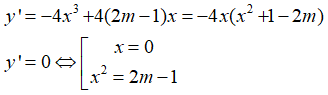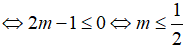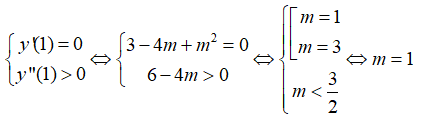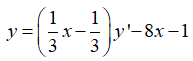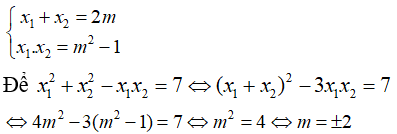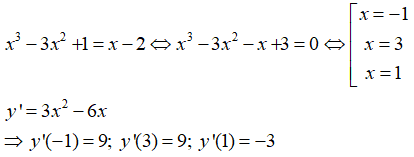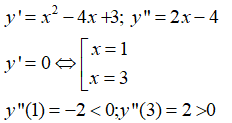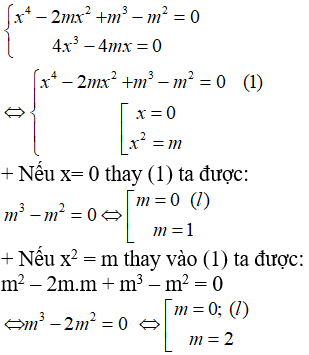Đề kiểm tra 1 tiết Giải tích 12 Chương 1 có đáp án
-
1770 lượt thi
-
20 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Kết luận nào sau đây về tính đơn điệu của hàm số là đúng?
Tập xác định: D = R\{3}
Đạo hàm
Do đó, hàm số nghịch biến trên các khoảng (-∞; 3) và (3; +∞)
Chọn C.
Câu 2:
Tìm khoảng nghịch biến của hàm số sau:
y' > 0 ⇔ x < 0; y' < 0 ⇔ x > 0
Do đó, hàm số đã cho nghịch biến trên khoảng .
Chọn B.
Câu 4:
Tìm giá trị lớn nhất của m để hàm số đồng biến trên khoảng R?
Để hàm số đã cho đồng biến trên R khi và chỉ khi:
⇔ Δ = 9 + 3m ≤ 0 ⇔ m ≤ -3
Vậy giá trị lớn nhất của m để hàm số đã cho đồng biến trên R là m = -3.
Chọn A.
Câu 5:
Đồ thị hàm số có tất cả bao nhiêu đường tiệm cận?
* Phương trình vô nghiệm
Phương trình có a.c < 0
nên phương trình luôn có 2 nghiệm phân biệt.
Suy ra, đồ thị hàm số đã cho có 2 đường TCĐ.
* Lại có:
Do đó, đồ thị hàm số đã cho có 1 TCN là y = 1.
Vậy đồ thị của hàm số đã cho có tất cả 3 đường tiệm cận.
Chọn C
Câu 6:
Cho hàm số Tích của giá trị cực đại và cực tiểu của hàm số bằng bao nhiêu?
Do đó, tích của giá trị cực đại và cực tiểu của hàm số đã cho là: 1.(-3) = - 3.
Chọn B.
Câu 7:
Tìm m để hàm số có cực đại và cực tiểu
Ta có:
Để hàm số đã cho có cực đại và cực tiểu khi và chỉ khi: phương trình có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Chọn C.
Câu 8:
Tìm m để hàm số có đúng một cực trị
Ta có:
Để hàm số đã cho có đúng 1 cực trị khi và chỉ khi phương trình: có nghiệm kép x = 0 hoặc vô nghiệm
Chọn C.
Câu 9:
Tìm m để hàm số đạt cực tiểu tại x = 1
Ta có:
Để hàm số đã cho đạt cực tiểu tại x=1 khi và chỉ khi:
Chọn B.
Câu 10:
Đồ thị hàm số có hai cực trị nằm trên đường thẳng song song với đường thẳng nào dưới đây?
Ta có:
Lấy y chia cho y’ ta được:
Giả sử đồ thị hàm số đã cho có hai điểm cực trị là: và
Suy ra, phương trình đường thẳng MN là: y = -8x – 1
Đường thẳng này song song với đường thẳng y = - 8x +1
Chọn B.
Câu 11:
Gọi là hai điểm cực trị của Tìm m để
Ta có:
Để đồ thị hàm số đã cho có 2 điểm cực trị khi và chỉ khi phương trình y’ = 0 có 2 nghiệm phân biệt và y’ đổi dấu qua các nghiệm đó.
y' = 3x^2 - 6mx + 3m^2 - 3
Do đó, hàm số đã cho có 2 điểm cực trị là nghiệm phương trình y’ = 0.
Áp dụng hệ thức Vi-et ta có:
Chọn D.
Câu 16:
Cho hàm số Ba tiếp tuyến tại giao điểm của đồ thị hàm số với đường thẳng có tổng các hệ số góc là:
Phương trình hoành độ giao điểm của hai đồ thị:
Ba tiếp tuyến tại giao điểm của đồ thị hàm số với đường thẳng y = x - 2 có tổng các hệ số góc là: 9 + 9 + (-3) = 15.
Chọn A.
Câu 17:
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
Do đó, hàm số đã cho đạt cực tiểu tại điểm x = 3 => y = -5
Phương trình tiếp tuyến tại điểm cực tiểu là:
y = 0(x - 3) – 5 = -5
Đây là đường thẳng song song với trục hoành,
Chọn B.
Câu 18:
Cho hàm số có đồ thị (C) . Phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung là:
Cho x = 0 ta được y = 1.
Do đó, giao điểm của (C) với trục tung là A(0; 1).
Phương trình tiếp tuyến tại điểm A là:
y= 3(x - 0) + 1 hay y = 3x + 1
Chọn B
Câu 19:
Tìm m để tiếp xúc với trục hoành tại hai điểm
Để đồ thị hàm số đã cho tiếp xúc với trục hoành tại hai điểm khi đồ thị hàm số đã cho có 3 điểm cực trị và đường thẳng y = 0 (trục hoành) là tiếp tuyến của đồ thị hàm số.
* Điều kiện để hàm số có 3 điểm cực trị là (*) có 3 nghiệm phân biệt
* Điều kiện để đường thẳng y = 0 ( trục hoành) là tiếp tuyến của đồ thị hàm số là hệ phương trình sau có nghiệm:
Vậy có 2 giá trị của m thỏa mãn là m = 1 hoặc m = 2
Chọn D