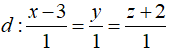200 câu trắc nghiệm Phương pháp tọa độ trong không gian nâng cao (P4)
-
7913 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Trong không gian Oxyz, cho đường thẳng và mặt phẳng (α): x + y -z – 2 = 0. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng (α), đồng thời vuông góc và cắt đường thẳng d?
Chọn C
Phương trình tham số của đường thẳng
Lấy I ∈ d => I (1 + t; 2 + 2t; 3+ t), I ∈ (α) => 1 + t + 2 + 2t – (3 + t) - 2 = 0 ó t = 1 => I (2; 4; 4)
Vectơ chỉ phương của d là
Vectơ chỉ pháp tuyến của (α) là
Ta có
Đường thẳng cần tìm qua điểm I (2; 4; 4), nhận một VTCP có tọa độ là (-3; 2; -1) nên có
Kiểm tra A (5; 2; 5) ∈ Δ3 (với t = -1) , thấy A (5; 2; 5) thỏa mãn phương trình (*)
Câu 2:
Trong không gian Oxyz, cho mặt phẳng (α): 2x + y -2z – 2 = 0, đường thẳng và điểm . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng Δ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng.
Chọn A
Cách 1: Ta có: B ∈ Oxy và B ∈ (α) nên B (a ; 2 – 2a ; 0).
đi qua M (-1 ; -2 ; -3) và có một véctơ chỉ phương là
Ta có: d ⊂ (α) nên d và Δ song song với nhau và cùng nằm trong mặt phẳng (α).
Gọi C = d ∩ (Oxy) nên
Gọi d’ = (α) ∩ (Oxy), suy ra d’ thỏa hệ
Do đó, d’ qua và có VTCP
Gọi H là hình chiếu của C lên Δ. Ta có CH = 3 và
Cách 2: Ta có: đi qua M (-1 ; -2 ; -3) và có một VTCP là
Ta có: B = Δ ∩ (Oxy), Δ ⊂ (α) nên B ∈ (Oxy) ∩ (α) => B (a; 2 – a; 0)
Ta có: Δ // d và d (Δ, d) = 3 nên
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung điểm của SC, SD (tham khảo hình vẽ bên).
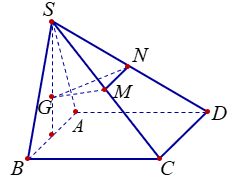
Tính côsin của góc giữa hai mặt phẳng (GMN) và (ABCD)
Chọn C
Cách 1: Chọn hệ trục tọa độ Oxyz như hình vẽ.
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là , mặt phẳng (GMN) có vectơ pháp tuyến là
Gọi α là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có
Cách 2:
Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD. Hình chiếu của ΔGMN lên (ABCD) là ΔHEF =>
Cách 3:
Gọi H, I lần lượt là trung điểm của AB, CD. J = SI ∩ MN, K = GJ ∩ HI
Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là
Câu 4:
Trong không gian Oxyz, cho mặt phẳng x – z – 3 = 0 và điểm M (1; 1; 1). Gọi A là điểm thuộc tia Oz. Gọi B là hình chiếu của A lên (α). Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB bằng:
Chọn B
Gọi A (0; 0; a). Đường thẳng AB qua A và vuông góc với (α) có phương trình
B là hình chiếu của A lên (α) nên tọa độ B thỏa mãn hệ
Tam giác MAB cân tại M nên
· Nếu a = -3 thì tọa độ A (0; 0; -3) và B (0; 0; -3) trùng nhau, loại.
· Nếu a = 3 thì tọa độ A (0; 0; 3), B (3; 0; 0)
Diện tích tam giác MAB bằng
Câu 5:
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục Oz sao cho MA2 + MB2 đạt giá trị nhỏ nhất.
Chọn C
Gọi I là trung điểm của AB
Suy ra: MA2 + MB2 đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=>M là hình chiếu của I trên trục Oz => M (0 ; 0 ; 3)
Câu 6:
Trong không gian tọa độ Oxyz, cho điểm M (2; 0; 0), N (1; 1; 1). Mặt phẳng (P) thay đổi qua M, N cắt các trục Ox, Oy lần lượt tại B (0; b; 0), C (0; 0; c) (b, c > 0). Hệ thức nào dưới đây là đúng?
Chọn A
Câu 8:
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1; 0; -1), B (2; 3; -1), C (-2; 1; 1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
Chọn A
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0; 2; 0)
Đường thẳng d cần tìm đi qua I (0; 2; 0) và nhận vectơ làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là
Câu 9:
Trong không gian tọa độ Oxyz, cho các điểm A (1; 2; 3), B (2; 1; 0), C (4; 3; -2), D (3; 4; 1), E (1; 1; -1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
Chọn C
Suy ra ABCD là hình bình hành.
=>E.ABCD là hình chóp đáy là hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên.
+ Mặt phẳng qua 4 trung điểm lần lượt của ED, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt của EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, EB, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, ED, AB, DC.
Câu 10:
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng . Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
Câu 11:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và điểm A (1; 2; 3). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.
Chọn B
Nhận xét: Cho ba mặt phẳng đôi một vuông góc với nhau (P), (Q), (R) tại I. Hạ AH, AD, AE lần lượt vuông góc với ba mặt phẳng trên thì ta luôn có: IA2 = AD2 + AH2 + AE2
Chứng minh: Chọn hệ trục tọa độ với I(0; 0; 0), ba trục Ox, Oy, Oz lần lượt là ba giao tuyến của ba mặt phẳng (P), (Q), (R). Khi đó A (a; b; c) thì IA2 = a2 + b2 + c2 = d2 (A, (Iyz)) + d2(A, (Ixz)) + d2(A, (Ixy)) hay IA2 = AD2 + AH2 + AE2 (đpcm)
Áp dụng: Mặt cầu (S) có tâm I (1; -1; 2) và có bán kính r = 4;
Gọi Ii và rj là tâm và bán kính của các đường tròn I (1; 2; 3)
Ta có tổng diện tích các đường tròn là:
Câu 12:
Trong không gian với hệ tọa độ Oxyz cho điểm A (2; 1; 3) và mặt phẳng (P): x + my + (2m + 1)z – m – 2 = 0, m là tham số. Gọi H (a; b; c) là hình chiếu vuông góc của điểm A trên (P). Tính a + b khi khoảng cách từ điểm A đến (P) lớn nhất?
Chọn D
Ta có x + my + (2m + 1)z – m – 2 = 0 <=> m(y + 2z -1) + x + z - 2 = 0 (*)
Phương trình (*) có nghiệm với
Suy ra (P) luôn đi qua đường thẳng
Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = a,SA = a và SA vuông góc với đáy ABCD. Tính sinα, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC)
Chọn C
Đặt hệ trục tọa độ Oxyz như hình vẽ. Khi đó, ta có A (0; 0; 0), B (a; 0; 0), C(a; ; 0); D (0; a√3; 0), S (0; 0; a)
Ta có , nên đường thẳng BD có vectơ chỉ phương là
Như vậy, mặt phẳng (SBC) có vectơ pháp tuyến là . Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì:
Câu 14:
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; 2; 3) và mặt phẳng (P): 2x + y - 4z + 1 = 0, đường thẳng d đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.
Chọn B
Gọi B(0; 0; b) là giao điểm của đường thẳng d và trục Oz.
Vì đường thẳng d song song với mặt phẳng (P) nên:
Do đó đường thẳng d đi qua điểm B(0; 0; 2) và nhận VTCP có tọa độ là (1; 2; 1)
Suy ra phương trình tham số của đường thẳng d là:
Câu 18:
Trong không gian tọa độ Oxyz, cho điểm A(1;-2; 3). Gọi (S) là mặt cầu chứa A có tâm I thuộc tia Ox và bán kính bằng 7. Phương trình mặt cầu (S) là:
Chọn D
Vì tâm I thuộc tia Ox nên I (m; 0; 0) với m > 0
Vì (S) chứa A và có bán kính bằng 7 nên: IA = 7
Khi m = 7 thì I(7; 0; 0)
Phương trình mặt cầu cần tìm là:
Câu 19:
Trong không gian Oxyz, cho bốn đường thẳng:
Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
Chọn D
Đường thẳng d1 đi qua điểm M1 (3; -1; -1) và có một véctơ chỉ phương là
Đường thẳng d2 đi qua điểm M2 (0; 0; 1) và có một véctơ chỉ phương là
Do và M1 ∉ d1 nên hai đường thẳng d1 và d2 song song với nhau.
Gọi (α) là mặt phẳng chứa d1 và d2 khi đó (α) có một véctơ pháp tuyến là
Phương trình mặt phẳng (α) là x + y + z -1 = 0
Gọi A = d3 ∩ (α) thì A (1; -1; 1)
Gọi B = d4 ∩ (α) thì B (-1; 2; 0)
Do không cùng phương với
Nên đường thẳng AB cắt hai đường thẳng d1 và d2.
Vậy có 1 đường thẳng thỏa mãn yêu cầu bài toán.
Câu 20:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-y+z-10 = 0 và đường thẳng ![]() . Đường thẳng Δ cắt (P) và d lần lượt tại M và N sao cho A(1;3;2) là trung điểm MN. Tính độ dài đoạn MN.
. Đường thẳng Δ cắt (P) và d lần lượt tại M và N sao cho A(1;3;2) là trung điểm MN. Tính độ dài đoạn MN.
Chọn C
Vì N = Δ ∩ d nên N ∈ d, do đó N(-2+2t; 1+t; 1-t). Mà A (1;3;2) là trung điểm MN nên
Vì M = Δ ∩ (P) nên M ∈ (P), do đó 2(4-2t)-(5-t)+(3+t)-10=0 ⇔ t= -2.
Suy ra M (8;7;1) và N (-6;-1;3).
Câu 21:
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4), B(1;-3;1), C(2;2;3). Tính đường kính d của mặt cầu (S) đi qua ba điểm trên và có tâm nằm trên mặt phẳng (Oxy).
Chọn C
Gọi tâm mặt cầu là: I(x;y;0).
Câu 22:
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
Chọn A
Gọi A(a; 0; 0);B(0; b; 0);C(0; 0; c)
Phương trình mặt phẳng (P) có dạng:
Vì M là trực tâm của tam giác ABC nên:
Khi đó phương trình (P): 3x + 2y + z - 14 = 0.
Vậy mặt phẳng song song với (P) là: 3x + 2y + z + 14 = 0.
Câu 23:
Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SA và BC. Biết góc giữa MN và mặt phẳng (ABC) bằng 60°. Khoảng cách giữa hai đường thẳng BC và DM là:
Gọi O là giao của AC và BD. Khi đó
Gọi I là trung điểm OA. Vì IM// SO ⇒ IM⊥(ABCD) nên hình chiếu của MN lên (ABCD) là IN. Suy ra
Áp dụng định lí cô sin trong ΔCIN, ta có:
Ta có d(BC, DM) = d(BC, (SAD)) = d(N, (SAD)) = 2d(O, (SAD)) = 2d(O, (SBC)).
Kẻ OE ⊥ SN ⇒ OE ⊥ (SBC).
Ta có d(O, (SBC)) = OE mà
Câu 24:
Trong không gian với hệ tọa độ Oxyz, cho ΔABC biết A(2;0;0), B(0;2;0), C(1;1;3). Gọi H(x0;y0;z0) là chân đường cao hạ từ đỉnh A xuống BC. Khi đó x0 + y0 + z0 bằng:
Chọn B
Câu 25:
Cho tứ diện ABCD có các cạnh AB, AC, AD vuông góc với nhau từng đôi một và AB = 3a , AC = 6a, AD = 4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, DB. Tính thể tích khối đa diện AMNP.
Chọn A
Cách 1: Khối tứ diện ABCD được chia thành bốn tứ diện có thể tích bằng nhau.
Cách 2:
Mà M, N, P là trung điểm các cạnh BC, CD, BD nên hai tam giác BCD và MNP đồng dạng theo tỉ số