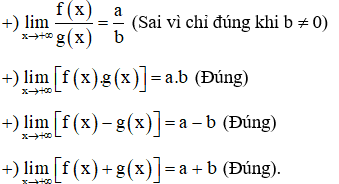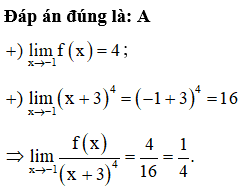38 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 9)

Câu 1:

\lim_{x \to 1} (3 x^{2} - 2 x + 1)

bằng:

A. 1;

B. 2;

C. 3;

D. +¥.

Xem đáp án

Đáp án đúng là: B

Ta có $\lim_{x \to 1} (3 x^{2} - 2 x + 1) = {3.1}^{2} - 2.1 + 1 = 2.$

Câu 2:

Cho hàm số $f (x) = \{\begin{matrix} \frac{x^{2} - 1}{x - 1} k h i x \neq 1 \\ m k h i x = 1 \end{matrix}$ với m là tham số thực. Tìm m để hàm số liên tục tại x = 1.

A. m = 2;

B. m = -1;

C. m = -2;

D. m = 1.

Xem đáp án

Cho hàm số f= x^2-1/x-1 m với m là tham số thực (ảnh 1)

Câu 3:

Cho các hàm số f, g có giới hạn hữu hạn khi x dần tới x₀. Khẳng định nào sau đây đúng?

A. $\lim_{x \to x_{0}} |f (x) + g (x)| = \lim_{x \to x_{0}} [f (x) + g (x)];$

B. $\lim_{x \to x_{0}} |f (x) + g (x)| = |\lim_{x \to x_{0}} [f (x) + g (x)]|;$

C. $\lim_{x \to x_{0}} |f (x) + g (x)| = \lim_{x \to x_{0}} |f (x)| + \lim_{x \to x_{0}} |g (x)|;$

D. $\lim_{x \to x_{0}} |f (x) + g (x)| = \lim_{x \to x_{0}} f (x) + \lim_{x \to x_{0}} g (x) .$

Xem đáp án

Đáp án đúng là: B

Các hàm số f, g có giới hạn hữu hạn khi x dần tới x₀thì: $\lim_{x \to x_{0}} |f (x) + g (x)| = |\lim_{x \to x_{0}} [f (x) + g (x)]| .$

Câu 4:

Giá trị của giới hạn $\lim_{x \to 3} \frac{x^{2} - 9}{x - 3}$ bằng:

A. -3;

B. 3;

C. 6;

D. +¥.

Xem đáp án

trị của giới hạn lĩm đến 3 x^2-9/x-3 bằng (ảnh 1)

Câu 5:

Giới hạn $\lim_{x \to 0} \frac{\sqrt[3]{1 + 4 x} - 1}{x}$ có giá trị bằng:

A. +¥;

B. $\frac{4}{3};$

C. -¥;

D. 0.

Xem đáp án

Giới hạn lim x đến 0 cưn ba 1+4x-1/x có giá trị bằng: (ảnh 1)

Câu 6:

Tính giới hạn

\lim \frac{n^{2} - 3 n^{3}}{2 n^{3} + 5 n - 2}

A. $\frac{1}{5};$

B. $\frac{1}{2};$

C. $- \frac{3}{2};$

C. 0

Xem đáp án

Câu 7:

Giá trị của giới hạn $\lim \frac{1 - 2 n}{3 n + 1}$ bằng:

A. - 5

B. $- \frac{2}{3};$

C. $\frac{1}{3}$

D. 7

Xem đáp án

Giá trị của giới hạn 1-2n/3n+1 bằng: (ảnh 1)

Câu 8:

Giả sử ta có $\lim_{x \to + \infty} f (x) = a$ và $\lim_{x \to + \infty} g (x) = b, (a, b \in ℝ) .$ Trong các mệnh đề sau, mệnh đề nào sai?

A. $\lim_{x \to + \infty} \frac{f (x)}{g (x)} = \frac{a}{b};$

B. $\lim_{x \to + \infty} [f (x) . g (x)] = a . b;$

C. $\lim_{x \to + \infty} [f (x) - g (x)] = a - b;$

D. $\lim_{x \to + \infty} [f (x) + g (x)] = a + b .$

Xem đáp án

Giả sử ta có và Trong các mệnh đề sau, mệnh đề nào sai? (ảnh 1)

Câu 9:

Trong không gian, cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt $\vec{S A} = \vec{a}; \vec{S B} = \vec{b}; \vec{S C} = \vec{c}; \vec{S D} = \vec{d} .$ Khẳng định nào sau đây đúng?

A. $\vec{a} + \vec{d} = \vec{b} + \vec{c};$

B. $\vec{a} + \vec{c} + \vec{d} + \vec{b} = \vec{0};$

C. $\vec{a} + \vec{b} = \vec{c} + \vec{d};$

D. $\vec{a} + \vec{c} = \vec{d} + \vec{b} .$

Xem đáp án

Trong không gian, cho hình chóp S.ABCD có đáy ABCD (ảnh 1)

Câu 10:

Trong không gian, cho hình lập phương ABCD.A₁B₁C₁D₁ có cạnh a. Gọi M là trung điểm AD. Giá trị $\vec{B_{1} M} . \vec{B D_{1}}$ là:

A. a²;

B. $\frac{3}{2} a^{2};$

C. $\frac{3}{4} a^{2};$

D. $\frac{1}{2} a^{2} .$

Xem đáp án

Trong không gian, cho hình lập phương ABCD.A1B1C1D1 (ảnh 1)

Câu 11:

Giá trị của $\lim \frac{2020^{n} - 2022^{n + 1}}{{2021.2022}^{n}}$ bằng

A. - 1

B. $\frac{2022}{2021};$

C. 0

D. $- \frac{2022}{2021};$

Xem đáp án

Giá trị của lim 2020^n-2021^n+1/2021.2022^n bằng (ảnh 1)

Câu 12:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song hoặc trùng với đường thẳng c;

B. Góc giữa hai đường thẳng là góc nhọn

C. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c;

D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó.

Xem đáp án

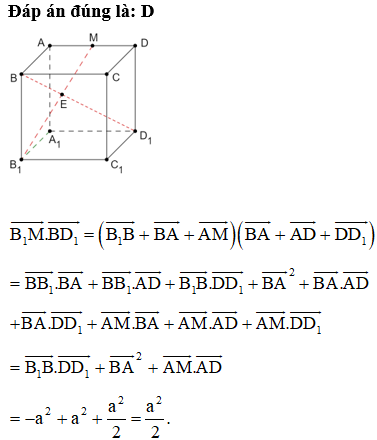
Đáp án đúng là: A

+) Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song hoặc trùng với đường thẳng c (Đúng).

+) Góc giữa hai đường thẳng là góc nhọn (Sai vì có thể là góc vuông).

+) Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c (Sai vì b có thể trùng với c).

+) Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó (Sai vì góc của hai véc-tơ có thể là góc tù).

Câu 13:

Biết

\lim_{x \to - 1} f (x) = 4.

Khi đó

\lim_{x \to - 1} \frac{f (x)}{{(x + 3)}^{4}}

có giá trị bằng:

A. $\frac{1}{4};$

B. 4

C. +¥;

D. 0

Xem đáp án

Biết lim x đến -1 fx=4 Khi đó lim x đến -1 fx/x+3^4 có giá trị bằng: (ảnh 1)

Câu 14:

Trong không gian, cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?

A. CD ^ (ABD);

B. AC ^ BD;

C. AB ^ (ABC);

D. BC ^ AD.

Xem đáp án

Trong không gian, cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng? (ảnh 1)

Câu 15:

Giới hạn $\lim_{x \to + \infty} \frac{c x^{2} + a}{x^{2} + b}$ có giá trị bằng:

A. a

B. $\frac{a + b}{c};$

C. b

D. c

Xem đáp án

Đáp án đúng là: D

Ta có $\lim_{x \to + \infty} \frac{c x^{2} + a}{x^{2} + b} = \lim_{x \to + \infty} \frac{c + \frac{a}{x^{2}}}{1 + \frac{b}{x^{2}}} = c .$

Câu 16:

Cho dãy số (u_n) thỏa mãn lim (u_n - 5) = 3. Giá trị của lim u_n bằng

A. 3;

B. 8;

C. 5;

D. 2.

Xem đáp án

Cho dãy số (un) thỏa mãn lim (un  5) = 3. Giá trị của lim un bằng (ảnh 1)

Câu 17:

Trong không gian, cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây đúng?

A. Nếu a và b cùng nằm trong mp (a) và mp (a) // c thì góc giữa a và c bằng góc giữa b và c;

B. Nếu góc giữa a và c bằng góc giữa b và c thì a // b;

C. Nếu a // b và c ^ a thì c ^ b;

D. Nếu a và b cùng vuông góc với c thì a // b.

Xem đáp án

Đáp án đúng là: C

+) Nếu a và b cùng nằm trong mp (a) và mp (a) // c thì góc giữa a và c bằng góc giữa b và c (Sai).

+) Nếu góc giữa a và c bằng góc giữa b và c thì a // b (Sai).

+) Nếu a // b và c ^ a thì c ^ b (Đúng).

+) Nếu a và b cùng vuông góc với c thì a // b (Sai vì a, b có thể cắt nhau).

Câu 18:

Trong không gian, cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ

\vec{A B}

và

\vec{D H}

?

A. 120°;

B. 60°;

C. 45°;

D. 90°.

Xem đáp án

Trong không gian, cho hình lập phương ABCD.EFGH. Hãy xác đị (ảnh 1)

Câu 19:

Hàm số nào trong các hàm số sau không liên tục trên khoảng (0; 3):

A. y = cot x;

B. y = sin x;

C. y = tan x;

D. y = cos x.

Xem đáp án

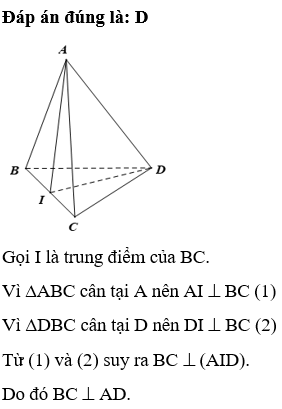
Đáp án đúng là: C

Ta có y = sin x và y = cos x là hai hàm liên tục trên ℝ.

Câu 20:

Phát biểu nào sau đây là sai?

A. $\lim \frac{1}{n} = 0;$

B. lim u_n = c (u_n = c là hằng số);

C. $\lim \frac{1}{n^{k}} = 0 (k > 1);$

D. lim qⁿ = 0 (|q| > 1).

Xem đáp án

Đáp án đúng là: D

lim qⁿ = 0 (|q| > 1) (Sai vì |q| < 1).

Câu 21:

Giá trị của tham số a để hàm số liên tục tại điểm x = 1 là

A. $\frac{1}{2};$

B. -1

C. $- \frac{1}{2};$

D. 1

Xem đáp án

Giá trị của tham số a để hàm số fx căn x-1/x-1 liên tục (ảnh 1)

Câu 22:

Cho tứ diện ABCD. Gọi P, Q là trung điểm của AB và CD. Chọn khẳng định đúng?

A. $\vec{P Q} = \vec{B C} + \vec{A D};$

B. $\vec{P Q} = \frac{1}{2} (\vec{B C} + \vec{A D});$

C. $\vec{P Q} = \frac{1}{2} (\vec{B C} - \vec{A D});$

D. $\vec{P Q} = \frac{1}{4} (\vec{B C} + \vec{A D}) .$

Xem đáp án

Cho tứ diện ABCD. Gọi P, Q là trung điểm của AB và CD. Chọn khẳng định đúng? (ảnh 1)

Câu 23:

Dãy số nào sau đây có giới hạn bằng 0

A.( 1,101)ⁿ;

B. ${(\sqrt{2})}^{n};$

C. (-1,101)ⁿ;

D. (0,919)ⁿ.

Xem đáp án

Đáp án đúng là: D

Với |q| < 1 thì lim qⁿ = 0

Vậy lim (0,919)ⁿ = 0.

Câu 24:

Giới hạn $\lim_{x \to 3^{+}} \frac{x - 3}{\sqrt{x^{2} - 9}}$ có giá trị bằng:

A. 0

B. -¥;

C. +¥;

D. $\sqrt{6} .$

Xem đáp án

Giới hạn lim x đến 3+ x-3/ cưn x^2-9 có giá trị bằng: (ảnh 1)

Câu 25:

Giới hạn $\lim_{x \to 1} \frac{\sqrt{x + 3} - 2}{x - 1}$ có giá trị bằng:

A. $\frac{1}{4};$

B. -1

B. $\frac{2}{3};$

D. $\frac{5}{4} .$

Xem đáp án

Giới hạn lim x đến 1 căn x+3-2/x-1 có giá trị bằng: (ảnh 1)

Câu 26:

Cho hàm số f (x) xác định trên đoạn [a, b]. Trong các mệnh đế sau, mệnh đề nào đúng?

A. Nếu phương trình f (x) = 0 có nghiệm trong khoảng (a, b) thì hàm số f (x) phải liên tục trên khoảng (a, b);

B. Nếu hàm số f (x) liên tục trên đoạn [a, b] và f (a).f (b) > 0 thì phương trình f (x) = 0 không có nghiệm trong khoảng (a, b);

C. Nếu hàm số f (x) liên tục, tăng trên đoạn [a, b] và f (a).f (b) > 0 thì phương trình f (x) = 0 không thể có nghiệm trong khoảng (a, b);

D. Nếu f (a).f (b) < 0 thì phương trình f (x) = 0 có ít nhất một nghiệm trong khoảng (a, b).

Xem đáp án

Đáp án đúng là: C

Nếu hàm số f (x) liên tục, tăng trên đoạn [a, b] và f (a).f (b) > 0 thì phương trình f (x) = 0 không thể có nghiệm trong khoảng (a, b)

Câu 27:

Trong bốn giới hạn sau, giới hạn nào bằng 0?

A. $\lim \frac{2^{n} + 3}{1 - 2^{n}};$

B. $\lim \frac{2^{n} + 1}{{3.2}^{n} - 3^{n}};$

C. $\lim \frac{1 - n^{3}}{n^{2} + 2 n};$

D. $\lim \frac{(2 n + 1) {(n - 3)}^{2}}{n - 2 n^{3}} .$

Xem đáp án

Trong bốn giới hạn sau, giới hạn nào bằng 0? (ảnh 1)

Câu 28:

Cho hàm số $f (x) = \frac{1}{x - 2} .$ Tìm khẳng định đúng trong các khẳng định sau

A. Hàm số liên tục trên (1; 3);

B. Hàm số liên tục trên ℝ;

C. Hàm số gián đoạn tại x = 2;

D. Hàm số gián đoạn tại x = 1.

Xem đáp án

Cho hàm số fx=1/x-2 Tìm khẳng định đúng trong các khẳng định sau (ảnh 1)

Câu 29:

Giới hạn $\lim [\frac{1}{1.2} + \frac{1}{2.3} + \cdot \cdot \cdot + \frac{1}{n (n + 1)}]$ có giá trị bằng:

A. $\frac{3}{2};$

B. 2

C. 0

D. 1

Xem đáp án

Giới hạn lim 1/1.2+1/2.3+...1/n.(n+1) có giá trị bằng: (ảnh 1)

Câu 30:

Trong không gian, cho hình chóp S.ABC có SA ^ ( ABC) và ∆ABC vuông ở B. AH là đường cao của ∆SAB. Khẳng định nào sau đây sai

A. AH ^ SC

B. SA ^ BC;

C. AH ^ BC;

D. AH ^ AC

Xem đáp án

Trong không gian, cho hình chóp S.ABC có SA  ( (ảnh 1)

Câu 31:

Ta có $\lim_{x \to - \infty} \frac{x - \sqrt{x^{2} + x}}{x + 1} = \frac{a}{b}$ với a, b Î ℕ và $\frac{a}{b}$ tối giản. Khi đó, giá trị của 2a - b là:

A. 4

B. 2

C. 3

D. 1

Xem đáp án

Ta có lim x đến âm vô cùng x-căn x^2+x/x+1 với a, b thuộc ℕ và tối giản. Khi đó (ảnh 1)

Câu 32:

Trong không gian, cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ^ (ABCD). Mặt phẳng qua A và vuông góc với SC cắt SB, SC, SD theo thứ tự tại H, M, K. Chọn khẳng định sai trong các khẳng định sau?

A. HK ^ AM;

B. AK ^ HK;

C. BD // HK;

D. AH ^ SB.

Xem đáp án

Trong không gian, cho hình chóp S.ABCD có đáy ABCD là hình (ảnh 1)

Câu 33:

Cho $\lim \frac{a n + \sqrt{n^{2} + n + 1}}{2 n - 1} = 2.$ Khẳng định nào sau đây là đúng?

A. a Î [1; 2);

B. a Î (-¥; 1);

C. a Î [2; +¥);

D. a Î [-1; 1).

Xem đáp án

Cho an+ căn n^2+n+1/2n-1 Khẳng định nào sau đây là đúng? (ảnh 1)

Câu 34:

Cho góc giữa $|\vec{a}| = 3; |\vec{b}| = 5;$ và bằng 120°. Chọn khẳng định sai trong các khẳng định sau?

A. $|\vec{a} + 2 \vec{b}| = 9;$

B. $|\vec{a} - 2 \vec{b}| = \sqrt{139};$

C. $|\vec{a} + \vec{b}| = \sqrt{19};$

D. $|\vec{a} - \vec{b}| = 7.$

Xem đáp án

Cho góc giữa và bằng 120. Chọn khẳng định sai trong các khẳng định sau? (ảnh 1)

Câu 35:

Cho hàm số y = f (x) xác định tại mọi điểm x ¹ 0 thỏa mãn

f (x) + 2 f (\frac{1}{x}) = 3 x, ​ x \neq 0.

Khi đó, giá trị của giới hạn

\lim_{x \to \sqrt{2}} \frac{f (x)}{x - \sqrt{2}}

bằng

A. $2 \sqrt{2};$

B. 2

C. $- 2 \sqrt{2};$

D. -2

Xem đáp án

Cho hàm số y = f (x) xác định tại mọi điểm x (ảnh 1)

Câu 36:

Tính giới hạn của dãy số $\lim (\sqrt{n^{2} + 2 n + 5} - n + 3)$

Xem đáp án

Tính giới hạn của dãy số lim căn n^2+2n+5-n+3 (ảnh 1)

Câu 37:

Cho hai hình chữ nhật ABCD, ABEF nằm trên hai mặt phẳng khác nhau sao cho hai đường chéo AC và BF vuông góc. Gọi CH là đường cao của tam giác BCE. Chứng minh rằng BF ^ AH

Xem đáp án

Cho hai hình chữ nhật ABCD, ABEF nằm trên hai mặt phẳng khác nhau sao cho hai đường chéo AC và BF vuông góc. (ảnh 1)

Câu 38:

Chứng minh rằng phương trình m(x - 1)³(x² - 4) + x⁴ - 3 = 0 luôn có ít nhất hai nghiệm phân biệt với mọi giá trị m

Xem đáp án

Ta có:

+) f (x) = m(x - 1)³(x² - 4) + x⁴ - 3 = 0 liên tục trên ℝ nên f (x) liên tục trên đoạn [-2; 1] (1)

Mặt khác:

+) f(–2) = m(–2 – 1)³ . [(–2)² – 4] + (–2)⁴ – 3 = 13;

+) f(1) = m(1 – 1)³ . (1² – 4) + 1⁴ – 3 = –2.

Do đó f (-2).f (1) = 13.(-2) = - 26 < 0 (2)

Từ (1) và (2) nên f (x) = 0 cho ít nhất 1 nghiệm x thuộc [-2; 1] (*)

+) f (x) = m(x - 1)³(x² - 4) + x⁴ - 3 = 0 liên tục trên ℝ nên f (x) liên tục trên đoạn [1; 2] (3)

Ta lại có:

+) f(2) = m.(2 – 1)³ . (2² – 4) + 2⁴ – 3 = 13;

+) f(1) = m(1 – 1)³ . (1² – 4) + 1⁴ – 3 = –2.

Do đó f (2).f (1) = 13.(-2) = - 26 < 0 (4)

Từ (3) và (4) nên f (x) = 0 cho ít nhất 1 nghiệm x thuộc [1; 2] (**)

Từ (*) và (**) nên suy ra f (x) = 0 cho ít nhất hai nghiệm phân biệt thuộc [-2; 2]

Vậy phương trình m(x - 1)³(x² - 4) + x⁴ - 3 = 0 luôn có ít nhất hai nghiệm phân biệt với mọi giá trị m.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 9)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương