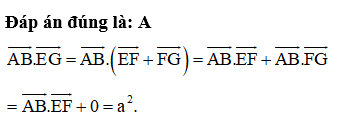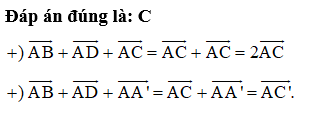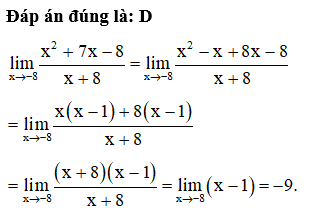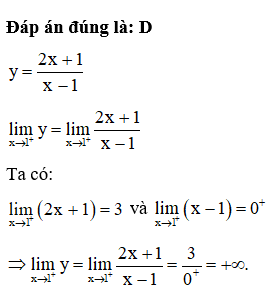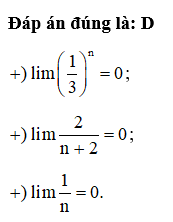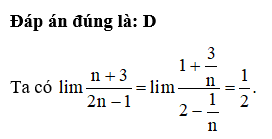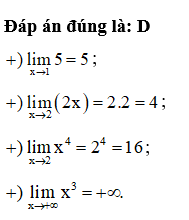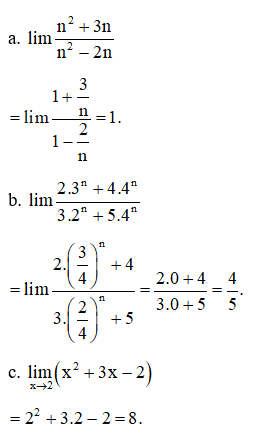24 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 14)

Câu 1:

f (x) = \{\begin{matrix} 2 x + 1 k h i x \neq 2 \\ a k h i x = 2 \end{matrix}

tìm a để hàm số liên tục tại x = 2.

A. a = -5;

B. a = 1;

C. a = 4;

D. a = 5

Xem đáp án

Cho hàm số fx = 2x+1 a tìm a để hàm số liên tục (ảnh 1)

Câu 2:

Chọn đẳng thức đúng

A. $\vec{A B} - \vec{A C} = \vec{B C};$

B. $\vec{A B} + \vec{C A} = \vec{B C};$

C. $\vec{C B} + \vec{C A} = \vec{A B};$

D. $\vec{A B} + \vec{B C} = \vec{A C} .$

Xem đáp án

Đáp án đúng là: D

$+) \vec{A B} - \vec{A C} = \vec{C B} +) \vec{A B} + \vec{C A} = \vec{C A} +) \vec{C B} + \vec{C A} = 2 \vec{C O} (V ớ i O l à t r u n g đ i ể m c ủ a A B)$

$+) \vec{A B} + \vec{B C} = \vec{A C} .$

Câu 3:

Cho hình hộp ABCD.EFGH ba vectơ nào sau đây đồng phẳng

A. $\vec{C B}, \vec{A C}, \vec{B E};$

B. $\vec{E F}, \vec{F H}, \vec{E G};$

C. $\vec{A B}, \vec{B C}, \vec{A E};$

D. $\vec{D B}, \vec{A C}, \vec{D F} .$

Xem đáp án

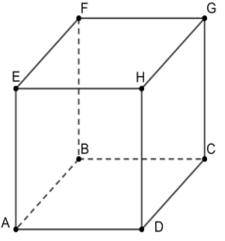
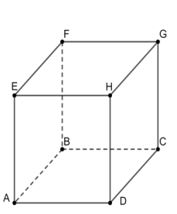
$+) \vec{E F}, \vec{F H}, \vec{E G}$ là ba véc-tơ có giá cùng song song với mặt phẳng (ABCD) nên chúng cùng thuộc một mặt phẳng và đó là mặt phẳng (EFGH).

Câu 4:

Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính tích vô hướng

\vec{A B} . \vec{E G}

bằng:

A. a²;

B. $\frac{a^{2} \sqrt{2}}{2};$

C. $a^{2} \sqrt{3};$

D. $a^{2} \sqrt{2} .$

Xem đáp án

Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính tích vô hướng bằng: (ảnh 2)

Câu 5:

Cho hình hộp ABCD.A’B’C’D’ chọn khẳng định đúng

A. $\vec{A B} + \vec{A D} + \vec{A C} = \vec{A C'};$

B. $\vec{A B} + \vec{A D} + \vec{A A'} = \vec{A C};$

C. $\vec{A B} + \vec{A D} + \vec{A A'} = \vec{A C'};$

D. $\vec{A B} + \vec{A D} + \vec{A A'} = \vec{B C} .$

Xem đáp án

Cho hình hộp ABCD.A’B’C’D’ chọn khẳng định đúng (ảnh 1)

Câu 6:

Gọi φ là góc giữa 2 đường thẳng trong không gian. Chọn khẳng định đúng:

A. 0° < φ < 180°;

B. 0° £ φ £ 90°;

C. 0° < φ < 90°;

D. 0° £ φ £ 180

Xem đáp án

Đáp án đúng là: B

Theo đề bài, φ là góc giữa 2 đường thẳng trong không gian.

Do đó số đo của φ thỏa mãn 0° £ φ £ 90°.

Câu 7:

Trong không gian cho hai vectơ $\vec{u}$ và $\vec{v}$ . Chọn mệnh đề đúng.

A. $\vec{u} . \vec{v} = |\vec{u}| |\vec{v}| \cos (\vec{v}, \vec{u});$

B. $\vec{u} . \vec{v} = |\vec{u}| |\vec{v}| \sin (\vec{u}, \vec{v});$

C. $\vec{u} . \vec{v} = \vec{u} . \vec{v} \cos (\vec{u}, \vec{v});$

D. $\vec{u} . \vec{v} = \vec{u} . \vec{v} \tan (\vec{u}, \vec{v}) .$

Xem đáp án

Đáp án đúng là: A

Trong không gian cho hai vectơ và . Tích vô hướng của 2 véc-tơ là:

$\vec{u} . \vec{v} = |\vec{u}| |\vec{v}| \cos (\vec{v}, \vec{u}) .$

Câu 8:

Tính $\lim_{x \to - 8} \frac{x^{2} + 7 x - 8}{x + 8}$

A. 0

B. -7;

C. 9;

D. -9

Xem đáp án

Câu 9:

Phương trình tiếp tuyến của đường cong y = f (x) tại điểm M₀(x₀; y₀) là

A. y - y₀ = f (x₀)(x - x₀);

B.

y = f^{'} (x_{0}) (x + x_{0}) + y_{0};

C.

y + y_{0} = f^{'} (x_{0}) (x - x_{0});

D.

y = f^{'} (x_{0}) (x - x_{0}) + y_{0} .

Xem đáp án

Đáp án đúng là: D

Phương trình tiếp tuyến của đường cong y = f (x) tại điểm M₀(x₀; y₀) là

Câu 10:

Tính tổng $S = 1 + \frac{1}{3} + \frac{1}{9} + \cdot \cdot \cdot + \frac{1}{3^{n - 1}} .$

A. 1

B. $\frac{3}{2};$

C. $\frac{1}{9};$

D. $\frac{3}{4};$

Xem đáp án

Tính tổng S= = 1+1/3+1/9+...+1/3^n-1 (ảnh 1)

Câu 11:

Cho hàm số

y = \frac{2 x + 1}{x - 1}

chọn mệnh đề đúng

A. $\lim_{x \to 1^{+}} y = 3;$

B. $\lim_{x \to 1^{+}} y = 0;$

C. $\lim_{x \to 1^{+}} y = - \infty;$

D. $\lim_{x \to 1^{+}} y = + \infty .$

Xem đáp án

Cho hàm số y= 2x+1/x-1 chọn mệnh đề đúng (ảnh 1)

Câu 12:

Hãy cho biết mệnh đề nào sau đây là sai? Hai đường thẳng vuông góc nếu:

A. góc giữa hai vectơ chỉ phương của chúng là 90°;

B. tích vô hướng giữa hai vectơ chỉ phương của chúng là bằng 0;

C. góc giữa hai vectơ chỉ phương của chúng là 0°;

D. góc giữa hai đường thẳng đó là 90°.

Xem đáp án

Đáp án đúng là: C

Hai đường thẳng vuông góc nếu góc giữa hai vectơ chỉ phương của chúng là 90°. Vậy nên phương án C là sai.

Câu 13:

Chọn đáp án đúng:

A. $\lim {(\frac{1}{3})}^{n} = 3;$

B. $\lim \frac{2}{n + 2} = 2;$

C. $\lim \frac{1}{n} = 1;$

D. $\lim \frac{1}{n} = 0.$

Xem đáp án

Chọn đáp án đúng: A. lim 1/3^n=3 (ảnh 1)

Câu 14:

Tính $\lim \frac{n + 3}{2 n - 1}$

A. -3

B. $- \frac{1}{3};$

B. 2

D. $\frac{1}{2} .$

Xem đáp án

Câu 15:

Hàm số nào liên tục trên ℝ

A. y = tan x;

B. y = -x³ + 3x² - x + 1;

C.

y = \frac{x + 1}{x - 2};

D. y = cot x.

Xem đáp án

Đáp án đúng là: B

+) y = tan x có tập xác định là cos x ¹ 0 nên không liên tục trên ℝ;

+) y = -x³ + 3x² - x + 1 là hàm đa thức nên liên tục trên ℝ;

+) $y = \frac{x + 1}{x - 2}$ có tập xác định là x - 2 ¹ 0 nên không liên tục trên ℝ;

+) y = cot x có tập xác định là sin x ¹ 0 nên không liên tục trên ℝ.

Câu 16:

Cho tứ diện đều ABCD khi đó góc giữa hai đường thẳng AB và AC là

A. 45°;

B. 60°;

C. 90°;

D. 120°.

Xem đáp án

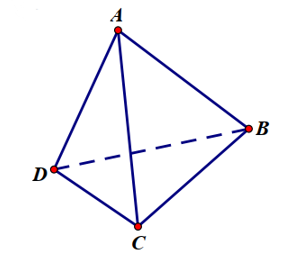
Đáp án đúng là: B

Góc giữa hai đường thẳng AB và AC là $\hat{B A C} = 60 ° .$

Câu 17:

Đạo hàm của hàm số y = x² tại điểm x₀ = 3 là

A. 3;

B. 0;

C. 4;

D. 6

Xem đáp án

Đáp án đúng là: D

Ta có y = x²

Suy ra y' = 2x.

Vậy tại x₀ = 3 thì đạo hàm của hàm số là 2.3 = 6.

Câu 18:

Cho hình lập phương ABCD.A’B’C’D’. Hãy xác định góc giữa cặp vectơ $\vec{A B}$ và $\vec{D D_{1}}$ ?

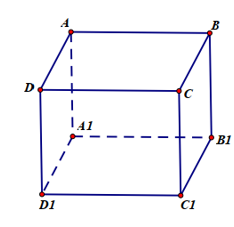
Cho hình lập phương ABCD.A’B’C’D’. Hãy xác định góc giữa cặp vectơ và ? (ảnh 1)

A. 60°;

B. 90°;

C. 120°;

D. 45°.

Xem đáp án

Đáp án đúng là: B

Ta có DD₁ ^ (ABCD) nên DD₁ ^ AB.

Vậy nên góc giữa cặp vectơ và là 90°.

Câu 19:

Chọn đáp án đúng:

A. $\lim_{x \to 1} 5 = 1;$

B. $\lim_{x \to 2} (2 x) = 2;$

C. $\lim_{x \to 2} x^{4} = - \infty;$

D. $\lim_{x \to + \infty} x^{3} = + \infty .$

Xem đáp án

Chọn đáp án đúng: A. lim x đến 1 5=1 (ảnh 1)

Câu 20:

Hàm số nào gián đoạn tại x₀ = 2.

A. $y = \frac{x + 1}{x - 2};$

B. $y = \frac{x - 1}{x};$

C. $y = \frac{x - 2}{x + 1};$

D. $y = \frac{x + 1}{x + 2} .$

Xem đáp án

Đáp án đúng là: A

Ta có $y = \frac{x + 1}{x - 2}$ có tập xác định là x ¹ 2.

Do đó hàm số gián đoạn tại x₀ = 2.

Câu 21:

Tính Các Giới hạn sau.

a. $\lim \frac{n^{2} + 3 n}{n^{2} - 2 n},$

b. $\lim \frac{{2.3}^{n} + {4.4}^{n}}{{3.2}^{n} + {5.4}^{n}};$

c. $\lim_{x \to 2} (x^{2} + 3 x - 2) .$

Xem đáp án

Câu 22:

a) Chứng minh phương trình x⁵ + 4x³ - x² - 1 = 0 có ít nhất một nghiệm thuộc khoảng (0; 1).

b) Tính $\lim_{x \to 3} \frac{\sqrt{x - 2} - 1}{x - 3} .$

c) Xét tính liên tục của hàm số

f (x) = \{\begin{matrix} \frac{x^{2} + x - 2}{x^{2} - 1} k h i x < 1 \\ \frac{3}{2} x k h i x \geq 1 \end{matrix}

tại x = 1.

Xem đáp án

a) Xét hàm số f (x) = x⁵ + 4x³ - x² - 1 là hàm liên tục

b) trên ℝ nên cũng liên tục trên khoảng (0; 1) (1)

Ta có: f(0) = –1; f(1) = 1 + 4 – 1 = 3

Do đó f (0).f (1) = (-1).3 = -3 < 0 (2)

Từ (1) và (2) suy ra phương trình f (x) = 0 cho ít nhất

một nghiệm x thuộc khoảng (0; 1).

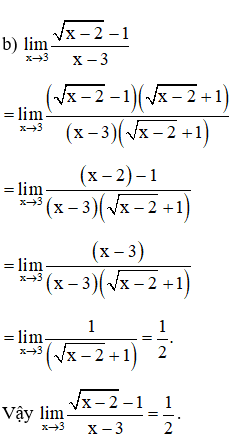
Chứng minh phương trình x5 + 4x3  x2  1 = 0 có ít nhất một nghiệm thuộc khoảng (0; 1). (ảnh 1)

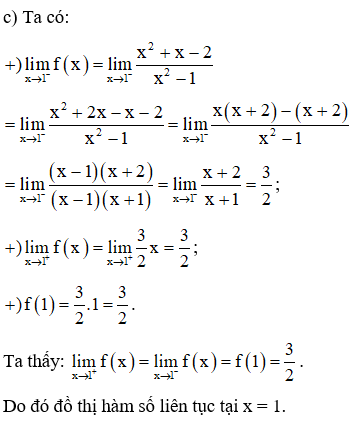
Câu 23:

Cho tam giác đều A₁B₁C₁ có cạnh bằng a và có diện tích bằng S₁. Nối các trung điểm của các cạnh tam giác A₁B₁C₁ ta được tam giác A₂B₂C₂ có diện tích là S₂ tiếp tục như thế ta được dãy các tam giác. Tính a biết $S_{1} + S_{2} + S_{3} + ... = \frac{\sqrt{3}}{3}$ .

Xem đáp án

Tỉ số diện tích của hai tam giác đồng dạng thì bằng bình phương tỉ số đồng dạng (1)

Công thức tính diện tích tam giác đều là:

(với x là độ dài cạnh tam giác) (2)

Từ (1) và (2) suy ra được:

; $S_{1} = \frac{a^{2} \sqrt{3}}{4} S_{2} = \frac{1}{2^{2}} . S_{1} = \frac{1}{2^{2}} . \frac{a^{2} \sqrt{3}}{4} = \frac{a^{2} \sqrt{3}}{16} S_{2} = \frac{1}{2^{2}} . S_{2} = \frac{1}{2^{2}} . \frac{a^{2} \sqrt{3}}{16} = \frac{a^{2} \sqrt{3}}{64}$

.

Ta thấy S₁, S₂, S₃,..., là các số hạng của một cấp số nhân lùi vô hạn có số hạng thứ nhất là $u_{1} = S_{1} = \frac{a^{2} \sqrt{3}}{4}$ và công bội $q = \frac{1}{2^{2}} = \frac{1}{4}$ .

Do đó

.

$S = S_{1} . \frac{q^{n} - 1}{q - 1} = \frac{a^{2} \sqrt{3}}{4} \cdot \frac{{(\frac{1}{4})}^{n} - 1}{\frac{1}{4} - 1}$ ;

$= \frac{a^{2} \sqrt{3}}{4} \cdot \frac{- 1}{\frac{1}{4} - 1} = \frac{a^{2} \sqrt{3}}{3}$

Mà $S = S_{1} + S_{2} + S_{3} + ... = \frac{\sqrt{3}}{3}$

Do đó $\frac{a^{2} \sqrt{3}}{3} = \frac{\sqrt{3}}{3} \Leftrightarrow a = 1.$

Vậy a = 1.

Câu 24:

Cho hình chóp S.ABCD có tất cả các cạnh bên đều bằng a và ASD = ASB.

a. Rút gọn $P = \vec{A B} - \vec{S B} + \vec{S D} - \vec{A C} + \vec{D C}$

b. Chứng minh rằng SA ^ BD

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 14)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương