25 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 21)

Câu 1:

$\lim \frac{4 n + 2019}{2 n + 1}$ bằng

A. 4

B. 2

C. 2019

D. $\frac{1}{2}$

Xem đáp án

Ta có $\lim \frac{4 n + 2018}{2 n + 1} = \lim \frac{4 + \frac{2018}{n}}{2 + \frac{1}{n}} = 2$

Câu 2:

Cho tứ diện ABCD có G là trọng tâm. Khẳng định nào sau đây đúng?

A. $G A = G B = G C = G D$

B. $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0}$

C. $\vec{G A} = \vec{G B} = \vec{G C} = \vec{G D}$

D. $G A + G B + G C + G D = 0$

Xem đáp án

Lời giải

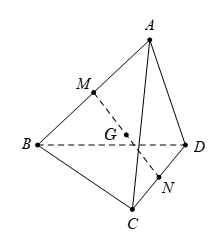
Cho tứ diện ABCD có G là trọng tâm. Khẳng định nào sau đây đúng? (ảnh 1)

Gọi M, N lần lượt là trung điểm của AB, CD.

Khi đó ta có G là trung điểm của MN và:

$\vec{G A} + \vec{G B} = 2 \vec{G M}$

$\vec{G C} + \vec{G D} = 2 \vec{G N}$

Cộng hai vế tương ứng ta được

\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = 2 \vec{G M} + 2 \vec{G N} = \vec{0}

.

Câu 3:

$\lim_{x \to + \infty} (x^{3} - 2019 x - 2020)$ bằng

A. 0

B. 1

C. $- \infty$

D. $+ \infty$

Xem đáp án

Lời giải

Ta có: $\lim_{x \to + \infty} (x^{3} - 2019 x - 2020) = \lim_{x \to + \infty} x^{3} (1 - \frac{2019}{x^{2}} - \frac{2020}{x^{3}})$ .

Vì $\lim_{x \to + \infty} x^{3} = + \infty$ và $\lim_{x \to + \infty} (1 - \frac{2019}{x^{2}} - \frac{2020}{x^{3}}) = 1 > 0$

nên theo quy tắc 2, $\lim_{x \to + \infty} (x^{3} - 2 x + 1) = + \infty$ .

Câu 4:

$\lim u_{n}$ , với $u_{n} = \frac{5 n^{2} + 3 n - 7}{n^{2}}$ bằng

A. 0

B. 5

C. 3

D. -7

Xem đáp án

Ta có $\lim u_{n} = \lim (\frac{5 n^{2}}{n^{2}} + \frac{3 n}{n^{2}} - \frac{7}{n^{2}}) = \lim (5 + \frac{3}{n} - \frac{7}{n^{2}}) = 5$

Câu 5:

Cho tứ diện ABCD. Gọi M là trung điểm của BC, biết $\vec{A B} = \vec{a}$ , $\vec{A C} = \vec{b}$ và $\vec{A D} = \vec{c}$ . Đẳng thức nào sau đây đúng?

A. $\vec{D M} = \frac{1}{2} (\vec{a} + \vec{c} - 2 \vec{b})$

B.. $\vec{D M} = \frac{1}{2} (\vec{b} + \vec{c} - 2 \vec{a})$

C. $\vec{D M} = \frac{1}{2} (\vec{a} + \vec{b} - 2 \vec{c})$

D. $\vec{D M} = \frac{1}{2} (\vec{a} + \vec{b} - \vec{c})$

Xem đáp án

Ta có $\vec{D M} = \frac{1}{2} (\vec{D B} + \vec{D C}) = \frac{1}{2} (\vec{D A} + \vec{A B} + \vec{D A} + \vec{A C}) = \frac{1}{2} (\vec{A B} + \vec{A C} - 2 \vec{A D}) = \frac{1}{2} (\vec{a} + \vec{b} - 2 \vec{c})$

Câu 6:

$\lim \frac{3^{n} - {4.2}^{n - 1} - 3}{{3.2}^{n} + 4^{n}}$ bằng

A. $+ \infty$

B. $- \infty$

C. 0

D. 1

Xem đáp án

$\lim \frac{3^{n} - {4.2}^{n - 1} - 3}{{3.2}^{n} + 4^{n}} = \lim \frac{3^{n} - {2.2}^{n} - 3}{{3.2}^{n} + 4^{n}} = \lim \frac{{(\frac{3}{4})}^{n} - 2. {(\frac{2}{4})}^{n} - 3. {(\frac{1}{4})}^{n}}{3. {(\frac{2}{4})}^{n} + 1} = 0$

Câu 7:

Cho hàm số $f (x) = x^{3} - 3 x^{2} + 1$ . Giá trị $\lim_{x \to - \infty} f (x)$ bằng

A. -3

B. $+ \infty$

C. 3

D. $- \infty$

Xem đáp án

Lời giải

Ta có: $\lim_{x \to - \infty} f (x) = \lim_{x \to - \infty} (x^{3} - 3 x^{2} + 1) = \lim_{x \to - \infty} x^{3} (1 - \frac{3}{x} + \frac{1}{x^{3}})$ .

Do $\lim_{x \to - \infty} x^{3} = - \infty$ và $\lim_{x \to - \infty} (1 - \frac{3}{x} + \frac{1}{x^{3}}) = 1$ nên $\lim_{x \to - \infty} f (x) = - \infty$ .

Câu 8:

$\lim_{x \to - \infty} \frac{3 \sqrt{x^{2} - 2}}{x}$ bằng

A. $- \infty$

B. $+ \infty$

C. 3

D. -3

Xem đáp án

Ta có $\lim_{x \to - \infty} \frac{3 \sqrt{x^{2} - 2}}{x} = \lim_{x \to - \infty} \frac{3 |x| \sqrt{1 - \frac{2}{x^{2}}}}{x} = \lim_{x \to - \infty} \frac{- 3 x \sqrt{1 - \frac{2}{x^{2}}}}{x} = \lim_{x \to - \infty} (- 3 \sqrt{1 - \frac{2}{x^{2}}}) = - 3$

Câu 9:

$\lim_{x \to 1^{+}} \frac{3 x - 4}{x - 1}$ bằng

A. $+ \infty$

B. -4

C. 3

D. $- \infty$

Xem đáp án

Lời giải

Ta có: $\lim_{x \to 1^{+}} (3 x - 4) = - 1, \lim_{x \to 1^{+}} (x - 1) = 0$ và $x - 1 > 0, \forall x > 1$ (do $x \to 1^{+}$ )

Do đó $\lim_{x \to 1^{+}} \frac{3 x - 4}{x - 1} = - \infty$ .

Câu 10:

Hàm số nào sau đây gián đoạn tại x=1?

A. $y = \frac{2 x + 1}{x^{2} + 1}$

B. $y = x^{3} + x + 1$

C. $y = \frac{x}{x^{2} - 1}$

D. $y = \sin x$

Xem đáp án

Lời giải

Xét hàm số $y = \frac{x}{x^{2} - 1}$ , hàm số này không xác định tại $x = 1$ . Do đó hàm số gián đoạn tại x=1.

Câu 11:

Cho hình hộp

A B C D . A_{1} B_{1} C_{1} D_{1}

. Đẳng thức nào sau đây sai ?

A. $\vec{A C_{1}} + \vec{A_{1} C} = 2 \vec{A C}$

B. $\vec{A C_{1}} + \vec{C A_{1}} + 2 \vec{C_{1} C} = \vec{0}$

C. $\vec{C A_{1}} + \vec{A C} = \vec{C C_{1}}$

D. $\vec{A C_{1}} + \vec{C D} = \vec{A_{1} D_{1}}$

Xem đáp án

Lời giải

+ $\vec{A C_{1}} + \vec{A_{1} C} = \vec{A C} + \vec{C C_{1}} + \vec{A_{1} A} + \vec{A C} = 2 \vec{A C}$ .

+ $\vec{A C_{1}} + \vec{C A_{1}} + 2 \vec{C_{1} C} = \vec{A C_{1}} + \vec{C_{1} C} + \vec{C A_{1}} + \vec{C_{1} C} = \vec{A C} + \vec{C_{1} A_{1}} = \vec{0}$ .

+ $\vec{C A_{1}} + \vec{A C} = \vec{A A_{1}} = \vec{C C_{1}}$ .

+ $\vec{A C_{1}} + \vec{C D} = \vec{A C_{1}} + \vec{C_{1} D_{1}} = \vec{A D_{1}}$ .

Câu 12:

Tính

\lim (- 2 n^{3} + 2 n^{} + 1)

A. $+ \infty$

B. 2

C. -2

D. $- \infty$

Xem đáp án

Lời giải

$\lim (- 2 n^{3} + 2 n^{} + 1) = \lim n^{3} (- 2 + \frac{2}{n^{2}} + \frac{1}{n^{3}})$ .

Vì $\lim n^{3} = + \infty$ và $\lim (- 2 + \frac{2}{n^{2}} + \frac{1}{n^{3}}) = - 2$ nên $\lim (- 2 n^{3} + 2 n^{} + 1) = - \infty$ .

Câu 13:

Cho tứ diện ABCD có AB=AC=AD và $\hat{B A C} = \hat{B A D} = 60 °$ . Tính góc giữa hai đường thẳng AB và CD.

A. $30 °$

B. 45 $°$

C. 60 $°$

D. 90 $°$

Xem đáp án

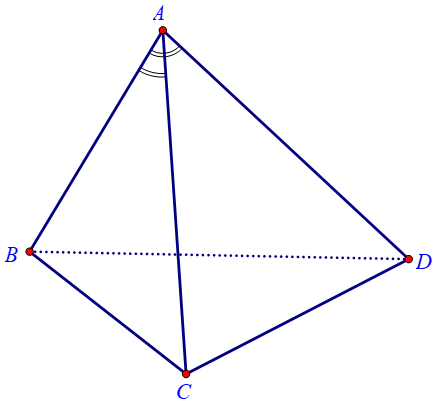
Cho tứ diện ABCD có AB=AC=AD và góc BAC= góc BAD =60 độ Tính góc giữa hai đường thẳng AB và CD. (ảnh 1)

Ta có $\vec{A B} . \vec{C D} = \vec{A B} . (\vec{A D} - \vec{A C}) = A B . A D . \cos \hat{B A D} - A B . A C . \cos \hat{B A C} = 0$ .

Do đó $\vec{A B} ⊥ \vec{C D}$ , tức $A B ⊥ C D$ . Vậy $(A B, C D) = 90^{0}$ .

Câu 14:

Tính

I = \lim (\sqrt{n^{2} - 2 n + 3} - n)

A. I=1

B. I=-1

C. I=0

D. I= $+ \infty$

Xem đáp án

Ta có $I = \lim (\sqrt{n^{2} - 2 n + 3} - n)$ $= \lim \frac{(\sqrt{n^{2} - 2 n + 3} - n) (\sqrt{n^{2} - 2 n + 3} + n)}{\sqrt{n^{2} - 2 n + 3} + n}$ $= \lim \frac{(n^{2} - 2 n + 3) - n^{2}}{\sqrt{n^{2} - 2 n + 3} + n}$

$= \lim \frac{- 2 n + 3}{\sqrt{n^{2} - 2 n + 3} + n}$ $= \lim \frac{- 2 + \frac{3}{n}}{\sqrt{1 - \frac{2}{n} + \frac{3}{n^{2}}} + 1} = \frac{- 2}{\sqrt{1} + 1} = - 1.$

Câu 15:

Cho hình chóp SABC có đáy là tam giác cân tại A,SA vuông góc với đáy, M là trung điểm của BC, J là trung điểm của BM. Khẳng định nào sau đây đúng?

A. $B C ⊥ (S A M)$

B. $B C ⊥ (S A C)$

C. $B C ⊥ (S A B)$

D. $B C ⊥ (S A J)$

Xem đáp án

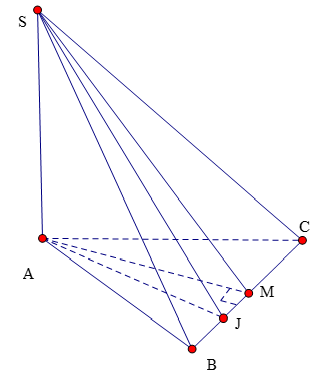
Cho hình chóp SABC có đáy là tam giác cân tại A,SA vuông góc với đáy, M là trung điểm của BC, J là trung điểm của BM. Khẳng định nào sau đây đúng? (ảnh 1)

Ta có $S A ⊥ (A B C)$ $\Rightarrow S A ⊥ B C (1)$ .

$Δ A B C$ cân tại $A \Rightarrow$ $A M ⊥ B C (2)$ .

Từ (1) và (2) suy ra $B C ⊥ (S A M)$ .

Câu 16:

Hàm số $f (x) = \frac{x + 1}{x^{2} - 5 x + 4}$ liên tục trên khoảng nào sau đây?

A. $(- \infty; 4)$

B. $(- 1; 2)$

C. $[1; + \infty)$

D. $(2; 3)$

Xem đáp án

Lời giải

Ta có f(x) là hàm số phân thức hữu tỉ có tập xác định là $D = ℝ \ \{1; 4\}$ nên f(x) liên tục trên các khoảng $(- \infty; 1), (1; 4), (4; + \infty)$ .

Do đó f(x) liên tục trên (2,3).

Câu 17:

Cho hình chóp SABC đáy ABC là tam giác đều, SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của AB và SB. Mệnh đề nào sau đây sai?

A. $C M ⊥ S B$

B. $N C ⊥ A B$

C. $A N ⊥ B C$

D. $M N ⊥ M C$

Xem đáp án

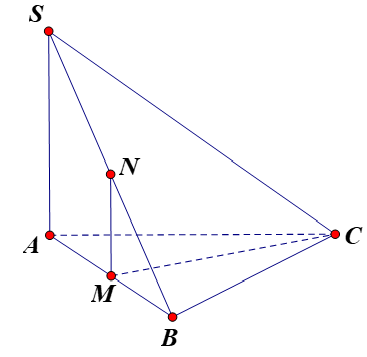
Cho hình chóp SABC đáy ABC là tam giác đều, SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của AB và SB. (ảnh 1)

Ta có: $S A ⊥ (A B C)$ $\Rightarrow S A ⊥ C M$ (1)

$Δ A B C$ đều $\Rightarrow A B ⊥ C M$ (2)

Từ (1) và (2) ta có $C M ⊥ (S A B)$ . Tức $C M ⊥ S B$ , $C M ⊥ M N$ .

Lại có: $M N / / S A \Rightarrow$ $M N ⊥ (A B C) \Rightarrow$ $M N ⊥ A B$ (3)

Từ (2) và (3) ta có $A B ⊥ (C M N)$ . Tức $A B ⊥ N C$ .

Giả sử $A N ⊥ B C$ . Do $S A ⊥ (A B C)$ $\Rightarrow A S ⊥ B C$ nên $B C ⊥ (S A B)$ , dẫn đến $B C ⊥ A B$ , vô lý. Do đó điều giả sử là sai.

Câu 18:

Tìm tất cả các giá trị của tham số m để hàm số

$f (x) = \{\begin{cases} \frac{\sqrt{1 - x} - \sqrt{1 + x}}{x} khi x < 0 \\ m + \frac{1 - x}{1 + x} khi x \geq 0 \end{cases}$ liên tục tại x=0

A. m=1

B. m=-2

C. m= -1

D.m= 0

Xem đáp án

Lời giải

Ta có: $\lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{+}} (m + \frac{1 - x}{1 + x}) = m + 1$

$\lim_{x \to 0^{-}} f (x) = \lim_{x \to 0^{-}} (\frac{\sqrt{1 - x} - \sqrt{1 + x}}{x})$ = $\lim_{x \to 0^{-}} (\frac{- 2 x}{x (\sqrt{1 - x} + \sqrt{1 + x})})$ = $\lim_{x \to 0^{-}} (\frac{- 2}{(\sqrt{1 - x} + \sqrt{1 + x})})$ =-1

f (0) = m + 1

f(x) liên tục tại x=0 khi và chỉ khi $\lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{-}} f (x) = f (0) \Leftrightarrow m + 1 = - 1 \Rightarrow m = - 2$ .

Câu 19:

Cho hai dãy

(u_{n}), (v_{n})

thỏa mãn

v_{n} = u_{n + 1} - u_{n}

,

\forall n \geq 1

, trong đó

u_{1} = 1

và

(v_{n})

là cấp số cộng có

v_{1} = 3

, công sai là 3. Đặt

S_{n} = u_{1} + u_{2} + ... + u_{n}

. Tính

\lim \frac{S_{n}}{n^{3}}

.

A. $+ \infty$

B. $\frac{3}{4}$

C. 1

D. $\frac{1}{2}$

Xem đáp án

Lời giải

Ta có: $v_{n} = v_{1} + (n - 1) d$ = $3 + 3 (n - 1) = 3 n$

Do $u_{n} = (u_{n} - u_{n - 1}) + (u_{n - 1} - u_{n - 2}) + ... + (u_{2} - u_{1}) + u_{1}$ = $v_{n - 1} + v_{n - 2} + ... + v_{1} + 1$ .

Nên $u_{n}$ $3 [(n - 1) + (n - 2) + ... + 1] + 1$ $\frac{3 n (n - 1)}{2} + 1$ $= \frac{3 n^{2} - 3 n + 2}{2}$ $\frac{3}{2} n^{2} - \frac{3}{2} n + 1$

Từ đó ta có: $u_{1} + u_{2} + u_{3} + ... + u_{n}$ $\frac{3}{2} (1^{2} + 2^{2} + ... + n^{2}) - \frac{3}{2} (1 + 2 + ... + n) + n .1$

$= \frac{3}{2} \frac{n (n + 1) (2 n + 1)}{6} - \frac{3}{2} \frac{n (n + 1)}{2} + n$ = $\frac{n^{3} + n}{2}$

$\Rightarrow$ $\lim \frac{S_{n}}{n^{3}} = \lim (\frac{1}{2} + \frac{1}{2 n^{2}}) = \frac{1}{2}$ .

Câu 20:

Biết rằng $\lim_{x \to 0} \frac{\sqrt[2019]{1 + 2020 x} - 1}{x} = \frac{a}{b}$ với a, b $\in Z$ , b>0 và $\frac{a}{b}$ là phân số tối giản. Tính a-b.

A. 2019

B. 2020

C. -1

D. 1

Xem đáp án

Lời giải

Đặt $y = \sqrt[2019]{1 + 2020 x}$ . Do $x \to 0$ nên $y \to 1$ .

Ta có $\lim_{x \to 0} \frac{\sqrt[2019]{1 + 2020 x} - 1}{x}$ = $2020. \lim_{y \to 1} \frac{y - 1}{y^{2019} - 1}$ $2020. \lim_{y \to 1} \frac{y - 1}{(y - 1) (y^{2018} + y^{2017} + ... + y + 1)}$

$2020. \lim_{y \to 1} \frac{1}{y^{2018} + y^{2017} + ... + y + 1}$ = $\frac{2020}{2019}$ .

Tức $a = 2020$ , $b = 2019$ . Vậy $a - b = 2020 - 2019 = 1$ .

Câu 21:

Xét tính liên tục của hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 1}{x - 1} khi x \neq 1 \\ 2 khi x = 1 \end{cases}$ trên tập xác định của nó.

Xem đáp án

Lờigiải

Hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 1}{x - 1} khi x \neq 1 \\ 2 khi x = 1 \end{cases}$ có tập xác định là R.

+ Với mọi $x \in (- \infty; 1)$ thì $f (x) = \frac{x^{2} - 1}{x - 1}$

Ta có: $\forall x_{0} \in (- \infty; 1)$ , $\lim_{x \to x_{0}} f (x) = \lim_{x \to x_{0}} \frac{x^{2} - 1}{x - 1} = \frac{x_{0}^{2} - 1}{x_{0} - 1} = f (x_{0})$

Nên hàm số f liên tục trên $(- \infty; 1)$ (1)

+ Với mọi $x \in (1; + \infty)$ thì $f (x) = \frac{x^{2} - 1}{x - 1}$

Ta có: $\forall x_{0} \in (1; + \infty)$ , $\lim_{x \to x_{0}} f (x) = \lim_{x \to x_{0}} \frac{x^{2} - 1}{x - 1} = \frac{x_{0}^{2} - 1}{x_{0} - 1} = f (x_{0})$

Nên hàm số f liên tục trên $(1; + \infty)$ (2)

+ Tại x=1:

Ta có $f (1) = 2$ và $\lim_{x \to 1} f (x)$ $= \lim_{x \to 1} \frac{x^{2} - 1}{x - 1}$ $= \lim_{x \to 1} (x + 1)$ =2

$\Rightarrow \lim_{x \to 1} f (x) = f (1)$

Tức hàm số f liên tục tại x=1 (3)

Từ (1), (2) và (3). Suy ra, hàm số f liên tục trên R.

Kết luận: Hàm số f liên tục trên R.

Câu 22:

Tính

\lim (\frac{1}{1.3} + \frac{1}{3.5} + \frac{1}{5.7} + ... + \frac{1}{(2 n - 1) (2 n + 1)})

Xem đáp án

Lờigiải

Ta có: $\frac{1}{(2 k - 1) . (2 k + 1)} = \frac{1}{2} (\frac{1}{2 k - 1} - \frac{1}{2 k - 1}), \forall k \in ℕ^{^{*}}$

Do đó: $\frac{1}{1.3} + \frac{1}{3.5} + \frac{1}{5.7} + ... + \frac{1}{(2 n - 1) (2 n + 1)}$

$= \frac{1}{2} (1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + \frac{1}{5} - \frac{1}{7} + ... + \frac{1}{2 n - 1} - \frac{1}{2 n + 1})$

$= \frac{1}{2} (1 - \frac{1}{2 n + 1}) = \frac{n}{2 n + 1}$ .

Nên $\lim (\frac{1}{1.3} + \frac{1}{3.5} + \frac{1}{5.7} + ... + \frac{1}{(2 n - 1) (2 n + 1)})$

$= lim \frac{n}{2 n + 1}$ $= lim \frac{n}{n (2 + \frac{1}{n})}$

$= lim \frac{1}{(2 + \frac{1}{n})} = \frac{1}{2 + 0} = \frac{1}{2}$ .

Kết luận: $\lim (\frac{1}{1.3} + \frac{1}{3.5} + \frac{1}{5.7} + ... + \frac{1}{(2 n - 1) (2 n + 1)}) = \frac{1}{2}$ .

Câu 23:

Tính

\lim_{x \to 0} \frac{\sqrt{2 x + 4} + \sqrt[3]{5 x + 8} - \sqrt{3 x + 1} - 3}{x^{2} + 3 x}

Xem đáp án

Lờigiải

Ta có:

$\frac{\sqrt{2 x + 4} + \sqrt[3]{5 x + 8} - \sqrt{3 x + 1} - 3}{x^{2} + 3 x}$

$= \frac{(\sqrt{2 x + 4} - 2) + (\sqrt[3]{5 x + 8} - 2) - (\sqrt{3 x + 1} - 1)}{(x + 3) x}$

$= \frac{2 x}{(\sqrt{2 x + 4} + 2) (x + 3) x} + \frac{5 x}{({(\sqrt[3]{5 x + 8})}^{2} + 2 \sqrt[3]{5 x + 8} + 2^{2}) (x + 3) x} - \frac{3 x}{(\sqrt{3 x + 1} + 1) (x + 3) x}$

$= \frac{2}{(\sqrt{2 x + 4} + 2) (x + 3)} + \frac{5}{({(\sqrt[3]{5 x + 8})}^{2} + 2 \sqrt[3]{5 x + 8} + 4) (x + 3)} - \frac{3}{(\sqrt{3 x + 1} + 1) (x + 3)}$

Do đó $\lim_{x \to 0} \frac{\sqrt{2 x + 4} + \sqrt[3]{5 x + 8} - \sqrt{3 x + 1} - 3}{x^{2} + 3 x}$

$= \lim_{x \to 0} (\frac{2}{(\sqrt{2 x + 4} + 2) (x + 3)} + \frac{5}{({(\sqrt[3]{5 x + 8})}^{2} + 2 \sqrt[3]{5 x + 8} + 4) (x + 3)} - \frac{3}{(\sqrt{3 x + 1} + 1) (x + 3)})$

$= \frac{2}{(2 + 2) 3} + \frac{5}{(4 + 4 + 4) 3} - \frac{3}{(1 + 1) 3}$

$= \frac{1}{6} + \frac{5}{36} - \frac{1}{2} = - \frac{7}{36}$ .

Kết luận: $\lim_{x \to 0} \frac{\sqrt{2 x + 4} + \sqrt[3]{5 x + 8} - \sqrt{3 x + 1} - 3}{x^{2} + 3 x} = - \frac{7}{36}$ .

Câu 24:

Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và B, $S A ⊥ (A B C D)$ , $A D = 2 a$ , $A B = B C = a$ . Chứng minh tam giác SCD là tam giác vuông.

Xem đáp án

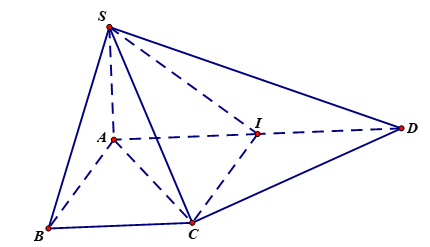
Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và B (ảnh 1)

Ta có :

\begin{array}{l} S A ⊥ (A B C D) \\ C D \subset (A B C D) \end{array}\} \Rightarrow S A ⊥ C D (1)

.

+ Gọi I là trung điểm của AD, khi đó ABCI là hình vuông. Do đó $C I = \frac{1}{2} A D$ nên tam giác ACD vuông tại C. Tức $A C ⊥ C D$ (2).

Từ (1) và (2) ta có

C D ⊥ S C

. Tức

Δ S C D

vuông tại C.

Câu 25:

Cho tứ diện ABCD. Lấy các điểm M,N,P,Q lần lượt thuộc AB, CD, DA sao cho $\vec{A M} = \frac{1}{3} \vec{A B}, \vec{B N} = \frac{2}{3} \vec{B C}, \vec{A Q} = \frac{1}{2} \vec{A D}$ và $\vec{D P} = k \vec{D C}$ . Tìm để bốn điểm $M, N, P, Q$ cùng nằm trên một mặt phẳng.

Xem đáp án

Giả sử M, N, P, Q đồng phẳng:

Ta có: (MNPQ) $\cap$ (BAC) = MN, (MNPQ) $\cap$ (DAC) = PQ, (BAC) $\cap$ (DAC) = AC.

Do MN, PQ, AC đôi một không trùng nhau và MN//AC nên PQ//AC. Từ đây có $k = \frac{1}{2}$ .

Thử lại, thấy

k = \frac{1}{2}

thỏa mãn.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 21)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương