39 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 5)

Câu 1:

Dãy số nào sau đây có giới hạn bằng 0?

A. $\frac{3 n^{2} + 11}{2 n + 3}$

B. $2 n - 5 n^{2}$

C. $\frac{5 n + 1}{2 n + 11}$

D. $\frac{3}{2 n + 1}$

Xem đáp án

Ta có $\lim \frac{3}{2 n + 1} = \lim \frac{\frac{3}{n}}{2 + \frac{1}{n}} = \frac{0}{2} = 0$

Chọn đáp án D.

Câu 2:

Dãy số nào sau đây có giới hạn khác 0?

A. $\frac{2 n + 3}{n + 5}$

B. $\frac{1}{3 n + 1}$

C. ${(\frac{3}{4})}^{2 n}$

D. $\frac{2 n + 1}{3 n^{2} + 1}$

Xem đáp án

Ta có $\lim \frac{2 n + 3}{n + 5} = \lim \frac{2 + \frac{3}{n}}{1 + \frac{5}{n}} = \frac{2}{1} = 2$

Chọn đáp án A.

Câu 3:

$\lim \frac{2 n + 1}{n^{3} + 7}$ bằng

A. 0.

B. –∞.

C. +∞.

D. 2.

Xem đáp án

Ta có $\lim \frac{2 n + 1}{n^{3} + 7} = \lim \frac{\frac{2}{n^{2}} + \frac{1}{n^{3}}}{1 + \frac{7}{n^{3}}} = \frac{0}{1} = 0$

Chọn đáp án A.

Câu 4:

$\lim (n^{2} - n + 5)$ bằng

A. 1.

B. –∞.

C. 0.

D. +∞.

Xem đáp án

Ta có $\lim (n^{2} - n + 5) = \lim [n^{2} (1 - \frac{1}{n} + \frac{5}{n^{2}})]$

Mà $\lim n^{2} = + \infty; \lim (1 - \frac{1}{n} + \frac{5}{n^{2}}) = 1 > 0$ $\Rightarrow \lim [n^{2} (1 - \frac{1}{n} + \frac{5}{n^{2}})] = + \infty$

Chọn đáp án D.

Câu 5:

Tính giới hạn lim v_n biết lim u_n = 2, $\lim \frac{u_{n}}{v_{n}} = 3$

A. $\lim_{} v_{n} = \frac{2}{3}$

B. $\lim_{} v_{n} = \frac{3}{2}$

C. lim v_n= 6.

D. lim v_n = 1.

Xem đáp án

${limv}_{n} = \lim \frac{u_{n}}{\frac{u_{n}}{v_{n}}} = \frac{{limu}_{n}}{\lim \frac{u_{n}}{v_{n}}} = \frac{2}{3}$

Chọn đáp án A.

Câu 6:

Dãy số nào sau đây có giới hạn bằng +∞?

A. ${(\frac{\sqrt{2}}{2})}^{n}$

B. ${(- 1,101)}^{n}$

C. ${(0,919)}^{n}$

D. ${(1,101)}^{n}$

Xem đáp án

Ta có $\lim {(1,101)}^{n} = + \infty$ do 1,101 > 1.

Chọn đáp án D.

Câu 7:

Trong bốn giới hạn sau, giới hạn nào bằng –∞?

A. $\lim {(\frac{1}{2})}^{n}$

B. $\lim \frac{1}{n^{2}}$

C. lim n³

D. $\lim (- n^{2})$

Xem đáp án

$\lim (- n^{2}) = - \lim n^{2} = - \infty$

Chọn đáp án D.

Câu 8:

Tính giới hạn

\lim_{x \to a} x^{2}

là

A. 2a.

B. a.

C. a².

D. a + 2.

Xem đáp án

Ta có: $\lim_{x \to a} x^{2} = a^{2}$

Chọn đáp án C.

Câu 9:

Tính $I = \lim_{x \to 1} (- x + 3)$

A. 0.

B. 2.

C. 4.

D. – 5.

Xem đáp án

Ta có $I = \lim_{x \to 1} (- x + 3) = - 1 + 3 = 2$

Chọn đáp án B.

Câu 10:

Tính $M = \lim_{x \to - \infty} (x^{4} + x + 3)$

A. 3.

B. –∞.

C. +∞.

D. –3.

Xem đáp án

Ta có $M = \lim_{x \to - \infty} (x^{4} + x + 3)$ $= \lim_{x \to - \infty} x^{4} (1 + \frac{1}{x^{2}} + \frac{3}{x^{3}})$ $= + \infty$

vì $\lim_{x \to - \infty} x^{4} = + \infty$ và $\lim_{x \to - \infty} (1 + \frac{1}{x^{2}} + \frac{3}{x^{3}}) = 1 > 0$

Chọn đáp án C.

Câu 11:

Tính $N = \lim_{x \to + \infty} \frac{- x + 2}{x + 1}$

A. 6.

B. 2.

C. 1.

D. – 1.

Xem đáp án

Ta có $N = \lim_{x \to + \infty} \frac{- x + 2}{x + 1}$ $= \lim_{x \to + \infty} \frac{- 1 + \frac{2}{x}}{1 + \frac{1}{x}}$ $= - 1$

Chọn đáp án D.

Câu 12:

Tính $N = \lim_{x \to 3^{+}} \frac{x + 2}{x - 3}$

A. –∞.

B. +∞.

C. 2.

D. –3.

Xem đáp án

Ta có $N = \lim_{x \to 3^{+}} \frac{x + 2}{x - 3} = + \infty$ vì $\lim_{x \to 3^{+}} (x + 2) = 3 + 2 = 5 > 0$ và $\lim_{x \to 3^{+}} (x - 3) = 0$ ; x – 3 > 0 khi $x \to 3^{+}$

Chọn đáp án B.

Câu 13:

Cho hai hàm số f(x), g(x) thỏa mãn

\lim_{x \to 0} f (x) = 1

và

\lim_{x \to 0} g (x) = + \infty

. Giá trị của

\lim_{x \to 0} [f (x) . g (x)]

bằng

A. 1.

B. –1.

C. –∞.

D. +∞.

Xem đáp án

Ta có: $\lim_{x \to 0} f (x) = 1$ và $\lim_{x \to 0} g (x) = + \infty$ , suy ra $\lim_{x \to 0} [f (x) . g (x)] = + \infty$

Chọn đáp án D.

Câu 14:

Hàm số

y = \frac{3}{x (x + 1) (x + 2)}

liên tục tại điểm nào dưới đây?

A. x = 0.

B. x = – 1.

C. x = – 2.

D. x = 3.

Xem đáp án

Ta có: Tập xác định của hàm số $y = \frac{3}{x (x + 1) (x + 2)}$ là $D = ℝ \ \{- 2; - 1; 0\}$ . Vậy hàm số đã cho liên tục trên các khoảng xác định của nó.

Suy ra hàm số liên tục tại điểm x = 3.

Chọn đáp án D.

Câu 15:

Hàm số

y = - \frac{1}{x}

gián đoạn tại điểm nào dưới đây?

A. x = 0.

B. x = 1.

C. x = –1.

D. x = 2.

Xem đáp án

Ta có: Tập xác định của hàm số $y = - \frac{1}{x}$ là $D = ℝ \ \{0\}$ . Suy ra hàm số gián đoạn tại điểm x = 0.

Chọn đáp án A.

Câu 16:

Cho hai đường thẳng a, b cắt nhau và mặt phẳng (α) cắt a. Ảnh của b qua phép chiếu song song lên (α) theo phương a là

A. một điểm.

B. một đường thẳng.

C. một đoạn thẳng.

D. một tia.

Xem đáp án

Ta có: a, b cắt nhau và mặt phẳng (α) cắt a. Suy ra ảnh của b qua phép chiếu song song lên (α) theo phương a là một đường thẳng.

Chọn đáp án B.

Câu 17:

Cho hình chóp S.ABCD, có bao nhiêu vectơ khác vectơ

\vec{0}

mà có điểm đầu và điểm cuối là các đỉnh của hình chóp.

A. 10.

B. 4.

C. 12.

D. 20.

Xem đáp án

Số vectơ khác vectơ $\vec{0}$ mà có điểm đầu và điểm cuối là các đỉnh của hình chóp là chỉnh hợp chập 2 của 5 phần tử. Vậy có $A_{5}^{2} = 20$ vectơ.

Chọn đáp án D.

Câu 18:

Cho hình lập phương ABCD.A'B'C'D'.

Đẳng thức nào sau đây sai?

A. $\vec{AB} = \vec{AD}$

B. $|\vec{AB}| = |\vec{BC}|$

C. $\vec{CB} + \vec{CD} = \vec{CA}$

D. $\vec{BA} + \vec{BC} + \vec{{BB}^{'}} = \vec{{BD}^{'}}$

Xem đáp án

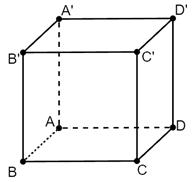
Hai vec tơ $\vec{AB}$ và $\vec{AD}$ là 2 vectơ không cùng phương nên chúng không bằng nhau.

Chọn đáp án A.

Câu 19:

Trong không gian cho điểm A và đường thẳng d. Có bao nhiêu đường thẳng qua A và vuông góc với đường thẳng d.

A. 0.

B. 1.

C. 2.

D. Vô số.

Xem đáp án

Có vô số đường thẳng qua A và vuông góc với đường thẳng d.

Chọn đáp án D.

Câu 20:

Trong không gian cho điểm A và đường thẳng ∆. Các đường thẳng qua A và vuông góc với đường thẳng ∆ thì

A. song song với nhau.

B. đồng phẳng.

C. cùng nằm trong một mặt phẳng chứa ∆.

D. vuông góc với nhau.

Xem đáp án

Các đường thẳng qua A và vuông góc với đường thẳng ∆ cùng nằm trong 1 mặt phẳng, mặt phẳng đó vuông góc với đường thẳng ∆.

Chọn đáp án B.

Câu 21:

Tìm

\lim \frac{2020 n^{2} - n}{2021 + n^{2}}

A. 2021.

B. 2022.

C. 4041.

D. 2020.

Xem đáp án

Chia tử số và mẫu số cho n², ta được $\frac{2020 n^{2} - n}{2021 + n^{2}} = \frac{2020 - \frac{1}{n}}{\frac{2021}{n^{2}} + 1}$

Vì $\lim (2020 - \frac{1}{n}) = \lim 2020 - \lim \frac{1}{n}$ $= 2020 - 0 = 2020$

Và $\lim (2021 . \frac{1}{n} \frac{1}{n} + 1)$ $= \lim 2021 . \lim \frac{1}{n} . \lim \frac{1}{n} + \lim 1$ $= 2021 .0.0 + 1 = 1$

Nên $\lim \frac{2020 n^{2} - n}{2021 + n^{2}} = \lim \frac{2020 - \frac{1}{n}}{\frac{2021}{n^{2}} + 1}$ $= \frac{\lim (2020 - \frac{1}{n})}{\lim (\frac{2021}{n^{2}} + 1)}$ $= \frac{2020}{1}$ $= 2020$

Vậy $\lim \frac{2020 n^{2} - n}{2021 + n^{2}} = 2020$

Chọn đáp án D.

Câu 22:

Tìm $\lim \frac{\sqrt{2 n + 5} - \sqrt{n}}{\sqrt{n}}$

A. $\sqrt{2} - 1$

B. $\sqrt{5}$

C. $\sqrt{2} + 1$

D. $\sqrt{2}$

Xem đáp án

Ta có: $\lim \frac{\sqrt{2 n + 5} - \sqrt{n}}{\sqrt{n}}$ = $\lim \frac{\sqrt{2 + \frac{5}{n}} - 1}{1}$ = $\sqrt{2} - 1$

Vậy $\lim \frac{\sqrt{2 n + 5} - \sqrt{n}}{\sqrt{n}}$ = $\sqrt{2} - 1$

Chọn đáp án A.

Câu 23:

Tính tổng

S = 1 - \frac{1}{5} + \frac{1}{25} - \frac{1}{125} + . .. + {(- \frac{1}{5})}^{n - 1} + . ..

A.

\frac{6}{5}

B. $\frac{4}{5}$

C. $\frac{5}{6}$

D. $\frac{5}{4}$

Xem đáp án

Các số hạng của tổng lập thành cấp số nhân lùi vô hạn với $u_{1} = 1$ , $q = - \frac{1}{5}$

Tổng của n số hạng đầu của cấp số nhân có $u_{1} = 1$ , $q = - \frac{1}{5}$ bằng:

$S_{n} = 1 - \frac{1}{5} + \frac{1}{25} - \frac{1}{125} + . .. + {(- \frac{1}{5})}^{n - 1}$ $= u_{1} . \frac{1 - q^{n}}{1 - q}$

Vì |q| < 1, do đó:

$S = 1 - \frac{1}{5} + \frac{1}{25} - \frac{1}{125} + . .. + {(- \frac{1}{5})}^{n - 1} + . .. = {limS}_{n} = \frac{u_{1}}{1 - q} = \frac{1}{1 - (- \frac{1}{5})} = \frac{5}{6}$

Vậy $S = \frac{5}{6}$

Chọn đáp án C.

Câu 24:

$\lim_{x \to 1} \frac{1 - x}{x^{2} + 3 x - 4}$ bằng

A. $\frac{1}{3}$

B. $\frac{1}{5}$

C. $- \frac{1}{3}$

D. $- \frac{1}{5}$

Xem đáp án

Ta có $\lim_{x \to 1} \frac{1 - x}{x^{2} + 3 x - 4}$ $= \lim_{x \to 1} \frac{1 - x}{(x - 1) (x + 4)}$ $= \lim_{x \to 1} \frac{- 1}{x + 4}$ $= - \frac{1}{5}$

Chọn đáp án D.

Câu 25:

$\lim_{x \to + \infty} \frac{x^{3} + 2 x^{2} + 1}{x^{2} + 3 x - 4}$ bằng

A. –∞.

B. +∞.

C. 1.

D. 0.

Xem đáp án

Ta có: $\lim_{x \to + \infty} \frac{x^{3} + 2 x^{2} + 1}{x^{2} + 3 x - 4} = \lim_{x \to + \infty} \frac{x^{3} (1 + \frac{2}{x} + \frac{1}{x^{3}})}{x^{2} (1 + \frac{3}{x} - \frac{4}{x^{2}})}$ $= \lim_{x \to + \infty} x . \lim_{x \to + \infty} \frac{1 + \frac{2}{x} + \frac{1}{x^{3}}}{1 + \frac{3}{x} - \frac{4}{x^{2}}}$

Vì $\{\begin{cases} \lim_{x \to + \infty} x = + \infty \\ \lim_{x \to + \infty} \frac{1 + \frac{2}{x} + \frac{1}{x^{3}}}{1 + \frac{3}{x} - \frac{4}{x^{2}}} = 1 \end{cases}$ nên $\lim_{x \to + \infty} \frac{x^{3} + 2 x^{2} + 1}{x^{2} + 3 x - 4} = + \infty$

Chọn đáp án B.

Câu 26:

$\lim_{x \to 2^{+}} \frac{2 x + 3}{2 - x}$ bằng

A. +∞.

B. 1.

C. –2.

D. –∞.

Xem đáp án

Ta có: $\{\begin{cases} \lim_{x \to 2^{+}} (2 x + 3) = 7 > 0 \\ \lim_{x \to 2^{+}} (2 - x) = 0 \\ 2 - x < 0 khi x \to 2^{+} \end{cases}$

Vậy: $\lim_{x \to 2^{+}} \frac{2 x + 3}{2 - x} = - \infty$

Chọn đáp án D.

Câu 27:

Cho hàm số

f (x) = \{\begin{cases} \frac{x^{2} - 4 x + 3}{x - 1} khi x > 1 \\ ax + 1 khi x \leq 1 \end{cases} .

Xác định số thực a để hàm số liên tục tại điểm x = 1

A. a = –1.

B. a = 1.

C. a = 3.

D. a = –3.

Xem đáp án

Tập xác định $D = ℝ .$

Ta có f(1) = a + 1

và $\lim_{x \to 1^{-}} f (x) = \lim_{x \to 1^{-}} (ax + 1) = a + 1;$ $\lim_{x \to 1^{+}} f (x) = \lim_{x \to 1^{+}} \frac{x^{2} - 4 x + 3}{x - 1}$ $= \lim_{x \to 1^{+}} (x - 3)$ $= - 2 .$

Hàm số đã cho liên tục tại $x = 1$ $\Leftrightarrow f (1) = \lim_{x \to 1^{-}} f (x) = \lim_{x \to 1^{+}} f (x)$ $\Leftrightarrow a + 1 = - 2 \Leftrightarrow a = - 3 .$

Chọn đáp án D.

Câu 28:

Cho hàm số $f (x) = \sqrt{x^{2} - \frac{1}{4}}$ . Chọn câu đúng trong các câu sau:

(I) f(x) liên tục tại $x = \frac{1}{2}$

(II) f(x) gián đoạn tại $x = \frac{1}{2}$ .

(III) f(x) liên tục trên đoạn $[- \frac{1}{2}; \frac{1}{2}]$ .

A. (I) và (III).

B. Chỉ (II).

C. (II) và (III).

D. Chỉ (I).

Xem đáp án

Ta có: $D = (- \infty; - \frac{1}{2}] \cup [\frac{1}{2}; + \infty)$

$\lim_{x \to {\frac{1}{2}}^{+}} f (x) = \lim_{x \to {\frac{1}{2}}^{+}} \sqrt{x^{2} - \frac{1}{4}} = 0$

Do không tồn tại $\lim_{x \to {\frac{1}{2}}^{-}} f (x)$ nên không tồn tại $\lim_{x \to \frac{1}{2}} f (x)$

Vậy hàm số gián đoạn tại $x = \frac{1}{2}$

Chọn đáp án B.

Câu 29:

Cho hàm số $f (x) = \{\begin{cases} \frac{\sqrt{3 x + 4} - \sqrt{2 x + 8}}{x - 4} khi x \neq 4 \\ a + 2 khi x = 4 \end{cases}$

Tìm tất cả các giá trị thực của tham số a để hàm số liên tục tại x₀ = 4.

A. a = 3.

B. $a = - \frac{15}{8}$

C. a = 2.

D. $a = \frac{5}{2}$

Xem đáp án

$\lim_{x \to 4} f (x) = \lim_{x \to 4} \frac{\sqrt{3 x + 4} - \sqrt{2 x + 8}}{x - 4}$

$= \lim_{x \to 4} \frac{(\sqrt{3 x + 4} - \sqrt{2 x + 8}) . (\sqrt{3 x + 1} + \sqrt{2 x + 8})}{(x - 4) . (\sqrt{3 x + 4} + \sqrt{2 x + 8})}$

$= \lim_{x \to 4} \frac{1}{(\sqrt{3 x + 4} + \sqrt{2 x + 8})} = \frac{1}{8}$

Hàm số liên tục tại $x_{0} = 4$ $\Leftrightarrow f (4) = \lim_{x \to 4} f (x)$ $\Leftrightarrow a + 2 = \frac{1}{8}$ $\Leftrightarrow a = - \frac{15}{8}$ .

Chọn đáp án B.

Câu 30:

Hàm số nào sau đây không liên tục trên

ℝ

?

A. $f (x) = 2 x + 3 \cos 2 (x + \frac{π}{4}) + 1$

B. $f (x) = \frac{2 x^{2} - x}{3 x^{2} + 4}$

C. $f (x) = {mx}^{2} + 2 x + 3$

D. $f (x) = \tan 2 x - 1$

Xem đáp án

Do hàm số f(x) = tan 2x – 1 có tập xác định là $D = ℝ \ \{\frac{π}{4} + k \frac{π}{2} / k \in ℤ\}$ nên hàm số không xác định trên $ℝ$ nên f(x) không liên tục trên $ℝ$ .

Chọn đáp án D.

Câu 31:

Cho tứ diện ABCD. Gọi G là trọng tâm tứ diện ABCD và G₀ là trọng tâm tam giác BCD. Khẳng định nào sau đây đúng?

A. $\vec{GA} = 3 \vec{{GG}_{0}}$

B. $\vec{{AG}_{0}} = 3 \vec{{GG}_{0}}$

C. $\vec{{AG}_{0}} = - 4 \vec{{GG}_{0}}$

D. $\vec{GA} = - 3 \vec{{GG}_{0}}$

Xem đáp án

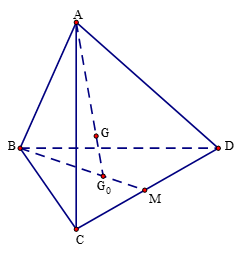
Cho tứ diện ABCD. Gọi G là trọng tâm tứ diện ABCD và G0 là trọng tâm tam giác BCD. Khẳng định nào sau đây đúng? (ảnh 1)

Do G là trọng tâm tứ diện ABCD nên ta có $\vec{GA} + \vec{GB} + \vec{GC} + \vec{GD} = \vec{0} .$

G₀ là trọng tâm tam giác BCD nên ta có $\vec{GB} + \vec{GC} + \vec{GD} = 3 \vec{{GG}_{0}} .$

Từ hai đẳng thức trên suy ra $\vec{GA} + 3 \vec{{GG}_{0}} = \vec{0} \Leftrightarrow \vec{GA} = - 3 \vec{{GG}_{0}} .$

Chọn đáp án D.

Câu 32:

Cho tứ diện đều ABCD cạnh bằng 2a. Tính tích vô hướng

\vec{AB} . \vec{CD}

:

A. 4a².

B. 2a².

C. –2a².

D. 0.

Xem đáp án

Ta có $\vec{AB} . \vec{CD} = \vec{AB} . (\vec{BD} - \vec{BC})$ $= \vec{AB} . \vec{BD} - \vec{AB} .$ $\vec{BC} = - \vec{BA} . \vec{BD} + \vec{BA} . \vec{BC}$

$= - 2 a . 2 a . \cos 60^{0} + 2 a . 2 a . \cos 60^{0} = 0$

Chọn đáp án D.

Câu 33:

Trong các mệnh đề sau, mệnh đề nào sai?

A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.

B. Hai đường thẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.

C. Một đường thẳng vuông góc với hai cạnh của tam giác thì sẽ vuông góc với cạnh thứ ba của tam giác đó.

D. Hai đường thẳng vuông góc nếu góc giữa hai véc tơ chỉ phương của chúng bằng 90°.

Xem đáp án

Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba có thể song song, cắt nhau hoặc chéo nhau.

Chọn đáp án A

Câu 34:

Cho tứ diện ABCD có AB = AC, DB = DC. Khẳng định nào sau đây đúng?

A. $AB ⊥ BC$

B. $AC ⊥ BD$

C. $AC ⊥ BC$

D. $BC ⊥ AD$

Xem đáp án

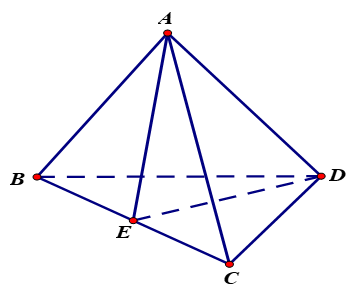
Cho tứ diện ABCD có AB = AC, DB = DC. Khẳng định nào sau đây đúng? (ảnh 1)

+ Gọi E là trung điểm của BC. Vì tam giác ABC cân tại A, tam giác DBC cân tại D nên ta có $AE ⊥ BC, DE ⊥ BC$ .

+ Do đó, $\vec{CB} . \vec{AD} = \vec{CB} . (\vec{AE} + \vec{ED}) = 0$ , nên $BC ⊥ AD$ .

Chọn đáp án D.

Câu 35:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó góc giữa A'C' và BD bằng

A. 0°.

B. 45°.

C. 60°.

D. 90°.

Xem đáp án

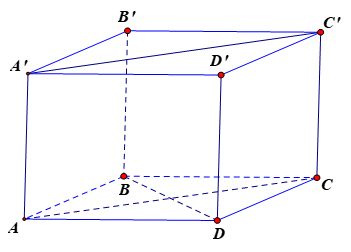
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó góc giữa A'C' và BD bằng (ảnh 1)

Vì $AC / / A^{'} C^{'}$ $\Rightarrow (A^{'} C^{'}; BD) = (AC; BD) = 90 °$ (tính chất hai đường chéo của hình vuông).

Chọn đáp án D.

Câu 36:

Tính $I = \lim \frac{\sqrt{2 + 4 + . .. + 2 n} + n}{\sqrt[3]{48 (1^{2} + 2^{2} + . .. + n^{2})} + 2 n}$ ?

Xem đáp án

Ta có $I = \lim \frac{\sqrt{2 + 4 + . .. + 2 n} + n}{\sqrt[3]{48 (1^{2} + 2^{2} + . .. + n^{2})} + 2 n}$ $= \lim \frac{\sqrt{2 (1 + 2 + . .. + n)} + n}{\sqrt[3]{48 (1^{2} + 2^{2} + . .. + n^{2})} + 2 n}$

Mà $1 + 2 + . .. + n = \frac{n (n + 1)}{2}$ ; $1^{2} + 2^{2} + . .. + n^{2} = \frac{n (n + 1) (2 n + 1)}{6}$

Suy ra $I = \lim \frac{\sqrt{2 \frac{n (n + 1)}{2}} + n}{\sqrt[3]{48 (\frac{n (n + 1) (2 n + 1)}{6})} + 2 n}$ $= \lim \frac{\sqrt{n^{2} (1 + \frac{1}{n})} + n}{\sqrt[3]{8 n^{3} (1 + \frac{1}{n}) (2 + \frac{1}{n})} + 2 n}$

$= \lim \frac{n (\sqrt{(1 + \frac{1}{n})} + 1)}{n (\sqrt[3]{8 (1 + \frac{1}{n}) (2 + \frac{1}{n})} + 2)}$ $= \frac{\sqrt{1} + 1}{\sqrt[3]{8} + 2} = \frac{1}{2}$

Câu 37:

Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Tính góc giữa hai đường thẳng MN và AP.

Xem đáp án

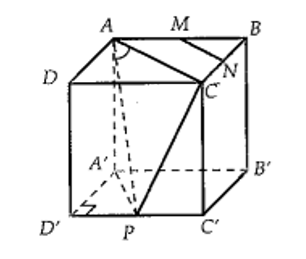
Giả sử hình lập phương có cạnh bằng a và MN // AC nên: $(\hat{MN, AP}) = (\hat{AC, AP})$

Vì ${ΔA}^{'} D^{'} P$ vuông tại D' nên $A^{'} P = \sqrt{A^{'} {D^{'}}^{2} + D^{'} P^{2}}$ $= \sqrt{a^{2} + {(\frac{a}{2})}^{2}}$ $= \frac{a \sqrt{5}}{2}$

${ΔAA}^{'} P$ vuông tại A' nên $AP = \sqrt{A^{'} A^{2} + A^{'} P^{2}}$ $= \sqrt{a^{2} + {(\frac{a \sqrt{5}}{2})}^{2}}$ $= \frac{3 a}{2}$

${ΔCC}^{'} P$ vuông tại C' nên $CP = \sqrt{C {C^{'}}^{2} + C^{'} P^{2}}$ $= \sqrt{a^{2} + \frac{a^{2}}{4}}$ $= \frac{a \sqrt{5}}{2} .$

Ta có AC là đường chéo của hình vuông ABCD nên $AC = a \sqrt{2}$

Áp dụng định lý cosin trong tam giác ACP ta có:

${CP}^{2} = {AC}^{2} + {AP}^{2} - 2 AC . AP . \cos \hat{CAP}$

$\begin{array}{l} \Rightarrow \cos \hat{CAP} = \frac{1}{\sqrt{2}} \\ \Rightarrow \hat{CAP} = 45 ° < 90 ° \end{array}$

Vậy $(\hat{AC; AP}) = \hat{CAP} = 45 °$ hay $(\hat{MN; AP}) = 45 °$

Câu 38:

Tính giới hạn sau:

\lim_{x \to 1} \frac{\sqrt{2 x^{2} + 7} - 3 \sqrt[3]{3 x + 5} + \sqrt[4]{3 x + 78}}{x^{2} - 1}

Xem đáp án

$\lim_{x \to 1} (\frac{\sqrt{2 x^{2} + 7} - 3 \sqrt[3]{3 x + 5} + \sqrt[4]{3 x + 78}}{x^{2} - 1})$

$= \lim_{x \to 1} (\frac{\sqrt{2 x^{2} + 7} - 3}{x^{2} - 1} - 3 \frac{\sqrt[3]{3 x + 5} - 2}{x^{2} - 1}$ $+ \frac{\sqrt[4]{3 x + 78} - 3}{x^{2} - 1})$

$= \lim_{x \to 1} \frac{1}{x^{2} - 1} (\frac{2 x^{2} - 2}{\sqrt{2 x^{2} + 7} + 3}$ $- 3 \frac{3 x - 3}{\sqrt[3]{{(3 x + 5)}^{2}} + 2 \sqrt[3]{3 x + 5} + 4}$ $+ \frac{3 x - 3}{(\sqrt[4]{3 x + 78} + 3) (\sqrt{3 x + 78} + 9)})$

$= \lim_{x \to 1} (\frac{2}{\sqrt{2 x^{2} + 7} + 3}$ $- \frac{9}{(\sqrt[3]{{(3 x + 5)}^{2}} + 2 \sqrt[3]{3 x + 5} + 4) (x + 1)}$ $+ \frac{3}{(x + 1) (\sqrt[4]{3 x + 78} + 3) (\sqrt{3 x + 78} + 9)})$

$= \frac{- 1}{36} .$

Câu 39:

Cho hàm số

f (x) = \{\begin{cases} \sin x khi cosx \geq 0 \\ 1 + \cos x khi cosx < 0 \end{cases}

. Chỉ ra các điểm gián đoạn của hàm số trên khoảng (0; 2021)?

Xem đáp án

Xét hàm số f(x) trên đoạn $[0; 2 π]$ , khi đó:

$f (x) = \{\begin{cases} sinx khi x \in [0; \frac{π}{2}] \cup [\frac{3 π}{2}; 2 π] \\ 1 + cosx khi x \in (\frac{π}{2}; \frac{3 π}{2}) \end{cases}$

Ta có $\lim_{x \to 0^{+}} f (x) = 0 = f (0)$ ; $\lim_{x \to 2 π^{-}} f (x) = 0 = f (2 π)$ .

Hàm số rõ ràng liên tục trên các khoảng $[0; \frac{π}{2})$ ; $(\frac{π}{2}; \frac{3 π}{2})$ và $(\frac{3 π}{2}; 2 π]$ .

Ta xét tại $x = \frac{π}{2}$ :

$\lim_{x \to {(\frac{π}{2})}^{+}} f (x) = \lim_{x \to {(\frac{π}{2})}^{+}} (1 + cosx) = 1$ ; $\lim_{x \to {(\frac{π}{2})}^{+}} f (x) = \lim_{x \to {(\frac{π}{2})}^{+}} (1 + cosx) = 1$ ; $f (\frac{π}{2}) = 1$

Như vậy $\lim_{x \to {(\frac{π}{2})}^{-}} f (x) = \lim_{x \to {(\frac{π}{2})}^{+}} f (x)$ $= f (\frac{π}{2})$ nên hàm số f(x) liên tục tại điểm $x = \frac{π}{2}$

Ta xét tại $x = \frac{3 π}{2}$ :

$\lim_{x \to {(\frac{3 π}{2})}^{+}} f (x) = \lim_{x \to {(\frac{3 π}{2})}^{+}} \sin x = - 1$ ; $\lim_{x \to {(\frac{3 π}{2})}^{-}} f (x) = \lim_{x \to {(\frac{3 π}{2})}^{-}} (1 + \cos x) = 1$ ;

Vì $\lim_{x \to {(\frac{3 π}{2})}^{-}} f (x) \neq \lim_{x \to {(\frac{3 π}{2})}^{+}} f (x)$ nên hàm số f(x) gián đoạn tại điểm $x = \frac{3 π}{2}$

Do đó, trên đoạn $[0; 2 π]$ hàm số chỉ gián đoạn tại điểm $x = \frac{3 π}{2}$

Do tính chất tuần hoàn của hàm số y = cosx và y = sinx suy ra hàm số gián đoạn tại các điểm $x = \frac{3 π}{2} + k 2 π$ $, k \in ℤ$

Ta có $x \in (0; 2021)$ $\Leftrightarrow 0 < \frac{3 π}{2} + k 2 π < 2021$ $\Leftrightarrow - \frac{3}{4} < k < \frac{2021}{2 π} - \frac{3}{4} \approx 320 .902$

Vì $k \in ℤ$ nên $k \in \{0,1,2,....,320\}$

Vậy, hàm số f gián đoạn tại các điểm $x = \frac{3 π}{2} + k 2 π$ với $k \in \{0,1,2,....,320\}$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 5)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương