Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 20)
-
3934 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 2:
Lời giải
Theo tính chất mối liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng thì đáp án A,C,Dđúng.
Trong đáp án B nếu a,b nằm trong mặt phẳng song song với (P) thì . Vậy kết luận ở câu B sai.
Câu 3:
Lời giải
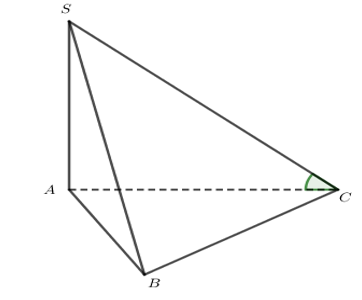
Ta có (1)
Hơn nữa, theo giả thiết nên A là hình chiếu của C lên mặt phẳng (ABC0 (2)
Từ (1) và (2) suy ra AC là hình chiếu vuông góc của SC lên mặt phẳng (ABC).
Khi đó góc giữa SC và mặt phẳng (ABC) là góc giữa SC và AC hay góc .
Tính góc
Ta có mà nên .
Mặt khác, ( theo giả thiết).
Suy ra tam giác SAC vuông cân tại A, suy ra .
Câu 4:
Trong các giới hạn sau giới hạn nào bằng 0 ?
Lời giải
Xét đáp án A, .
Xét đáp án B, vì .
Xét đáp án C, .
Xét đáp án D, .
Câu 5:
Cho tứ diện đều ABCD cạnh a. Tính tích vô hướng theo ![]() .
.
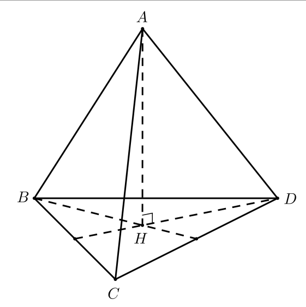
Tứ diện ABCD là tứ diện đều cạnh a nên suy ra tam giác ABC đều cạnh a.
Do đó
Câu 6:
Lời giải
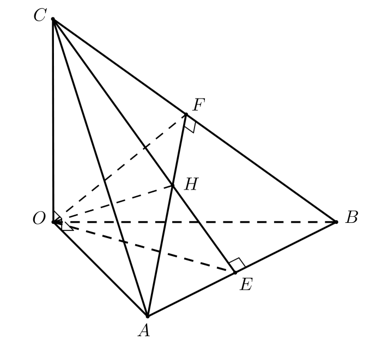
Kẻ , , .
Tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau do đó
.
Ta có Do đó đáp án A đúng.
Ta có Do đó đáp án C đúng.
Ta có
Do đó Do đó đáp án B đúng.
Ta có vuông tại O.
Suy ra OH không vuông góc với OA. Do đó đáp án D sai.
Câu 7:
Cho hàm số . Mệnh đề nào sau đây đúng ?
Lời giải
TXĐ :
Nên hàm số sẽ gián đoạn tại x=2
Câu 10:
Biết ba số theo thứ tự lập thành cấp số nhân. Giá trị của x bằng
Lời giải
Theo tính chất cấp số nhân ta có:
Câu 14:
Hàm số nào sau đây không liên tục tại x=2?
Lời giải
Hàm số có tập xác định nên không liên tục tại x=2.
Câu 19:
Hàm số liên tục trên
Lời giải
Đkxđ: . TXĐ: .
+ Lấy bất kì thuộc khoảng thì hàm số liên tục trên khoảng .
+ .
+ .
Vậy hàm số liên tục trên đoạn .
Câu 22:
Câu 23:
Dãy số nào sau đây không phải là cấp số nhân?
Lời giải
Xét đáp án A là cấp số nhân với
Xét đáp án B có , suy ra không phải cấp số nhân.
Xét đáp án C là cấp số nhân với .
Xét đáp án D là cấp số nhân với .
Câu 24:
Trong không gian cho ba đường thẳng phân biệt a,b,c Khẳng định nào sau đây đúng?
Lời giải
Đáp án B: chỉ đúng trong mặt phẳng.
Đáp án C: a và b có thể chéo nhau.
Đáp án D: đúng.
Câu 26:
Cho các hàm số Có bao nhiêu hàm số trong các hàm số đã cho liên tục trên ![]() ?
?
Lời giải
Vì các hàm số có tập xác định trên R nên chúng liên tục trên R
Hàm số liên tục trên từng khoảng xác định .
Vậy có 3 hàm số đã cho liên tục trên R.
Câu 27:
Chọn mệnh đề sai.
Lời giải
Ta có
+ Đáp án A đúng.
+ Đáp B đúng.
+
Đáp án C đúng.
Vậy đáp án D sai.
Câu 28:
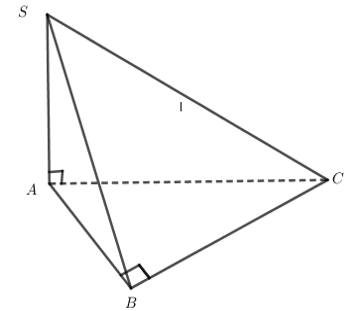
Ta có vuông tại A ( Do )
vuông tại A ( Do )
vuông tại B ( Do ).
Lại có mà suy ra nên vuông tại B.
Vậy Hình chóp SABC có 4 mặt là tam giác vuông.
Câu 30:
Cho hình lập phương . Góc giữa hai đường thẳng AD và DA' bằng
Lời giải
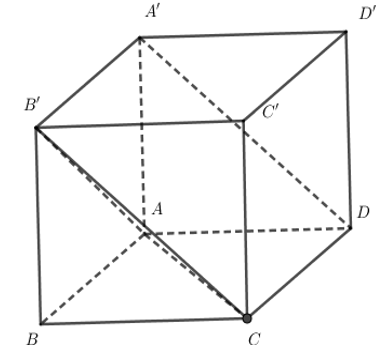
Ta có suy ra góc giữa hai đường thẳng AC và DA' là
Ta thấy lần lượt là đường chéo của các hình vuông , , nên tam giác đều. Suy ra .
Vậy .
Câu 31:
Cho hình chóp SABC có đáy là tam giác đều ABC cạnh a và . Gọi M là trung điểm của AB và là góc tạo bởi đường thẳng SM và mặt phẳng (ABC). Biết SC=a, tính .
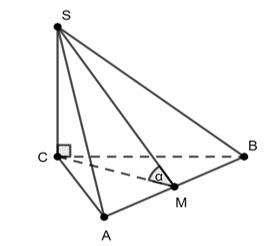
Ta có nên C là hình chiếu vuông góc của S xuống mặt phẳng (ABC).
Khi đó, CM là hình chiếu vuông góc của SM xuống mặt phẳng (ABC).
Do đó góc tạo bởi đường thẳng SM và mặt phẳng (ABC) là .
Tam giác SMC vuông tại C nên và .
Câu 32:
Cho hình chóp SABCD có đáy là hình vuông ABCD, và . Gọi E, F lần lượt là trung điểm của BC, SC. Góc giữa EF và mặt phẳng (SAD) bằng
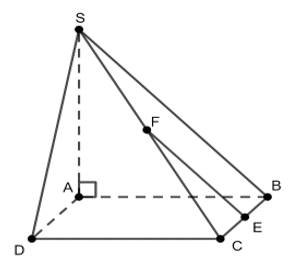
Ta có EF là đường trung bình trong nên . Khi đó góc giữa EF và mặt phẳng (SAD) là góc giữa SB và mặt phẳng (SAD).
Mặt khác, do , nên . Do đó A là hình chiếu vuông góc của B lên (SAD).
Suy ra, SA là hình chiếu vuông góc của SB lên (SAD).
Khi đó góc giữa SB và mặt phẳng (SAD) là .
Do vuông cân tại A nên .
Câu 33:
Có bao nhiêu giá trị nguyên của tham số thực m để I>12 biết .
Lời giải
Ta có
Do đó, .
. Do đó, có tất cả 5 giá trị m thoả mãn yêu cầu đề bài.
Câu 34:
Cho phương trình Khẳng định nào sau đây đúng?
Lời giải
Đặt , hàm số liên tục trên R. Ta có
phương trình có ít nhất 1 nghiệm thuộc (-1,0)
phương trình f(x)=0 có ít nhất 1 nghiệm thuộc (1,2)
phương trình f(x) có ít nhất 1 nghiệm thuộc (2,3)
Do nên ta sẽ có 3 nghiệm trên phân biệt và là phương trình bậc ba nên sẽ có tối đa 3 nghiệm. Vậy phương trình đã cho có đúng 3 nghiệm phân biệt.
Câu 35:
Cho hình chóp SABC có Gọi I là hình chiếu vuông góc của S lên mặt phẳng (ABC) Chọn khẳng định đúng trong các khẳng định sau.
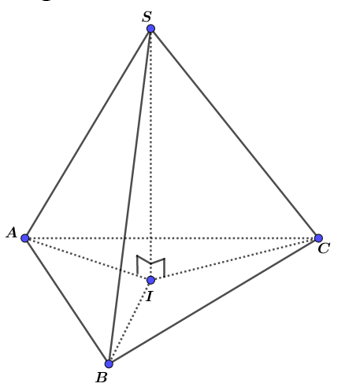
Ta có là các tam giác vuông tại I vì .
Xét vuông tại I và vuông tại I có: SI là cạnh chung, cạnh huyền SA=SB (cạnh huyền – cạnh góc vuông) (1).
Tương tự ta có (2).
Từ (1), (2) ta có . Vậy I là tâm đường tròn ngoại tiếp của .
Câu 36:
Biết tổng ( với là phân số tối giản). Tính tích a.b
Lời giải
Đặt
Ta có là tổng cấp số nhân lùi vô hạn với và công bội
Nên từ đó ta có .
Câu 38:
Cho cấp số nhân có và . Tính tổng 1000 số hạng đầu tiên của cấp số nhân đã cho.
Lời giải
Ta có . Và .
.
Câu 39:

Gọi N là trung điểm AC.
Ta có ABCD là hình chóp đều.
.
Ta có
.
Câu 40:
Hàm số đã cho xác định trên tập Với mọi ta có
Do đó hàm số liên tục trên khoảng
Câu 41:
Số điểm gián đoạn của hàm số ?
Lời giải
Hàm số đã cho xác định trên tập hợp .
Do đó f(x) gián đoạn tại 3 điểm là 1; và .
Câu 42:
Cho tứ diện ABCD có AC= 6a, BD=8a. Gọi M,N lần lượt là trung điểm của AD, BC Biết Tính độ dài đoạn thẳng MN
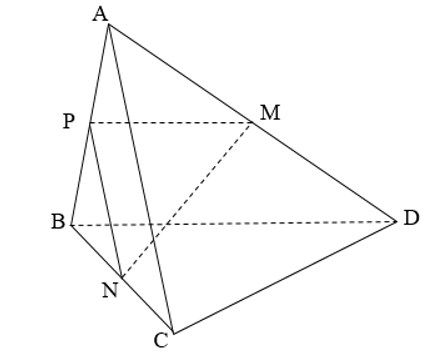
Gọi P là trung điểm của đoạn AB. Theo tính chất đường trung bình trong các tam giác ABD ta có PM song song với BD và
Tương tự, trong tam giác ABC ta có PN song song với AC và .
Theo giả thiết nên .
Trong tam giác vuông MPN, ta có .
Câu 44:
Cho hàm số f(x) xác định trên R và thỏa mãn thì bằng bao nhiêu?
Lời giải
Ta có .
Vậy .
Câu 45:
Gọi S là tập các giá trị của tham số thực m để hàm số liên tục tại x=1 Tích các phần tử của tập S bằng.
Lời giải
Tập xác định của hàm số: D=R.
Ta có: .
Mặt khác,
Khi đó, để hàm số liện tục lại thì
Hay
Vậy tích các phần tử của tập S bằng -6.
Câu 46:
Cho hình vuông ABCD có cạnh bằng a Người ta dựng hình vuông có cạnh bằng đường chéo của hình vuông ABCD; dựng hình vuông có cạnh bằng đường chéo của hình vuông và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích S của tất cả các hình vuông bằng 8 thì a bằng:
Lời giải
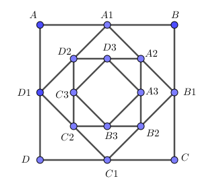
- Diện tích của hình vuông ABCD là .
- Diện tích của hình vuông là .
- Tương tự diện tích lần lượt là …..
Các diện tích này lập thành một CSN lùi vô hạn có và công bội và
Khi đó .
.
Câu 48:
Cho tứ diện ABCD có , các cạnh còn lại bằng nhau và bằng 4 Mặt phẳng (P) chứa cạnh AB và vuông góc với cạnh CD tại I Diện tích tam giác IAB lớn nhất bằng:
- Các và đều vì có các cạnh đều bằng 4.
- Gọi I là trung điểm của CD thì , . Mặt phẳng (P) chính là mặt phẳng (ABI).
- Mặt khác ta có AI và BI là các đường cao trong tam giác đều cạnh bằng 4 nên .
- Gọi H là trung điểm của AB thì IH là đường cao trong tam giác cân ABI
.
= .
Sử dụng bất đẳng thức Côsi ta có : .
Dấu bằng xảy ra khi .
Vậy diện tích tam giác IAB lớn nhất bằng 6.
Câu 49:
Cho hàm số f(x) xác định trên R thỏa mãn . Giới hạn bằng
Lời giải
Vì nên do nếu giới hạn này khác 0 thì giới hạn sẽ bằng vô cùng. Ta suy ra được .
Biến đổi
Do nên suy ra .
Vậy
Câu 50:
Cho hàm số . Biết a là giá trị để hàm số liên tục tại điểm . Tìm số nghiệm nguyên của bất phương trình
Lời giải
Hàm số liên tục tại điểm . Ta biến đổi
+) Nếu thì giới hạn (1) không tồn tại, hàm số không liên tục tại điểm 0 nên loại trường hợp này.
+) Nếu giới hạn (1) bằng . Vậy để hàm số liên tục tại điểm 0 khi và chỉ khi . Như vậy ta cần tìm số nghiệm nguyên của bất phương trình Giải ra ta được . Vậy bất phương trình có 4 nghiệm nguyên là .
