Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 12)
-
3946 lượt thi
-
5 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 4:
Cho hình chóp S.ABC có đáy ABC là tam vuông cân tại A, AB = Cạnh bên SA vuông góc với mặt phẳng (ABC) và
Gọi M là trung
điểm của cạnh BC.
a) Chứng minh đường thẳng BC vuông góc với mặt phẳng (SAM)
b) Xác định và tính góc giữa đường thẳng SC và mặt phẳng (ABC)
c) Gọi điểm I là hình chiếu vuông góc của điểm A lên cạnh SC và H là giao điểm
của BI và SM. Chứng minh H là trực tâm của tam giác SBC.
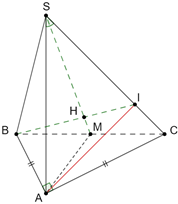
a) Ta có: SA ^ (ABC) suy ra SA ^ BC.
Tam giác ABC vuông cân tại A với M là trung điểm của BC nên suy ra AM ^ BC
Do đó BC ^ (SAM).
b) Ta có CA ^ AB và do SA ^ (ABC) nên SA ^ AC.
Do đó AC ^ (SAB).
Vậy góc giữa đường thẳng SC và mặt phẳng (ABC) là góc .
Ta có:
Do đó .
c) Ta có
+) BC ^ (SAM) Þ BC ^ SM (1)
+) BA ^ SA và BA ^ AC nên suy ra BA ^ (SAC) Þ BA ^ SC
Lại có AI ^ SC.
Nên suy ra SC ^ (BAI) Þ SC ^ BI (2)
Từ (1) và (2), xét trong tam giác SBC nên H là trực tâm của tam giác SBC.
Câu 5:
Chứng minh rằng phương trình a.cos4 x + b.cos3 x - 2c.cos x = 2a.sin3 x luôn có nghiệm với mọi tham số a, b, c.
Ta có a.cos4 x + b.cos3 x - 2c.cos x = 2a.sin3 x.
Xét hàm số f (x) = a.cos4 x + b.cos3 x - 2c.cos x - 2a.sin3 x.
+) Với a = 0 Þ f (x) = b.cos3 x - 2c.cos x = cos x.( b.cos2 x - 2c) = 0
Nên luôn cho nghiệm cos x = 0 (*)
+) Với a ¹ 0 Þ f (x) = a.cos4 x + b.cos3 x - 2c.cos x - 2a.sin3 x
f (x) liên tục trên ℝ nên liên tục trên đoạn (1)
Ta có:
(2)
Từ (1) và (2) nên suy ra phương trình f (x) = 0 có ít nhất một nghiệm thuộc khoảng (**)
Từ (*) và (**), vậy suy ra phương trình a.cos4 x + b.cos3 x - 2c.cos x = 2a.sin3 x luôn có nghiệm với mọi tham số a, b, c.