39 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 16)

Câu 1:

Dãy số nào sau đây có giới hạn bằng 0 ?

A. $\frac{n^{2} + 1}{2 n + 3}$

B. $n - 2 n^{2}$

C. $\frac{n + 1}{2 n + 1}$

D. $\frac{1}{2 n + 1}$

Xem đáp án

Ta có $\lim \frac{1}{2 n + 1} = \lim \frac{\frac{1}{n}}{2 + \frac{1}{n}} = \frac{0}{2} = 0$

Câu 2:

Dãy số nào sau đây có giới hạn khác 0 ?

A. $\frac{2 n + 1}{n + 5}$

B. $\frac{1}{n + 1}$

C. ${(\frac{3}{4})}^{n}$

D. $\frac{2 n + 1}{n^{2} + 1}$

Xem đáp án

Ta có $\lim \frac{2 n + 1}{n + 5} = \lim \frac{2 + \frac{1}{n}}{1 + \frac{5}{n}} = \frac{2}{1} = 2$

Câu 3:

$\lim \frac{2 n - 1}{n^{3} + 5}$ bằng

A. 0

B. $- \infty$

C. $+ \infty$

D. 2

Xem đáp án

Ta có $\lim \frac{2 n - 1}{n^{3} + 5} = \lim \frac{\frac{2}{n^{2}} - \frac{1}{n^{3}}}{1 + \frac{5}{n^{3}}} = \frac{0}{1} = 0$

Câu 4:

$\lim \frac{1 + 5^{n}}{4^{n} - 5^{n + 1}}$ bằng

A. $+ \infty$

B. $- \infty$

C. 0

D. $\frac{- 1}{5}$

Xem đáp án

Ta có $\lim \frac{1 + 5^{n}}{4^{n} - 5^{n + 1}} = \lim \frac{{(\frac{1}{5})}^{n} + 1}{{(\frac{4}{5})}^{n} - 5} = \frac{1}{- 5} = - \frac{1}{5}$

Câu 5:

Cho dãy số

(u_{n})

thỏa mãn

\lim (u_{n} - 3) = 0

. Tìm

\lim u_{n} = 0

A. $\lim u_{n} = 2$

B. $\lim u_{n} = - 3$

C. $\lim u_{n} = 0$

D. $\lim u_{n} = 3$

Xem đáp án

Theo định nghĩa giới hạn hữu hạn của dãy số ta có $\lim (u_{n} - 3) = 0 \Rightarrow \lim u_{n} = 3$

Câu 6:

Dãy số nào có giới hạn khác 0

A. $u_{n} = \frac{1}{n}$

B. $u_{n} = \frac{1}{n^{2}}$

C. $u_{n} = 1 - \frac{1}{n}$

D. $u_{n} = {(\frac{1}{2})}^{n}$

Xem đáp án

Lời giải

$\lim \frac{1}{n} = \lim \frac{1}{n^{2}} = \lim {(\frac{1}{2})}^{n} = 0$ .

$\lim (1 - \frac{1}{n}) = 1 \neq 0$ .

Câu 7:

Cho cấp số nhân lùi vô hạn có số hạng tổng quát $u_{n} = {(\frac{1}{2})}^{n}$ . Tính tổng của cấp số nhân đó

A. 1

B. $\frac{1}{2}$

C. 2

D. $\frac{1}{4}$

Xem đáp án

Lời giải

Gọi công bội của cấp số nhân q là

$u_{n} = {(\frac{1}{2})}^{n} \Rightarrow u_{1} = \frac{1}{2}; u_{2} = \frac{1}{4} \Rightarrow q = \frac{1}{2}$

Tính tổng của cấp số nhân là $S = \frac{u_{1}}{1 - q} = 1$

Câu 8:

Có bao nhiêugiá trị của a để giới hạn

\lim_{x \to a} (x^{2} + 3 x + 2) = 0

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Lời giải

$\lim_{x \to a} (x^{2} + 3 x + 2) = 0 \Leftrightarrow a^{2} + 3 a + 2 = 0 \Leftrightarrow [\begin{array}{l} a = - 1 \\ a = - 2 \end{array}$ .

Vậy có hai giá trị của a.

Câu 9:

Tính

I = \lim_{x \to 0} (x^{2} - x + 3)

A. 0

B. 3

C. 6

D. -5

Xem đáp án

Lời giải

Ta có

I = \lim_{x \to 0} (x^{2} - x + 3) = 0^{2} - 0 + 3 = 3

Câu 10:

$\lim_{x \to - \infty} (x^{3} + x + 3)$ bằng

A. 3

B. $+ \infty$

C. $- \infty$

D. -3

Xem đáp án

Lời giải

Ta có $\lim_{x \to - \infty} (x^{3} + x + 3) = \lim_{x \to - \infty} x^{3} (1 + \frac{1}{x^{2}} + \frac{3}{x^{3}}) = - \infty$ .

(Vì $\lim_{x \to - \infty} x^{3} = - \infty$ và $\lim_{x \to - \infty} (1 + \frac{1}{x^{2}} + \frac{3}{x^{3}}) = 1 > 0$ ).

Câu 11:

Tính $N = \lim_{x \to + \infty} \frac{6 x + 2}{x + 1}$ .

A. 6

B. 2

C. 1

D. -1

Xem đáp án

Lời giải

Ta có $N = \lim_{x \to + \infty} \frac{6 x + 2}{x + 1} = \lim_{x \to + \infty} \frac{6 + \frac{2}{x}}{1 + \frac{1}{x}} = 6$

Câu 12:

$\lim_{x \to 3^{-}} \frac{3 x + 2}{x - 3}$ bằng

A. $- \infty$

B. $+ \infty$

C. 2

D. -3

Xem đáp án

Lời giải

Ta có

\lim_{x \to 3^{-}} \frac{3 x + 2}{x - 3} = - \infty

(vì

\lim_{x \to 3^{-}} (3 x + 2) = 3.3 + 2 = 11 > 0

và

\lim_{x \to 3^{-}} (x - 3) = 0

;

x - 3 < 0

).

Câu 13:

Nếu $\lim_{x \to 0} f (x) = 5$ thì $\lim_{x \to 0} [3 x - 4 f (x)]$ bằng bao nhiêu?

A. -17

B. -1

C.1

D. -20

Xem đáp án

Lời giải

Ta có: $\lim_{x \to 0} f (x) = 5$ nên $\lim_{x \to 0} [3 x - 4 f (x)] = \lim_{x \to 0} (3 x) - 4 \lim_{x \to 0} f (x)$ $= 3.0 - 4.5 = - 20$ .

Câu 14:

Cho các hàm số $y = \cos x (I)$ , $y = \sin \sqrt{x} (I I)$ và $y = \tan x (I I I)$ . Hàm số nào liên tục trên R ?

A. $(I), (I I)$

B. (I)

C. $(I), (I I), (I I I)$

D. (III)

Xem đáp án

Lời giải

Ta có: Hàm số $y = \cos x$ có tập xác định là R nên liên tục trên R.

Hàm số $y = \sin \sqrt{x}$ có tập xác định là $[0; + \infty)$ nên không liên tục trên R .

Hàm số $y = \tan x$ có tập xác định là $ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ nên không liên tục trên R .

Câu 15:

Tìm m để hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 1}{x - 1} k h i x \neq 1 \\ m + 2 k h i x = 1 \end{cases}$ liên tục tại điểm $x_{0} = 1$ .

A. m=3

B. m=0

C. m=4

D. m=1

Xem đáp án

Lời giải

TXĐ: $D = ℝ \Rightarrow x_{0} = 1 \in D$ .

Ta có : $f (1) = m + 2$ .

$\lim_{x \to 1} \frac{x^{2} - 1}{x - 1} = \lim_{x \to 1} \frac{(x + 1) (x - 1)}{x - 1} = \lim_{x \to 1} (x + 1) = 2$ .

Hàm số $f (x)$ liên tục tại điểm $x_{0} = 1$ khi và chỉ khi $\lim_{x \to 1} f (x) = f (1) \Rightarrow m + 2 = 2 \Leftrightarrow m = 0$ .

Câu 16:

Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?

A. Hình thang.

B. Hình bình hành.

C. Hình chữ nhật.

D. Hình thoi.

Xem đáp án

Lời giải

Do phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau, nên không thể có đáp án A.

Câu 17:

Cho hình hộp $A B C D . A^{'} B^{'} C^{'} D^{'}$ . Các vectơ nào sau đây đồng phẳng?

A. $\vec{A B}$ , $\vec{A D}$ , $\vec{A A^{'}}$

B. $\vec{B A}$ , $\vec{B C}$ , $\vec{B^{'} D^{'}}$

C. $\vec{B C}$ , $\vec{B B^{'}}$ , $\vec{B D^{'}}$

D. $\vec{D A}$ , $\vec{A^{'} D}$ , $\vec{A^{'} C}$

Xem đáp án

Lời giải

Ta có $\vec{B A}$ , $\vec{B C}$ chứa trong $m p (A B C D)$ và $\vec{B^{'} D^{'}}$ song song với $m p (A B C D)$ nên các vectơ $\vec{B A}$ , $\vec{B C}$ và $\vec{B^{'} D^{'}}$ đồng phẳng.

Câu 18:

Cho tứ diện ABCD có I, J lần lượt là trung điểm của AB và CD. Đẳng thức nào sau đây là đúng?

A. $\vec{I J} = \frac{1}{2} (\vec{A D} + \vec{C B})$

B. $\vec{I J} = \frac{1}{2} (\vec{A C} + \vec{D B})$

C. $\vec{I J} = \frac{1}{2} (\vec{A D} + \vec{B C})$

D. $\vec{I J} = \frac{1}{2} (\vec{C A} + \vec{D B})$

Xem đáp án

Lời giải

Ta có: $\vec{I J} = \vec{I A} + \vec{A D} + \vec{D J}$ .

$\vec{I J} = \vec{I B} + \vec{B C} + \vec{C J}$ .

Suy ra: $2 \vec{I J} = (\vec{I A} + \vec{I B}) + \vec{A D} + \vec{B C} + (\vec{D J} + \vec{J C}) = \vec{0} + \vec{A D} + \vec{B C} + \vec{0} = \vec{A D} + \vec{B C}$ .

Vậy: $\vec{I J} = \frac{1}{2} (\vec{A D} + \vec{B C})$ .

Câu 19:

Trong không gian cho 3 đường thẳng a,b,c. Khẳng định nào sau đây là đúng?

A. Nếu $a ⊥ b$ và $a ⊥ c$ thì $a / / c$ .

B. Nếu $a / / b$ và $c ⊥ a$ thì

c ⊥ b

.

C. Nếu

a ⊥ c

và

b ⊥ c

thì

a ⊥ b

.

D. Nếu

a ⊥ b

và

b ⊥ c

thì

a ⊥ c

.

Xem đáp án

Lời giải

Cho 2 đường thẳng song song, nếu 1 đường thẳng thứ 3 vuông góc với 1 trong 2 đường thẳng đó thì cũng vuông góc với đường thẳng còn lại.

Vậy: Nếu $a / / b$ và $c ⊥ a$ thì $c ⊥ b$ là khẳng định đúng.

Câu 20:

Trong không gian cho 2 vectơ $\vec{a}$ và $\vec{b}$ . Khẳng định nào sau đây là đúng?

A. $\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = 0$

B. $\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = \vec{0}$

C. $\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} = \vec{b}$

D. $\vec{a} ⊥ \vec{b} \Leftrightarrow (\vec{a}, \vec{b}) = 90^{0}$

Xem đáp án

Lời giải

Phương án A sai nếu $\vec{a} = \vec{0}$ hoặc $\vec{b} = \vec{0}$ .

Phương án B sai vì tích của 2 vec tơ là 1 số.

Phương án C sai.

Theo định nghĩa, 2 đường thẳng vuông góc với nhau nếu góc giữa chúng bằng $90 °$ nên D đúng.

Câu 21:

Cho dãy số

(u_{n})

với

u_{n} = \frac{2 n + \sqrt{n^{2} + 5}}{n {.4}^{n}}

. Tính

\lim u_{n}

.

A. 4

B. 2

C. 1

D. 0

Xem đáp án

Lời giải

Ta có: $u_{n} = \frac{2 n + \sqrt{n^{2} + 5}}{n {.4}^{n}}$ = $\frac{\frac{2 n + \sqrt{n^{2} + 5}}{n}}{\frac{n {.4}^{n}}{n}}$ = $\frac{2 + \sqrt{1 + \frac{5}{n^{2}}}}{4^{n}}$ = $\frac{1}{4^{n}} (2 + \sqrt{1 + \frac{5}{n^{2}}})$ .

Vì $\lim \frac{5}{n^{2}} = 0$ nên $\lim (2 + \sqrt{1 + \frac{5}{n^{2}}}) = 3$ và $\lim \frac{1}{4^{n}} = 0$ . Do đó $\lim u_{n} = 0$ .

Vậy $\lim u_{n} = 0$ .

Câu 22:

Cho dãy số $(u_{n})$ với $u_{n} = \frac{1 + 2 + 3 + ... + n}{1010 n^{2} + 1011}$ . Khi đó $\lim (u_{n} + 1)$ bằng

A. $\frac{2020}{2021}$

B . $\frac{2019}{2020}$

C. $\frac{2021}{2020}$

D. $\frac{2021}{2022}$

Xem đáp án

Lời giải

Ta có: $u_{n} = \frac{1 + 2 + 3 + ... + n}{1010 n^{2} + 1011}$ = $u_{n} = \frac{1 + 2 + 3 + ... + n}{1010 n^{2} + 1011}$ = $\frac{n^{2} + n}{2020 n^{2} + 2022}$ .

Do đó

$\lim (u_{n} + 1)$ = $\lim (\frac{n^{2} + n}{2020 n^{2} + 2022} + 1)$

= $\lim (\frac{1 + \frac{1}{n}}{2020 + \frac{2022}{n^{2}}} + 1)$ = $\frac{1}{2020} + 1$ = $\frac{2021}{2020}$ .

Vậy $\lim (u_{n} + 1) = \frac{2021}{2020}$ .

Câu 23:

Trong các giới hạn sau, giới hạn nào bằng 0?

A. $\lim \frac{3 n^{2} + n}{n^{2} + 7}$

B. $\lim \frac{2 - n^{3} + n^{2}}{n^{2} - 4}$

C. $\lim \frac{4 n - 5 n^{2}}{n^{2} - 4}$

D. $\lim \frac{2 n + 4 n^{2}}{3 n^{3} + 5}$

Xem đáp án

Lời giải

Ta có:

+) $\lim \frac{3 n^{2} + n}{n^{2} + 7}$ = $\lim \frac{3 + \frac{1}{n}}{1 + \frac{7}{n^{2}}}$ = 3.

+) $\lim \frac{2 - n^{3} + n^{2}}{n^{2} - 4}$ = $\lim \frac{\frac{2}{n^{3}} - 1 + \frac{1}{n}}{\frac{1}{n} - \frac{4}{n^{3}}}$ = $- \infty$ .

+) $\lim \frac{4 n - 5 n^{2}}{n^{2} - 4}$ = $\lim \frac{\frac{4}{n} - 5}{1 - \frac{4}{n^{2}}}$ = -5.

+) $\lim \frac{2 n + 4 n^{2}}{3 n^{3} + 5}$ = $\lim \frac{\frac{2}{n^{2}} + \frac{4}{n}}{3 + \frac{5}{n^{3}}}$ = 0.

Vậy $\lim \frac{2 n + 4 n^{2}}{3 n^{3} + 5} = 0$

Câu 24:

$\lim_{x \to - 3} \frac{x^{2} + 2 x - 3}{x + 3}$ bằng

A. 4

B. 0

C. -2

D. -4

Xem đáp án

Ta có $\lim_{x \to - 3} \frac{x^{2} + 2 x - 3}{x + 3} = \lim_{x \to - 3} \frac{(x - 1) (x + 3)}{x + 3} = \lim_{x \to - 3} (x - 1) = - 4$

Câu 25:

Cho hàm số

f (x) = \sqrt{2 x^{2} - 4 x + 5}

. Khẳng định nào dưới đây đúng?

A. $\lim_{x \to - \infty} f (x) = - \infty$

B. $\lim_{x \to - \infty} f (x) = + \infty$

C. $\lim_{x \to - \infty} f (x) = 2$

D. $\lim_{x \to - \infty} f (x) = - 2$

Xem đáp án

Lời giải

Hàm số $f (x) = \sqrt{2 x^{2} - 4 x + 5}$ xác định trên R .

$f (x) = \sqrt{2 x^{2} - 4 x + 5} = \sqrt{x^{2} (2 - \frac{4}{x} + \frac{5}{x^{2}})} = |x| \sqrt{2 - \frac{4}{x} + \frac{5}{x^{2}}}$ .

Vì

\lim_{x \to - \infty} |x| = + \infty

và

\lim_{x \to - \infty} \sqrt{2 - \frac{4}{x} + \frac{5}{x^{2}}} = 2 > 0

nên

\lim_{x \to - \infty} \sqrt{2 x^{2} - 4 x + 5} = + \infty

Câu 26:

$\lim_{x \to 2^{+}} \frac{x^{2} + x - 1}{x^{2} - 4}$ bằng

A. $- \infty$

B. 3

C. 0

D. $+ \infty$

Xem đáp án

Lời giải

Ta có: $\lim_{x \to 2^{+}} (x^{2} + x - 1) = 5 > 0$ .

$\lim_{x \to 2^{+}} (x^{2} - 4) = 0$ và $x^{2} - 4 > 0$ khi $x \to 2^{+}$ .

Suy ra $\lim_{x \to 2^{+}} \frac{x^{2} + x - 1}{x^{2} - 4} = + \infty$ .

Câu 27:

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{3} - 8}{x - 2} khi x \neq 2 \\ m x + 1 khi x = 2 \end{cases}$ . Tìm tất cả các giá trị của tham số thực m để hàm số liên tục tại x=2.

A. $m = \frac{17}{2}$

B. $m = \frac{15}{2}$

C. $m = \frac{13}{2}$

D. $m = \frac{11}{2}$

Xem đáp án

Lời giải

Ta có: Hàm số f(x) xác định trên R.

Ta có $f (2) = 2 m + 1$ và $\lim_{x \to 2} f (x) = \lim_{x \to 2} \frac{x^{3} - 8}{x - 2} = \lim_{x \to 2} (x^{2} + 2 x + 4) = 12$ .

(có thể dùng MTCT để tính giới hạn của hàm số)

Để f(x) liên tục tại x=2 thì $\lim_{x \to 2} f (x) = f (2)$ $\Leftrightarrow 2 m + 1 = 12 \Leftrightarrow m = \frac{11}{2}$ .

Câu 28:

Cho hàm số

f (x) = \{\begin{cases} \frac{x^{2} - 1}{x - 1} khi x \neq 1 \\ 2         khi x = 1 \end{cases} v

. Mệnh đề nào sau đây đúng ?

A. f(1) không tính được.

B. $\lim_{x \to 1} f (x) = 0$ .

C.f(x) gián đoạn tại x=1.

D. f(x) liên tục tại x=1.

Xem đáp án

Lời giải

Ta có: Hàm số f(x) xác định trên R

$\lim_{x \to 1} f (x) = \lim_{x \to 1} \frac{x^{2} - 1}{x - 1} = \lim_{x \to 1} (x + 1) = 2_{}$ và $f (1) = 2$ .

Suy ra hàm số đã cho liên tục tại x=1.

Câu 29:

Giá trị của tham số a để hàm số $f (x) = \{\begin{cases} \frac{\sqrt{x} - 1}{x - 1} khi x > 1 \\ a x - \frac{1}{2} khi x \leq 1 \end{cases}$ liên tục tại điểm x=1 là

A. -1

B. $\frac{- 1}{2}$

C. 1

D. $\frac{1}{2}$

Xem đáp án

Lời giải

Ta có: Hàm số f(x) có tập xác định $[0; + \infty)$

Ta có: $\lim_{x \to 1^{+}} f (x)$ $= \lim_{x \to 1^{+}} \frac{\sqrt{x} - 1}{x - 1}$ $= \lim_{x \to 1^{+}} \frac{\sqrt{x} - 1}{(\sqrt{x} - 1) (\sqrt{x} + 1)}$ $= \lim_{x \to 1^{+}} \frac{1}{\sqrt{x} + 1} = \frac{1}{2}$

$\lim_{x \to 1^{-}} f (x)$ $= \lim_{x \to 1^{-}} (a x - \frac{1}{2})$ $= a - \frac{1}{2}$ và $f (1) = a - \frac{1}{2}$

Hàm số liên tục điểm x=1

\Rightarrow

a - \frac{1}{2} = \frac{1}{2}

\Leftrightarrow

a =1 .

Câu 30:

Tìm m để hàm số

f (x) = \{\begin{matrix} \frac{\sqrt{x - 1} - 1}{x - 2} & khi & 1 \leq x \neq 2 \\ 1 - m & khi & x = 2 \end{matrix}

liên tục tại điểm x=2

A. $\frac{3}{2}$

B. 2

C. 1

D. $\frac{1}{2}$

Xem đáp án

Lời giải

Ta có:

$\lim_{x \to 2} \frac{\sqrt{x - 1} - 1}{x - 2} = \lim_{x \to 2} \frac{x - 2}{(x - 2) (\sqrt{x - 1} + 1)} = \lim_{x \to 2} \frac{1}{(\sqrt{x - 1} + 1)} = \frac{1}{2}$

Hàm số liên tục tại điểmx=2 khi và chỉ khi $\lim_{x \to 2} f (x) = f (2) \Leftrightarrow \frac{1}{2} = 1 - m \Leftrightarrow m = \frac{1}{2}$

Câu 31:

Cho tứ diện có tABCDrọng tâm G . Gọi I,J lần lượt là trung điểm của AD và BC . Khẳng định nào sau đây đúng ?

A. $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = 2 \vec{IJ}$

B. $\vec{G A} - \vec{G B} + \vec{G C} - \vec{G D} = \vec{0}$

C. $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{G I} - \vec{G J}$

D. $\vec{A B} + \vec{D C} = 2 \vec{IJ}$

Xem đáp án

Lời giải

Ta có: $\vec{A B} + \vec{D C} = (\vec{A I} + \vec{IJ} + \vec{J B}) + (\vec{D I} + \vec{IJ} + \vec{J C}) = (\vec{A I} + \vec{D I}) + (\vec{J B} + \vec{J C}) + 2 \vec{IJ} = \vec{0} + \vec{0} + 2 \vec{IJ} = 2 \vec{IJ}$

Câu 32:

Cho hình lập phương $A B C D . A^{'} B^{'} C^{'} D^{'}$ có cạnh 2a . Tích vô hướng $\vec{A C} . \vec{A D^{'}}$ bằng:

A. a

B. $2 a^{2}$

C. $4 a^{2}$

D. $4 a^{2}$

Xem đáp án

Ta có:

Tam giác $A C D^{'}$ là tam giác đều cạnh $2 \sqrt{2} a$ nên $\vec{A C} . \vec{A D^{'}} = 2 a \sqrt{2} .2 a \sqrt{2} . c os 60^{0} = 4 a^{2}$

Câu 33:

Cho hình lập phương ABCDA'B'C'D' cạnh a. Góc giữa hai đường thẳng AC và DA' bằng:

A. $30^{○}$

B. $90 °$

C. $45 °$

D. $60 °$

Xem đáp án

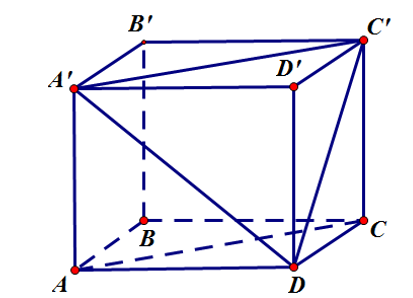
Cho hình lập phương ABCDA'B'C'D' cạnh a. Góc giữa hai đường thẳng AC và DA' bằng: (ảnh 1)

+ Có $A C ∥ A^{'} C^{'}$ nên $(\hat{A C; D A^{'}}) = (\hat{A^{'} C^{'}; D A^{'}}) = \hat{C^{'} A^{'} D} = 60^{○}$ (Vì tam giác $C^{'} A^{'} D$ là tam giác đều cạnh bằng $a \sqrt{2}$ ).

Câu 34:

Cho tứ diện ABCDcó $A C = 6; B D = 8$ . Gọi M,N lần lượt là trung điểm của AD, BC Biết $A C ⊥ B D .$ Tính độ dài đoạn thẳng MN

A. $M N = \sqrt{10}$

B. $M N = 7$

C. $M N = 10$

D. $M N = 5$

Xem đáp án

+ Gọi P là trung điểm của CD. Dễ thấy $M P ∥ A C$ và $N P ∥ B D$ ( Tính chất đường trung bình); mà $A C ⊥ B D$ $\Rightarrow M P ⊥ N P$ hay tam giác MNP vuông tại P.

+ Lại có $M P = \frac{1}{2} A C = 3; N P = \frac{1}{2} B D = 4$ $\Rightarrow M N = \sqrt{M P^{2} + N P^{2}} = \sqrt{3^{2} + 4^{2}} = 5$ .

Câu 35:

Cho tứ diện ABCD có $A B ⊥ A C; A B ⊥ B D$ . Gọi P,Q lần lượt là trung điểm của AB, CD. Chọn khẳng định đúng:

A. $A B ⊥ P Q$

B. $A B ⊥ C D$

C. $B D ⊥ A C$

D. $A C ⊥ P Q$

Xem đáp án

+ Có $\{\begin{cases} \vec{P Q} = \vec{P A} + \vec{A C} + \vec{C Q} \\ \vec{P Q} = \vec{P B} + \vec{B D} + \vec{D Q} \end{cases}$ $\Rightarrow \vec{P Q} = \frac{1}{2} (\vec{A C} + \vec{B D})$ .

+ Vậy $\vec{P Q} . \vec{A B} = \frac{1}{2} (\vec{A C} + \vec{B D}) . \vec{A B}$ $= \frac{1}{2} . (\vec{A B} . \vec{A C} + \vec{B D} . \vec{A B})$ $= 0 \Rightarrow A B ⊥ P Q$ .

(Vì $A B ⊥ A C; A B ⊥ B D$ ).

Câu 36:

Tính giới hạn sau:

\lim_{n \to \infty} \frac{1 + \frac{1}{2} + ... + \frac{1}{2^{n}}}{1 + \frac{1}{3} + ... + \frac{1}{3^{n}}}

Xem đáp án

Tử và mẫu là tổng các số hạng của cấp số nhân nên ta có:

$1 + \frac{1}{2} + ... + \frac{1}{2^{n}} = {\frac{1 - (\frac{1}{2})}{1 - \frac{1}{2}}}^{n + 1} = 2 [1 - {(\frac{1}{2})}^{n + 1}]$ .

$1 + \frac{1}{3} + ... + \frac{1}{3^{n}} = {\frac{1 - (\frac{1}{3})}{1 - \frac{1}{3}}}^{n + 1} = \frac{3}{2} [1 - {(\frac{1}{3})}^{n + 1}]$ .

$\Rightarrow \lim_{n \to \infty} \frac{1 + \frac{1}{2} + ... + \frac{1}{2^{n}}}{1 + \frac{1}{3} + ... + \frac{1}{3^{n}}} = \lim_{n \to \infty} \frac{2 [1 - {(\frac{1}{2})}^{n + 1}]}{\frac{3}{2} [1 - {(\frac{1}{3})}^{n + 1}]} = \frac{4}{3} \lim_{n \to \infty} \frac{1 - {(\frac{1}{2})}^{n + 1}}{1 - {(\frac{1}{3})}^{n + 1}} = \frac{4}{3}$ .

Vậy: $\lim_{n \to \infty} \frac{1 + \frac{1}{2} + ... + \frac{1}{2^{n}}}{1 + \frac{1}{3} + ... + \frac{1}{3^{n}}} = \frac{4}{3}$ .

Câu 37:

Cho hình lập phương ABCDA'B'C'D'. Gọi M,N,P lần lượt là trung điểm các cạnhAB, BC,C'D'. Tính góc giữa hai đường thẳng MN vàAP.

Xem đáp án

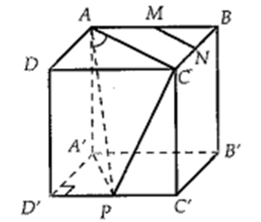
Giả sử hình lập phương có cạnh bằng a và $M N // A C$ nên: $(\hat{M N, A P}) = (\hat{A C, A P})$ .

Vì $Δ A^{'} D^{'} P$ vuông tại D' nên $A^{'} P = \sqrt{A^{'} {D^{'}}^{2} + D^{'} P^{2}} = \sqrt{a^{2} + {(\frac{a}{2})}^{2}} = \frac{a \sqrt{5}}{2}$ .

$Δ A A^{'} P$ vuông tại A' nên $A P = \sqrt{A^{'} A^{2} + A^{'} P^{2}} = \sqrt{a^{2} + {(\frac{a \sqrt{5}}{2})}^{2}} = \frac{3 a}{2}$ .

$Δ C C^{'} P$ vuông tại C' nên $C P = \sqrt{C {C^{'}}^{2} + C^{'} P^{2}} = \sqrt{a^{2} + \frac{a^{2}}{4}} = \frac{a \sqrt{5}}{2} .$

Ta có AC là đường chéo của hình vuông ABCD nên AC= $a \sqrt{2}$

Áp dụng định lý cosin trong tam giác ACP ta có:

$\begin{array}{l} C P^{2} = A C^{2} + A P^{2} - 2 A C . A P . c o s \hat{C A P} \\ \Rightarrow c o s \hat{C A P} = \frac{1}{\sqrt{2}} \\ \Rightarrow \hat{C A P} = 45 ° < 90 ° \end{array}$

Vậy $(\hat{A C; A P}) = \hat{C A P} = 45 °$ hay $(\hat{M N; A P}) = 45 °$ .

Câu 38:

Tùy theo giá trị của tham số m, tính giới hạn

\lim_{x \to - \infty} (\sqrt[3]{8 x^{3} + 5 x^{2} + 1} - \sqrt{9 x^{2} + 3 x + 5} + m x)

.

Xem đáp án

Tính giới hạn $\lim_{x \to - \infty} (\sqrt[3]{8 x^{3} + 5 x^{2} + 1} - \sqrt{9 x^{2} + 3 x + 5} + m x)$ .

.

§ Nếu m=-5 thì $\lim_{x \to - \infty} (\sqrt[3]{8 x^{3} + 5 x^{2} + 1} - \sqrt{9 x^{2} + 3 x + 5} - 5 x)$

$= \lim_{x \to - \infty} [(\sqrt[3]{8 x^{3} + 5 x^{2} + 1} - 2 x) - (\sqrt{9 x^{2} + 3 x + - 5} + 3 x)]$

$= \lim_{x \to - \infty} [\frac{{(\sqrt[3]{8 x^{3} + 5 x^{2} + 1})}^{3} - {(2 x)}^{3}}{{(\sqrt[3]{8 x^{3} + 5 x^{2} + 1})}^{2} + 2 x \cdot \sqrt[3]{8 x^{3} + 5 x^{2} + 1} + 4 x^{2}} - \frac{{(\sqrt{9 x^{2} + 3 x - 5})}^{2} - {(3 x)}^{2}}{\sqrt{9 x^{2} + 3 x - 5} - 3 x}]$

$= \lim_{x \to - \infty} [\frac{8 x^{3} + 5 x^{2} + 1 - 8 x^{3}}{{(\sqrt[3]{8 x^{3} + 5 x^{2} + 1})}^{2} + 2 x \cdot \sqrt[3]{8 x^{3} + 5 x^{2} + 1} + 4 x^{2}} - \frac{9 x^{2} + 3 x - 5 - 9 x^{2}}{|x| \cdot \sqrt{9 + \frac{3}{x} - \frac{5}{x^{2}}} - 3 x}]$

$= \lim_{x \to - \infty} [\frac{x^{2} (5 + \frac{1}{x^{2}})}{x^{2} [{(\sqrt[3]{8 + 5 \cdot \frac{1}{x} + \frac{1}{x^{3}}})}^{2} + 2 \sqrt[3]{8 + 5 \cdot \frac{1}{x} + \frac{1}{x^{3}}} + 4]} - \frac{x (3 - \frac{5}{x})}{- x (\sqrt{9 + \frac{3}{x} - \frac{5}{x^{2}}} + 3)}]$

$= \frac{5}{2 + 4 + 4} + \frac{3}{3 + 3}$

=1

§ Nếu $m < - 5$ thì $\lim_{x \to - \infty} (\sqrt[3]{8 x^{3} + 5 x^{2} + 1} - \sqrt{9 x^{2} + 3 x - 5} + m x)$

$= \lim_{x \to - \infty} [(\sqrt[3]{8 x^{3} + 5 x^{2} + 1} - 2 x) - (\sqrt{9 x^{2} + 3 x - 5} + 3 x) + (m + 5) x]$

$= + \infty$ .

§ Nếu m>-5 thì $\lim_{x \to - \infty} (\sqrt[3]{8 x^{3} + 5 x^{2} + 1} - \sqrt{9 x^{2} + 3 x - 5} + m x)$

$= \lim_{x \to - \infty} [(\sqrt[3]{8 x^{3} + 5 x^{2} + 1} - 2 x) - (\sqrt{9 x^{2} + 3 x - 5} + 3 x) + (m + 5) x]$

Câu 39:

Chứng minh phương trình $\frac{- c {os}^{2} x . \sin^{2} x + m \cos x - 3 m + 1}{\sin^{2} x - \cos x - 3} = m$ luôn có nghiệm với mọi $m > 1$

Xem đáp án

Lời giải

$\frac{c {os}^{2} x . \sin^{2} x - m \cos x + 3 m - 1}{\sin^{2} x + \cos x + 1} = m \Leftrightarrow \frac{- c {os}^{4} x + c {os}^{2} x - m \cos x + 3 m - 1}{- c {os}^{2} x + \cos x + 2} = m$ $\cos x \neq - 1$

Điều kiện: $\cos x \neq - 1$ .

Với điều kiện trên ta có

Phương trình $\Leftrightarrow \cos^{4} x - \cos^{2} x + m \cos x - 3 m + 1 = m (\cos^{2} x - \cos x - 2)$

$\Leftrightarrow c {os}^{4} x - (m + 1) c {os}^{2} x + 2 m \cos x - m + 1 = 0$ .

Xét hàm số $f (x) = c {os}^{4} x - (m + 1) c {os}^{2} x + 2 m \cos x - m + 1$ là hàm liên tục trên R nên cũng liên tục trên $[0; \frac{π}{2}]$ . Mặt khác $f (\frac{π}{2}) = 1 - m < 0$ (vì $m > 1$ ) và $f (0) = 1 - (m + 1) + 2 m - m + 1 = 1 > 0$ .

Suy ra: $f (0) . f (\frac{π}{2}) < 0$ .

Do đó phương trình f(x)=0 luôn có ít nhất một nghiệm $x_{0} \in (0; \frac{π}{2})$ (thỏa mãn điều kiện

Vậy phương trình $\frac{- c {os}^{2} x . \sin^{2} x + m \cos x - 3 m + 1}{\sin^{2} x - \cos x - 3} = m$ luôn có nghiệm với mọi $m > 1$ (đpcm)

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 16)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương