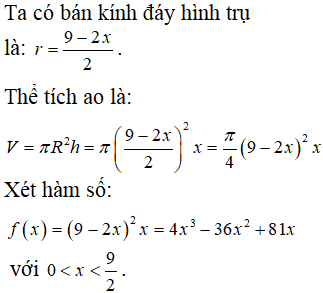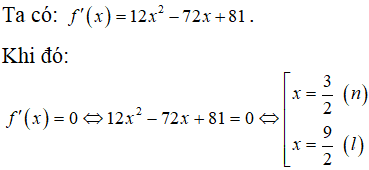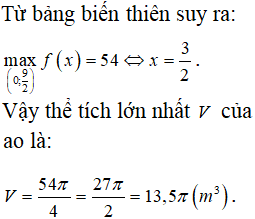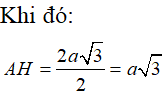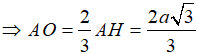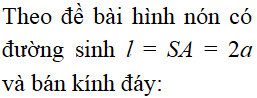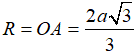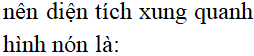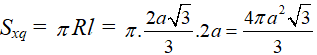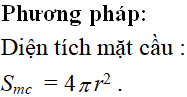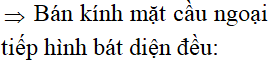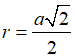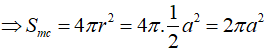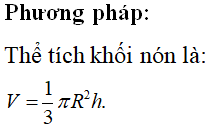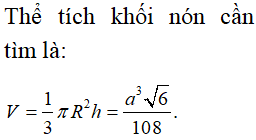40 câu hỏi trắc nghiệm thuộc 160 bài trắc nghiệm Mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P2) - qa.haylamdo.com

160 bài trắc nghiệm Mặt nón, mặt trụ, mặt cầu cực hay có lời giải

160 bài trắc nghiệm Mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P2)

1917 lượt thi
40 câu hỏi
50 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

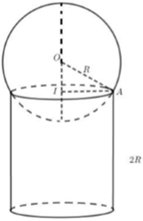
Một quả bóng bàn và một chiếc chén hình trụ có cùng chiều cao. Nếu ta đặt quả bóng lên miệng chiếc chén thấy phần ở ngoài của quả bóng có chiều cao bằng $\frac{3}{4}$ chiều cao của quả bóng. Gọi V₁ ,V₂ lần lượt là thể tích của quả bóng và thể tích chiếc chén, khi đó:

A. 3V₁ = 2V₂

B. 9V₁ = 8V₂

C. 27V₁ = 8V₂

D. 16V₁ = 9V₂

Chọn B.

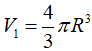
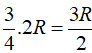
Xét tam giác vuông OIA có:

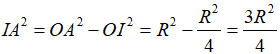
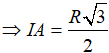
Thể tích khối trụ:

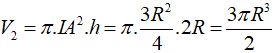
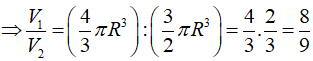
Câu 2:

Thể tích của miếng xúc xích dạng nửa hình trụ có đường kính đáy 2 cm và chiều cao 3 cm là:

A. $6 c m^{3}$

B. $\frac{3 π}{2} c m^{3}$

C. $6 π c m^{3}$

D. $\frac{3}{2} c m^{3}$

Chọn B.

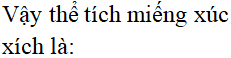
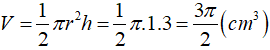
Câu 3:

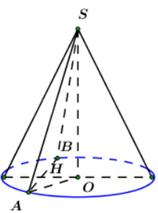
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SC = a , SB = 2a . Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABC. Góc giữa hai mặt phẳng (SBO) và (SBC) bằng:

A. 30⁰

B. 90⁰

C. 60⁰

D. 45⁰

Chọn D.

Câu 4:

Cho hình tứ diện đều cạnh 2a có một đỉnh trùng với đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón. Diện tích xung quanh của hình nón là:

A. $\frac{4 π a^{2} \sqrt{3}}{3}$

B. $2 π a^{2} \sqrt{3}$

C. $\frac{π a^{2} \sqrt{3}}{3}$

D. $\frac{8 π a^{2} \sqrt{3}}{3}$

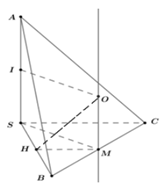
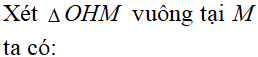
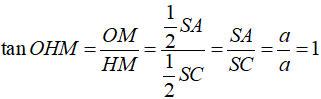
Câu 5:

Tính thể tích của khối nón biết thiết diện qua trục của nó là tam giác vuông cân có cạnh huyền bằng 2a.

A. $π a^{3}$

B. $\frac{2 π a^{3}}{3}$

C. $\frac{π a^{3}}{3}$

D. $2 π a^{3}$

Chọn C.

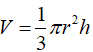
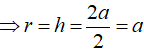
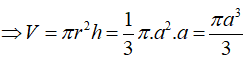
Câu 6:

Cho khối trụ có bán kính đáy r = $\sqrt{3}$ và chiều cao h = 4 . Tính thể tích V của khối trụ đã cho.

A. V= $12 π$

B. V= $\frac{16 π \sqrt{3}}{3}$

C. V= $16 π \sqrt{3}$

D. V= $4 π$

Chọn A.

Phương pháp:

Công thức tính thể tích khối trụ:

(với r là bán kính đáy, h là chiều cao của khối trụ.)

Cách giải:

Câu 7:

Tính diện tích mặt cầu ngoại tiếp hình bát diện đều có cạnh bằng a.

A. $\frac{2}{3} π a^{2}$

B. $\frac{1}{3} π a^{2}$

C. $π a^{2}$

D. $2 π a^{2}$

Chọn D.

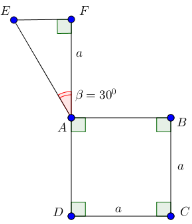
Câu 8:

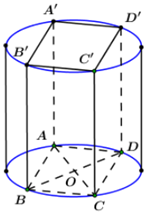
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Diện tích xung quanh của hình trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông ABCD và A'B'C'D' là:

A. $\sqrt{2} π a^{2}$

B. $2 π a^{2}$

C. $π a^{2}$

D. $2 \sqrt{2} π a^{2}$

Chọn A.

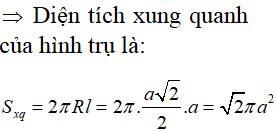
Câu 9:

Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2a, $∠ S A O = 30 °, ∠ S A B = 60 °$ . Diện tích xung quanh hình nón đã cho bằng:

A. $2 \sqrt{3} π a^{2}$

B. $\frac{3 \sqrt{2} π a^{2}}{4}$

C. $4 \sqrt{3} π a^{2}$

D. $3 \sqrt{2} π a^{2}$

Chọn C.

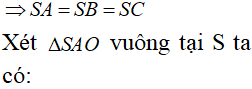
Câu 10:

Cho khối nón (N) có góc ở đỉnh bằng 90⁰ và diện tích xung quanh bằng 4 $\sqrt{2} π$ . Thể tích của khối nón đã cho bằng:

A. $\frac{8 π}{3}$

B. $\frac{4 π}{3}$

C. $8 π$

D. $4 π$

Chọn A.

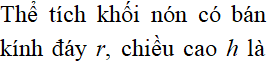
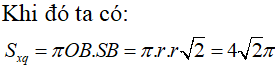
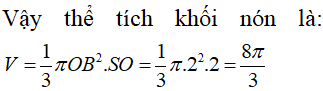
Câu 11:

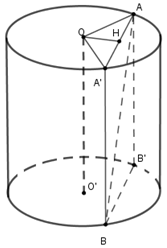
Cho hình trụ có tâm hai đáy lần lượt là O và O' ; bán kính đáy hình trụ bằng a.Trên hai đường tròn (O) và (O') lần lượt lấy hai điểm A và B sao cho đường thẳng AB tạo với trục của hình trụ một góc $30 °$ và có khoảng cách tới trục của hình trụ bằng $\frac{a \sqrt{3}}{2}$ .Tính diện tích toàn phần của hình trụ đã cho.

A. $\frac{π a^{2}}{3} (\sqrt{3} + 2)$

B. $π a^{2} (\sqrt{3} + 2)$

C. $2 π a^{2} (\sqrt{3} + 1)$

D. $\frac{2 π a^{2}}{3} (\sqrt{3} + 3)$

Chọn C.

Phương pháp:

+ Sử dụng:

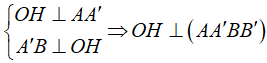
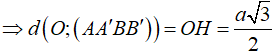
Câu 12:

Cho hình nón có thể tích bằng và diện tích xung quanh bằng $15 π$ .Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.

A. 4

B. 3

C. 6

D. 5.

Chọn B.

Phương pháp:

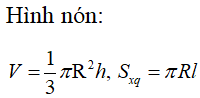
Cách giải:

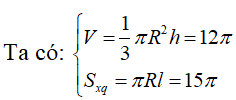
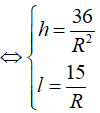
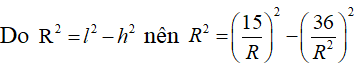
Câu 13:

Một khối trụ có bán kính đáy bằng 2 và khối cầu ngoại tiếp hình trụ có thể tích bằng $\frac{125 π}{6}$ .Tính thể tích khối trụ.

A. $2 \sqrt{41} π$

B. $6 π$

C. $12 π$

D. $\sqrt{41} π$

Chọn C.

Câu 14:

Tính theo a thể tích khối nón nội tiếp tứ diện đều cạnh a.

A. $\frac{\sqrt{6} π a^{3}}{27}$

B. $\frac{\sqrt{6} a^{3}}{108}$

C. $\frac{\sqrt{6} a^{3}}{27}$

D. $\frac{\sqrt{6} π a^{3}}{108}$

Chọn D.

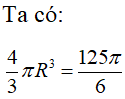
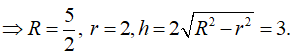
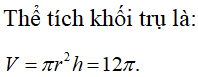
Câu 15:

Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và $∠ A B C = 120 °$ . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.

A. $\frac{a \sqrt{2}}{5}$

B. $a \sqrt{2}$

C. $a \sqrt{5}$

D. $\frac{a \sqrt{2}}{4}$

Đáp án B.

Dựng tam giác đều IAB (I và C cùng phía bờ AB).

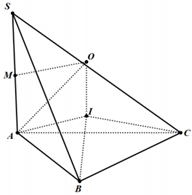
Ta có:

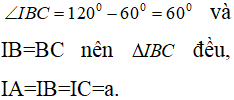
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.

Gọi M là trung điểm của SA.

Ta có:

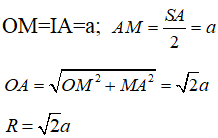
Câu 16:

Cho hình trụ có diện tích toàn phần là $8 π$ và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ?

A. $\frac{4 π}{9}$

B. $\frac{π \sqrt{6}}{9}$

C. $\frac{16 π \sqrt{3}}{9}$

D. $\frac{π \sqrt{6}}{12}$

Đáp án C

Gọi bán kính đường tròn đáy là r.

Vì thiết diện cắt bởi mặt phẳng qua trục là hình vuông nên chiều cao hình trụ là 2r.

Ta có:

Theo đề bài:

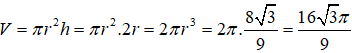
Câu 17:

Tính thể tích V của khối nón có bán kính đáy bằng 3 và chiều cao bằng 6.

A. $V = 18 π$

B. $V = 54 π$

C. $V = 108 π$

D. $V = 36 π$

Đáp án A.

Câu 18:

Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ hộp ít nhất (diện tích toàn phần của lon nhỏ nhất). Bán kính đáy của vỏ lon là bao nhiêu khi muốn thể tích của lon là 314 $c m^{3}$ .

A. $r = \sqrt[3]{\frac{314}{4 π}} c m$

B. $r = 942 \sqrt[3]{2 π} c m$

C. $r = \sqrt[3]{\frac{314}{2 π}} c m$

D. $r = \sqrt[3]{\frac{314}{π}} c m$

Diện tích toàn phần của lon:

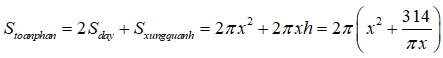
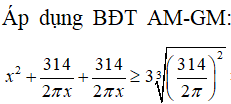
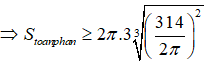
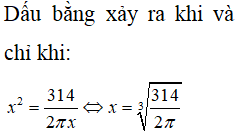
Câu 19:

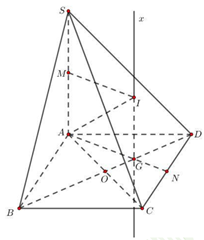
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc $∠ A B C = 60 °$ , cạnh bên SA=a và vuông góc với mặt đáy. Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ACD.

A. $R = \frac{a \sqrt{5}}{2}$

B. $R = a$

C. $R = \frac{a \sqrt{7}}{12}$

D. $R = \frac{a}{2}$

Chọn C.

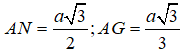
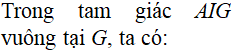
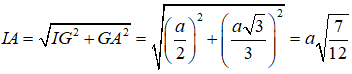
Câu 20:

Cho khối cầu có thể tích bằng $\frac{8 π a^{3} \sqrt{6}}{27}$ , khi đó bán kính R của mặt cầu là:

A. $R = \frac{a \sqrt{2}}{3}$

B. $R = \frac{a \sqrt{6}}{2}$

C. $R = \frac{a \sqrt{3}}{3}$

D. $R = \frac{a \sqrt{6}}{3}$

Chọn D.

Thể tích khối cầu:

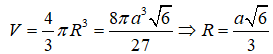
Câu 21:

Cho khối nón có bán kính đáy $r = \sqrt{3}$ và chiều cao h=4. Tính thể tích V của khối nón đã cho.

A. $V = 4 π$

B. $V = 16 π \sqrt{3}$

C. $V = 12 π$

D. $V = \frac{16 π \sqrt{3}}{3}$

Đáp án A.

Ta có:

Câu 22:

Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF:

A. $\frac{10 π}{7} a^{3}$

B. $\frac{π}{3} a^{3}$

C. $\frac{5 π}{2} a^{3}$

D. $\frac{10 π}{9} a^{3}$

Câu 23:

Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân, cạnh huyền bằng $a \sqrt{2}$ . Thể tích khối nón là:

A. $\frac{π \sqrt{2}}{6} a^{3}$

B. $\frac{π \sqrt{2}}{12} a^{3}$

C. $\frac{π \sqrt{2}}{4} a^{3}$

D. $\frac{π \sqrt{2}}{12} a^{2}$

Đáp án B.

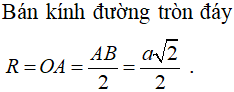
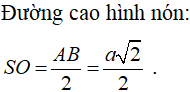
Thể tích khối nón:

Câu 24:

Cho ba hình cầu tiếp xúc ngoài nhau từng đôi một và cùng tiếp xúc với một mặt phẳng. Các tiếp điểm của các hình cầu trên mặt phẳng lập thành tam giác có các cạnh bằng 4 , 2 và 3. Tích bán kính của ba hình cầu trên là:

A. 12

B. 3

C. 6

D. 9

Đáp án B.

Gọi O₁, O₂, O₃ lần lượt là tâm của 3 mặt cầu và A, B, C lần lượt là hình chiếu của 3 tâm trên mặt phẳng đã cho.

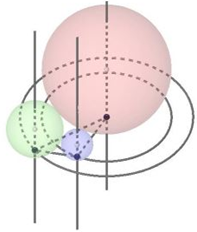
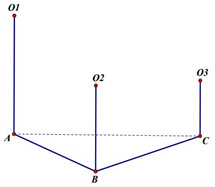
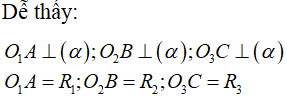
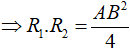
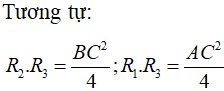
Câu 25:

Một hình trụ có bán kính đáy r = a độ dài đường sinh l = 2a. Diện tích toàn phần của hình trụ này là:

A. $2 π a^{2}$

B. $4 π a^{2}$

C. $6 π a^{2}$

D. $5 π a^{2}$

Đáp án C.

Câu 26:

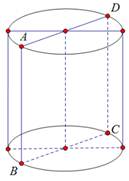
Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 30cm² và chu vi bằng 26cm . Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ (T). Diện tích toàn phần của (T) là:

A. $23 π (c m^{2})$

B. $\frac{23 π}{2} (c m^{2})$

C. $\frac{69 π}{2} (c m^{2})$

D. $69 π (c m^{2})$

Đáp án C.

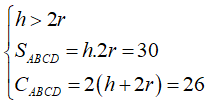
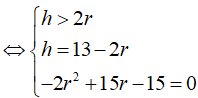
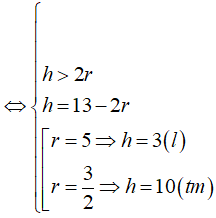
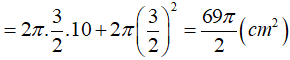
Câu 27:

Khối nón có bán kính (N) đáy bằng và 3 diện tích xung quanh bằng. Tính 15p thể tích V của khối nón (N):

A. $V = 36 π$

B. $V = 60 π$

C. $V = 30 π$

D. $V = 12 π$

Đáp án D.

Ta có :

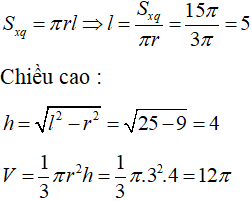
Câu 28:

Một chiếc thùng đựng nước có hình của một khối lập phương chứa đầy nước . Đặt vào trong thùng đó một khối có dạng nón sao cho đỉnh trùng với tâm một mặt của lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước trào ra ngoài và lượng nước còn lại ở trong thùng.

A. $\frac{π}{12 - π}$

B. $\frac{1}{11}$

C. $\frac{π}{12}$

D. $\frac{11}{12}$

Đáp án A.

Coi khối lập phương có cạnh 1.

Thể tích khối lập phương là V = 1

Từ giả thiết ta suy ra khối nón có chiều cao h=1, bán kính đáy r=1/2

Thể tích lượng nước trào ra ngoài là thể tích V₁ của khối nón.

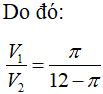
Câu 29:

Thể tích của khối cầu bán kính a bằng:

A. $\frac{4 π a^{3}}{3}$

B. $4 π a^{3}$

C. $\frac{π a^{3}}{3}$

D. $2 π a^{3}$

Đáp án A.

Phương pháp:

Thể tích khối cầu bán kính R là:

Cách giải:

Thể tích khối cầu bán kính R=3 là:

Câu 30:

Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng:

A. $\frac{\sqrt{3} π a^{3}}{3}$

B. $\frac{\sqrt{3} π a^{3}}{2}$

C. $\frac{2 π a^{3}}{3}$

D. $\frac{π a^{3}}{3}$

Đáp án A.

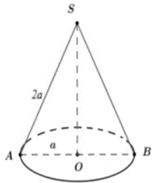
Cách giải:

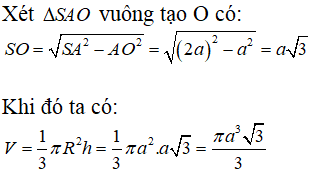
Câu 31:

Một khối đồ chơi gồm hai khối trụ (H₁),(H₂) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là r₁,h₁,r₂,h₂, $r_{2} = \frac{1}{2} r_{1}, h_{2} = 2 h_{1}$ thỏa mãn (tham khảo hình vẽ).

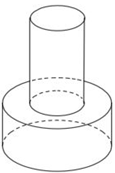
Biết rằng thể tích của toàn bộ khối đồ chơi bằng 30cm³, thể tích khối trụ (H₁) bằng:

A. 24cm³

B. 15cm³

C. 20cm³

D. 10cm³

Đáp án C.

Vậy thể tích khối trụ (H₁) là 20 cm³

Câu 32:

Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán kính a. Khi đó thể tích của hình trụ bằng:

A. Sa

B. $\frac{1}{2}$ Sa

C. $\frac{1}{3}$ Sa

D. $\frac{1}{4}$ Sa

Chọn A.

Gọi r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.

Theo bài ra ta có:

$\{\begin{cases} S = 2 π r h \\ π r^{2} = 4 π a^{2} \end{cases} \Leftrightarrow \{\begin{cases} r = 2 a \\ h = \frac{S}{4 π a} \end{cases}$

Thể tích khối trụ là:

$V = π r^{2} h = π 4 a^{2} \cdot \frac{S}{4 π a} = S a$

Câu 33:

Cho hình nón có chiều cao h và góc ở đỉnh bằng $90 °$ . Thể tích của khối nón xác định bởi hình nón trên:

A. $\frac{2 π h^{3}}{3}$

B. $\frac{6 π h^{3}}{3}$

C. $\frac{π h^{3}}{3}$

D. $2 π h^{3}$

Chọn C.

Từ giả thiết suy ra bán kính nón r = h.

Vậy thể tích khối nón tương ứng là:

$V = \frac{1}{3} π r^{2} h = \frac{π h^{3}}{3}$

Câu 34:

Quay hình chữ nhật ABCD quanh trục AB cố định, đường gấp khúc ADBC cho ta hình trụ (T). Gọi tam giác MNP là tam giác đều nội tiếp đường tròn đáy (không chứa điểm A). Tính tỷ số giữa thể tích khối trụ và thể tích khối chóp A.MNP.

A. $\frac{4}{3 \sqrt{3}} π$

B. $\frac{4}{\sqrt{3}} π$

C. $\frac{\sqrt{3}}{4} π$

D. $\frac{4}{3} π$

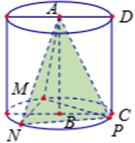
Chọn B.

Hình trụ (T) có bán kính r = BC và chiều cao h = CD.

Thể tích khối trụ là:

$V = π r^{2} h$

Gọi cạnh của tam giác MNP là x, khi đó bán kính đường tròn ngoại tiếp tam giác MNP là:

$r = \frac{2}{3} \cdot \frac{x \sqrt{3}}{2} \Leftrightarrow x = r \sqrt{3}$

Khối chóp A.MNP có đáy tam giác MNP đều và chiều cao AB = DC = h.

Thể tích của khối chóp:

$V^{'} = \frac{1}{3} A B . S_{△ M N P} = \frac{1}{3} . h . \frac{{(r \sqrt{3})}^{2} \sqrt{3}}{4} = \frac{\sqrt{3} r^{2} h}{4}$

Tỷ số giữa thể tích khối trụ và thể tích khối chóp A.MNP là:

$\frac{V^{'}}{V} = \frac{π r^{2} h}{\frac{\sqrt{3} r^{2} h}{4}} = \frac{4 π}{\sqrt{3}}$

Câu 35:

Phương trình nào sau đây là phương trình của đường tròn tâm $I (- 1; 2)$ , bán kính bằng 3?

A. ${(x - 1)}^{2} + {(y + 2)}^{2} = 9$

B. ${(x + 1)}^{2} + {(y + 2)}^{2} = 9$

C. ${(x - 1)}^{2} + {(y - 2)}^{2} = 9$

D. ${(x + 1)}^{2} + {(y - 2)}^{2} = 9$

Chọn D.

Câu 36:

Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với AB=AC=a, $∠ B A C = 120 °$ , mặt phẳng (A’BC’) tạo với đáy một góc $60 °$ . Tính thể tích của khối lăng trụ đã cho bằng:

A. $\frac{3 \sqrt{3} a^{3}}{8}$

B. $\frac{9 a^{3}}{8}$

C. $\frac{a^{3} \sqrt{3}}{8}$

D. $\frac{3 a^{3}}{8}$

Chọn A.

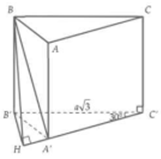
Ta có:

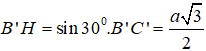
Câu 37:

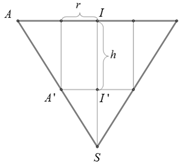
Khi sản xuất hộp mì tôm các nhà sản xuất luôn để một khoảng trống dưới đáy hộp. Hình vẽ dưới mô tả cấu trúc của hộp mì tôm. Thớ mì tôm có dạng hình trụ, hộp mì có dạng hình nón cụt được cắt ra bởi hình nón có chiều cao và bán kính đáy . Nhà sản xuất tìm cách sao cho thớ mì tôm có được thể tích lớn nhất vì mục đích thu hút khách hàng. Tìm thể tích lớn nhất đó.

A. $48 π$

B. $\frac{81}{2} π$

C. $36 π$

D. $54 π$

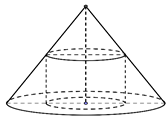
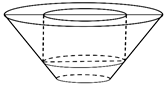
Chọn A.

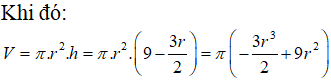
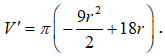
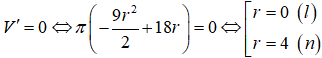
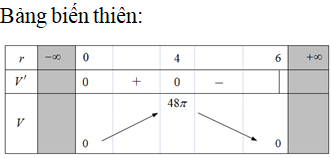
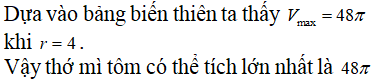
Câu 38:

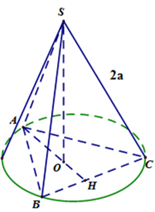
Tại trung tâm một thành phố người ta tạo điểm nhấn bằng cột trang trí hình nón có kích thước như sau: chiều dài đường sinh , bán kính đáy . Biết rằng tam giác là thiết diện qua trục của hình nón và là trung điểm . Trang trí một hệ thống đèn điện tử chạy từ đến trên mặt nón. Xác định giá trị ngắn nhất của chiều dài dây đèn điện tử.

A. $10 m$

B. $15 m$

C. $5 \sqrt{5} m$

D. $5 \sqrt{3} m$

Chọn C.

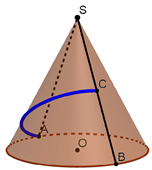
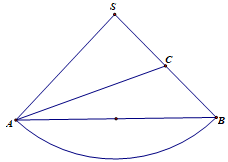
Câu 39:

Cho một hình cầu nội tiếp hình nón tròn xoay có góc ở đỉnh là $2 α$ , bán kính đáy là R và chiều cao là h. Một hình trụ ngoại tiếp hình cầu đó có đáy dưới nằm trong mặt phẳng đáy của hình nón (tham khảo hình vẽ). Gọi $V_{1}, V_{2}$ lần lượt là thể tích của hình nón và hình trụ, biết rằng $V_{1} \neq V_{2}$ . Gọi là giá trị lớn nhất của tỉ số $\frac{V_{2}}{V_{1}}$ . Giá trị của biểu thức P=48M+25 thuộc khoảng nào dưới đây?

A. (40;60)

B. (60,80)

C. (20,40)

D. (0,20)

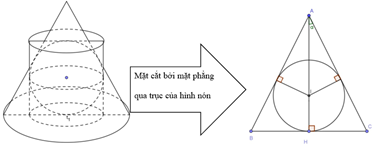
Chọn B.

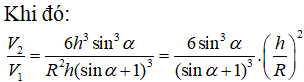
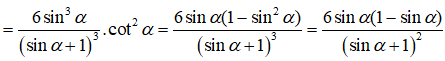
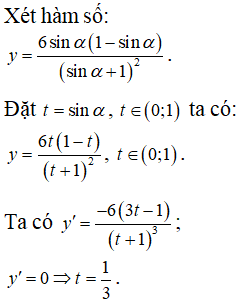
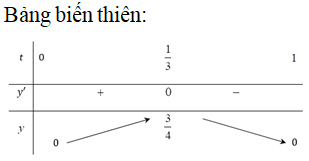
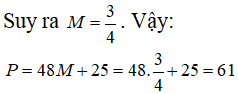
Câu 40:

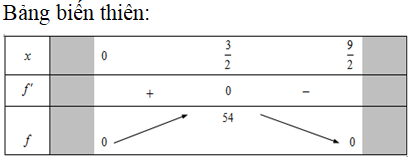
Trên một mảnh đất hình vuông có diện tích $81 m^{2}$ người ta đào một cái ao nuôi cá hình trụ (như hình vẽ) sao cho tâm của hình tròn đáy trùng với tâm của mảnh đất. Ở giữa mép ao và mép mảnh đất người ta để lại một khoảng đất trống để đi lại, biết khoảng cách nhỏ nhất giữa mép ao và mép mảnh đất là x(m). Giả sử chiều sâu của ao cũng là x(m). Tính thể tích lớn nhất của ao.

A. $V = 13, 5 π (c m^{3})$

B. $V = 27 π (c m^{3})$

C. $V = 36 π (c m^{3})$

D. $V = 72 π (c m^{3})$

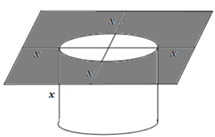
Chọn A.

Bắt đầu thi ngay

Bài thi liên quan