40 câu hỏi trắc nghiệm thuộc 299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P4)

Câu 1:

Gọi T là tổng các nghiệm của phương trình $l o {g^{2}}_{3} x - 3 l o g_{3} x + 6 = 0$ , tính T

A.5

B.-3

C.36

D. $\frac{1}{243}$

Xem đáp án

Chọn C

Câu 2:

Phương trình $4^{x} - m . 2^{x + 1} + 2 m = 0$ có hai nghiệm $x_{1}, x_{2}$ thỏa mãn $x_{1} + x_{2} = 3$ khi m bằng bao nhiêu?

A. 4

B. 3

C. 2

D. 1

Xem đáp án

Chọn A

Câu 3:

Có bao nhiêu giá trị nguyên của m để phương trình

$9 . 3^{2 x} - m (4 \sqrt[4]{x^{2} + 2 x + 1} + 3 m + 3)$ $. 3^{x} + 1 = 0$ có đúng 3 nghiệm thực phân biệt

A. Vô số

B. 3

C. 1

D. 2

Xem đáp án

Câu 4:

Phương trình

$2^{x - 2 + \sqrt[3]{m - 3 x}} + (x^{3} - 6 x^{2} + 9 x + m) 2^{x - 2}$ $= 2^{x - 2} + 1$ có 3 nghiệm phân biệt khi và chỉ khi $m \in (a; b)$ . Tính giá trị biểu thức

A.36

B.48

C.64

D.72

Xem đáp án

Câu 5:

Giả sử phương trình $\log_{2}^{2} x - (m + 2) l o g_{2} x + 2 m = 0$ có hai nghiệm thực phân biệt $x_{1}, x_{2}$ thỏa mãn $x_{1} + x_{2} = 6$ . Giá trị của biểu thức $|x_{1} - x_{2}|$ là

A.3

B.8

C.2

D.4

Xem đáp án

Chọn C

Đặt $\log_{2} x = t \Leftrightarrow x = 2^{t}$

PT trở thành

$t^{2} - (m + 2) t + 2 m = 0 \Leftrightarrow \{\begin{cases} t_{1} = 2 \\ t_{2} = m \end{cases} \Rightarrow \{\begin{cases} x_{1} = 4 \\ x_{2} = 2^{m} \end{cases} T h e o đ ề b à i x_{1} + x_{2} = 6 \Leftrightarrow 4 + 2^{m} = 6 \Leftrightarrow m = 1 \Rightarrow x_{2} = 2 \Rightarrow |x_{1} - x_{2}| = |4 - 2| = 2$

Câu 6:

Có bao nhiêu giá trị nguyên của m để phương trình $(m + 1) 16^{x} - 2 (2 m - 3) 4^{x} + 6 m + 5 = 0$ có hai nghiệm trái dấu?

A.1

B.2

C.3

D.0

Xem đáp án

Chọn B

Câu 7:

Cho phương trình ${(\sqrt{2 - \sqrt{3}})}^{x} + {(\sqrt{2 + \sqrt{3}})}^{x} = 4$ . Gọi $x_{1}, x_{2} (x_{1} < x_{2})$ là hai nghiệm thực của phương trình. Khẳng định nào sau đây là đúng?

Xem đáp án

Chọn A

${(\sqrt{2 - \sqrt{3}})}^{x} + {(\sqrt{2 + \sqrt{3}})}^{x} = 4 \Leftrightarrow \frac{1}{{(\sqrt{2 + \sqrt{3}})}^{x}} + {(\sqrt{2 + \sqrt{3}})}^{x} = 4 \Leftrightarrow {(\sqrt{2 + \sqrt{3}})}^{2 x} - 4 {(\sqrt{2 + \sqrt{3}})}^{x} + 1 = 0 \Leftrightarrow \{\begin{cases} {(\sqrt{2 + \sqrt{3}})}^{x} = 2 + \sqrt{3} \\ {(\sqrt{2 + \sqrt{3}})}^{x} = 2 - \sqrt{3} \end{cases} \Leftrightarrow \{\begin{array}{l} \frac{x_{1}}{2} = 1 \\ \frac{x_{2}}{2} = - 1 \end{array} \Leftrightarrow \{\begin{cases} x_{1} = 2 \\ x_{2} = - 2 \end{cases} \Rightarrow x_{1} + x_{2} = 0$

Câu 8:

Tìm tất cả các giá trị của tham số m để phương trình $l o {g^{2}}_{2} x + l o g_{2} x + m = 0$ có nghiệm $x \in (0; 1)$

Xem đáp án

Chọn A

$Đ ặ t \log_{2} x = t . D o 0 < x < 1 n ê n t < 0 B à i t o á n t r ở t h à n h t ì m c á c g i á t r ị t đ ể P T t^{2} + t + m = 0 (*) c ó n g h i ệ m v ớ i m ọ i t < 0 (*) \Leftrightarrow t^{2} + t = - m Đ ặ t f (t) = t^{2} + t = {(t + \frac{1}{2})}^{2} - \frac{1}{4} D ễ t h ấ y \underset{(- \infty; 0)}{m i n f (t)} = \frac{- 1}{4} k h i t = \frac{- 1}{2} V ậ y P T c ó n g h i ệ m k h i - m \geq \frac{- 1}{4} \Leftrightarrow m \leq \frac{1}{4}$

Câu 9:

Với giá trị nào của tham số m thì phương trình $4^{x} - m . 2^{x + 1} + 2 m = 0$ có hai nghiệm $x_{1}, x_{2}$ thoả mãn $x_{1} + x_{2} = 3$

A.1

B.4

C.2

D.3

Xem đáp án

Câu 10:

Có bao nhiêu giá trị nguyên của tham số m để $4^{x} - m 2^{x + 1} + 5 - m = 0$ có hai nghiệm phân biệt?

A. 1

B. 4

C. 3

D. 6

Xem đáp án

$4^{x} - m . 2^{x + 1} + 5 - m = 0 \Leftrightarrow {(2^{x})}^{2} - 2 m . 2^{x} + 5 - m = 0 (*) Đ ặ t 2^{x} = t (t > 0) . P T t r ở t h à n h : t^{2} - 2 m t + 5 - m = 0 (1) Đ ể P T (*) c ó 2 n g h i ệ m p h â n b i ệ t t h ì P T (1) p h ả i c ó 2 n g h i ệ m p h â n b i ệ t d ư ơ n g \Leftrightarrow \{\begin{cases} ∆' > 0 \\ 2 m > 0 \\ 5 - m > 0 \end{cases} \Leftrightarrow \{\begin{cases} m^{2} + m - 5 > 0 \\ m > 0 \\ m < 5 \end{cases} \Leftrightarrow \{\begin{cases} m \in (- \infty; \frac{- 1 - \sqrt{21}}{2}) \cup (\frac{- 1 + \sqrt{21}}{2}; + \infty) \\ 0 < m < 5 \end{cases} \Leftrightarrow \frac{- 1 + \sqrt{21}}{2} < m < 5 D o m \in ℤ n ê n m = {2; 3; 4}$

Câu 11:

Có bao nhiêu giá trị nguyên của tham số m để phương trình $4^{x} - (m + 2018) 2^{x} + (2019 + 3 m) = 0$ có hai nghiệm trái dấu?

A.670

B.671

C.672

D.673

Xem đáp án

$4^{x} - (m + 2018) . 2^{x} + 2019 + 3 m = 0 \Leftrightarrow {(2^{x})}^{2} - (m + 2018) . 2^{x} + 2019 + 3 m = 0 Đ ặ t 2^{x} = t (t > 0) . P T t r ở t h à n h t^{2} - (m + 2018) t + 2019 + 3 m = 0 Đ K đ ể p h ư ơ n g t r ì n h c ó 2 n g h i ệ m p h â n b i ệ t \Leftrightarrow \{\begin{cases} ∆ > 0 \\ m + 2018 > 0 \\ 3 m + 2019 > 0 \end{cases} \Leftrightarrow \{\begin{cases} {(m + 2018)}^{2} - 4 (3 m + 2019) > 0 \\ m > - 2018 \\ m > \frac{- 2019}{3} \end{cases} \Leftrightarrow \{\begin{cases} m^{2} + 4024 m + 4064248 > 0 (l u ô n đ ú n g) \\ m > \frac{- 2019}{3} \end{cases} K h i đ ó \{\begin{cases} 2^{x_{1}} = t_{1} \\ 2^{x_{2}} = t_{2} \end{cases} T h e o đ ề b à i x_{1} x_{2} < 0 \Rightarrow 0 < t_{1} < 1 < t_{2} \Rightarrow (t_{1} - 1) (t_{2} - 1) < 0 \Leftrightarrow t_{1} t_{2} + 1 - (t_{1} + t_{2}) < 0 Á p d ụ n g V i - é t t a c ó : 3 m + 2019 + 1 - (m + 2018) < 0 \Leftrightarrow 2 m < - 2 \Leftrightarrow m < - 1 K ế t h ợ p Đ K t a c ó \frac{- 2019}{3} < m < - 1 V ậ y c ó 671 g i á t r ị n g u y ê n c ủ a m t h ỏ a m ã n b à i t o á n$ Chọn B

Câu 12:

Có bao nhiêu giá trị nguyên của tham số m để phương trình: $4^{x} - (m + 3) . 2^{x + 1} + m + 9 = 0$ có hai nghiệm dương phân biệt

A.3

B.4

C.5

D. Vô số

Xem đáp án

Chọn A

$4^{x} - (m + 3) . 2^{x + 1} + m + 9 = 0 \Leftrightarrow {(2^{x})}^{2} - 2 (m + 3) . 2^{x} + m + 9 = 0 (*) Đ ặ t 2^{x} = t (t > 0) . P T t r ở t h à n h t^{2} - 2 (m + 3) t + m + 9 = 0 (1) P T (*) c ó 2 n g h i ệ m p h â n b i ệ t k h i P T (1) c ó 2 n g h i ệ m d ư ơ n g p h â n b i ệ t \Rightarrow \{\begin{array}{l} ∆' > 0 \\ S > 0 \\ P > 0 \end{array} \Leftrightarrow \{\begin{cases} {(m + 3)}^{2} - m - 9 > 0 \\ 2 (m + 3) > 0 \\ m + 9 > 0 \end{cases} \Leftrightarrow \{\begin{array}{l} m^{2} + 5 m > 0 \\ m > - 3 \\ m > - 9 \end{array} \Leftrightarrow \{\begin{cases} m \in (- \infty; - 5) \cup (0; + \infty) \\ m > - 3 \end{cases} \Leftrightarrow m > 0 T h e o đ ề b à i x_{1} x_{2} > 0 \Leftrightarrow 1 < t_{1} < t_{2} \Leftrightarrow (t_{1} - 1) (t_{2} - 1) > 0 \Leftrightarrow t_{1} t_{2} - (t_{1} + t_{2}) + 1 > 0 á p d ụ n g V i - é t t a c ó : m + 9 - 2 (m + 3) + 1 > 0 \Leftrightarrow - m + 4 > 0 \Leftrightarrow m < 4 K ế t h ợ p Đ K t a đ ư ợ c 0 < m < 4 K L : c ó 3 g i á t r ị n g u y ê n c ủ a m t h ỏ a m ã n y ê u c ầ u b à i t o á n$

Câu 13:

Tìm tập nghiệm của phương trình $4^{x + 1} - 3 . 2^{x} - 1 = 0$ là

Xem đáp án

Chọn D

Câu 14:

Cho phương trình $4^{x} - 2^{x + 2} + m - 2 = 0$ với m là tham số. Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn $0 \leq x_{1} < x_{2}$

A.1

B.3

C.2

D.0

Xem đáp án

Chọn A

$Đ ặ t 2^{x} = t (t > 0) \Leftrightarrow x = \log_{2} t . P T t r ở t h à n h t^{2} - 4 t + m - 2 = 0 P T c ó 2 n g h i ệ m p h â n b i ệ t \Leftrightarrow \{\begin{cases} ∆' > 0 \\ S > 0 \\ P > 0 \end{cases} \Leftrightarrow \{\begin{array}{l} 4 - m + 2 > 0 \\ 4 > 0 \\ m - 2 > 0 \end{array} \Leftrightarrow \{\begin{array}{l} m < 6 \\ m > 2 \end{array} \Leftrightarrow 2 < m < 6 T h e o Đ B 0 \leq x_{1} < x_{2} \Rightarrow 1 \leq t_{1} < t_{2} \Leftrightarrow (t_{1} - 1) (t_{2} - 1) \geq 0 \Leftrightarrow t_{1} t_{2} + 1 - (t_{1} + t_{2}) \geq 0 . Á p d ụ n g V i - é t t a c ó : m - 2 + 1 - 4 \geq 0 \Leftrightarrow m \geq 5 K ế t h ợ p t a đ ư ợ c 5 \leq m < 6 V ậ y c h ỉ c ó 1 g i á t r ị n g u y ê n c ủ a m l à m = 5 T M b à i t o á n$

Câu 15:

Cho a,b là các số thực dương thỏa mãn $\log_{4} a = \log_{6} b = \log_{9} (a + b)$ . Giá trị của $\frac{a}{b}$ bằng

A. $\frac{3}{2}$

B. $\frac{2}{3}$

C. $\frac{\sqrt{5} + 1}{2}$

D. $\frac{\sqrt{5} - 1}{2}$

Xem đáp án

Chọn D

Câu 16:

Giả sử phương trình $l o {g^{2}}_{2} 2 x - 3 l o g_{2} x - 2 = 0$ có một nghiệm dạng $x = 2^{\frac{a + \sqrt{b}}{c}}$ với $a, b, c \in ℤ^{+}$ và $b < 20$ . Tính tổng $a + b + c^{2}$

A. 10

B. 11

C. 18

D. 27

Xem đáp án

Chọn A

Câu 17:

Tìm tất cả các giá trị thực của m để phương trình $\log^{2} |\cos x| - m . \log \cos^{2} x$ $- m^{2} + 4 = 0$ vô nghiệm

Xem đáp án

Chọn C

Câu 18:

Cho phương trình ${\log^{2}}_{2} x - 2 \log_{2} x - \sqrt{m + \log_{2} x} = m (*)$ . Có bao nhiêu giá trị nguyên của tham số $m \in [- 2019; 2019]$ để phương trình (*) có nghiệm?

A.2021

B.2019

C.4038

D.2020

Xem đáp án

$X é t P T : \sqrt{m + \log_{2} x} = \log_{2} x - 1 (1) \Leftrightarrow \log_{2}^{2} x - 3 \log_{2} x + 1 - m = 0 P T c ó n g h i ệ m \Leftrightarrow ∆ \geq 0 \Leftrightarrow 9 - 4 (1 - m) \geq 0 \Leftrightarrow 5 + 4 m \geq 0 \Leftrightarrow m \geq \frac{- 5}{4} X é t P T \sqrt{m + \log_{2} x} = - \log_{2} x (2) \Leftrightarrow l {og}_{2}^{2} x - \log_{2} x - m = 0 P T c ó n g h i ệ m \Leftrightarrow ∆ \geq 0 \Leftrightarrow 1 + 4 m \geq 0 \Leftrightarrow m \geq \frac{- 1}{4} Đ ể P t (*) c ó n g h i ệ m t h ì í t n h ấ t m ộ t t r o n g 2 P T (1) h o ặ c (2) p h ả i c ó n g h i ệ m T ừ đ ề b à i t a s u y r a \frac{- 5}{4} \leq m \leq 2019 V ậ y c ó \frac{2019 + 1}{1} + 1 = 2021 g i á t r ị n g u y ê n c ủ a m t h ỏ a m ã n b à i t o á n$

Câu 19:

Có bao nhiêu giá trị nguyên của m để phương trình $16^{x} - 2 (m + 1) . 4^{x} + 3 m - 8 = 0$ có hai nghiệm trái dấu

A. 6

B. 7

C. 0

D. 3

Xem đáp án

Chọn A

$16^{x} - 2 (m + 1) . 4^{x} + 3 m - 8 = 0 \Leftrightarrow {(4^{x})}^{2} - 2 (m + 1) . 4^{x} + 3 m - 8 = 0 (*) Đ ặ t 4^{x} = t (t > 0) P T (*) t r ở t h à n h t^{2} - 2 (m + 1) t + 3 m - 8 = 0 (1) P T (*) c ó 2 n g h i ệ m p h â n b i ệ t k h i P T (1) c ó 2 n g h i ệ m p h â n b i ệ t d ư ơ n g \Leftrightarrow \{\begin{array}{l} ∆' > 0 \\ S > 0 \\ P > 0 \end{array} \Leftrightarrow \{\begin{cases} {(m + 1)}^{2} - 3 m + 8 > 0 \\ 2 (m + 1) > 0 \\ 3 m - 8 > 0 \end{cases} \Leftrightarrow \{\begin{array}{l} m^{2} - m + 9 > 0 (l u ô n đ ú n g) \\ m > - 1 \\ m > \frac{8}{3} \end{array} \Leftrightarrow m > \frac{8}{3} K h i đ ó \{\begin{cases} 4^{x_{1}} = t_{1} \\ 4^{x_{2}} = t_{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = \log_{4} t_{1} \\ x_{2} = \log_{4} t_{2} \end{cases} T h e o Đ B : x_{1} x_{2} < 0 \Rightarrow 0 < t_{1} < 1 < t_{2} \Rightarrow (t_{1} - 1) (t_{2} - 1) < 0 \Leftrightarrow t_{1} t_{2} + 1 - (t_{1} + t_{2}) < 0 Á p d ụ n g V i - é t t a đ ư ợ c : 3 m - 8 + 1 - 2 (m + 1) < 0 \Leftrightarrow m < 9 K ế t h ợ p Đ K t a c ó \frac{8}{3} < m < 9 \Rightarrow m \in {3; 4; 5; 6; 7; 8} V ậ y c ó 6 g i á t r ị n g u y ê n c ủ a m$

Câu 20:

Biết rằng phương trình $l o {g^{2}}_{3} x - (m + 2) l o g_{3} x + 3 m - 1 = 0$ có hai nghiệm $x_{1}, x_{2}$ thảo mãn $x_{1} . x_{2} = 27$ . Khi đó tổng $x_{1} + x_{2}$ bằng

A. 6

B. 12

C. $\frac{1}{3}$

D. $\frac{34}{3}$

Xem đáp án

Chọn B

Câu 21:

Có bao nhiêu giá trị nguyên của tham số m để phương trình $16^{x} - 2 (m + 1) 4^{x} + 3 m - 8 = 0$ có hai nghiệm trái dấu?

A.6

B.7

C.0

D.3

Xem đáp án

Chọn A

Câu 22:

Tìm tất cả các giá trị thực của tham số m để phương trình $9^{x} - m . 3^{x} + 2 m - 5 = 0$ có hai nghiệm trái dấu

Xem đáp án

$9^{x} - m . 3^{x} + 2 m - 5 = 0 \Leftrightarrow {(3^{x})}^{2} - m . 3^{x} + 2 m - 5 = 0 (*) Đ ặ t 3^{x} = t (t > 0) P T (*) t r ở t h à n h : t^{2} - m t + 2 m - 5 = 0 (1) P T (*) c ó 2 n g h i ệ m p h â n b i ệ t \Leftrightarrow P T (1) c ó 2 n g h i ệ m p h â n b i ệ t d ư ơ n g \Leftrightarrow \{\begin{cases} ∆ > 0 \\ S > 0 \\ P > 0 \end{cases} \Leftrightarrow \{\begin{cases} m^{2} - 4 (2 m - 5) > 0 \\ m > 0 \\ 2 m - 5 > 0 \end{cases} \Leftrightarrow \{\begin{cases} m^{2} - 8 m + 20 > 0 (l u ô n đ ú n g) \\ m > 0 \\ m > \frac{5}{2} \end{cases} \Leftrightarrow m > \frac{5}{2} K h i đ ó \{\begin{cases} 3^{x_{1}} = t_{1} \\ 3^{x_{2}} = t_{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = \log_{3} t_{1} \\ x_{2} = \log_{3} t_{2} \end{cases} Theo đề bài : x_{1} x_{2} < 0 \Rightarrow 0 < t_{1} < 1 < t_{2} \Leftrightarrow (t_{1} - 1) (t_{2} - 1) < 0 \Leftrightarrow t_{1} t_{2} - (t_{1} + t_{2}) + 1 < 0 Theo Vi - ét \{\begin{cases} t_{1} + t_{2} = m \\ t_{1} t_{2} = 2 m - 5 \end{cases} \Rightarrow 2 m - 5 - m + 1 < 0 \Leftrightarrow m < 4 Kết hợp ĐK ta có \frac{5}{2} < m < 4$

Câu 23:

Cho phương trình

$40 {(3 + 2 \sqrt{2})}^{x} + m {(3 - 2 \sqrt{2})}^{x}$ $+ m - 80 = 0$ (m là tham số). Có bao nhiêu giá trị nguyên của m để phương trình có hai nghiệm trái dấu?

A.19

B. vô số

C.1

D.20

Xem đáp án

Chọn A

Câu 24:

Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình $16^{x} - m . 4^{x - 1} + 5 m^{2} - 44 = 0$ có hai nghiệm đối nhau. Hỏi S có bao nhiêu phần tử?

A.2

B.0

C.1

D.3

Xem đáp án

Chọn B

$16^{x} - m . 4^{x - 1} + 5 m^{2} - 44 = 0 \Leftrightarrow {(4^{x})}^{2} - \frac{m}{4} . 4^{x} + 5 m^{2} - 44 = 0 (*) Đ ặ t 4^{x} = t (t > 0) P T (*) t r ở t h à n h t^{2} - \frac{m}{4} t + 5 m^{2} - 44 = 0 \Leftrightarrow 4 t^{2} - m t + 4 (5 m^{2} - 44) = 0 (1) P T (*) có 2 nghiệm phân biệt \Leftrightarrow PT (1) có 2 nghiệm dương phân biệt \Leftrightarrow \{\begin{array}{l} ∆ > 0 \\ S > 0 \\ P > 0 \end{array} \Leftrightarrow \{\begin{cases} m^{2} - 64 (5 m^{2} - 44) > 0 \\ \frac{m}{4} > 0 \\ 5 m^{2} - 44 > 0 \end{cases} \Leftrightarrow \{\begin{array}{l} - 319 m^{2} + 2816 > 0 \\ m > 0 \\ m^{2} > \frac{44}{5} \end{array} \Leftrightarrow \{\begin{cases} \frac{- 16}{\sqrt{29}} < m < \frac{16}{\sqrt{29}} \\ m > 0 \\ m \in (- \infty; \frac{- 2 \sqrt{55}}{5}) \cup (\frac{2 \sqrt{55}}{5}; + \infty) \end{cases} \Leftrightarrow \frac{2 \sqrt{55}}{5} < m < \frac{16}{\sqrt{29}} (2, 966 < m < 2, 971) Khi đó \{\begin{cases} 4^{x_{1}} = t_{1} \\ 4^{x_{2}} = t_{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = \log_{4} t_{1} \\ x_{2} = \log_{4} t_{2} \end{cases} PT có 2 nghiệm đối nhau \Leftrightarrow x_{1} + x_{2} = 0 \Leftrightarrow \log_{4} t_{1} + \log_{4} t_{2} = 0 \Leftrightarrow \log_{4} (t_{1} t_{2}) = 0 \Leftrightarrow \log_{4} (5 m^{2} - 44) = 0 \Leftrightarrow 5 m^{2} - 44 = 1 \Leftrightarrow m^{2} = 9 \Leftrightarrow m = \pm 3 (L) KL : Không có giá trị nào của m TM bài toán$

Câu 25:

Gọi S là tập hợp các giá trị thực của tham số m để phương trình $4^{x} - m . 2^{x} + 2 m + 1 = 0$ có nghiệm. Tập S có bao nhiêu giá trị nguyên?

A.1

B.4

C.9

D.7

Xem đáp án

Chọn C

Câu 26:

Cho phương trình $9^{x} - 2 (2 m + 1) 3^{x} + 3 (4 m - 1) = 0$ có hai nghiệm thực $x_{1}, x_{2}$ thỏa mãn $(x_{1} + 2) (x_{2} + 2) = 12$ . Giá trị của m thuộc khoảng

Xem đáp án

Câu 27:

Có bao nhiêu giá trị nguyên của m để phương trình $9^{x} - 8 . 3^{x} + m - 4 = 0$ có 2 nghiệm phân biệt?

A.16

B.15

C.14

D.13

Xem đáp án

$9^{x} - 8 . 3^{x} + m - 4 = 0 \Leftrightarrow {(3^{x})}^{2} - 8 . 3^{x} + m - 4 = 0 (*) Đặt 3^{x} = t (t > 0) PT (*) trở thành t^{2} - 8 t + m - 4 = 0 (1) PT (*) có 2 nghiệm phân biệt khi PT (1) có 2 nghiệm phân biệt dương \Rightarrow \{\begin{array}{l} ∆' > 0 \\ S > 0 \\ P > 0 \end{array} \Leftrightarrow \{\begin{cases} 16 - m + 4 > 0 \\ 8 > 0 \\ m - 4 > 0 \end{cases} \Leftrightarrow 4 < m < 20 Vậy có 15 giá trị nguyên của m thỏa mãn bài toán$

Câu 28:

Cho phương trình $(m - 5) . 3^{x} + (2 m - 2) . 2^{x} . \sqrt{3^{x}}$ $+ (1 - m) . 4^{x} = 0$ , tập hợp tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt là khoảng (a;b). Tính S=a+b

A.4

B.5

C.6

D.8

Xem đáp án

Chọn D

Câu 29:

Tìm tất cả các giá trị thực của tham số m để $4^{x} + 2^{x} + 4 = 3^{m} (2^{x} + 1)$ có hai nghiệm phân biệt.

Xem đáp án

Chọn C

Câu 30:

Tìm số giá trị nguyên của tham số $m \in (- 10; 10)$ để phương trình ${(\sqrt{10} + 1)}^{x^{2}} + m {(\sqrt{10} - 1)}^{x^{2}}$ $= 2 . 3^{x^{2} + 1}$ có đúng hai nghiệm phân biệt?

A.14

B.15

C.13

D.16

Xem đáp án

Chọn D

Câu 31:

Giả sử p, q là các số thực dương thỏa mãn $\log_{16} p = \log_{20} q$ $= \log_{25} (p + q)$ . Tìm giá trị của $\frac{p}{q}$

Xem đáp án

Câu 32:

Biết rằng phương trình $l o {g^{2}}_{3} x = l o g_{3} \frac{x^{4}}{3}$ có hai nghiệm a và b. Khi đó a.b bằng

A.8

B.81

C.9

D.64

Xem đáp án

Chọn B

Câu 33:

Phương trình $4^{x} + 1 = 2^{x} . m . c o s (π . x)$ có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là

A. Vô số

B. 1

C. 2

D. 0

Xem đáp án

Chọn B

Câu 34:

Phương trình ${(1 + \sqrt{2})}^{x} + (1 - 2 a) {(\sqrt{2} - 1)}^{x} - 4 = 0 (*)$ có 2 nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn $x_{1} - x_{2} = \log_{1 + \sqrt{2}} 3$ . Mệnh đề nào dưới đây đúng?

Xem đáp án

Chọn B

$Đặt {(1 + \sqrt{2})}^{x} = t \Rightarrow {(\sqrt{2} - 1)}^{x} = \frac{1}{t} \Rightarrow t + (1 - 2 a) \frac{1}{t} - 4 = 0 \Leftrightarrow t^{2} - 4 t + 1 - 2 a = 0 (1) PT (*) có 2 nghiệm phân biệt khi PT (1) có 2 nghiệm phân biệt dương \Leftrightarrow \{\begin{array}{l} ∆' > 0 \\ S > 0 \\ P > 0 \end{array} \Leftrightarrow \{\begin{array}{l} 4 + 2 a - 1 > 0 \\ 4 > 0 (luôn đúng) \\ 1 - 2 a > 0 \end{array} \Leftrightarrow \{\begin{cases} a > \frac{- 3}{2} \\ a < \frac{1}{2} \end{cases} \Leftrightarrow \frac{- 3}{2} < a < \frac{1}{2} khi đó \{\begin{cases} {(1 + \sqrt{2})}^{x_{1}} = t_{1} \\ {(1 + \sqrt{2})}^{x_{2}} = t_{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = \log_{1 + \sqrt{2}} t_{1} \\ x_{2} = \log_{1 + \sqrt{2}} t_{2} \end{cases} Theo ĐB : x_{1} - x_{2} = \log_{1 + \sqrt{2}} 3 \Leftrightarrow \log_{1 + \sqrt{2}} t_{1} - \log_{1 + \sqrt{2}} t_{2} = \log_{1 + \sqrt{2}} 3 \Leftrightarrow \frac{t_{1}}{t_{2}} = 3 \Leftrightarrow t_{1} = 3 t_{2} Theo Vi - ét : \{\begin{cases} t_{1} + t_{2} = 4 \\ t_{1} t_{2} = 1 - 2 a \end{cases} . Thay t_{1} = 3 t_{2} ta tìm được \{\begin{cases} t_{1} = 3 \\ t_{2} = 1 \end{cases} \Rightarrow 1 - 2 a = 3 \Leftrightarrow a = - 1 \in (\frac{- 3}{2}; 0) (T M Đ K)$

Câu 35:

Trên đoạn [0;2019] có bao nhiêu số nguyên m để phương trình $9^{x} - 2 (m + 2) . 3^{x}$ $+ 3 m - 2 = 0$ (*)có hai nghiệm trái dấu?

A.2010

B.2019

C.5

D.4

Xem đáp án

Chọn D

$Đặt 3^{x} = t . PT (*) trở thành t^{2} - 2 (m + 2) t + 3 m - 2 = 0 (1) PT (*) có 2 nghiệm phân biệt khi PT (1) có 2 nghiệm dương phân biệt \Leftrightarrow \{\begin{array}{l} ∆' > 0 \\ S > 0 \\ P > 0 \end{array} \Leftrightarrow \{\begin{cases} {(m + 2)}^{2} + 2 - 3 m > 0 \\ 2 (m + 2) > 0 \\ 3 m - 2 > 0 \end{cases} \Leftrightarrow \{\begin{array}{l} m^{2} + m + 6 > 0 (luôn đúng) \\ m > - 2 \\ m > \frac{2}{3} \end{array} \Leftrightarrow m > \frac{2}{3} Khi đó \{\begin{cases} 3^{x_{1}} = t_{1} \\ 3^{x_{2}} = t_{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = \log_{3} t_{1} \\ x_{2} = \log_{3} t_{2} \end{cases} Từ ĐB \Rightarrow x_{1} x_{2} < 0 \Rightarrow 0 < t_{1} < 1 < t_{2} \Leftrightarrow (t_{1} - 1) (t_{2} - 1) < 0 \Leftrightarrow t_{1} t_{2} - (t_{1} + t_{2}) + 1 < 0 . Theo Vi - ét \{\begin{cases} t_{1} + t_{2} = 2 (m + 2) \\ t_{1} t_{2} = 3 m - 2 \end{cases} \Rightarrow 3 m - 2 - 2 (m + 2) + 1 < 0 \Leftrightarrow m - 5 < 0 \Leftrightarrow m < 5 mà m \in [0; 2019] \Rightarrow 0 \leq m < 5 Vậy có 5 giá trị nguyên của m thỏa mãn bài toán$

Câu 36:

Tìm tất cả các giá trị của tham số m để phương trình $4 {(\log_{2} \sqrt{x})}^{2} - \log_{\frac{1}{2}} x + m = 0$ có nghiệm thuộc khoảng $(0; 1)$

Xem đáp án

Chọn D

Câu 37:

Số giá trị nguyên của m thuộc đoạn [-2019;2019] để $4^{x} - (m + 3) 2^{x} + 3 m + 1 = 0$ có đúng một nghiệm lớn hơn 0 là

A.2021

B.2022

C.2019

D.2020

Xem đáp án

Chọn B

$t^{2} - (m + 3) t + 3 m + 1 = 0 \Leftrightarrow t^{2} - 3 t + 1 = m t - 3 m$

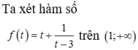
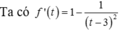
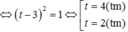
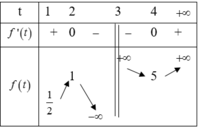
Câu 38:

Cho phương trình $l o {g^{2}}_{3} x - 4 l o g_{3} x + m - 3 = 0$ . Có bao nhiêu giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt $x_{1} < x_{2}$ thỏa mãn $x_{2} - 81 x_{1} < 0$

A.4

B.5

C.3

D.6

Xem đáp án

Chọn C

Câu 39:

Cho phương trình $l o {g^{2}}_{3} x - 4 l o g_{3} x + m - 3 = 0$ . Có bao nhiêu giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt $x_{1} < x_{2}$ thỏa mãn $x_{2} - 81 x_{1} < 0$

A.4

B.5

C.3

D.6

Xem đáp án

Chọn C

Câu 40:

Cho phương trình $4^{x + 1} - (8 m + 5) . 2^{x} + 2 m + 1 = 0$ (m là tham số) có hai nghiệm phân biệt $x_{1}, x_{2}$ , thỏa mãn $x_{1} . x_{2} = - 1$ . Khẳng định nào sau đây là đúng?

Xem đáp án

Chọn D

CHỌN BỘ SÁCH BẠN MUỐN XEM

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P4)

Danh sách câu hỏi

Bài thi liên quan