30 câu hỏi trắc nghiệm thuộc Bài tập số phức mức độ cơ bản, nâng cao cực hay có lời giải chi tiết(P2) - qa.haylamdo.com

Bài tập số phức mức độ cơ bản, nâng cao cực hay có lời giải chi tiết

Bài tập số phức mức độ cơ bản, nâng cao cực hay có lời giải chi tiết(P2)

3302 lượt thi
30 câu hỏi
50 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Biết z thỏa mãn $| \bar{z} - 1 + i | = | z + 3 + i |$ . Tìm ${|z|}_{m i n}$

A. ${|z|}_{m i n}$ = $\frac{2}{\sqrt{5}}$

B. ${|z|}_{m i n}$ = $\frac{1}{\sqrt{5}}$

C. ${|z|}_{m i n}$ = 1

D. ${|z|}_{m i n}$ = 3

Đáp án A

$Đặt z = a + bi (a; b \in ℝ) \Rightarrow \bar{z} = a - bi |\bar{z} - 1 + i| = |a - 1 + (1 - b) i| = \sqrt{{(a - 1)}^{2} + {(1 - b)}^{2}} |z + 3 + i| = |a + 3 + (b + 1) i| = \sqrt{{(a + 3)}^{2} + {(b + 1)}^{2}} Từ giả thiết đề bài \Rightarrow {(a - 1)}^{2} + {(1 - b)}^{2} = {(a + 3)}^{2} + {(b + 1)}^{2} \Leftrightarrow - 2 a + 1 + 1 - 2 b = 6 a + 9 + 2 b + 1 \Leftrightarrow 8 a + 4 b + 8 = 0 \Leftrightarrow 2 a + b + 2 = 0 \Leftrightarrow b = - 2 - 2 a \Rightarrow |z| = \sqrt{a^{2} + {(- 2 - 2 a)}^{2}} = \sqrt{a^{2} + 4 + 8 a + 4 a^{2}} = \sqrt{5 a^{2} + 8 a + 4} Đặt f (x) = 5 a^{2} + 8 a + 4 f' (x) = 10 a + 8 = 0 \Leftrightarrow a = \frac{- 4}{5} \Rightarrow f {(x)}_{\min} = f (\frac{- 4}{5}) = \frac{4}{5} \Rightarrow {|z|}_{\min} = \sqrt{\frac{4}{5}} = \frac{2}{\sqrt{5}}$

Câu 2:

Biết số phức $z \neq$ 0 và w = $\frac{z}{1 - i}$ . Biết A,B là các điểm biểu diễn của z,w thì:

A. $∆$ ABO đều

B. $∆$ ABO vuông cân

C. O là trung điểm AB

D. $∆$ ABO có một góc $30^{0}$

Đáp án B

$Đặt z = a + bi (a; b \in ℝ) \Rightarrow điểm biểu diễn số phức z là A (a; b) \Rightarrow w = \frac{z}{1 - i} = \frac{z (1 + i)}{1 - i^{2}} = \frac{(a + bi) (1 + i)}{2} = \frac{a - b + (a + b) i}{2} \Rightarrow Điểm biểu diễn số phức w là B (\frac{a - b}{2}; \frac{a + b}{2}) Ta có : \vec{AB} = (\frac{- a - b}{2}; \frac{a - b}{2}) \Rightarrow AB = \sqrt{\frac{{(a + b)}^{2}}{4} + \frac{{(a - b)}^{2}}{4}} \vec{OA} = (a; b) \Rightarrow OA = \sqrt{a^{2} + b^{2}} \vec{OB} = (\frac{a - b}{2}; \frac{a + b}{2}) \Rightarrow OB = \sqrt{\frac{{(a - b)}^{2}}{4} + \frac{{(a + b)}^{2}}{4}} \Rightarrow △ ABO cân tại B (1) Mặt khác : \vec{AB} . \vec{BO} = \frac{- a - b}{2} . \frac{- (a - b)}{2} + \frac{a - b}{2} . \frac{- (a + b)}{2} = \frac{a^{2} - b^{2}}{4} - \frac{a^{2} - b^{2}}{4} = 0 \Rightarrow △ ABO vuông tại B (2) Từ (1) và (2) \Rightarrow △ ABO vuông cân tại B$

Câu 3:

Tìm phần ảo của số phức z = $\frac{z - 4 i}{i^{3}}$ . Phần ảo của z bằng?

A. 2i

B. 2

C. $\sqrt{13}$

D. -3

Đáp án B

$z = \frac{z - 4 i}{i^{3}} \Leftrightarrow - zi = z - 4 i \Leftrightarrow - zi - z = - 4 i \Leftrightarrow z (- i - 1) = - 4 i \Leftrightarrow z = \frac{- 4 i}{- i - 1} = \frac{4 i (i - 1)}{i^{2} - 1} = \frac{- 4 - 4 i}{- 2} = 2 + 2 i \Rightarrow Phần thực của số phức z là 2$

Câu 4:

Biết z không phải là số phức thuần ảo và M, N là biểu diễn của z và $w = - \bar{z}$ thì:

A. M, N đối xứng qua O

B. M trùng N

C. M, N đối xứng nhau qua Ox

D. M, N đối xứng nhau qua Oy

Đáp án D

$Gọi M (a; b) là điểm biểu diễn số phức z = a + bi \Rightarrow w = - \bar{z} = - (a - bi) = - a + bi \Rightarrow Điểm biểu diễn số phức w là N (- a; b) Ta thấy tung độ 2 điểm M và N bằng nhau vào hoành độ 2 điểm này đối nhau \Rightarrow M và N đối xứng nhau qua trục Oy$

Câu 5:

Số phức z nào dưới đây là nghiệm của phương trình: $(- 1 + i) z^{4} - 3 (2 - i) z^{2} + (16 i + 2) = 0$

A. z = i

B. z = -i

C. z = i + 1

D. z = 5

Đáp án C

Thay từng các đáp án, nếu thấy 2 vế của phương trình bằng nhau thì đáp án đó là nghiệm của phương trình

Câu 6:

Biết $z_{1}, z_{2}$ là 2 nghiệm của phương trình: $3 z^{2} - 4 z + 2 = 0$ . Tính S = $z_{1} {(\bar{z_{2}})}^{2} + {(\bar{z_{1}})}^{2} z_{2}$

A. S = $- \frac{8}{27}$

B. S = $\frac{8}{27}$

C. S = $\frac{8 (1 - i)}{27}$

D. S = $\frac{27 (1 + i)}{8}$

Đáp án A

$Giải PT : 3 z^{2} - 4 z + 2 = 0 \Leftrightarrow \{\begin{cases} z_{1} = \frac{2}{3} + \frac{\sqrt{2}}{3} i \\ z_{2} = \frac{2}{3} - \frac{\sqrt{2}}{3} i \end{cases} \Rightarrow S = z_{1} {(\bar{z_{2}})}^{2} + z_{2} {(\bar{z_{1}})}^{2} = (\frac{2}{3} + \frac{\sqrt{2}}{3} i) {(\frac{2}{3} + \frac{\sqrt{2}}{3} i)}^{2} + (\frac{2}{3} - \frac{\sqrt{2}}{3} i) {(\frac{2}{3} - \frac{\sqrt{2}}{3} i)}^{2} = {(\frac{2}{3} + \frac{\sqrt{2}}{3} i)}^{3} + {(\frac{2}{3} - \frac{\sqrt{2}}{3} i)}^{3} = \frac{- 8}{27}$

Câu 7:

Biết tập hợp điểm biểu diễn z là đường thẳng d, tập hợp biểu diễn w (với $w = \frac{z}{i}$ ) là $∆$ thì:

A. ( $∆$ ) $\equiv$ (d)

B. ( $∆$ )//(d)

C. ( $∆$ ) $⊥$ (d)

D. ( $∆$ ) không phải là đường thẳng

Đáp án C

$Đặt z = a + bi (a; b \in ℝ) \Leftrightarrow điểm biểu diễn z là M (a; b) \Rightarrow w = \frac{z}{i} = \frac{zi}{i^{2}} = \frac{(a + bi) i}{- 1} = \frac{- b + ai}{- 1} = b - ai \Rightarrow điểm biểu diễn z là N (b; - a) Giả sử d và ∆ đi qua gốc tọa độ thì PTĐT d có VTCP là \vec{OM} = (a; b) PTĐT ∆ có VTCP là \vec{ON} = (b; - a) \Rightarrow \vec{OM} . \vec{ON} = ab - ab = 0 \Rightarrow \vec{OM} ⊥ \vec{ON} \Rightarrow d ⊥ ∆$

Câu 8:

Tìm ${|z|}_{m a x}$ biết z thay đổi luôn thỏa mãn |z-1+3i| = 2

A. ${|z|}_{m a x}$ = 3 + $\sqrt{5}$

B. ${|z|}_{m a x}$ = 2 + $\sqrt{10}$

C. ${|z|}_{m a x}$ = 1 + $\sqrt{13}$

D. ${|z|}_{m a x}$ = 6

Đáp án B

$Đặt z = x + yi (x; y \in ℝ) Theo ĐB : |z - 1 + 3 i| = |x - 1 + (y - 3) i| = \sqrt{{(x - 1)}^{2} + {(y - 3)}^{2}} = 2 \Rightarrow {(x - 1)}^{2} + {(y - 3)}^{2} = 4 Tập hợp các điểm biểu diễn z nằm trên đường tròn tâm I (1; 3) và R = 2$

Từ hình vẽ suy ra: ${|z|}_{m a x} = O I + R = \sqrt{10} + 2$

Câu 9:

Biết M(2;-1) là điểm biểu diễn số phức $\bar{Z}$ . Tìm Z.

A. Z = 2 + i

B. Z = 1 - i

C. Z = 1 + i

D. Z = 1 + 2i

Đáp án A

M(2;-1) là điểm biểu diễn số phức $\bar{z}$

$\Rightarrow \bar{z} = 2 - i \Rightarrow z = 2 + i$

Câu 10:

Tìm số phức Z, biết Z là nghiệm của phương trình: $(2 i - 1) Z^{2} - 2 i \bar{Z} + (6 + 4 i) = 0$

A. Z = -i

B. Z = 1-i

C. Z = 1+i

D. Z = i

Đáp án C

Thay từng các đáp án, nếu thấy 2 vế của phương trình bằng nhau thì đáp án đó là nghiệm của phương trình

Câu 11:

$\Leftrightarrow$ Cho số phức Z₁, Z₂ với Z₁ $= a_{1} + b_{1} i$ , Z₂ $= a_{2} + b_{2} i (a_{1}, b_{1}, a_{2}, b_{2} \in ℝ)$ . Chọn phát biểu đúng:

A. Z₁= Z₂ $\Leftrightarrow$ |Z₁| = |Z₂|

B. Z₁ $\neq$ Z₂ thì $b_{1} \neq b_{2}$

C. Z₁= Z₂ $\Leftrightarrow$ $a_{1} = a_{2}$

D. $Z_{1} = \bar{Z_{2}} \Leftrightarrow Z_{2} = \bar{Z_{1}}$

Đáp án D

$z_{1} = z_{2} \Leftrightarrow \{\begin{cases} a_{1} = a_{2} \\ b_{1} = b_{2} \end{cases} n h ư n g |z_{1}| = |z_{2}| \Leftrightarrow a_{1}^{2} + b_{1}^{2} = a_{2}^{2} + b_{2}^{2} z_{1} = \bar{z_{2}} \Leftrightarrow \{\begin{cases} a_{1} = a_{2} \\ b_{1} = - b_{2} \end{cases} \Leftrightarrow \{\begin{cases} a_{1} = a_{2} \\ - b_{1} = b_{2} \end{cases} \Leftrightarrow z_{2} = \bar{z_{1}}$

Câu 12:

Có bao nhiêu số phức Z thỏa mãn $\{\begin{cases} | Z + 2 i - 1 | = | i | \\ | Z + 3 - i | = 4 \end{cases}$

A. Không có.

B. Có 1 số.

C. Có 2 số.

D. Có vô số.

Đáp án B

$Đ ặ t z = a + b i (a; b \in ℝ) . Ta có : |z + 2 i - 1| = |i| \Leftrightarrow \sqrt{{(a - 1)}^{2} + {(b + 2)}^{2}} = 1 \Leftrightarrow {(a - 1)}^{2} + {(b + 2)}^{2} = 1 \Leftrightarrow a^{2} + b^{2} - 2 a + 4 b + 1 + 4 = 1 \Leftrightarrow a^{2} + b^{2} = 2 a - 4 b - 4 (1) Và |z + 3 - i| = 4 \Leftrightarrow {(a + 3)}^{2} + {(b - 1)}^{2} = 16 \Leftrightarrow a^{2} + b^{2} + 6 a - 2 b + 9 + 1 = 16 \Leftrightarrow a^{2} + b^{2} = - 6 a + 2 b + 6 (2) Từ (1) và (2) \Rightarrow 2 a - 4 b - 4 = - 6 a + 2 b + 6 \Leftrightarrow 8 a - 6 b = 10 \Leftrightarrow a = \frac{10 + 6 b}{8} = \frac{5 + 3 b}{4} . Thay vào (1) {(\frac{5 + 3 b}{4})}^{2} + b^{2} = 2 . \frac{5 + 3 b}{4} - 4 b - 4 \Leftrightarrow {(5 + 3 b)}^{2} + 16 b^{2} = 8 (5 b + 3) - 64 b - 64 \Leftrightarrow b = \frac{- 7}{5} \Rightarrow a = \frac{1}{5} KL : Có 1 số phức thỏa mãn bài toán$

Câu 13:

Biết tập hợp điểm M biểu diễn số phức Z là (d): x-y-2 = 0. Đặt W = Z+1-i. Tìm ${|W|}_{m i n}$

A. ${|W|}_{m i n}$ = $\sqrt{2}$

B. ${|W|}_{m i n}$ = 2

C. ${|W|}_{m i n}$ = 2 $\sqrt{2}$

D. ${|W|}_{m i n}$ = 4

Đáp án C

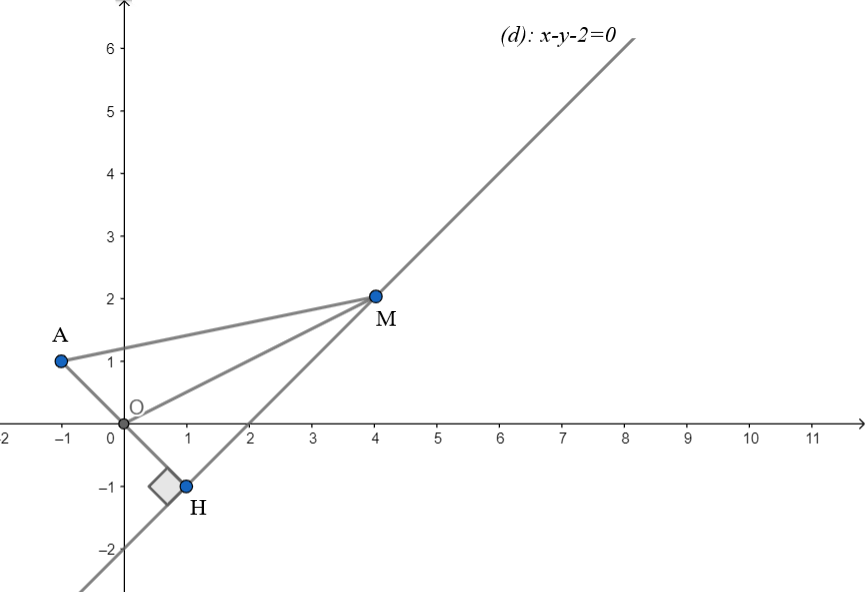
Gọi A (-1;1); O(0;0); và M(a;b) thuộc tập hợp các điểm thuộc (d) biểu diễn số phức z

$\Rightarrow \vec{AM} = (a + 1; b - 1) biêu diễn số phức w = z + 1 - i \Rightarrow |w| = AM Nhận xét : Để {AM}_{\min} thì {OM}_{\min} do OA cố định Từ hình vẽ ta thấy {OM}_{\min} \Leftrightarrow OM ⊥ d hay OM \equiv OH Mặt khác OH = d (O; d) = \frac{|- 2|}{\sqrt{1^{2} + 1^{2}}} = \sqrt{2} Từ hình vẽ ta thấy 3 điểm A; O; H thẳng hàng \Rightarrow {AM}_{\min} = AH = OH + OA = \sqrt{2} + \sqrt{2} = 2 \sqrt{2}$

Câu 14:

Cho z, w là 2 số phức được biểu diễn bởi hai điểm đối xứng nhau qua trục Oy. Biết z = 1 + 2i. Tìm w

A. w = 1-2i

B. w = -1+2i

C. w = 2 + i

D. w = 2 - i

Đáp án B

$Đặt w = a + bi (a; b \in ℝ) . Ta có z = 1 + 2 i Mặt khác z, w là 2 số phức được biểu diễn bởi hai điểm đối xứng nhau qua trục Oy \Rightarrow \{\begin{array}{l} a = - 1 \\ b = 2 \end{array} \Rightarrow w = - 1 + 2 i$

Câu 15:

Gọi S là tổng các nghiệm phức của phương trình ${(z - 1)}^{4}$ = 5. Tính S.

A. S = 0

B. S = 4

C. S = 2i

D. S = $4 \sqrt{5}$

Đáp án B

${(z - 1)}^{4} = 5 \Leftrightarrow \{\begin{cases} {(z - 1)}^{2} = \sqrt{5} \\ {(z - 1)}^{2} = - \sqrt{5} \end{cases} \Rightarrow \{\begin{cases} z^{2} - 2 z + 1 - \sqrt{5} = 0 (1) \\ z^{2} - 2 z + 1 + \sqrt{5} = 0 (2) \end{cases} Gọi z_{1}; z_{2} là nghiệm phức của (1) \Rightarrow z_{1} + z_{2} = 2 Và z_{3}; z_{4} là nghiệm phức của (2) \Rightarrow z_{3} + z_{4} = 2 \Rightarrow S = z_{1} + z_{2} + z_{3} + z_{4} = 2 + 2 = 4$

Câu 16:

Cho số phức z và w biết w = $\frac{z}{1 - i}$ và M, N lần lượt là các điểm biểu diễn z, w trong Oxy. Biết diện tích $∆$ OMN bằng 1. Tính |z|.

A. |z| = $\frac{1}{2}$

B. |z| = 1

C. |z| = $\sqrt{2}$

D. |z| = 2

Đáp án D

$Đặt z = x + yi (x; y \in ℝ) \Rightarrow w = \frac{z}{1 - i} = \frac{z (1 + i)}{1 - i^{2}} = \frac{(x + yi) (1 + i)}{2} = \frac{x - y + (x + y) i}{2} Gọi M (x; y) là điểm biểu diễn số phức z và N (\frac{x - y}{2}; \frac{x + y}{2}) là điểm biểu diễn số phức w Ta có : \vec{OM} = (x; y) và \vec{ON} = (\frac{x - y}{2}; \frac{x + y}{2}) S_{∆ OMN} = \frac{1}{2} |\begin{matrix} x & \frac{x - y}{2} \\ y & \frac{x + y}{2} \end{matrix}| = \frac{1}{2} (x . \frac{x + y}{2} - y . \frac{x - y}{2}) = 1 \Leftrightarrow \frac{x^{2} + xy}{2} - \frac{xy - y^{2}}{2} = 2 \Leftrightarrow x^{2} + y^{2} = 4 \Leftrightarrow \sqrt{x^{2} + y^{2}} = 2 \Leftrightarrow |z| = 2$

Câu 17:

Cho z = $\frac{1 - 2 i}{4 + 3 i}$ thì số phức liên hợp $\bar{z}$ bằng :

A. $\bar{z}$ = $\frac{1 + 2 i}{4 + 3 i}$

B. $\bar{z}$ = $\frac{4 + 3 i}{1 - 2 i}$

C. $\bar{z}$ = $\frac{1 + 2 i}{4 - 3 i}$

D. $\bar{z}$ = $\frac{4 - 3 i}{1 + 2 i}$

Đáp án C

$z = \frac{1 - 2 i}{4 + 3 i} = \frac{- 2}{25} - \frac{11}{25} i \Rightarrow \bar{z} = \frac{- 2}{25} + \frac{11}{25} i Trong 4 đáp án ta thấy đáp án C : \frac{1 + 2 i}{4 - 3 i} = \frac{- 2}{25} + \frac{11}{25} i$

Câu 18:

Biết z₁, z₂ là các nghiệm phức của phương trình $2 z^{2} - 5 z + 4 = 0$ Tính tổng S = $z_{1}^{2} . \bar{z_{2}} + z_{2}^{2} . \bar{z_{1}}$

$A . S = \frac{5}{8}$

$B . S = \frac{27}{8}$

$C . S = \frac{25 - 2 i \sqrt{7}}{8}$

$D . S = 1$

Đáp án A

$Giải PT : 2 z^{2} - 5 z + 4 = 0 \Leftrightarrow \{\begin{cases} z_{1} = \frac{5}{4} + \frac{\sqrt{7}}{4} \\ z_{2} = \frac{5}{4} - \frac{\sqrt{7}}{4} \end{cases} Ta thấy z_{1} và z_{2} là 2 số phức liên hợp của nhau \Rightarrow S = z_{1}^{2} . \bar{z_{2}} + z_{2}^{2} . \bar{z_{1}} = z_{1}^{3} + z_{2}^{3} = (z_{1} + z_{2}) [{(z_{1} + z_{2})}^{2} - 3 z_{1} z_{2}] Áp dụng định lý Vi - ét : \{\begin{cases} z_{1} + z_{2} = \frac{5}{2} \\ z_{1} z_{2} = 2 \end{cases} \Rightarrow S = \frac{5}{2} [{(\frac{5}{2})}^{2} - 3.2] = \frac{5}{8}$

Câu 19:

Có bao nhiêu số phức z thỏa mãn |z-1-2i| = 2 sao cho z $\in ℝ$ hoặc iz $\in ℝ$ ?

A. Có 1 số

B. Có 3 số.

C. Có 4 số.

D. Có vô số số.

Đáp án B

$Đặt z = a + bi (a; b \in ℝ) z \in ℝ \Leftrightarrow b = 0 Ta có : |z - 1 - 2 i| = |a - 1 + (b - 2) i| = \sqrt{{(a - 1)}^{2} + {(b - 2)}^{2}} = 2 (*) Mặt khác : iz = i (a + bi) = - b + ai \in ℝ \Leftrightarrow a = 0 TH 1 : a = 0 thì (*) \Leftrightarrow \sqrt{1 + {(b - 2)}^{2}} = 2 \Leftrightarrow 1 + {(b - 2)}^{2} = 4 \Leftrightarrow b = 2 + \sqrt{3} hoặc b = 2 - \sqrt{3} TH 2 : b = 0 thì (*) \Leftrightarrow \sqrt{{(a - 1)}^{2} + 4} = 2 \Leftrightarrow {(a - 1)}^{2} + 4 = 4 \Leftrightarrow a = 1$

KL: Có 3 số phức z thỏa mãn bài toán

Câu 20:

Xét các số phức thỏa mãn : |z-2i| = |z-4+i| Tìm ${|z|}_{m i n}$ .

A. ${|z|}_{m i n}$ = $\frac{1}{2}$

B. ${|z|}_{m i n}$ = 1

C. ${|z|}_{m i n}$ = $\frac{13}{10}$

D. ${|z|}_{m i n}$ = $\frac{3}{2}$

Đáp án C

$Đặt z = x + yi (x; y \in ℝ) Từ ĐB \Rightarrow |x + (y - 2) i| = |x - 4 + (y + 1) i| \Leftrightarrow x^{2} + {(y - 2)}^{2} = {(x - 4)}^{2} + {(y + 1)}^{2} \Leftrightarrow - 4 y + 4 = - 8 x + 16 + 2 y + 1 \Leftrightarrow 8 x - 6 y - 13 = 0 (d) Gọi M (x; y) \in (d) thì |z| = OM {|z|}_{\min} \Leftrightarrow {OM}_{\min}$

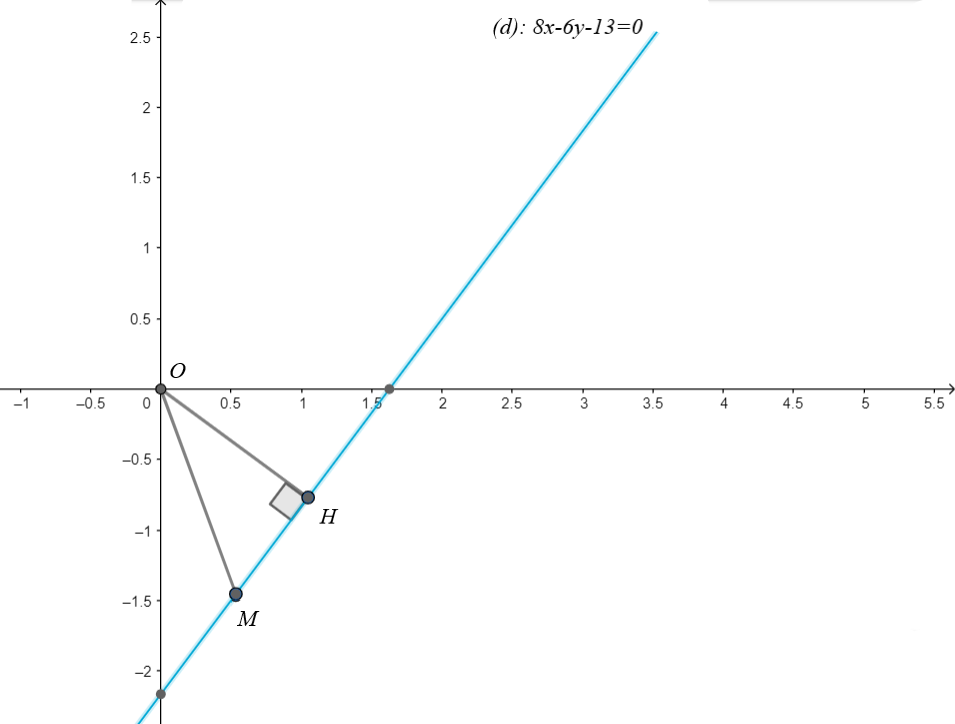
Từ hình vẽ ta thấy OM_min khi

$OM ⊥ d hay OM \equiv OH Mặt khác OH = d (O; d) = \frac{|- 13|}{\sqrt{8^{2} + 6^{2}}} = \frac{13}{10} \Rightarrow {|z|}_{\min} = OH = \frac{13}{10}$

Câu 21:

Biết $Z_{1}, Z_{2}$ là hai số phức khác 0 và $Z_{1} = \bar{Z_{2}}$ . Gọi $M_{1}, M_{2}$ là biểu diễn hình học của $Z_{1}, Z_{2}$ . Chọn khẳng định đúng.

A. $M_{1}, M_{2}$ luôn đối xứng qua O

B. $M_{1}, M_{2}$ đối xứng qua Ox

C. $M_{1}, M_{2}$ đối xứng qua Oy

D. Cả A,B,C đều sai.

Đáp án B

$Đặt z_{1} = a + bi và z_{2} = c + di (a; b; c; d \in ℝ) \Rightarrow M_{1} (a; b) biểu diễn số phức z_{1} và M_{2} (c; d) bểu diễn số phức z_{2} \Rightarrow \bar{z_{2}} = c - di Mà z_{1} = \bar{z_{2}} \Leftrightarrow \{\begin{cases} a = c \\ b = - d \end{cases} \Rightarrow M_{1} và M_{2} đối xứng nhau qua trục Ox$

Câu 22:

Số phức z nào dưới đây không phải nghiệm phương trình ${(z - 2)}^{4}$ = 16?

A. z = 0

B. z = 2-2i

C. z = 2+2i

D. z = -2-2i

Đáp án D

Thay từng đáp án vào PT:

$Với z = 0 thì PT trở thành {(0 - 2)}^{4} = 2^{4} = 16 (đúng) \Rightarrow z = 0 là nghiệm của PT Với z = 2 - 2 i thì PT trở thành : {(2 - 2 i - 2)}^{4} = (- 2 i)^{4} = 16 . i^{4} = 16 (đúng) \Rightarrow z = 2 - 2 i là nghiệm của PT Với z = 2 + 2 i thì PT trở thành : {(2 + 2 i - 2)}^{4} = (2 i)^{4} = 16 . i^{4} = 16 (đúng) \Rightarrow z = 2 + 2 i là nghiệm của PT Với z = - 2 - 2 i thì PT trở thành : {(- 2 - 2 i - 2)}^{4} = (- 4 - 2 i)^{4} \neq 16 (sai) \Rightarrow z = - 2 - 2 i không là nghiệm của PT$

Câu 23:

Đặt $z = {(\frac{1 + i}{\sqrt{2}})}^{2 n}$ với $n \in {1, 2, 3, . . . ., 20}$ thì:

$A . z \in {\pm i}$

$B . z \in {\pm 2}$

$C . z \in {\pm 1, \pm i}$

$D . z \in {\pm 4, \pm i, 0}$

Đáp án C

$z = {(\frac{1 + i}{\sqrt{2}})}^{2 n} = {[{(\frac{1 + i}{\sqrt{2}})}^{2}]}^{n} = {(\frac{2 i}{2})}^{n} = i^{n} Với : n = 1 thì z = i n = 2 thì z = i^{2} = - 1 n = 3 thì z = i^{3} = - i n = 4 thì z = i^{4} = 1 NX : i^{2 n + 2} = i^{2} . {(i^{2})}^{n} = (- 1) . {(- 1)}^{n} = {(- 1)}^{n + 1} v à i^{2 n + 1} = i . i^{2 n} = i . {(- 1)}^{n} KL : Với n \in \{1; 2; . . .; 20\} thì z \in \{\pm 1; \pm i\}$

Câu 24:

Số phức z nào dưới đây là nghiệm phương trình (1+i) $z^{2} - (2 - i) \bar{z} + i - 2 = 0 ?$

A. z = 4

B. z = 1 + i

C. z = -2i

D. z = 2 - i

Đáp án D

Thay từng các đáp án, nếu thấy 2 vế của phương trình bằng nhau thì đáp án đó là nghiệm của phương trình

Câu 25:

Tìm a để phương trình $3 (\sqrt{3} z^{3} - 3 i z^{2} - \sqrt{3} z + 1) = a$ có nghiệm duy nhất.

A. a = 3 + i

B. a = 1 + i $\sqrt{3}$

C. a = 3 - i

D. Không tồn tại a

Đáp án C

Câu 26:

Biết các số phức z thỏa mãn : |z+1| + |z-1| = 4. Tìm Min |z|

A. ${|z|}_{m i n} = \sqrt{3}$

B. ${|z|}_{m i n} = 1$

C. ${|z|}_{m i n} = \sqrt{2} - 1$

D. ${|z|}_{m i n} = 2$

Đáp án A

Ta thấy quỹ tích điểm biểu diễn số phức z là Elip có độ dài trục lớn là 2a = 4, tiêu cự là 2c = 2

$\Rightarrow b = \sqrt{a^{2} - c^{2}} = \sqrt{2^{2} - 1^{2}} = \sqrt{3} \Rightarrow \min |z| = \sqrt{3}$

Câu 27:

Số phức $z \neq 0$ thuần ảo được biểu diễn bởi điểm M. Có bao nhiêu phát biểu dưới đây là đúng?

* M $\notin$ trục Ox

* M $\notin$ trục Oy

* M $\notin$ đường thẳng x = 1

* M $\notin$ đường thẳng y = 1

A. 4 phát biểu đúng

B. 3 phát biểu đúng

C. 2 phát biểu đúng

D. 1 phát biểu đúng

E. Không có phát biểu nào

Đáp án B

$D o z l à s ố t h u ầ n ả o v à k h á c 0 \Rightarrow Đ ặ t z = a i (a \neq 0) \Rightarrow M (0; a) b i ể u d i ễ n s ố p h ứ c z \Rightarrow Đ i ể m M n ằ m t r ê n t r ụ c t u n g$

Câu 28:

Tìm số phức liên hợp của z = $(2 + \sqrt{3}) + (2 - \sqrt{3}) i$

$A . \bar{z} = (2 + \sqrt{3}) - i (2 + \sqrt{3})$

$B . \bar{z} = (\sqrt{3} + 2) + i (\sqrt{3} - 2)$

$C . \bar{z} = (2 - \sqrt{3}) - i (2 + \sqrt{3})$

$D . \bar{z} = (2 - \sqrt{3}) - (2 + \sqrt{3}) i$

Đáp án B

$z = (2 + \sqrt{3}) + (2 - \sqrt{3}) i \Rightarrow \bar{z} = (2 + \sqrt{3}) - (2 - \sqrt{3}) i = (2 + \sqrt{3}) + (\sqrt{3} - 2) i$

Câu 29:

Cho z = 3(1 + i) - 4(1-i). Tìm |z|

A. |z| = $5 \sqrt{2}$

B. |z| = 5

C. |z| = 7

D. |z| = 50

Đáp án A

$z = 3 (1 + i) - 4 (1 - i) = 3 + 3 i - 4 + 4 i = - 1 + 7 i \Rightarrow |z| = \sqrt{{(- 1)}^{2} + 7^{2}} = \sqrt{50} = 5 \sqrt{2}$

Câu 30:

Số phức z nào dưới đây là nghiệm phương trình (1-i) $z^{4} - 3 i \bar{z} + 7 - i = 0 ?$

A. z = i

B. z = $2 + \sqrt{3}$

C. z = 1-i

D. z = 1+i

Đáp án D

Thay từng các đáp án, nếu thấy 2 vế của phương trình bằng nhau thì đáp án đó là nghiệm của phương trình

Bắt đầu thi ngay

Bài thi liên quan