Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) (Đề 8)
-
1552 lượt thi
-
42 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 2:
Chọn D.
Rõ ràng đồ thị hàm số nhận đường thẳng x = -1 là tiệm cận đứng.Câu 3:
![Cho hàm số y = f(x) xác định, liên tục trên đoạn [-2;2] và có đồ thị là đường cong (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/06/blobid0-1656424923.png)
Chọn B.
Từ hình vẽ ta có ngay hàm số f(x) đạt cực đại tại điểm x = -1Câu 4:
Cho hàm số . Hàm số có:
Chọn D.
Tập xác định .
Đạo hàm: với ⇒ Hàm số không có cực trị.
Nhận xét rằng hàm phân thức bậc nhất trên bậc nhất không có cực trị nên ta thấy ngay việc lựa chọn đáp án D là đúngCâu 5:
Chọn A.
Với các số thực dương a,b bất kì ta có vàCâu 6:
Chọn B.
Biến đổi hoặc sử dụng MTCT thử các kết quả bằng phím CALC
Câu 8:
Cho hàm số xác định và liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định SAI?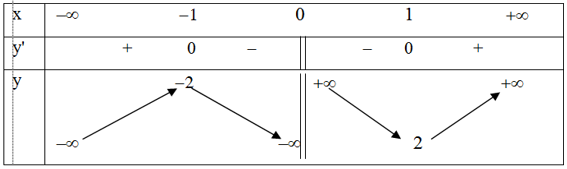
Chọn C.
Khẳng định C sai vì hàm số có giá trị cực đại bằng -2 và giá trị cực tiểu bằng 2.
Câu 9:
Chọn A.
Tập xác định .
Đạo hàm: , .
Khi đó, tích các giá trị cực đại và cực tiểu của hàm số bằng:
.Câu 10:
Chọn D.
TXĐ: .
Ta có: suy ra đường thẳng y = -2 là TCN của đồ thị hàm số.
suy ra đường thẳng y = 2 là TCN của đồ thị hàm số.
suy ra đường thẳng x = 1 là TCN của đồ thị hàm số.
suy ra đường thẳng x = -1 là TCN của đồ thị hàm số.
Vậy đồ thị của hàm số đã cho có tổng cộng 4 đường tiệm cận.
Câu 11:
Chọn D.
Phương trình hoành độ giao điểm:
và .
Câu 13:
Chọn A.
Ta có: với mọi x nên hàm số nghịch biến trên R
Hàm trùng phương luôn có cực trị nên không đồng biến trên R.
với mọi x thuộc tập xác định nên hàm số nghịch biến.
với mọi x thuộc tập xác định nên hàm số đồng biến.
Câu 14:
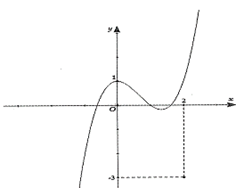
Chọn A.
- Đồ thị hàm số đi qua điểm (0;1) nên loại C.
- Đồ thị hàm số đi qua điểm (1;0) nên loại B, D.
Câu 15:
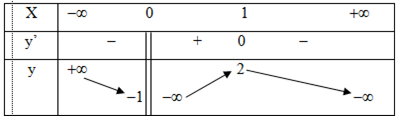
Chọn B.
Từ bảng biến thiên trên ta có ngay thỏa mãn bài toánCâu 16:
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:
Khẳng định nào sau đây là đúng?
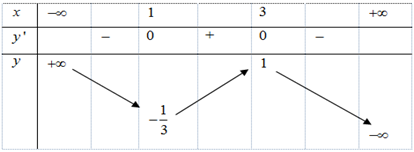
Chọn C.
Nhận thấy hàm số đạt cực đại tại , giá trị cực đại bằng 1 và đạt cực tiểu tại , giá trị cực tiểu bằng .Câu 18:
Chọn A.
Câu 20:
Chọn C.
Biến đổi phương trình về dạng:
.
Đặt , phương trình có dạng:
.
Vậy, phương trình có tập nghiệm là .
Câu 21:
Chọn A.
Ta có số tiền lãi là .Câu 22:
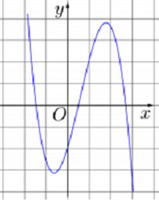
Chọn A.
Dựa vào đồ thị hàm số , ta có nhận xét sau
* Đồ thị hình chữ N ngược nên hệ số a < 0
* Ta có
Đồ thị hàm số đi qua hai điểm cực trị có hoành độ trái dấu nhau nên
* Dễ thấy và đồ thị hàm số cắt Ox tại ba điểm phân biệt nên d < 0
Câu 23:
Chọn D.
. Lúc này hàm số đồng biến trên các khoảng
Vậy hàm số đồng biến trên khoảngCâu 24:
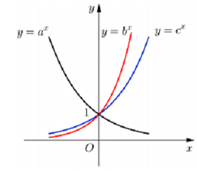
Chọn B.
Dựa vào đồ thị hàm số, ta có nhận xét sau:
* là hàm số nghịch biến trên TXĐ và là các hàm số đồng biến trên TXĐ. Do đó a < b và a < c.
* Tại điểm và tương tự tại điểm
. Do đó b > c > a
Câu 25:
Chọn C.
Sau 3 phút số lượng vi khuẩn A là 625 nghìn con, do đó
Sau t phút số lượng vi khuẩn A là 10 triệu con, do đó
Câu 26:
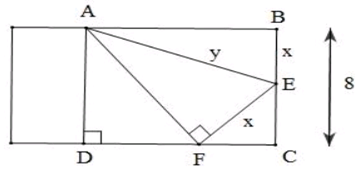
Chọn D.
Đặt
Ta có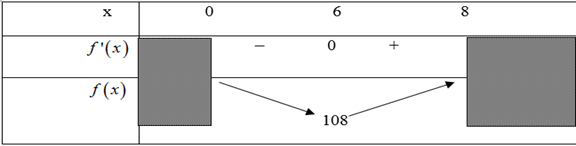
Câu 27:
Chọn D.
Ta có:
Đặt (Do a > b > 1 => 0 < t < 1).
Xét
Khi đó . Ta có:
Do đó
Câu 28:
Chọn C.
Phương trình
Đặt và với .
Khi đó
Xét hàm số trên
Nên hàm số f(t) là hàm số đồng biến trên (1;2). Do đó để (*) có nghiệm thuộc khoảng (0;1) khi và chỉ khi (I) có nghiệm thuộc (1;2) => f(1) < m < f(2) <=> 2 < m <4.
Vậy là giá trị cần tìm.
Câu 31:
Chọn A.
Diện tích xung quanh của hình trụ làCâu 32:
Chọn A.
Ta có:
Câu 33:
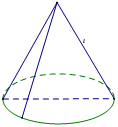
Theo đề suy ra đường sinh l = a, và đường tròn đáy có bán kính . Khi đó , diện tích đáy
VậyCâu 34:
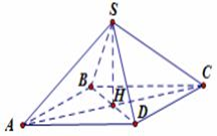
Gọi H là tâm của hình vuông ABCD
Ta có
Câu 35:
Chọn A.
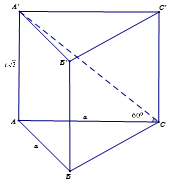
Câu 36:
Chọn D.
Từ giả thiết OA = 4OB, suy ra:
Câu 37:
Câu 38:
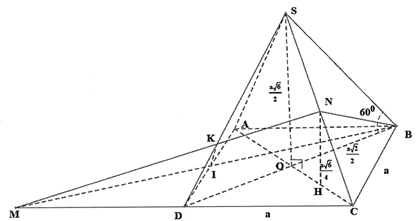
Câu 39:
Chọn D.
Với giả thiết có hai trường hợp là:
hoặc .
Trường hợp 1: Nếu , với ta có:
.
Gọi H, H' theo thứ tự là hình chiếu vuông góc của O lên (d) và (d’), suy ra:
⇒ k không đổi.
Vậy, trong trường hợp này có đúng một phép vị tự tâm O biến (d) thành (d’).
Trường hợp 2: Nếu thì không có phép vị tự tâm O nào biến (d) thành (d’), bởi nếu trái lại với ta có:
⇒ O, M, M' thẳng hàng
, mâu thuẫn.
Vậy, trong trường hợp này không có phép vị tự tâm O nào biến (d) thành (d’).
Do đó, đáp án D là đúng
Câu 40:
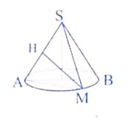
Gọi H là hình chiếu vuông góc của M lên SA.
Ta có, diện tích ΔSAM được cho bởi:
.
Do đó, diện tích ΔSAM đạt giá trị lớn nhất khi:
MH đạt giá trị lớn nhất ⇔ MH = MS
.
Tức M là giao điểm của đường tròn đáy hình nón với mặt phẳng (P) qua S và vuông góc với SA.
Từ giả thiết suy ra tồn tại điểm M trên đường tròn đáy thỏa mãn yêu cầu đề bài.Câu 41:
Hàm số đã cho có hai điểm cực trị có hai nghiệm phân biệt ó (*)
Giả sử:
thỏa mãn (*)
Câu 42:
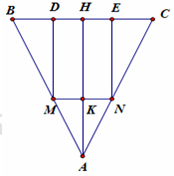
Ta có:
Theo đề, thể tích khối trụ là:
