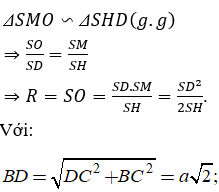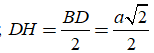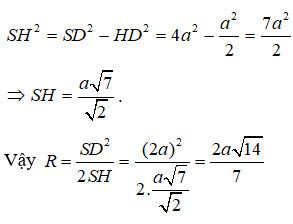Đề kiểm tra 45 phút Toán 12 Chương 2 Hình học có đáp án (Đề 4)
-
2459 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
I. Trắc nghiệm ( 6 điểm)
Cho mặt cầu S(O; R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Đường thẳng Δ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?
Chọn A.
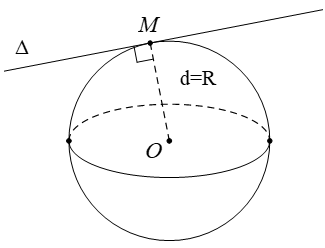
Đường thẳng Δ tiếp xúc với S( O; R) khi d = R.
Câu 2:
Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là:
Chọn C
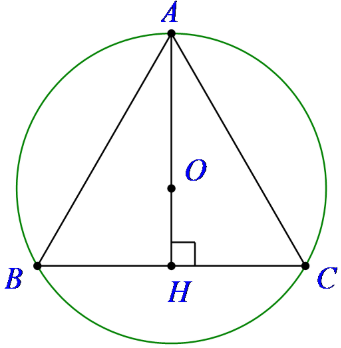
AH là đường cao trong tam giác đều cạnh a nên
Gọi O là tâm mặt cầu ngoại tiếp ΔABC, thì O ∈ AH và 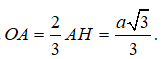
Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là 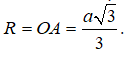
Vậy thể tích của khối cầu tương ứng là:
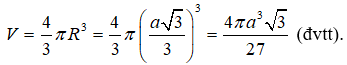
Câu 3:
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Tính diện tích xung quanh của hình nón.
Chọn B.
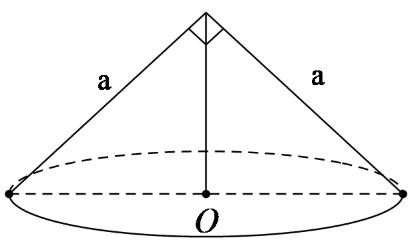
Thiết diện qua trục là một tam giác vuông cạnh a nên đường sinh của hình nón là l = a.
Đường kính của đường tròn đáy là:
![]()
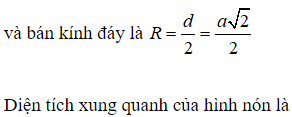
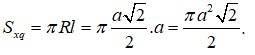
Câu 4:
Cắt khối nón bởi một mặt phẳng qua trục tạo thành một tam giác ABC đều có cạnh bằng a, biết B, C thuộc đường tròn đáy. Thể tích của khối nón là:
Chọn C
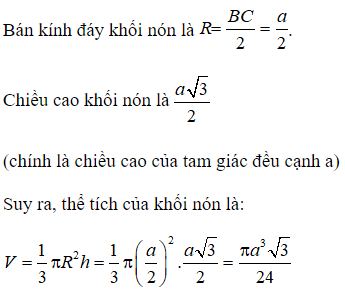
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
Chọn A.
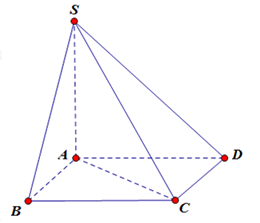
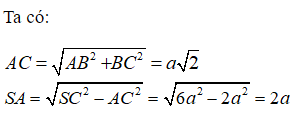
Hình nón tròn xoay được tạo thành là một hình nón có bán kính đáy là R = AC, đường cao h = SA có thể tích là:
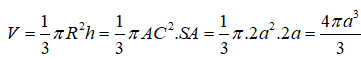
Câu 6:
Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức luôn đúng là?
Chọn A.
Đường sinh và chiều cao của một hình trụ luôn bằng nhau nên đẳng thức đúng là l = h
Câu 7:
Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a, có diện tích xung quanh là:
Chọn C.
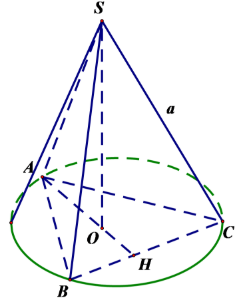
Khi đó, SO là trục của tam giác ABC nên SO⊥(ABC)
Gọi AO ∩ BC = H
Ta có:
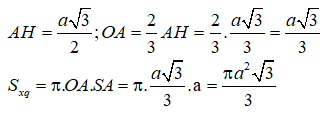
Câu 8:
Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng a và thiết diện đi qua trục là một hình vuông.
Chọn A.
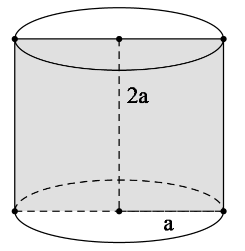
Theo bài ra thiết diện qua trục của hình trụ là hình vuông nên hình trụ có bán kính đáy là a, chiều cao 2a.
Do đó thể tích khối trụ là: V = πR2h = πa2.2a = 2πa3.
Câu 9:
II. Tự luận ( 4 điểm)
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh của hình nón và thể tích V của khối nón tương ứng là:
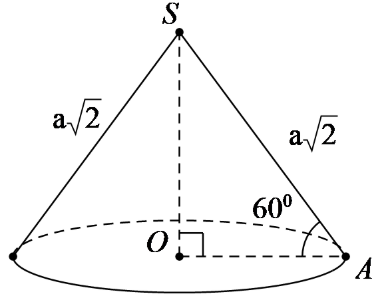
Gọi A là một điểm thuộc đường tròn đáy hình nón.
Theo giải thiết ta có đường sinh và góc giữa đường sinh và mặt phẳng đáy là .
Trong tam giác vuông SAO, ta có:
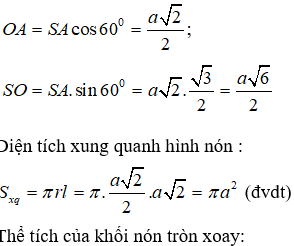
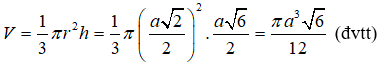
Câu 10:
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
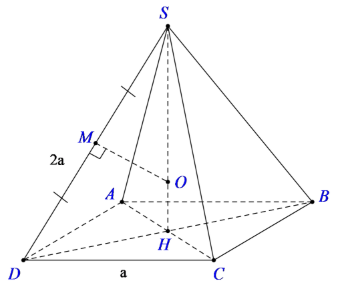
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông ABCD.
Gọi M là trung điểm của SD, trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O. Suy ra; OS = OD (1)
Mà O thuộc trục SH của hình vuông ABCD nên:
OA = OB = OC = OD (2)
Từ (1) và (2) suy ra: OA = OB = OC = OD = OS
Do đó, O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là R = SO
Ta có: