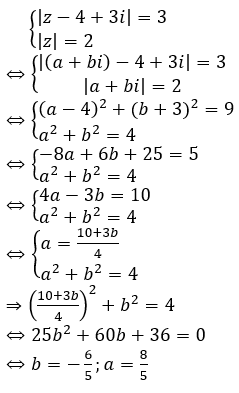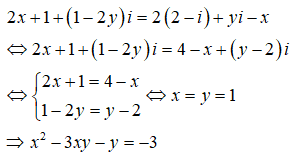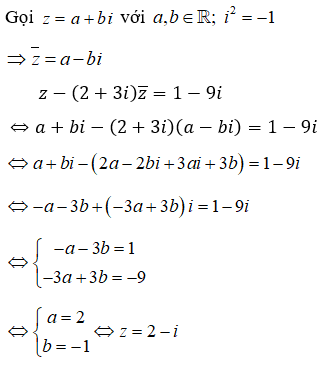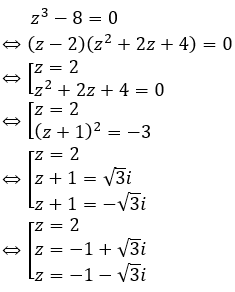Đề kiểm tra 45 phút Toán 12 Chương 4 Giải tích có đáp án (Đề 2)
-
2401 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho số phức Số phức đối của z có tọa độ điểm biểu diễn là
Chọn A.
z = 5 - 4i ⇔ -z = -5 + 4i.
Vậy điểm biểu diễn của -z là (-5;4)
Câu 2:
Số nào trong các số phức sau là số thuần ảo?
Chọn C.
= là số thuần ảo
= 20 là số thực
= là số thực
= 6 là số thực
Câu 5:
Cho số phức Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là:
Chọn D.
Số phức liên hợp của z là có phần thực là -1, phần ảo là 2.
Vậy điểm biểu diễn số phức liên hợp là M(-1;2)
Câu 6:
Phần thực, phần ảo của số phức z thỏa mãn lần lượt là
Chọn A.

Phần thực, phần ảo của z lần lượt là 1;1.
Câu 9:
Khai căn bậc hai số phức z = -3 + 4i có kết quả:
Chọn A.
Giả sử w = x + yi(x, y ∈ R) là một căn bậc hai của số phức z = -3 + 4i.
Ta có:
![]()
![]()
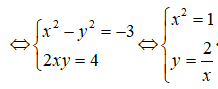
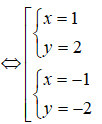
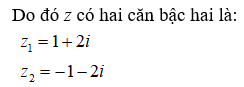
Câu 11:
Giả sửlà hai nghiệm của phương trình và A, B là các điểm biểu diễn của . Tọa độ trung điểm I của đoạn thẳng AB là:
Chọn D.
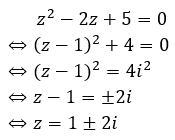
Do đó, tọa độ 2 điểm biểu diễn của z1; z2 là: A(1;2) và B(1;-2)
Do đó tọa độ trung điểm I của đoạn thẳng AB là I(1;0).
Câu 12:
Phương trình có một nghiệm phức là Tổng 2 số a và b bằng:
Chọn C
Vì z = 1 + 2i là một nghiệm của phương trình z2 + az + b = 0 nên ta có:
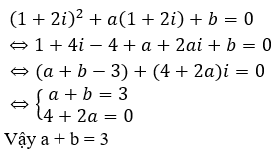
Câu 13:
Cho phương trình Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng Giá trị a là:
Chọn D
Gọi z1, z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
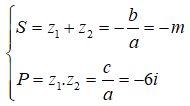
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
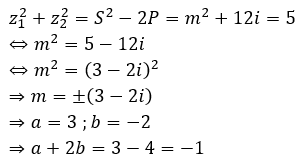
Câu 14:
Cho số phức Để điểm biểu diễn của z nằm trong dải (-3i;3i) như hình 2 thì điều kiện của a và b là:

Chọn D.
Các số phức trong dải đã cho có phần ảo trong khoảng (-3;3), phần thực tùy ý
Câu 15:
Tập hợp các điểm M biểu diễn số phức z sao cho là:
Chọn B.
Gọi M (a; b) là điểm biểu diễn số phức z = a + bi (a, b ∈ R)
Ta có :

Câu 16:
Cho số phức z thỏa Khi đó phần thực và phần ảo của z lần lượt là
Chọn D.
Ta có : 1 + i + i2 + i3 + ... + i2016 là tổng của cấp số nhân với số hạng đầu u1 = 1, công bội q = i.
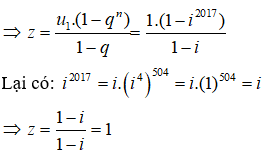
Do đó, phần thực và phần ảo của z lần lượt là: 1 và 0.
Câu 17:
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện:
Chọn B.
Gọi M(x; y) là điểm biểu diễn của số phức z = x + yi trong mặt phẳng phức(x, y ∈ R).
Theo đề bài ta có
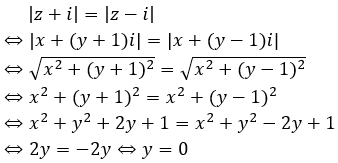
Vậy tập hợp các điểm M là đường thẳng y = 0 hay trục Ox
Câu 20:
Cho Số phức z có module nhỏ nhất có phần thực bằng?
Chọn A.
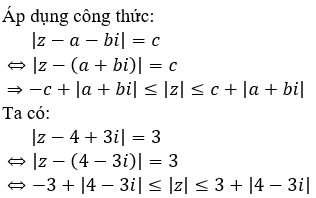
![]()
![]()
+ Tìm Số phức z có module nhỏ nhất là: