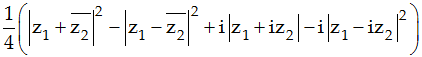100 câu trắc nghiệm Số phức nâng cao (P3)
-
4025 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
Chọn D.
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, x, y ∈ R
Gọi A là điểm biểu diễn số phức 2
Gọi B là điểm biểu diễn số phức -2
Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
Ta có AB = 4.
Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0) tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là 
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình 
Câu 2:
Cho số phức z thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z là?
Chọn A.
Gọi M(x; y) , F1= ( -2; 0) và F2( 2; 0).
Ta có |z + 2| + |z – 2| = 8
Hay MF1+ MF2 = 8.
Do đó điểm M(x; y) nằm trên elip (E ) có 2a = 8 nên a = 4
ta có F1F2 = 2c nên 4 = 2c hay c = 2
Ta có b2 = a2 - c2 = 16 - 4 = 12
Vậy tập hợp các điểm M là elip 
Câu 3:
Tìm nghiệm của phương trình:
Chọn B.
Điều kiện: z 3i
Đặt 
. Phương trình đã cho trở thành: t2 - 3t – 4 = 0
Suy ra: t = 4 hoặc t = -1
Với t = 4 thì 
Hay iz + 3 = 4( z – 3i)
Không thỏa mãn.
Với t = -1 thì 
Suy ra: iz + 3 = -1 ( z - 3i)
( 1 + i) z = -3 + 3i hay z = 3i (không thỏa mãn)
Vậy không có z thỏa mãn.
Câu 4:
Tìm nghiệm của phương trình: ( z + 3 - i)2 - 6( z + 3 - i) + 13 = 0
Chọn D.
Đặt t = z + 3 - i. Phương trình đã cho trở thành: t2 - 6t + 13 = 0
Suy ra : t = 3 + 2i hoặc t = 3 - 2i
Với t = 3+ 2i thì z + 3 – i = 3 + 2i hay z = 3i
Với t = 3- 2i thì z + 3 – i = 3 -2i hay z = - i
Câu 5:
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| =| + 2 + 4i| và là số thuần ảo.
Chọn C.
Giả sử z = a+ bi thì 
khi và chỉ khi a = b - 4 (1)
Với a ≠ 0 hoặc b ≠ 1, ta có:
Vì 
là số thuần ảo nên a2 - ( b - 1) 2 = 0 khi và chỉ khi a = b - 1 hoặc a = 1 - b
Kết hợp (1) ta có a = -3/2 và b = 5/2.
Nên số phức đó là 
Vậy .
Câu 6:
Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức z thỏa mãn 
là đường tròn C. Diện tích S của đường tròn C bằng bao nhiêu?
Chọn D.
+ Gọi M(x; y) là điểm biểu diễn số phức z = x + yi
Từ giả thiết ta có:
x2 + y2 + x + yi + x - yi = 0
Hay x2 + y2 + 2x = 0
⇒ Tập hợp các số phức z thỏa mãn điều kiện đầu bài là đương tròn tâm I (-1; 0) và bán kính R = 1.
Nên diện tích cần tìm là S = πR2 = π.
Câu 7:
Tính giá trị của 
biết z1; z2; z3; z4 là nghiệm phức của phương trình ( 5z2 - 6iz - 2)( -3z2+ 2iz) = 0.
Chọn B.
Phương trình đã cho tương đương với -3z2 + 2iz = 0 ( 1) hoặc 5z2 - 6iz - 2 = 0 ( 2)
Giải (2): ta có 
Suy ra 
Do đó: 
Câu 8:
Tính mô-đun của số phức z, biết 
và z có phần thực dương.
Chọn D.
Giả sử z = x + yi (x, y R); từ giả thiết : 
Nên ( x + yi) 3+ 12i = x - yi
Hay x3 - 3xy2+ ( 3x2y - y3 +12) i = x - yi
Ta có hệ phương trình là x3 - 3xy2 = x (1) và 3x2y - y3 + 12 = - y ( 2)
Do x > 0 nên từ (1) x2 = 3y2+ 1. Thế vào (2) ta được:
3( 3y2 + 1) y - y3 + 12 = -y
Hay 2y3+ y + 3 = 0 (3)
Giải phương trình (3) ta được y = -1; x2 = 4. Do x > 0 nên x = 2.
Vậy z = 2 - i và 
Câu 9:
Giải phương trình sau: ( z2 + z) 2 + 4( z2+ z) - 12 = 0
Chọn C.
Đặt t = z2 + z; Phương trình đã cho trở thành
Với 
Với 
Vậy phương trình đã cho có 4 nghiệm.
Câu 10:
Giải phương trình sau: ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) - 3z2 = 0
Chọn D.
Ta có: ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) - 3z2 = 0
Hay ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) + z2 – 4z2 = 0
[(z2 + 3z + 6) + z]2 - ( 2z)2 = 0
[z2 + 4z + 6 ]2 - ( 2z)2 = 0
Suy ra: (z2 + 4z + 6 - 2z) (z2 + 4z + 6 + 2z) = 0
Vậy nghiệm của phương trình là: 
Câu 11:
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
Chọn D.
Phương trình đã cho tương đương với phương trình
z( z + 2) ( z - 1) ( z + 3) = 10
Hay ( z2 + 2z) ( z2 + 2z - 3) = 10
Đặt t = z2 + 2z. Khi đó phương trình trở thành: t2 - 3t – 10 = 0.
Vậy phương trình có các nghiệm: 
Tổng tất cả các phần thực của các nghiệm phương trình đã cho là:
-1+ ( -1) + (-1) + ( -1) = -4.
Câu 12:
Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z1 = 1 + 2i; z2 = -2 + 5i ; z3 = 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
Chọn B.
Ta có A(1 ;2) ; B(-2 ; 5),C(2 ;4).
Gọi D(x ; y).
Ta có 
Để ABCD là hình bình hành thì 
Vậy z = 5 + i.
Câu 13:
Cho 3 điểm A ; B ;C lần lượt biểu diễn cho các số phức z1 ; z2 ; z3 .Biết | z1| = | z2| = | z3| và z1+ z2= 0 . Khi đó tam giác ABC là tam giác gì?
Chọn B.
Vì z1+ z2= 0 nên z1 ; z2 là hai số phức đối nhau, do đó hai điểm A: B đối xứng qua gốc O ( tức O là trung điểm của đoạn thẳng AB).
Lại có | z1| = | z2| = | z3| 
Vậy tam giác ABC có độ dài đường trung tuyến bằng một nửa cạnh huyền nên vuông tại C.
Câu 14:
Xét số phức z thỏa mãn 2|z - 1 | + 3| z - i | . Mệnh đề nào dưới đây đúng?
Chọn D.
Giả sử z = x + yi có điểm biểu diễn là M(x; y).
Số phức z - 1 có điểm biểu diễn A(x - 1; y) và z - i có điểm biểu diễn là B(x; y - 1).
Ta có
Mà 2OA + 3OB = 2OA + 2OB + OB ≥ 2 AB + OB (2)
Từ (1) và (2) suy ra 2AB + OB ≤ 2AB khi và chỉ khi B và O trùng nhau
Khi đó: x = 0 và y = 1.
Khi đó z = i ⇒ |z| = 1.
Câu 16:
Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thoả mãn điều kiện: 
là hình gì?
Chọn B.
Đặt z = a + bi 
Theo giả thiết 
⇔ 2|a + (b – 1)i| = |2(b + 1)i|
Hay a2 + ( b - 1) 2 = ( b + 1)2
Suy ra: a2 = 4b
Quỹ tích các số phức z là một đường Parabol.
Câu 17:
Cho số phức z = m - 2 + ( m2 - 1) i với m là số thực. Gọi (C) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Tính diện tích hình phẳng giới hạn bởi (C) và Ox.
Chọn B.
Gọi M(x; y) là điểm biểu diễn số phức z.
Ta có: 
Diện tích cần tìm:
Câu 18:
Gọi M là điểm biểu diễn của số phức z thỏa mãn 3| z + i| = | 2 - z + 3i | . Tập hợp tất cả những điểm M như vậy là
Chọn A.
Gọi số phức z = x + yi có điểm biểu diễn là M(x; y) trên mặt phẳng tọa độ:
Theo đề bài ta có:
⇔ |3(x + yi) + 3i| = |2(x – yi) – (x + yi) + 3i|
⇔ |3x + (3y + 3)i| = |x + (3 – 3y)i|
Hay 9x2 + ( 3y + 3) 2 = x2 + ( 3 - 3y) 2
Suy ra: 8x2 + 36y = 0 hay y = -2/9 x2
Vậy tập hợp các điểm M(x; y) biểu diễn số phức z theo yêu cầu của đề bài là parabol 
Câu 19:
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện 
Chọn D.
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi
Ta có: 
Câu 20:
Có bao nhiêu số phức z thỏa mãn 
và z2 là số thuần ảo.
Chọn C.
Đặt z = x + yi
Ta có: 
Mặt khác: z2 = ( x + yi) 2 = x2 - y2 + 2xyi là số thuần ảo nên x2 - y2 = 0
Ta có hệ: 
Vậy các số phức cần tìm là: z = 1+ i; z = 1 - i; z = -1 + i và z = -1 - i.
Câu 21:
Tính tổng phần ảo các số phức z thỏa mãn |z| = 5 và phần thực của nó bằng 2 lần phần ảo.
Chọn A.
Gọi số phức cần tìm là z = x + yi.
Ta có:
hay x2 + y2 = 25 (*)
Mặt khác: Số phức có phần thực của nó bằng 2 lần phần ảo nên x = 2y
thay vào phương trình (*) ta được: 5y2 = 25 hay 
Vậy số phức cần tìm là: 
Do đó tổng các phần ảo là:
Câu 22:
Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và 
. Hỏi có bao nhiêu số phức z thỏa mãn
Chọn B.
Gọi số phức cần tìm là z = a + bi.
Ta có ( 1 - 3i) z = ( 1 - 3i) ( a + bi)
= a + 3b - 3ai + bi = a + 3b + ( b - 3a) i
+ Do ( 1 - 3i) z là số thực nên b - 3a = 0 hay b = 3a
+ ta có 
⇔|a – 2 + (-b + 5)i| = 1
Hay ( a - 2) 2 + ( 5 - 3a) 2 = 1
(thỏa mãn)
Vậy có hai số phức z thỏa mãn là z = 2 + 6i và
Câu 23:
Tìm số phức z biết |iz + 1 | = và ( 1 + i) z + 1 – 2i là số thuần ảo.
Chọn C.
Đặt 
và 
khi đó ta có:
Số phức này là số ảo, do đó ta có:
Thay vào (*) ta có z = -1 và z = 1+ 2i.
Câu 24:
Biết z1; z2 là hai số phức thỏa điều kiện:
. Tính z1+ z2
Chọn A.
Gọi số phức z = a+ bi.
Từ giả thiết suy ra:
2( a - bi + 1) + a + bi - 1= ( 1- i) ( a2 + b2)
Tương đương: ( 3a + 1) – bi = a2 + b2 - i( a2 + b2)
Có hai số phức cần tìm z1= i; 
Suy ra: 
Câu 25:
Biết z1; z2 là số phức thỏa mãn:
.
Tính 
Chọn A.
Gọi z = a+ bi
Ta được: ( a+ bi+ 1) 2+|a + bi – 1|2 + 10i = a - bi + 3
Tương đương: ( 2a2- a - 1) + ( 2ab + 3b + 10) i = 0
Vậy z = 1 - 2i và z = - 5i.
Suy ra 