28 câu hỏi trắc nghiệm thuộc Bài tập Hình học Khối đa diện cơ bản, nâng cao có lời giải chi tiết (P4) - qa.haylamdo.com

Bài tập Hình học Khối đa diện cơ bản, nâng cao có lời giải chi tiết

Bài tập Hình học Khối đa diện cơ bản, nâng cao có lời giải chi tiết (P4)

3067 lượt thi
28 câu hỏi
40 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho khối chóp S.ABCD có đáy là hình bình bành thể tích bằng 1. Gọi M là điểm đối xứng của C qua B;N là trung điểm cạnh SC. Mặt phẳng (MDN) chia khối chóp S.ABCD thành hai khối đa diện, thể tích của khối đa diện chứa đỉnh S bằng

A. $\frac{5}{6}$

B. $\frac{5}{8}$

C. $\frac{12}{19}$

D. $\frac{7}{12}$

Chọn D

Ta có:

Mặt khác

Vậy

Câu 2:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông, biết BA = BC = 2a, cạnh bên SA = $2 a \sqrt{2}$ vuông góc với đáy. Diện tích mặt cầu ngoại tiếp hình chóp đã cho bằng

A. $8 π a^{2}$

B. $16 π a^{2}$

C. $4 π a^{2}$

D. $\frac{17}{12}$

Câu 3:

Cho khối lăng trụ tam giác đều ABC. A'B'C' có thể tích bằng $\sqrt{3}$ cosin góc giữa hai đường thẳng AB’ và BC’ bằng $\frac{31}{34}$ Chiều cao của lăng trụ đã cho bằng

A. 2

B. 6

C. 3

D. 4

Chọn D

Đặt AB = a, AA' = h ta có

=

Vì vậy

h = 4a

Câu 4:

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tồn tại một điểm M nằm bên trong hình chóp và cách đều tất cả các mặt của hình chóp một khoảng bằng h. Tính h.

Chọn B

Thể tích của khối chóp tứ giác đều tất cả các cạnh bằng a là

Câu 5:

Cho khối chóp tứ giác đều P.ABCD có tất cả các cạnh bằng 2 được đặt nằm bên trên khối lập phương ABCD.EFGH (như hình vẽ). Côsin góc giữa hai mặt phẳng (PAB) và (AEFB) bằng

A. - $\frac{\sqrt{6}}{3}$

B. $\frac{\sqrt{3}}{3}$

C. $\frac{2 \sqrt{2}}{3}$

D. $\frac{1}{3}$

Chọn A

Gọi M, N lần lượt là trung điểm AB, EF ta có

Câu 6:

Cho khối hộp ABCD.A′B′C′D′ có tất cả các cạnh bằng 2a, có đáy là hình vuông và cạnh bên tạo với mặt phẳng đáy khối hộp một góc bằng $60^{o}$ Thể tích khối hộp bằng

A. 8 $a^{3}$

B. $2 \sqrt{3} a^{3}$

C. $8 \sqrt{3} a^{3}$

D. $4 \sqrt{3} a^{3}$

Chọn D

Có chiều cao khối hộp là

Câu 7:

Thể tích của khối chóp tứ giác đều S .ABCD có cạnh đáy bằng 2a, tam giác SAC vuông bằng

Chọn A

Có

Câu 8:

Cho khối chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Gọi M, N lần lượt là các điểm trên các cạnh SB, SD sao cho MS = MB, ND = NS = 2. Mặt phẳng (CMN) chia khối chóp đã cho thành hai phần, thể tích của phần có thể tích nhỏ hơn bằng

Chọn D

Ta có:

và

Khi đó

Câu 9:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S. ABCD bằng

Chọn B

Có đường cao của hình chóp đồng thời là đường cao tam giác đều

Câu 10:

Cho hình lăng trụ đứng ABC.A’B’C’ tất cả các cạnh bằng $\sqrt{2}$ a Thể tích của khối lăng trụ ABC.A’B’C’ bằng

Chọn A

Có

Câu 11:

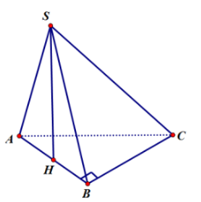
Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA ⊥ (ABC), cạnh bên SC tạo với (ABC) một góc 60⁰ và H là trung điểm của AB. Biết rằng khoảng cách từ H đến (SBC) bằng $\sqrt{15}$ a Thể tích của khối chóp S.ABC bằng

A. 750 $a^{3}$

B. 250 $a^{3}$

C. 400 $a^{3}$

D. 500 $a^{3}$

Chọn B

Gọi E là trung điểm BC, F là chân đường cao của A trên SE.

Có

Có

Tam giác SAE vuông nên

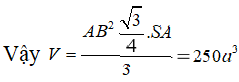
Câu 12:

Cho hình lập phương ABCD.A'B'C'D' có khoảng cách giữa hai đường thẳng AB′ và BD bằng $\frac{2 \sqrt{3} a}{3}$

Thể tích của khối lập phương ABCD.A’B’C’D’ bằng

A. 8 $a^{3}$

B. $a^{3}$

C. $3 \sqrt{3} a^{3}$

D. $\frac{3 \sqrt{6}}{4} a^{3}$

Chọn A

Trên mặt đáy (ABCD) dựng hình bình hành AEBD như hình vẽ, Gọi H, K lần lượt là hình chiếu của B lên AE, B’H.

Khi đó

Câu 13:

Cho khối đa diện (H) như hình vẽ bên, trong đó ABC.A’B’C’ là khối lăng trụ tam giác đều có tất cả các cạnh bằng 1 và S.ABC là khối chóp tam giác đều có độ dài cạnh bên bằng $\frac{2}{3}$ Thể tích của khối đa diện đã cho bằng

Chọn D

Câu 14:

Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, $∠ A B C = 60 °$ Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm của tam giác ABC. Gọi M, N lần lượt là trung điểm của AB, SD. Biết cosin góc giữa hai đường thẳng CN và SM bằng $\frac{2 \sqrt{26}}{13}$ Thể tích khối chóp S.ABCD bằng

Chọn D

Gọi O = AC $\cap$ BD và G là trọng tâm tam giác ABC ta có SG $⊥$ (ABCD)

Đặt SG = h. Gọi P là trung điểm DM. Ta có

Ta có:

Vậy ta có phương trình

Vậy

Câu 15:

Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng $3 \sqrt{6}$ , chiều cao bằng $3 \sqrt{3}$ . Khoảng cách từ đỉnh C đến mặt phẳng (SAB) bằng

A. 6

B. $3 \sqrt{2}$

C. 3

D. 2 $\sqrt{3}$

Chọn A

Gọi O là giao điểm của AC và BD. Có

= 2d(O,(SAB))

Ta có OA, OB, OS đôi một vuông góc nên với

=> d(C,(SAB)) = 6

Câu 16:

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = $a \sqrt{3}$ , AC = 2a Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABC). Tính theo a thể tích khối chóp S.ABC

Chọn A

Gọi H là trung điểm AB, có

Khi đó thể tích khối chóp S>ABC là

Câu 17:

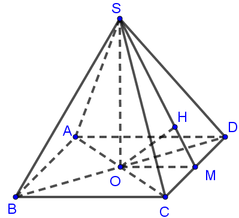
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a. Khoảng cách từ O đến mặt phẳng (SCD) bằng

A. $\frac{\sqrt{2} a}{2}$

B. $\sqrt{3}$ a

C. $\frac{\sqrt{5} a}{5}$

D. $\frac{\sqrt{6} a}{3}$

Chọn A

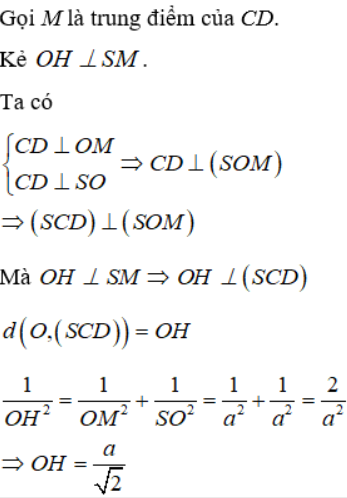
Câu 18:

Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD. Tính thể tích V của khối chóp A.GBC.

A. V = 3

B. V = 4

C. V = 6

D. V = 5

Chọn B

Ta có

Câu 19:

Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông cân tại C, AB = 2a. Trên các đoạn thẳng AB′, A′C có lần lượt các điểm M, N và P, Q sao cho MNPQ là tứ diện đều. Tính thể tích của khối lăng trụ ABC.A′B′C′.

Chọn C

Gọi h là độ dài cạnh bên của lăng trụ đứng đã cho.

Vì MNPQ là tứ diện đều nên

= 0

*Chú ý một khối tứ diện đều (tất cả các cạnh bằng nhau) hoặc một khối tứ diện gần đều (độ dài cặp cạnh đối bằng nhau) thì cặp cạnh đối của chúng vuông góc với nhau (xem chương góc và khoảng cách).

*Chú ý tích vô hướng cho hai véctơ cùng gốc

Câu 20:

Cho tứ diện đều ABCD có cạnh bằng 3a. Hình nón (N) có đỉnh A và đường tròn đáy là đường ngoại tiếp tam giác BCD. This diện tích xung quanh $S_{x q}$ của N

Chọn B

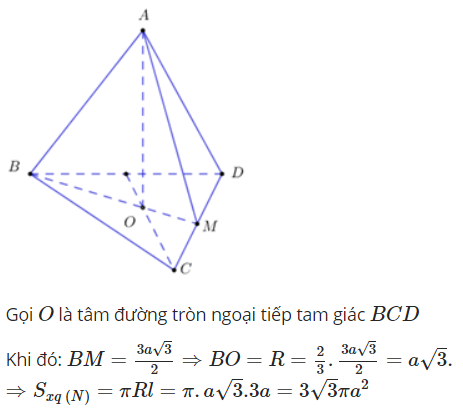
Câu 21:

Tính thể tích V của khối chóp lục giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy băng 30 độ. Thể tích khối chóp bằng

Chọn A

Câu 22:

Cho khối chóp tam giác S.ABC có AB = AC = a, $\hat{B A C} = 120 °$ , $\hat{S B A} = \hat{S C A} = 90 °$ Góc giữa SB và mặt phẳng (ABC) bằng $60 °$ Thể tích khối chóp S.ABC bằng

Chọn B

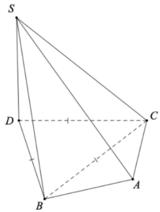
Hạ SD ⊥ (ABC). Ta dễ dàng tính được BC = $a \sqrt{3}$

Ta có:

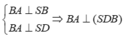
⇒ BA ⊥ DB ⇒ $\hat{D B C}$ = $60 °$ . Tương tự ta có:

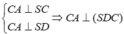
⇒ CA ⊥ DC ⇒ $\hat{C D B} = 60 °$

Do đó ∆CBD đều

$\Rightarrow$

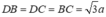
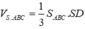
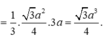
Câu 23:

Kim tự tháp Ai cập được xây dựng vào khoảng 2500 năm trước Công Nguyên là một khối chóp tứ giác đều có chiều cao 147m, cạnh đáy dài 230m. Thể tích của khối chóp đó bằng

A. V = 2592100 $(m^{3})$

B. V = 7776300 $(m^{3})$

C. V = 2592300 $(m^{3})$

D. V = 3888150 $(m^{3})$

Chọn A

Ta có

Câu 24:

Thể tích của khối lăng trụ đứng ABC.A'B'C' có AB = AC = AA' = 1, BC = $\sqrt{2}$ bằng

A. $\frac{1}{2}$

B. 1

C. $\frac{1}{6}$

D. $\frac{1}{3}$

Chọn A

Có

Câu 25:

Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a,cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng $60^{o}$ . Thể tích của khối chóp đã cho bằng

Chọn D

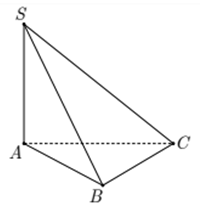
Ta có

Vậy

Câu 26:

Cho tứ diện ABCD có AB = 2a, tam giác BCD vuông tại C, BD = 2a, BC = a và $2 A C^{2} - A D^{2} = 6 a^{2}$ Gọi E là trung điểm cạnh BD. Góc giữa hai đường thẳng AB và EC bằng

A. $30^{o}$

B. $90 °$

C. $45^{o}$

D. $60^{o}$

Chọn D

Gọi F là trung điểm cạnh AD có

Tam giác $∆ E F C$ có

Câu 27:

Cho hình chóp tứ giác đều S. ABCD có độ dài cạnh đáy bằng 1. Gọi E,F lần lượt là trung điểm các cạnh SA và BC Biết rằng $E F = \frac{\sqrt{6}}{2}$ sin của góc giữa đường thẳng EF và mặt phẳng (SPD) bằng

Chọn A

Khi đó

Câu 28:

Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng $\sqrt{3} a, \hat{B A D} = 60^{o}$ ,SA vuông góc với mặt đáy, góc giữa đường thẳng SC và mặt đáy bằng $45^{o}$ Gọi M,N lần lượt là trung điểm các cạnh CD và AB Khoảng cách từ điểm B đến mặt phẳng (SMN) bằng

Chọn C

Ta có

Do

Có

Ta lại có

Và

Bắt đầu thi ngay

Bài thi liên quan