256 Bài tập Hàm số mũ và Logarit cực hay có lời giải chi tiết (P2)
-
4764 lượt thi
-
50 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Số nghiệm thực phân biệt của phương trình là
Chọn đáp án B
Phương pháp
Giải phương trình mũ:
()
Cách giải
Ta có:
Câu 2:
Tập nghiệm của bất phương trình là
Chọn đáp án B
Phương pháp
Giải bất phương trình mũ:
.
Cách giải
Ta có: .
Câu 3:
Nếu thì biểu thức bằng
Chọn đáp án C
Phương pháp
Sử dụng các công thức
(giả sử các biểu thức là có nghĩa).
Cách giải
![]()
![]()
Câu 5:
Tập hợp các số thực m để phương trình có nghiệm thực là
Chọn đáp án D
Phương pháp
Hàm số có tập giá trị là .
Cách giải
Hàm số có tập giá trị là nên phương trình có nghiệm thực với mọi giá trị của m.
Câu 6:
Cho phương trình . Nghiệm nhỏ nhất của phương trình thuộc khoảng
Chọn đáp án A.
ĐK:
![]()
![]()
![]()
![]()
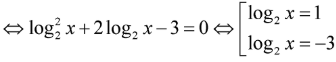
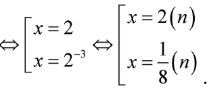
Nghiệm dương nhỏ nhất là .
Câu 9:
Tổng các nghiệm của phương trình
Chọn đáp án D.
Phương trình tương đương
![]()
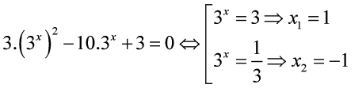
Tổng các nghiệm của phương trình bằng .
Câu 11:
Tập nghiệm S của bất phương trình là.
Chọn đáp án A.
Điều kiện: .
Ta có:
So với điều kiện ta có tập nghiệm .
Câu 12:
Giá trị p, q là các số thực dương thỏa mãn . Tìm giá trị của p/q
Chọn đáp án A.
Đặt
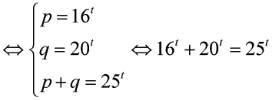
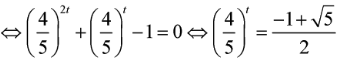
Suy ra .
Câu 13:
Cho hai hàm số (với a, b là hai số thực dương khác 1) có đồ thị lần lượt là như hình vẽ. Khẳng định nào sau đây đúng?
Chọn đáp án A
Phương pháp
Quan sát các đồ thị hàm số, nhận xét tính đồng biến nghịch biến và suy ra điều kiện của a, b.
Cách giải
Đồ thị hàm số có hướng đi lên từ trái qua phải nên hàm số đồng biến hay .
Đồ thị hàm số có hướng đi xuống từ trái qua phải nên hàm số nghịch biến hay .
Do đó .
Câu 14:
Tìm nghiệm của phương trình .
Chọn đáp án D
Phương pháp
Sử dụng công thức .
Cách giải
Ta có: .
Câu 15:
Cho a là số thực dương bất kì khác 1. Tính .
Chọn đáp án C
Phương pháp
Sử dụng các công thức lũy thừa thu gọn biểu thức dưới dấu logarit và sử dụng công thức .
Cách giải
Ta có: .
Câu 16:
Cho phương trình có hai nghiệm . Tính .
Chọn đáp án C
Phương pháp
Coi phương trình đã cho là bậc hai ẩn , giải phương trình tìm x và kết luận.
Cách giải
Ta có:
![]()
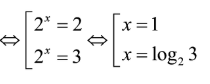
Do đó .
Câu 17:
Biết bất phương trình có tập nghiệm là đoạn . Giá trị của a+b bằng
Chọn đáp án C
Phương pháp
Giải bất phương trình bằng cách đưa về bất phương trình bậc hai, ẩn là .
Cách giải
Điều kiện:
Ta có:
![]()
![]()
![]()
![]()
Do đó tập nghiệm của bất phương trình là
![]()
![]()
Câu 18:
Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn theo quý (3 tháng), lãi suất 2% một quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý số tiền lãi sẽ được nhập vào gốc để tính lãi cho quý tiếp theo. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được 1 năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây?
Chọn đáp án A
Phương pháp
Sử dụng công thức lãi kép với r là lãi suất, là số tiền ban đầu, A là số tiền thu được sau n kì hạn.
Cách giải
Số tiền cả gốc và lãi người đó nhận được sau khi gửi 100 triệu trong 6 tháng đầu là triệu đồng.
Sau 6 tháng người đó gửi thêm 100 triệu đồng nên số tiền gốc lúc này là
Sau 6 tháng còn lại, thì người đó nhận được tổng số tiền là
triệu đồng.
Câu 19:
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; còn để pha chế 1 lít nước táo, cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm và mỗi lít nước táo nhận được 80 điểm. Gọi x, y lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế sao cho tổng điểm đạt được là lớn nhất. Tính
Chọn đáp án C
Phương pháp
- Lập hệ bất phương trình ẩn x, y dựa vào điều kiện đề bài.
- Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ.
- Tìm x, y để biểu thức tính số điểm đạt GTLN (tại một trong các điểm mút).
Cách giải
Gọi x, y lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế ().
Để pha chế x lít nước cam thì cần đường, x lít nước và hương liệu.
Để pha chế y lít nước táo thì cần đường, y lít nước và hương liệu.
Theo bài ra ta có hệ bất phương trình:
(*)
Số điểm đạt được khi pha x lít nước cam và y lít nước táo là: .
Bài toán trở thành tìm x, t thỏa để đạt GTLN.
Ta biểu diễn miền nghiệm của (*) trên mặt phẳng tọa độ như sau:
Miền nghiệm là ngũ giác ACJIH
Tọa độ các giao điểm
.
sẽ đạt max, min tại các điểm đầu mút nên thay tọa độ từng giao điểm vào tính ta được:
;
Vậy
khi
Câu 20:
Với a và b là hai số thực dương, a khác 1. Giá trị của bằng
Phương pháp
Sử dụng công thức :
Cách giải
Ta có:
Chọn B.
Câu 21:
Tập nghiệm S của bất phương trình là
Phương pháp
Giải bất phương trình mũ bằng cách loganepe hai vế.
Cách giải
Ta có:
![]()
![]()
Chọn D.
Câu 22:
Cho phương trình . Nghiệm nhỏ nhất của phương trình thuộc khoảng
Phương pháp
+) Đặt điều kiện để phương trình có nghĩa.
+) Sử dụng các công thức:
(giả sử các biểu thức là có nghĩa).
Cách giải
Điều kiện: x > 0.
Ta có:
![]()
![]()
![]()
![]()
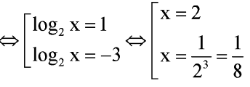
Vậy nghiệm bé nhất của phương trình là
Chọn A.
Câu 23:
Cho số thực a dương khác 1. Biết rằng bất kỳ đường thẳng nào song song với trục Ox mà cắt đường thẳng , trục tung lần lượt tại M, N và A thì AN = 2AM. Giá trị của a bằng
Phương pháp:
+) Gọi theo
+) Tính.Giải phương trình tìm a.
Cách giải:
Ta có
Chọn A.
Câu 24:
Giả sử p, q là các số thực dương thỏa mãn . Tìm giá trị của p/q
Phương pháp
+) Đặt , rút p, q, p + q theo t.
+) Thế p, q theo t vào biểu thức p + q. Chia cả 2 vế cho , đưa phương trình về dạng phương trình bậc hai đối với hàm số mũ.
+) Giải phương trình, từ đó suy ra
Cách giải
Đặt
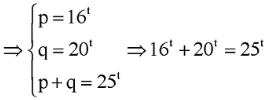
![]()
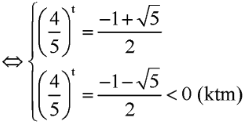
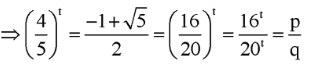
Chọn A.
Câu 25:
Cho . Khi đó, đạo hàm của hàm số là
Chọn đáp án B
Phương pháp
Sử dụng công thức: .
Sử dụng công thức đạo hàm cơ bản: .
Cách giải
Ta có: .
Câu 26:
Với a, b, c là các số thực dương tùy ý khác 1 và . Khi đó giá trị của là
Chọn đáp án A
Phương pháp
Sử dụng công thức: (giả sử các biểu thức có nghĩa).
Cách giải
Ta có: .
Câu 27:
Xác định số thực x để dãy số log 2, log 7, log x theo thứ tự đó lập thành một cấp số cộng.
Chọn đáp án B
Phương pháp
Cho ba số a, b, c lập thành CSC thì ta có: .
Cách giải
Điều kiện .
Ta có 3 số: theo thứ tự thành CSC
.
Câu 28:
Số nghiệm thực của phương trình là
Chọn đáp án C
Phương pháp
Giải phương trình logarit:
Cách giải
ĐKXĐ: .
Câu 29:
Số nghiệm thực của phương trình là
Chọn đáp án A
Phương pháp
Giải phương trình mũ: .
Cách giải
Ta có:
.
Vậy phương trình đã cho có 1 nghiệm.
Câu 30:
Số nghiệm của bất phương trình là
Chọn đáp án B
Phương pháp
+ Giải bất phương trình
Cách giải
ĐKXĐ: .
(Do )
.
Kết hợp điều kiện Bất phương trình vô nghiệm
Vậy bất phương trình có vô số nghiệm thỏa mãn bài toán.
Câu 31:
Gọi S là tập hợp các giá trị thực của tham số m để phương trình có nghiệm. Tập có bao nhiêu giá trị nguyên?
Chọn đáp án C
Phương pháp
+) Đặt , đưa phương trình trở thành phương trình bậc hai ẩn t.
+) Cô lập m, đưa phương trình về dạng . Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng song song với trục hoành.
+) Lập BBT hàm số và kết luận.
Cách giải
Đặt , khi đó phương trình trở thành
Nhận thấy không là nghiệm của phương trình .
Chia cả 2 vế của phương trình cho , ta được
(*)
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng song song với trục hoành.
Ta có:
ta thấy phương trình (*) có nghiệm
có 9 giá trị nguyên là .
Câu 32:
Tập hợp tất cả các số thực x không thỏa mãn bất phương trình là khoảng (a;b). Tính b-a.
Chọn đáp án D
Phương pháp
Xét hai trường hợp và .
Cách giải
TH1: , khi đó ta có:
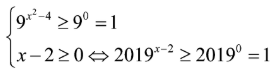
![]()
Dấu “=” xảy ra .
TH2: , khi đó ta có:
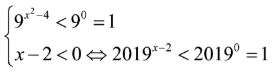
![]()
bất phương trình vô nghiệm.
Vậy tập hợp tất cả các số thực x không thỏa mãn bất phương trình là
.
Câu 33:
Một người vay ngân hàng số tiền 50 triệu đồng, mỗi tháng trả ngân hàng số tiền 4 triệu đồng và phải trả lãi suất cho số tiền còn nợ là 1,1% một tháng theo hình thức lãi kép. Giả sử sau n tháng người đó trả hết nợ. Khi đó n gần với số nào dưới đây?
Chọn đáp án D
Phương pháp
Sử dụng công thức trả góp , trong đó:
P: Số tiền phải trả sau n tháng.
r: lãi suất/ tháng
M: Số tiền trả mỗi tháng.
Cách giải
Câu 34:
Số nghiệm của phương trình là:
Chọn đáp án D
Phương pháp
Sử dụng các công thức , () để đưa phương trình về dạng phương trình logarit cơ bản.
Cách giải
ĐKXĐ:
![]()
![]()
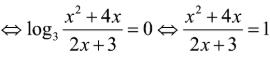
![]()
Vậy phương trình đã cho có duy nhất 1 nghiệm.
Chú ý: Lưu ý ĐKXĐ của phương trình.
Câu 35:
Có bao nhiêu giá trị nguyên của tham số để bất phương trình sau nghiệm đúng ?
Chọn đáp án C
Phương pháp
+) Chia cả 2 vế của bất phương trình cho .
+) Đặt .
+) Đưa bất phương trình về dạng
.
+) Lập BBT hàm số và kết luận.
Cách giải
Chia cả 2 vế của bất phương trình cho ta được:
Nhận xét: , do đó khi ta đặt
.
Phương trình trở thành:
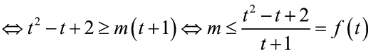 .
.
![]()
Xét hàm số ta có:
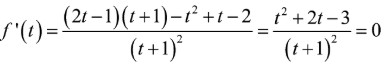
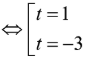
Từ BBT .
Kết hợp điều kiện đề bài
có 12 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 36:
Năm nay con ông Mạnh vào lớp 10. Để chuẩn bị tiền cho con đi học đại học mỗi tháng ông gửi ngân hàng 1000000 với lãi suất 0,7% /tháng. Sau ba năm thì số tiền Ông Mạnh nhận được cả gốc lẫn lãi sau khi ngân hàng đã tính lãi tháng cuối cùng là bao nhiêu?
Chọn A
Gọi số tiền mà Ông Mạnh gửi vào hàng tháng là
Và lãi suất hàng tháng của ngân hàng là
Theo giả thiết:
Sau tháng thứ nhất Ông Mạnh có số tiền là:
Sau tháng thứ hai Ông Mạnh có số tiền là:
![]()
![]()
Sau tháng thứ ba Ông Mạnh có số tiền là:
![]()
![]()
…..
Sau tháng thứ 36 Ông Mạnh có số tiền cả gốc lẫn lãi là
Thay và ta được
Câu 38:
Bác An có mảnh ruộng hình Elip có độ dài trục lớn bằng 100m, độ dài trục bé bằng 80m. Với chủ trương xây dựng kinh tế nông thôn mới, bác định chuyển đổi canh tác bằng cách đào một cái ao hình Elip ở chính giữa vườn có trục lớn bằng 90m trục bé bằng 70m để nuôi tôm, cá. Phần đất còn lại bác làm bờ trồng cây xung quanh. Biết chi phí đào ao hết 250000 đồng và chi phí làm bờ trồng cây là 100000đồng/1m2. Hỏi số tiền bác phải chi gần với số nào nhất.
Chọn A
Chọn hệ trục tọa độ như hình vẽ
Phương trình của Elip của mảnh ruộng là Khi đó mảnh ruộng có diện tích là
Phương trình của Elip của cái ao là Khi đó cái ao có diện tích là
Suy ra diện tích phần bờ trồng cây xung quanh
Chi phí đào ao là đồng.
Chi phí trồng cây xung quanh là đồng
Số tiền bác An phải chi là đồng.
Câu 43:
Ông Bình mua một chiếc xe máy với giá 60 triệu đồng tại một cửa hàng theo hình thức trả góp với lãi suất 8% một năm. Biết rằng lãi suất được chia đều cho 12 tháng và không thay đổi trong suốt thời gian ông Bình trả nợ. Theo quy định của cửa hàng, mỗi tháng ông Bình phải trả một số tiền cố định là 2 triệu đồng (bao gồm tiền nợ gốc và tiền lãi). Hỏi ông Bình trả hết nợ ít nhất là trong bao nhiêu tháng?
Đáp án C
Câu 44:
Cho a,b là các số thực dương thỏa mãn Khẳng định nào sau đây sai?
Đáp án D.
Ta có:
![]()
![]()
phương án D
Câu 45:
Cho đồ thị của hàm số và như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
Đáp án A.
+) Từ điều kiện của hàm số mũ và hàm số logarit suy ra
+) Dựa vào đồ thị suy ra
Vậy
Câu 46:
Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất 0,7%/tháng với tổng số tiền vay của cả ba người là 1 tỉ đồng. Biết rằng mỗi tháng cả ba người đều trả cho ngân hàng một số tiền như nhau để trừ vào tiền gốc và lãi. Để trả hết gốc và lãi cho ngân hàng thì An cần 10 tháng, Bình cần 15 tháng và Cường cần 25 tháng. Số tiền trả đều đặn cho ngân hàng mỗi tháng của mỗi người gần nhất với số tiền nào dưới đây?
Đáp án C.
