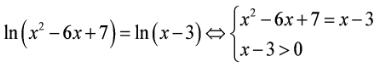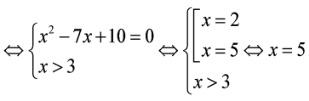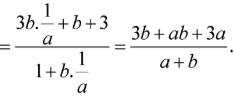256 Bài tập Hàm số mũ và Logarit cực hay có lời giải chi tiết (P4)
-
4774 lượt thi
-
50 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Tổng tất cả các nghiệm của phương trình bằng:
Chọn đáp án B.
Phương pháp
+) Giải phương trình logarit cơ bản: .
+) Giải phương trình bậc cao đối với hàm số mũ.
Cách giải
Vậy tập nghiệm của phương trình là .
Câu 2:
Tập nghiệm S của bất phương trình là:
Chọn đáp án D.
Phương pháp
Giải bất phương trình mũ cơ bản: .
Cách giải
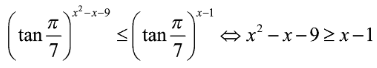
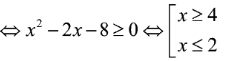
Vậy tập nghiệm của bất phương trình là
Câu 3:
Cho . Tính giá trị của biểu thức
Chọn đáp án C.
Phương pháp
Sử dụng các công thức:
![]()
![]()
Cách giải
![]() .
.
![]()
![]()
Câu 6:
Trong các hàm số sau đây, hàm số nào đồng biến trên R
Chọn A.
Phương pháp:
Hàm số
+) Nếu thì hàm số đồng biến trên R.
+) Nếu thì hàm số nghịch biến trên R.
Cách giải:
Ta có: Hàm số đồng biến trên R.
Câu 7:
Tập nghiệm S của bất phương trình là
Chọn C.
Phương pháp:
Cách giải:
Ta có: 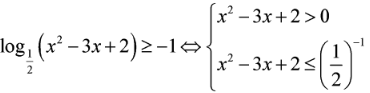
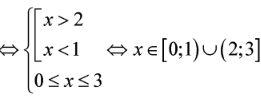
Tập nghiệm của bất phương trình là
Chú ý: HS cần chú ý ĐKXĐ của hàm logarit
Câu 8:
Cho Khi đó log60 bằng
Chọn B.
Phương pháp:
(các biểu thức trên đều xác định)
Cách giải:
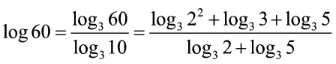
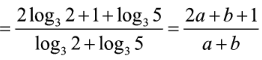
Câu 9:
Số nghiệm của phương trình -7=0 là
Chọn C.
Phương pháp:
Cách giải:
ĐKXĐ:
Ta có:
![]()
![]()
Phương trình đã cho có 2 nghiệm
Câu 10:
Tính tổng T của các giá trị nguyên của tham số m để phương trình có đúng hai nghiệm phân biệt nhỏ hơn
Chọn D.
Phương pháp:
+) Đặt đưa phương trình về phương trình bậc hai ẩn t.
+) Tìm điều kiện của ẩn t, sử dụng định lí Vi-ét.
Cách giải:
Đặt phương trình trở thành (*).
Ta có
Bài toán trở thành tìm điều kiện để phương trình (*) có 2 nghiệm thỏa mãn
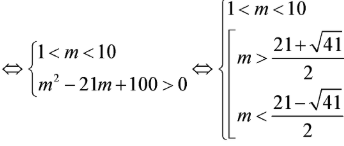
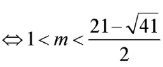
Kết hợp điều kiện
Vậy tổng các phần tử của T bằng 27.
Câu 11:
Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực R?
Chọn C.
Phương pháp:
Hàm số nghịch biến trên và bằng 0 tại hữu hạn điểm.
Cách giải:
+) Đáp án A: TXĐ: D = R.
Ta có: là hàm đồng biến trên loại đáp án A.
+) Đáp án B: TXĐ: D = R.
Ta có: hàm số có sự đổi dấu qua điểm loại đáp án B.
+) Đáp án C: TXĐ: D = R.
Ta có: là hàm nghịch biến trên chọn đáp án C.
Câu 12:
Tìm tập nghiệm S của bất phương trình
Chọn C.
Phương pháp
Giải bất phương trình
Cách giải:
Câu 13:
Gọi T là tổng các nghiệm của phương trình Tính T.
Chọn C.
Phương pháp:
Sử dụng công thức đưa phương trình về dạng phương trình bậc hai của
hàm số logarit.
Cách giải:
ĐK:
![]()
![]()
![]()
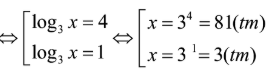
Câu 15:
Với giá trị nào của x thì biểu thức sau có nghĩa
Chọn C.
Phương pháp:
Xét hàm số :
+ Nếu là số nguyên dương thì TXĐ:
+ Nếu là số nguyên âm hoặc bằng 0 thì TXĐ:
+ Nếu là không phải là số nguyên thì TXĐ:
Cách giải:
ĐKXĐ:
Câu 16:
Đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Chọn B
Phương pháp:
đồng biến trên với và nghịch biến trên với
Cách giải:
Hàm số đồng biến trên Loại phương án C.
Đồ thị hàm số đi qua điểm Chọn phương án B, do và
Câu 17:
Hỏi có bao nhiêu giá trị m nguyên trong để phương trình nghiệm duy nhất?
Chọn D.
Phương pháp:
Đánh giá số nghiệm của phương trình bậc hai.
Cách giải:
Ta thấy không phải nghiệm khi đó
Xét hàm số có
Dựa vào bảng biên thiên, ta có: phương trình đã cho có 1 nghiệm duy nhất
Mà
Có 2018 giá trị của m thỏa mãn
Câu 18:
Tích được viết dưới dạng khi đó (a;b) là cặp nào trong các cặp sau
Chọn C.
Phương pháp:
Sử dụng công thức nhân hai lũy thừa cùng cơ số
Cách giải:
Khi đó là
Câu 19:
Cho Khi đó giá trị của x là
Chọn A.
Phương pháp:
Sử dụng công thức
Cách giải:
Ta có:
Câu 21:
Đầu năm 2016, Curtis Cooper và các cộng sự tại nhóm nghiên cứu Đại học Central Mis-souri, Mỹ công bố số nguyên tố lớn nhất tại thời điểm đó. Số nguyên tố này là một dạng Mersenne, có giá trị bằng Hỏi M có bao nhiêu chữ số?
Chọn D.
Phương pháp:
Nếu thì số M có n + 1 chữ số
Cách giải:
+) Xác định số chữ số của
Tìm số tự nhiên n thỏa mãn

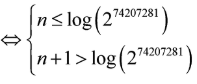
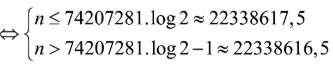
![]()
Vậy có n + 1 = 22338618 chữ số
+) Xác định số chữ số của
Nhận xét: Do M + 1 là số có 22338618 chữ số nên M hoặc có 22338618 chữ số hoặc có 22338617 chữ số.
M có 22338617 khi và chỉ khi
tức là
vô lý do 2 là số chẵn và 5 là số lẻ
Vậy là số có 22338167 chữ số
Câu 22:
Tổng các nghiệm của phương trình là:
Chọn D.
Phương pháp
Sử dụng phương pháp đưa về cùng cơ số
Sử dụng các công thức với
Cách giải:
ĐK:
Ta có
![]()
![]()
(thỏa mãn)
Tổng các nghiệm của phương trình là 6 + (-6) = 0.
Chú ý:
Câu 23:
Tập nghiệm của phương trình là:
Chọn D.
Phương pháp
Sử dụng
Cách giải:
ĐK:
Ta có
![]()
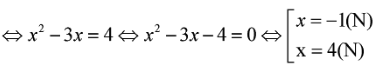
Vậy tập nghiệm của bất phương trình là S = {-1;4}.
Câu 24:
Phương trình có bao nhiêu nghiệm âm?
Chọn B.
Phương pháp
Chuyển vế, chia cả hai vế cho và giải phương trình thu được tìm nghiệm.
Cách giải:
Đặt thì
Vậy phương trình không có nghiệm nào âm.
Câu 25:
Cho các số thực a, b thỏa mãn 0 < a < 1 < b. Tìm khẳng định đúng:
Chọn A.
Phương pháp
Xét tính đúng sai của từng đáp án dựa vào điểu kiện của a, b.
Cách giải:
Đáp án A: (vì 0 < a < 1 và b > 1) nên A đúng.
Đáp án B: vì a < b nên B sai.
Đáp án C: Vì 0 < 0,5 < 1 và a < b nên nên C sai.
Đáp án D: Vì 2 > 1 và a < b nên nên D sai.
Câu 26:
Cho a, b là hai số thực dương tùy ý và b khác 1 Tìm kết luận đúng.
Chọn D.
Phương pháp:
Sử dụng tính chất của logarit nhận xét tính đúng sai của từng đáp án.
Cách giải:
nên A sai.
nên B sai.
nên C sai.
nên D đúng.
Câu 27:
Tập xác định của hàm số là:
Chọn B.
Phương pháp:
Hàm số xác định nếu xác định và
Cách giải:
Hàm số xác định nếu
Vậy TXĐ
Chú ý khi giải: Nhiều em biến đổi rồi chọn C là sai.
Câu 28:
Tìm đạo hàm của hàm số
Chọn D.
Phương pháp:
Sử dụng công thức đạo hàm và
Cách giải:
Ta có
Câu 29:
Anh Bình gửi 200 triệu đồng vào ngân hàng VB với kì hạn cố định 12 tháng và hưởng mức lãi suất là 0,65%/tháng. Tuy nhiên, sau khi gửi được tròn 8 tháng anh Bình có việc phải dùng đến 200 triệu trên. Anh đến ngân hàng đình rút tiền thì được nhân viên ngân hàng tư vấn: “Nếu rút tiền trước hạn, toàn bộ số tiền anh gửi chỉ được hưởng mức lãi suất không kì hạn là 0,02%/tháng. Anh nên thế chấp sổ tiết kiệm đó tại ngân hàng để vay ngân hàng 200 triệu với lãi suất 0,7%/tháng. Khi sổ của anh đến hạn, anh có thể rút tiền để trả nợ ngân hàng”. Nếu làm theo tư vấn của nhân viên ngân hàng, anh Bình sẽ đỡ thiệt một số tiền gần nhất với con số nào dưới đây (biết rằng ngân hàng tính lãi theo thể thức lãi kép)?
Chọn D.
Phương pháp:
Sử dụng công thức lãi kép: với A0 là số tiền gốc ban đầu, r là lãi suất, A là tổng tiền cả gốc và lãi thu được sau n kì hạn.
Cách giải:
* Nếu anh Bình nghe theo nhân viên tư vấn ngân hàng
+ Tiền lãi sanh Bình nhận được sau khi gửi 200 triệu trong 12 tháng với mức lãi suất 0,65%/ tháng là (triệu đồng)
+ Tiền lãi anh Bình phải trả khi vay nợ 200 triệu đồng với lãi suất 0,7%/ tháng là (triệu đồng)
Tổng số tiền lãi anh Bình nhận được là M = A – B
* Nếu anh Bình rút tiền ngay
Số tiền lãi anh Bình nhận được trong 8 tháng với mức lãi suất 0,02%/ tháng là
Suy ra nếu làm theo nhân viên tư vấn ngân hàng thì anh Bình sẽ đỡ thiệt số tiền là triệu đồng.
Câu 30:
Số nghiệm của phương trình là:
Chọn C.
Phương pháp:
Phương trình
Cách giải:
Ta có:
Phương trình đã cho có 2 nghiệm phân biệt.
Câu 31:
Cho đa giác đều n đỉnh, và n > 3. Tìm n biết rằng đa giác đã cho có 135 đường chéo.
Chọn C.
Phương pháp:
Số đường chéo của đa giác có n đỉnh là:
Cách giải:
Theo đề bài ta có:
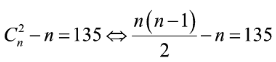
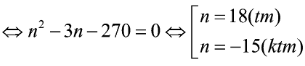
Vậy n = 18.
Câu 32:
Tập xác định của hàm số là tập hợp nào sau đây?
Chọn A.
Phương pháp:
TXĐ của hàm số là
Cách giải:
ĐKXĐ:
TXĐ: D = (-2;2).
Câu 33:
Tập nghiệm của bất phương trình là:
Chọn B.
Phương pháp:
Với
Với
Cách giải:
Ta có: 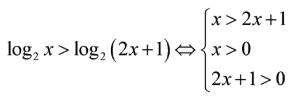
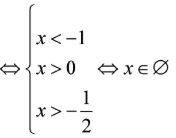
Vậy, tập nghiệm của bất phương trình là:
Câu 34:
Cho a, b, c > 1. Biết rằng biểu thức đạt giá trị nhỏ nhất bằng m khi Tính giá trị m + n.
Chọn C.
Phương pháp:
Áp dụng BĐT Cô-si cho 2 số dương:
Cách giải:
Do a, b, c > 1 nên
![]()
![]()
![]()
![]()

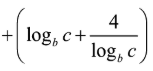
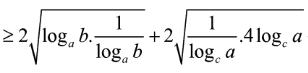
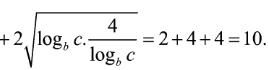
Dấu “=” xảy ra khi và chỉ khi
Vậy, đạt giá trị nhỏ nhất là 10 khi
Câu 35:
Một sinh viên A mua máy tính xách tay theo hình thức trả góp với giá tiền 20 triệu đồng, mức lãi suất 1,2%/tháng trong năm đầu tiên, mỗi tháng anh A phải trả 800 ngàn đồng, cả gốc và lãi. Sau một năm lãi suất tăng lên là 1,5%/tháng và anh A phải trả 1 triệu đồng cả gốc và lãi mỗi tháng (trừ tháng cuối). Hỏi sau tối đa bao nhiêu tháng anh A trả hết nợ (tháng cuối trả không quá 500 ngàn đồng)
Chọn D.
Phương pháp:
Giả sử anh A nợ ngân hàng M ngàn đồng), mỗi tháng anh A gửi vào ngân hàng a ngàn đồng, lãi suất ngân hàng là r (%). Số tiền anh A còn nợ ngân hàng :
+ Sau tháng thứ 1 là:
+ Sau tháng thứ 2 là:
+ Sau tháng thứ 3 là:
![]()
![]()
+ sau tháng thứ 4 là:
![]()
![]()
…….
+ Sau tháng thứ n là:
![]()
![]()
Cách giải:
Số tiền sinh viên A còn nợ sau 1 năm đầu là:
(nghìn đồng)
Gọi n là số tháng (tính từ năm thứ hai) mà sinh viên A trả được hết nợ, ta có:
Vậy, số tháng để sinh viên A trả hết nợ là: 12 + 15 = 27 (tháng)
Câu 39:
Tập nghiệm của bất phương trình là
Chọn A.
Lời giải:
Ta có:

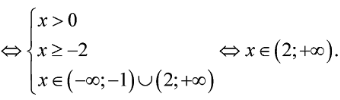
Vậy bất phương trình có tập nghiệm là
Câu 40:
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình có nghiệm thuộc khoảng (0;ln3):
Chọn D.
Lời giải:
Đặt ẩn phụ: phương trình trở thành với .
YCBT có nghiệm có nghiệm
Dựa vào đồ thị hàm số ở hình trên, ta có:
Câu 41:
Cho hàm số y=f(x) Hàm số y=f'(x) có bảng biến thiên như hình vẽ:

Bất phương trình có nghiệm khi và chỉ khi
Chọn C.
Lời giải:
Ta có
Xét
Có
(vì
)
Hàm số đồng biến trên
Bất phương trình (1) có nghiệm thuộc .
Câu 42:
Anh Việt vay tiền ngân hàng 500 triệu đồng mua nhà và trả góp hàng tháng. Cuối mỗi tháng bắt đầu từ tháng thứ nhất anh trả 10 triệu đồng và chịu lãi suất là 0,9%/tháng cho số tiền chưa trả. Với hình thức hoàn nợ như vậy thì sau bao lâu anh Việt sẽ trả hết số nợ ngân hàng?
Chọn B.
Lời giải:
Gọi rlà lãi suất của khoản vay.
- Số nợ của Việt sau tháng thứ nhất là:
(triệu đồng)
- Số nợ của Việt sau tháng thứ hai là:
![]()
![]() (triệu đồng)
(triệu đồng)
…
- Số nợ của Việt sau tháng thứ là:
(triệu đồng)
Giả sử sau tháng thứ , Việt trả được hết số nợ, khi đó
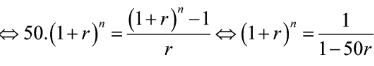
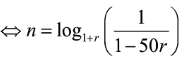
Vậy
Tức là sau khoảng 67 tháng Việt trả hết được số nợ ngân hàng.
Câu 44:
Tập nghiệm S của bất phương trình là:
Phương pháp:
Cách giải:
Ta có:
Tập nghiệm S của bất phương trình là:
Chọn D.
Câu 46:
Ông T vay Ngân hàng nông nghiệp tỉnh Lào Cai một tỷ đồng theo phương thức trả góp để làm vốn kinh doanh. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất ông T trả 40 triệu đồng và chịu lãi số tiền chưa trả là 0,65% mỗi tháng (biết lãi suất không thay đổi) thì sao bao nhiêu tháng ông T trả hết số tiền trên?
Phương pháp:
Dành cho bài toán trả góp: Gọi số tiền vay là N, lãi suất là r, n là số tháng phải trả, A là số tiền phải trả vào tháng để sau n tháng là hết nợ:
Cách giải:
Ta có:
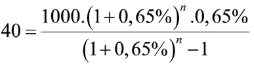
![]()
Vậy, sau 28 tháng, ông T trả hết số tiền trên.
Chọn B.
Câu 47:
Tập xác định của hàm số là
Chọn C
Hàm số xác định khi Tập xác định của hàm số là .
Câu 48:
Phương trình có bao nhiêu nghiệm?
Chọn C
Điều kiện: .
.![]()

Đối chiếu điều kiện ta thấy thỏa mãn. Vậy phương trình có một nghiệm
.
Câu 49:
Cho m, n, p là các số thực thỏa mãn p log2=mlog4+n log8, mệnh đề nào dưới đây đúng?
Chọn C
.
Câu 50:
Đường cong ở hình vẽ bên dưới là đồ thị của hàm số nào dưới đây?
Chọn C
Quan sát đồ thị ta thấy đồ thị hàm số đi qua điểm cố định và là hàm số nghịch biến. Do đó ta loại đáp án A, B.
Mặt khác, hàm số có tập xác định là nên ta chọn đáp án C.