30 câu hỏi trắc nghiệm thuộc 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P3)

Câu 1:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sqrt{- x^{2} + 6 x - 5}$ trên đoạn [1;5] lần lượt là

A. 2 và 0

B. 4 và 0

C. 3 và 0

D. 0 và -2

Xem đáp án

Đáp án A.

Vì y(1) = y(5) = 0 và y(3) = 2 nên giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [1;5] lần lượt là 2 và 0

Câu 2:

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = 2 x - 4 \sqrt{6 - x}$ trên đoạn [-3;6]. Tổng M + m có giá trị là

A. 18

B. -6

C. -12

D. -4

Xem đáp án

Đáp án B

Câu 3:

Hàm số $y = \sqrt{4 - x} - \sqrt{x + 6}$ đạt giá trị nhỏ nhất tại x = x₀. Tìm x₀

A. x₀ = -6

B. x₀ = -1

C. x₀= 0

D. x₀ = 4

Xem đáp án

Đáp án D

Điểu kiện

Xét -6 < x < 4, khi đó áp dụng công thức ta có:

=> hàm số đã cho nghịch biến trên -6 ≤ x ≤ 4

Vì vậy, hàm số đạt giá trị nhỏ nhất tại x₀ = 4

Câu 4:

Hàm số $y = 4 \sqrt{x^{2} - 2 x + 3} + 2 x - x^{2}$ đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là

A. 2

B. 1

C. 0.

D. -1

Xem đáp án

Đáp án D.

Câu 5:

Giá trị nhỏ nhất của hàm số $y = \sqrt{6 - x} - \sqrt{x + 4}$ đạt tại x₀, tìm x₀?

A. x₀ = -√10

B. x₀ = -4

C. x₀ = 6

D. x₀ = √10

Xem đáp án

Đáp án B

Câu 6:

Cho hàm số $y = 5 \sqrt{3 - x}$ Tìm giá trị nhỏ nhất của hàm số.

A. 3

B. 5

C. 0

D. 1

Xem đáp án

Đáp án C.

TXD: x ≤ 3. Xét hàm số liên tục $y = 5 \sqrt{3 - x}$ trên (-∞;3] ta có:

Từ đó suy ra giá trị nhỏ nhất của hàm số là Min y = f(3) = 0.

Câu 7:

Tìm giá trị m để hai đường tiệm cận của đồ thị hàm số $y = \frac{m x + 2}{3 - 2 x}$ ( m khác $- \frac{4}{3}$ )tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 1/5

A. m = ±4/15.

B. m = ±15/4

C. m = 14/5

D. m = -14/5

Xem đáp án

Đáp án A

Câu 8:

Cho hàm số y = ax⁴ + bx² + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

A. a > 0, b< 0, c > 0

B. a < 0, b > 0, c < 0

C. a < 0, b< 0, c < 0

D. a > 0, b< 0, c < 0

Xem đáp án

Đáp án B.

Nhánh ngoài cùng bên phải của hàm số bậc bốn trùng phương đi xuống nên a < 0.

Đồ thị hàm số bậc bốn trùng phương có ba cực trị nên a.b < 0 => b > 0

Do đồ thị cắt trục Oy tại điểm có tung độ âm nên c < 0

Câu 9:

Tìm m để hàm số y = x⁴ – 2mx² + 2m + m⁴ – 5 đạt cực tiểu tại x = -1

A. m = -1

B. m ≠ 1

C. m = 1

D. m ≠ -1

Xem đáp án

Đáp án C.

Ta có y’ = 4x³ – 4mx; y’’ = 12x² – 4m.

Để hàm số đạt cực tiểu tại x = -1 thì y’(-1) = 0 ó -4 + 4m = 0 ó m = 1

Khi m = 1 thì y’’(-1) = 12 – 4m = 12 – 4.1 = 8 > 0 => hàm số đạt cực tiểu tại x = -1.

Vậy m = 1 là giá trị cần tìm

Câu 10:

Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên

A. y = x³ + 3x + 1

B. y = x³ – 3x + 1

C. y = -x³ – 3x + 1

D. y = -x³ + 3x + 1

Xem đáp án

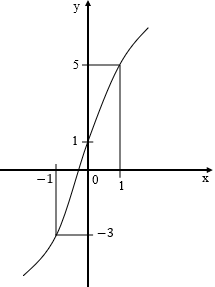
Đáp án A.

Nhánh ngoài cùng bên phải của hàm số bậc ba y = ax³ + bx² + cx + d đi lên nên a > 0.

Hàm số không có cực trị nên y’ ≥ 0, với mọi x

Hàm số cần tìm là y = x³ + 3x + 1

Câu 11:

Cho hàm số y = f(x) xác định và liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực đại tại điểm nào dưới đây?

A. x = - 2

B. x = 0

C. x = 1

D. x = 2

Xem đáp án

Câu 12:

Đường cong trong hình bên là đồ thị của hàm số nào sau đây?

A. y = x⁴ – 2x² – 3

B. y = x⁴ + 8x² – 9

C. y = -x⁴ + 2x² – 3

D. y = x⁴ + 2x² – 3

Xem đáp án

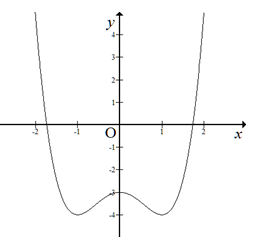
Đáp án A.

Hàm số cắt trục tung tại (0;-3) suy ra c = -3

Dựa vào đồ thị hàm số suy ra a > 0 và b < 0 (y’ = 0 có 3 nghiệm phân biệt)

Câu 13:

Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = -x³ – 4

B. y = x³ – 3x² – 4

C. y = -x³ + 3x² – 4

D. y = -x³ + 3x² – 2.

Xem đáp án

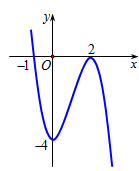
Đáp án C.

Hàm số cắt trục tung tại (0;-4) suy ra c = -4

Dựa vào đồ thị hàm số suy ra a < 0 và y’ = 0 có 2 nghiệm phân biệt

Câu 14:

Cho hàm số y = -x³ + 6x² – 4. Mệnh đề nào dưới đây sai?

A. Hàm số đạt cực trị tại x = 0

B. Hàm số nghịch biến trên khoảng (-∞;1)

C. Hàm số đồng biến trên khoảng (0;4)

D. Đồ thị hàm số có 2 điểm cực trị

Xem đáp án

Đáp án B

Ta có y’ = -3x² + 12x; y’ = 0

Bảng biến thiên

Câu 15:

Bảng biến thiên sau đây là của hàm số nào?

A. y = x⁴ – 3x² – 3

B. y = -x⁴ + 2x² – 3

C. y = x⁴ + 2x² – 3

D. y =x⁴ – 2x² – 3

Xem đáp án

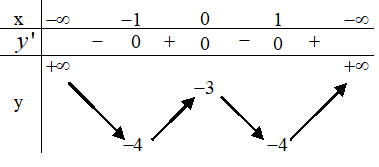
Đáp án D.

Nhìn vào bảng biến thiến ta có

a > 0 và y’ = 0 có 3 nghiệm x = 0; x = ±1

Câu 16:

Bảng biến thiên sau đây là của hàm số nào?

A.

B.

C.

D.

Xem đáp án

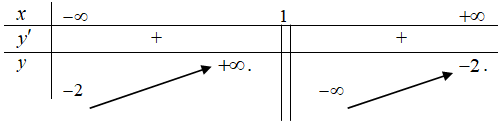
Đáp án C.

Hàm số trong BBT có tiệm cận đứng và tiệm cận ngang lần lượt là x = 1 và y = -2, vì vậy loại được phương án A.

Đồng thời hàm số đồng biến trên các khoảng xác định, nên Đáp án C

Câu 17:

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = -x⁴ – 2x²

B. y = x⁴ – 2x²

C. y = x⁴ + 2x²

D. y = -x⁴ + 2x²

Xem đáp án

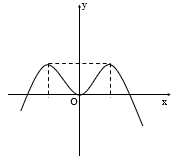
Đáp án D.

Từ hình dạng đồ thị y = ax⁴ + bx² + c (a ≠ 0) ở trên, ta thấy: a < 0 và đồ thị có ba cực trị nên a.b < 0 => b > 0. Do đó Đáp án D

Câu 18:

Hình ảnh bên là đồ thị của hàm số nào sau đây?

A. y = x⁴ – 2x² – 3

B. y = x⁴ + 2x² – 3

C. y = -x⁴ + 2x² + 3

D. y = -x⁴ – 2x² + 3

Xem đáp án

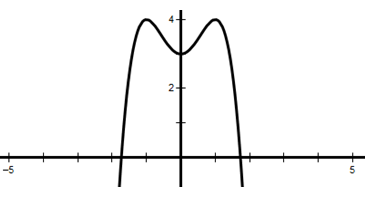
Đáp án C.

Loại câu A và B vì a = 1 > 0

Đồ thị hàm số đi qua điểm (1;4) thay vào đáp án C và D ta thấy đáp án C thỏa mãn.

Câu 19:

Đồ thị hình bên là của hàm số nào? Chọn một khẳng định ĐÚNG

A.

B.

C.

D.

Xem đáp án

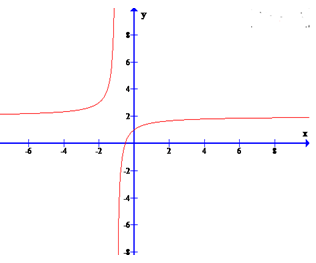
Đáp án D.

Hai tiệm cận là x = -1; y = 2

Câu 20:

Bảng biến thiên sau là của hàm số nào?

A. y = x⁴ – 2x² + 1

B. y = x⁴ – 2x² – 1

C. y = x⁴ – x² – 1

D. y = -x⁴ + 2x² – 1

Xem đáp án

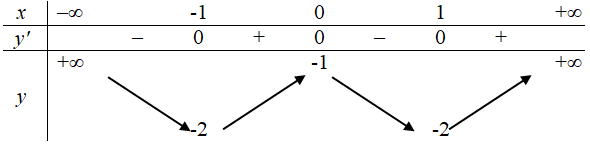
Đáp án B.

y = x⁴ – 2x² – 1

y’ = 4x³ – 4x; y’ = 0 ó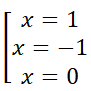

Cực trị của hàm số:

* Hàm số đạt cực tiểu tại hai điểm x = 1 và x = -1; y_CT = y(±1) = -2

* Hàm số đạt cực đại tại điểm x = 0; y_CĐ = y(0) = -1

Tìm hàm số nên được làm khác, VD: a > 0; b, c…..

Câu 21:

Cho biết hàm số y = ax³ + bx² + cx + d có đồ thị như hình vẽ bên. Trong các khẳng định sau, khẳng định nào đúng?

A.

B.

C.

D.

Xem đáp án

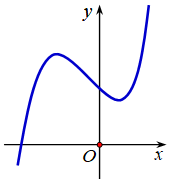
Đáp án D.

Từ đồ thị ta thấy có a > 0 và có 2 cực trị => y’ = 3ax² + 2bx + c = 0 có hai nghiệm phân biệt hay D = 4b² – 12ac > 0 ó b² – 3ac > 0

Câu 22:

Cho hàm số có bảng biến thiên ở hình bên. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số có 2 cực trị

B. Hàm số có giá trị cực đại bằng 3

C. Hàm số có giá trị lớn nhất bằng 3, giá trị nhỏ nhất bằng -1

D. Hàm số đạt cực tiểu tại x = 0

Xem đáp án

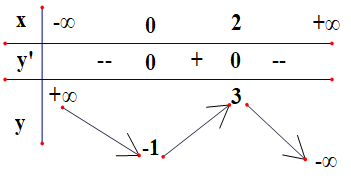
Đáp án C.

Do nên hàm số không xác định được GTLN, GTNN của hàm số

Câu 23:

Đồ thị trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A.

B.

C.

D.

Xem đáp án

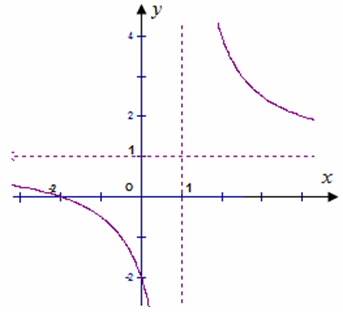
Đáp án C.

Đồ thị có:

+) Tiệm cận đứng: x = 1. Tiệm cận ngang: y = 1 => loại B, D.

+) Giao với trục hoành tại điểm A(-2;0) => loại A;

+) Vậy Đáp án C.

+) Mặt khác đồ thị nằm cung phần tư thứ I, III nên y’ < 0

Câu 24:

Đường cong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là hàm số nào?

A. y = -x³ – 3x + 1

B. y = x² – 6x + 1

C. y = x³ – 6x + 1

D. y = x⁴ – 3x² + 1

Xem đáp án

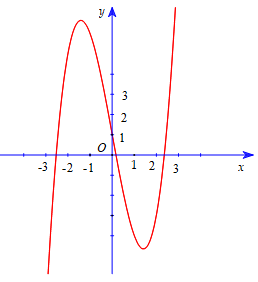
Đáp án C.

Ta thấy nhánh cuối bên phải của đồ thị hướng lên trên nên hệ số a > 0 => loại A.

Đồ thị hàm số có hai điểm cực trị => loại B, D do:

+ Hàm số y = x² – 6x + 1 có 1 điểm cực trị

+ Hàm số y = x⁴ – 3x² + 1 có 3 điểm cực trị

Câu 25:

Đồ thị sau đây là của hàm số nào?

A.

B.

C.

D.

Xem đáp án

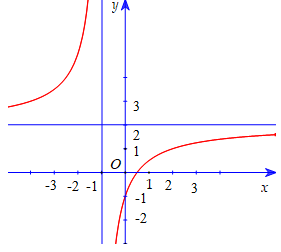
Đáp án D.

Đồ thị hàm số có tiệm cận đứng là x = -1 và tiệm cận ngang là y = 2 => loại đáp án B, C

Đồ thị hàm số đi qua điểm (-1;0) nên chọn D

Câu 26:

Đường cong trong hình là đồ thị của một trong 4 hàm số được cho bởi các phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào

A. y = x⁴ – x² + 1

B. y = x³ – 3x² + 1

C. y = -x³ + 3x² – 1

D. y = x² – 4x + 3

Xem đáp án

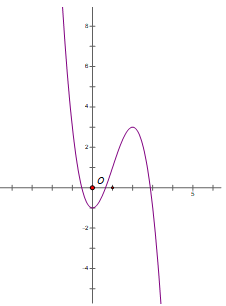
Đáp án C.

Đồ thị trên hình là đồ thị của một hàm số bậc 3 với hệ số a < 0. Do đó chọn đáp án C

Câu 27:

Đồ thị sau đây là của hàm số nào?

A. y = x³ – 3x – 4

B. y = -x³ + 3x² - 4

C. y = x³ – 3x – 4

D. y = -x³ – 3x² - 4

Xem đáp án

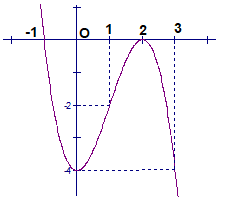
Đáp án B.

Dựa vào đồ thị, ta nhận thấy a < 0 nên loại ngay phương án A, C.

Đồ thị hàm số đi qua điểm (2;0) nên chỉ có phương án B thỏa mãn.

Câu 28:

Tìm các giá trị của tham số m để hàm số y = $\frac{1}{3} x^{3}$ – x² + (m² – 4)x + 11 đạt cực tiểu tại x = 3

A. m = -1

B. m = 1

C. m = {-1;1}

D. m = 0.

Xem đáp án

Đáp án C.

y' = x² – 2x + m² – 4; y'' = 2x - 2

Để hàm số đạt cực tiểu tại x = 3

ó $\{\begin{cases} y ’ (3) = 0 \\ y'' (3) > 0 \end{cases}$ ó $\{\begin{cases} m^{2} - 1 = 0 \\ 2.3 - 2 > 0 \end{cases}$ ó m = ±1

Câu 29:

Cho hàm số $y = \frac{a x + b}{c x + d}$ với a > 0 có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

A. b > 0, c < 0, d < 0.

B. b > 0, c > 0, d < 0

C. b < 0, c > 0, d < 0

D. b < 0, c < 0, d < 0

Xem đáp án

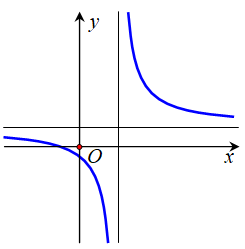
Đáp án B.

Từ đồ thị ta có:

Loại b > 0, c < 0, d < 0 và b < 0, c < 0, d < 0. Còn lại b > 0, c > 0, d < 0; b <0, c > 0, d < 0.

* Cho x = 0 => y = b/d < 0 => b > 0. Đáp án B > 0, c > 0, d < 0.

Câu 30:

Đồ thị (C) của hàm số $y = \frac{2 x - 8}{x}$ cắt đường thẳng Δ: y = -x tại hai điểm phân biệt A và B. Tìm tọa độ trung điểm I của đoạn thẳng AB

A. I(-1;1).

B. I(-2;2).

C. I(3;-3).

D. I(6;-6).

Xem đáp án

Đáp án A

Phương trình hoành độ giao điểm của (C) và $∆$ có dạng:

$\frac{2 x - 8}{x} = - x$ (x ≠ 0).

Gọi I(x₁;y₁) là trung điểm đoạn thẳng AB.

CHỌN BỘ SÁCH BẠN MUỐN XEM

250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số

250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương